Radius of Curvature
1.वक्रता त्रिज्या (Radius of Curvature)-
- वक्रता त्रिज्या (Radius of Curvature),वक्रता वृत्त की त्रिज्या को कहते हैं।
- वक्रता त्रिज्या की परिभाषा (Radius of Curvature Definition)-
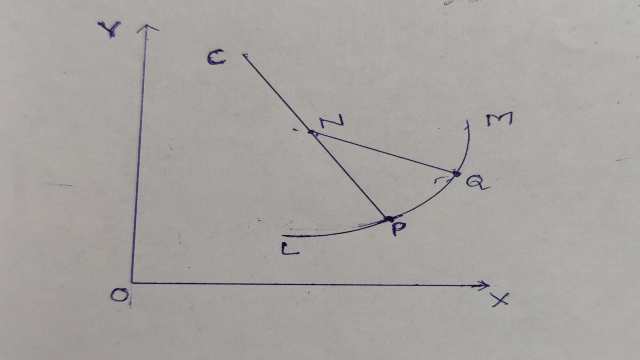
माना LM एक दिया हुआ वक्र है तथा इस पर एक बिन्दु P है,साथ ही वक्र पर Q एक अन्य बिन्दु है।अब P तथा Q पर अभिलम्ब खींचे।माना यह दोनों अभिलम्ब N पर मिलते हैं।अब बिन्दु Q को ,बिन्दु P की ओर वक्र पर प्रवृत्त (approach) करते हैं। जैसे-जैसे बिन्दु Q ,बिन्दु P के समीप पहुंचेगा, वैसे-वैसे बिन्दु N एक निश्चित बिन्दु C पर प्रवृत्त होगा। - अतः सीमा में बिन्दु N बिन्दु C पर प्रवृत्त होता है। यहां हमने Q बिन्दु वक्र पर लिया है तथा इस पर कोई प्रतिबन्ध नहीं लगाया है कि वह P के दांए है या बाएं।ऐसी स्थिति में बिन्दु C को बिन्दु P पर वक्र का वक्रता केन्द्र (Centre of Curvature) कहते हैं तथा दूरी CP को बिन्दु P पर वक्र की वक्रता त्रिज्या (Radius of Curvature) कहते हैं।
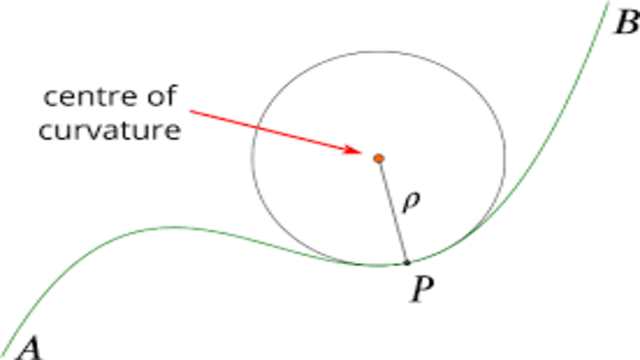
- CP दूरी के व्युत्क्रम (reciprocal), 1/CP को बिन्दु P पर वक्र की वक्रता (Curvature) कहते हैं। आमतौर पर वक्रता त्रिज्या (Radius of Curvature) को ग्रीक अक्षर (Greek Letter ) \rho से निरूपित करते हैं।वह वृत्त जिसका केन्द्र C हो तथा त्रिज्या (Radius) CP हो,को बिन्दु P पर वक्र का वक्रता-वृत्त (Circle of Curvature) कहते हैं तथा बिन्दु P से खींची गई, वक्रता-वृत्त में, कोई जीवा को वक्रता-जीवा (Chord of Curvature) कहते हैं।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Lengths of chords of curvature
2.वक्रता त्रिज्या के लिए कार्तीय सूत्र (Cartesian Formula for Radius of Curvature),वक्रता-त्रिज्या सूत्र (Radius of Curvature Formula),वक्रता त्रिज्या का सूत्र क्या है? (What is the formula of radius of curvature?),वक्रता-त्रिज्या सूत्र का प्रमाण (Radius of Curvature formula proof)-
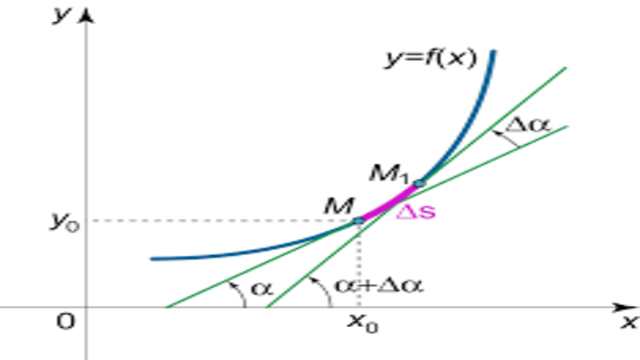
हम जानते हैं कि \frac { dy }{ dx } =\tan { \psi }
दोनों पक्षों का x के सापेक्ष अवकलन करने पर-
\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\sec ^{ 2 }{ \psi } \\ =\sec ^{ 2 }{ \psi } .\frac { d\psi }{ ds } .\frac { ds }{ dx } \\ =[1+{ \left( \frac { dy }{ dx } \right) }^{ 2 }].\frac { 1 }{ \rho } .{ \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 1 }{ 2 } }\\ \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } } \\ \rho =\frac { { \left( 1+{ y }_{ 1 }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { y }_{ 2 } }
जहां { y }_{ 1 }=\frac { dy }{ dx } तथा { y }_{ 2 }=\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } }
वक्रता त्रिज्या (Radius of Curvature) की परिभाषा के अनुसार इसका मान केवल वक्र पर निर्भर करता है न कि अक्षों पर।
अतः x तथा y अक्षों को आपस में परिवर्तित (interchange) करने पर वक्रता त्रिज्या (Radius of Curvature) के लिए हमें निम्न सूत्र प्राप्त होता है।
\rho =\frac { { \left( 1+{ \left( \frac { dx }{ dy } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }x }{ d{ y }^{ 2 } } \right) } }
उपर्युक्त सूत्र तब सर्वोपयोगी होता है जबकि जिस बिन्दु पर वक्रता त्रिज्या (Radius of Curvature) ज्ञात करनी होती है उस पर स्पर्श-रेखा y-अक्ष के समान्तर हो।
3.वक्रता त्रिज्या के हल सहित उदाहरण (Radius of Curvature problems with solutions)-
निम्न वक्रों के बिन्दु (x,y) पर वक्रता-त्रिज्या ज्ञात कीजिए:
(Find the radius of curvature at the point (x,y) on the following curves:)
Example-1.y=c\log { \sec { \left( \frac { x }{ c } \right) } }
Solution–y=c\log { \sec { \left( \frac { x }{ c } \right) } }
x के सापेक्ष अवकलन करने पर-
\frac { dy }{ dx } =c.\frac { 1 }{ \sec { \left( \frac { x }{ c } \right) } } .\sec { \left( \frac { x }{ c } \right) } .\tan { \left( \frac { x }{ c } \right) } .\frac { 1 }{ c } \\ \Rightarrow \frac { dy }{ dx } =\tan { \left( \frac { x }{ c } \right) }
पुनः x के सापेक्ष अवकलन करने पर-
\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\sec ^{ 2 }{ \left( \frac { x }{ c } \right) } .\frac { 1 }{ c } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { 1 }{ c } \sec ^{ 2 }{ \left( \frac { x }{ c } \right) } \\ \Rightarrow \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } } \\ \Rightarrow \rho =\frac { { \left( 1+\tan ^{ 2 }{ \left( \frac { x }{ c } \right) } \right) }^{ \frac { 3 }{ 2 } } }{ \frac { 1 }{ c } \sec ^{ 2 }{ \left( \frac { x }{ c } \right) } } \\ \Rightarrow \rho =\frac { { c\left( \sec ^{ 2 }{ \left( \frac { x }{ c } \right) } \right) }^{ \frac { 3 }{ 2 } } }{ \sec ^{ 2 }{ \left( \frac { x }{ c } \right) } } \\ \Rightarrow \rho =\frac { c\sec ^{ 3 }{ \left( \frac { x }{ c } \right) } }{ \sec ^{ 2 }{ \left( \frac { x }{ c } \right) } } \\ \Rightarrow \rho =c\sec { \left( \frac { x }{ c } \right) }
Example-2.y={ e }^{ -{ x }^{ 2 } }
Solution:–y={ e }^{ -{ x }^{ 2 } }
x के सापेक्ष अवकलन करने पर-
\frac { dy }{ dx } =\left( -2x \right) { e }^{ -{ x }^{ 2 } }\\ \Rightarrow \frac { dy }{ dx } =-2x{ e }^{ -{ x }^{ 2 } }
पुनः x के सापेक्ष अवकलन करने पर-
\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =-2{ e }^{ -{ x }^{ 2 } }-2x{ e }^{ -{ x }^{ 2 } }\left( -2x \right) \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =-2{ e }^{ -{ x }^{ 2 } }+4{ x }^{ 2 }{ e }^{ -{ x }^{ 2 } }\\ \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } } \\ \Rightarrow \rho =\frac { { \left( 1+4{ x }^{ 2 }{ e }^{ -2{ x }^{ 2 } } \right) }^{ \frac { 3 }{ 2 } } }{ { -2{ e }^{ -{ x }^{ 2 } }+4{ x }^{ 2 }{ e }^{ -{ x }^{ 2 } } } } \\ \Rightarrow \rho =\frac { { \left( 1+4{ x }^{ 2 }{ y }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { -2{ e }^{ -{ x }^{ 2 } }(2{ x }^{ 2 }-1) } } \\ \Rightarrow \rho =\frac { { \left( 1+4{ x }^{ 2 }{ y }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { 2y(2{ x }^{ 2 }-1) } } [संख्यात्मक मान लेने पर]
निम्न वक्रों के लिए उनके समक्ष दिए गए बिन्दुओं पर वक्रता-त्रिज्या ज्ञात कीजिए: (Find the radius of curvature of the following curves at the points indicated against them:)
Example-3. फोलियम (Folium) { x }^{ 3 }+{ y }^{ 3 }=3axy के \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) बिन्दु पर (at the point)
Solution– { x }^{ 3 }+{ y }^{ 3 }=3axy
x के सापेक्ष अवकलन करने पर-
3{ x }^{ 2 }+3{ y }^{ 2 }\left( \frac { dy }{ dx } \right) =3ay+3ax\left( \frac { dy }{ dx } \right) \\ \Rightarrow 3{ y }^{ 2 }\left( \frac { dy }{ dx } \right) -3ax\left( \frac { dy }{ dx } \right) =3ay-3{ x }^{ 2 }\\ \Rightarrow \left( \frac { dy }{ dx } \right) \left( 3{ y }^{ 2 }-3ax \right) =3ay-3{ x }^{ 2 }\\ \Rightarrow \frac { dy }{ dx } =\frac { 3ay-3{ x }^{ 2 } }{ 3{ y }^{ 2 }-3ax } \\ \Rightarrow \frac { dy }{ dx } =\frac { ay-{ x }^{ 2 } }{ { y }^{ 2 }-ax }
पुनः x के सापेक्ष अवकलन करने पर-
\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { \left( { y }^{ 2 }-ax \right) \left( a\frac { dy }{ dx } -2x \right) -\left( ay-{ x }^{ 2 } \right) \left( 2y\frac { dy }{ dx } -a \right) }{ { \left( { y }^{ 2 }-ax \right) }^{ 2 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { \begin{matrix} \left( { y }^{ 2 }-ax \right) \left[ a\left( \frac { ay-{ x }^{ 2 } }{ { y }^{ 2 }-ax } \right) -2x \right] - \\ \left( ay-{ x }^{ 2 } \right) \left[ 2y\left( \frac { ay-{ x }^{ 2 } }{ { y }^{ 2 }-ax } \right) -a \right] \end{matrix} }{ { \left( { y }^{ 2 }-ax \right) }^{ 2 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { \begin{matrix} \left( { y }^{ 2 }-ax \right) \left[ \frac { { a }^{ 2 }y-a{ x }^{ 2 }-2x{ y }^{ 2 }+2a{ x }^{ 2 } }{ { y }^{ 2 }-ax } \right] - \\ \left( ay-{ x }^{ 2 } \right) \left[ \frac { 2a{ y }^{ 2 }-2{ x }^{ 2 }y-a{ y }^{ 2 }+{ a }^{ 2 }{ x } }{ { y }^{ 2 }-ax } \right] \end{matrix} }{ { \left( { y }^{ 2 }-ax \right) }^{ 2 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { \begin{matrix} \left( { y }^{ 2 }-ax \right) \left( { a }^{ 2 }y-2x{ y }^{ 2 }+a{ x }^{ 2 } \right) - \\ \left( ay-{ x }^{ 2 } \right) \left( a{ y }^{ 2 }-2{ x }^{ 2 }y+{ a }^{ 2 }{ x } \right) \end{matrix} }{ { \left( { y }^{ 2 }-ax \right) }^{ 3 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { \begin{matrix} { a }^{ 2 }{ y }^{ 3 }-2x{ y }^{ 4 }+a{ x }^{ 2 }{ y }^{ 2 }-{ a }^{ 3 }xy+2a{ x }^{ 2 }{ y }^{ 2 }-{ a }^{ 2 }{ x }^{ 3 } \\ -{ a }^{ 2 }{ y }^{ 3 }+2a{ x }^{ 2 }{ y }^{ 2 }-{ a }^{ 3 }xy+a{ x }^{ 2 }{ y }^{ 2 }-2{ x }^{ 4 }y+{ a }^{ 2 }{ x }^{ 3 } \end{matrix} }{ { \left( { y }^{ 2 }-ax \right) }^{ 3 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { -2x{ y }^{ 4 }-2{ x }^{ 4 }y+6a{ x }^{ 2 }{ y }^{ 2 }-2{ a }^{ 3 }xy }{ { \left( { y }^{ 2 }-ax \right) }^{ 3 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { -2xy\left( { x }^{ 3 }+{ y }^{ 3 }-3axy \right) -2{ a }^{ 3 }xy }{ { \left( { y }^{ 2 }-ax \right) }^{ 3 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { -2xy\left( 0 \right) -2{ a }^{ 3 }xy }{ { \left( { y }^{ 2 }-ax \right) }^{ 3 } } \\ \Rightarrow \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { -2{ a }^{ 3 }xy }{ { \left( { y }^{ 2 }-ax \right) }^{ 3 } } \\ { \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { -2{ a }^{ 3 }\left( \frac { 3a }{ 2 } \right) \left( \frac { 3a }{ 2 } \right) }{ { \left[ { \left( \frac { 3a }{ 2 } \right) }^{ 2 }-a\left( \frac { 3a }{ 2 } \right) \right] }^{ 3 } } \\ \Rightarrow { \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { -2{ a }^{ 3 }\times \frac { 9{ a }^{ 2 } }{ 4 } }{ { \left( \frac { 9{ a }^{ 2 } }{ 4 } -\frac { 3{ a }^{ 2 } }{ 2 } \right) }^{ 3 } } \\ \Rightarrow { \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { -\frac { 9{ a }^{ 5 } }{ 2 } }{ { \left( \frac { 9{ a }^{ 2 }-6{ a }^{ 2 } }{ 4 } \right) }^{ 3 } } \\ \Rightarrow { \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { -\frac { 9{ a }^{ 5 } }{ 2 } }{ { \left( \frac { 3{ a }^{ 2 } }{ 4 } \right) }^{ 3 } } \\ \Rightarrow { \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=-\frac { 9{ a }^{ 5 } }{ 2 } \times \frac { 64 }{ 27{ a }^{ 5 } } \\ \Rightarrow { \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=-\frac { 32 }{ 3a } \\ \frac { dy }{ dx } =\frac { ay-{ x }^{ 2 } }{ { y }^{ 2 }-ax } \\ { \left( \frac { dy }{ dx } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { a\left( \frac { 3a }{ 2 } \right) -{ \left( \frac { 3a }{ 2 } \right) }^{ 2 } }{ { \left( \frac { 3a }{ 2 } \right) }^{ 2 }-a\left( \frac { 3a }{ 2 } \right) } \\ \Rightarrow { \left( \frac { dy }{ dx } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { \frac { 3{ a }^{ 2 } }{ 2 } -\frac { 9{ a }^{ 2 } }{ 4 } }{ \frac { 9{ a }^{ 2 } }{ 4 } -\frac { 3{ a }^{ 2 } }{ 2 } } \\ =\frac { 6{ a }^{ 2 }-9{ a }^{ 2 } }{ 4 } \times \frac { 4 }{ 9{ a }^{ 2 }-6{ a }^{ 2 } } \\ =\frac { -3{ a }^{ 2 } }{ 3{ a }^{ 2 } } \\ \Rightarrow { \left( \frac { dy }{ dx } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=-1\\ \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } } \\ \Rightarrow \rho =\frac { { \left[ 1+1 \right] }^{ \frac { 3 }{ 2 } } }{ \frac { -32 }{ 3a } } \\ \Rightarrow \rho =-\frac { 2\sqrt { 2 } }{ 32 } \left( 3a \right) \\ \Rightarrow \rho =\frac { 3\sqrt { 2 } a }{ 16 } [संख्यात्मक मान लेने पर]
Example-4. y=4\sin { x } -\sin { 2x } के उस बिन्दु पर जहां x=\frac { \pi }{ 2 } (at the point,where)
Solution–y=4\sin { x } -\sin { 2x }
x के सापेक्ष अवकलन करने पर-
\frac { dy }{ dx } =4\cos { x } -\cos { 2x } \\ { \left( \frac { dy }{ dx } \right) }_{ \left( x=\frac { \pi }{ 2 } \right) }=4\cos { \frac { \pi }{ 2 } } -2\cos { \pi } \\ \Rightarrow { \left( \frac { dy }{ dx } \right) }_{ \left( x=\frac { \pi }{ 2 } \right) }=4\left( 0 \right) -2\left( -1 \right) \\ \Rightarrow { \left( \frac { dy }{ dx } \right) }_{ \left( x=\frac { \pi }{ 2 } \right) }=2
पुनः x के सापेक्ष अवकलन करने पर-
\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =-4\sin { x } +4\sin { 2x } \\ \Rightarrow { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) }_{ \left( x=\frac { \pi }{ 2 } \right) }=-4\sin { \frac { \pi }{ 2 } } +4\sin { \pi } \\ \Rightarrow { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) }_{ \left( x=\frac { \pi }{ 2 } \right) }=-4\\ \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } } \\ \Rightarrow \rho =\frac { { \left( 1+{ 2 }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { -4 } } \\ \Rightarrow \rho =\frac { { 5 }^{ \frac { 3 }{ 2 } } }{ { -4 } } \\ \Rightarrow \rho =\frac { 5\sqrt { 5 } }{ 4 } [संख्यात्मक मान लेने पर]
Example-5. सिद्ध कीजिए कि परवलय { y }^{ 2 }=4ax के किसी बिन्दु P पर वक्रता-त्रिज्या वक्र तथा नियता के मध्य अभिलम्ब की लम्बाई की दुगुनी होती है।
(Show that in the parabola { y }^{ 2 }=4ax the radius of curvature at any point P is twice the length of the normal intercepted between the curve and the directrix.)
Solution-{ y }^{ 2 }=4ax
x के सापेक्ष अवकलन करने पर-
2y\frac { dy }{ dx } =4a\\ \Rightarrow \frac { dy }{ dx } =\frac { 2a }{ y }
पुनः x के सापेक्ष अवकलन करने पर-
\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =-\frac { 2a }{ { y }^{ 2 } } .\frac { dy }{ dx } \\ \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =-\frac { 2a }{ { y }^{ 2 } } .\frac { 2a }{ y } =\frac { -4{ a }^{ 2 } }{ { y }^{ 3 } } \\ \Rightarrow { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) }_{ \left( x,y \right) }=\frac { -4{ a }^{ 2 } }{ { y }^{ 3 } } \\ \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } } \\ \Rightarrow \rho =\frac { { \left( 1+{ \left( \frac { 2a }{ y } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \frac { -4{ a }^{ 2 } }{ { y }^{ 3 } } } } \\ \Rightarrow \rho =-\frac { { \left( { y }^{ 2 }+4{ a }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { y }^{ 3 } } \times \frac { { y }^{ 3 } }{ 4{ a }^{ 2 } } \\ \Rightarrow \rho =-\frac { { \left( 4ax+4{ a }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ 4{ a }^{ 2 } } \\ \Rightarrow \rho =-\frac { { \left( 4{ a } \right) }^{ \frac { 3 }{ 2 } }{ \left( x+{ a } \right) }^{ \frac { 3 }{ 2 } } }{ 4{ a }^{ 2 } } \\ \Rightarrow \rho =-\frac { 8a\sqrt { a } { \left( x+{ a } \right) }^{ \frac { 3 }{ 2 } } }{ 4{ a }^{ 2 } } \\ \Rightarrow \rho =\frac { 2{ \left( x+{ a } \right) }^{ \frac { 3 }{ 2 } } }{ \sqrt { a } } ....(1)[संख्यात्मक मान लेने पर]
अभिलम्ब का समीकरण-
(X-x)+(\frac { dy }{ dx } )(Y-y)=0\\ \Rightarrow (X-x)+\frac { 2a }{ y } (Y-y)=0\\ \Rightarrow Xy-xy+2aY-2ay=0\\ \Rightarrow Xy+2aY-xy-2ay=0...(2)
नियता का समीकरण X=-a ……(3)[/katex]
समीकरण (2) व (3) से-
\Rightarrow -ay+2aY-xy-2ay=0\\ \Rightarrow Y=\frac { xy+3ay }{ 2a }
नियता पर A बिन्दु के निर्देशांक
A(-a,\frac { xy+3ay }{ 2a } )
तथा वक्र पर स्थित बिन्दु P के निर्देशांक
P(x,y)
दोनों के बीच लम्बाई
PA=\sqrt { { (x+a) }^{ 2 }+{ (y-\frac { xy+3ay }{ 2a } ) }^{ 2 } } \\ =\sqrt { { (x+a) }^{ 2 }+{ (\frac { 2ay-xy-3ay }{ 2a } ) }^{ 2 } } \\ =\sqrt { { (x+a) }^{ 2 }+{ (\frac { -xy-ay }{ 2a } ) }^{ 2 } } \\ =\sqrt { { (x+a) }^{ 2 }+{ \frac { { y }^{ 2 }(x+a) }{ 4{ a }^{ 2 } } }^{ 2 } } \\ =\sqrt { { (x+a) }^{ 2 }[1+\frac { { y }^{ 2 } }{ 4{ a }^{ 2 } } ] } \\ =(x+a)\sqrt { 1+\frac { 4ax }{ 4{ a }^{ 2 } } } \\ =(x+a)\sqrt { 1+\frac { x }{ a } } \\ =(x+a)\sqrt { \frac { x+a }{ a } } \\ =\frac { { (x+a) }^{ \frac { 3 }{ 2 } } }{ \sqrt { a } } ...(4)
समीकरण (2) व (4) से-
2PA=\rho
उपर्युक्त उदाहरणों के द्वारा वक्रता त्रिज्या (Radius of Curvature) को समझ सकते हैं।
4.वक्रता त्रिज्या की समस्याएं (Radius of Curvature Problems)-
निम्न वक्रों के बिन्दु (x,y) पर वक्रता-त्रिज्या ज्ञात कीजिए:
(Find the radius of curvature at the point (x,y) on the following curves:)
(1)a{ y }^{ 2 }={ x }^{ 3 }\\ (2)xy={ c }^{ 2 }
(3.) वक्र y=a\cosh { (\frac { x }{ a } ) } के लिए सिद्ध कीजिए कि \rho =\frac { { y }^{ 2 } }{ a }
(For the curve y=a\cosh { (\frac { x }{ a } ) } prove that \rho =\frac { { y }^{ 2 } }{ a } )
(4.) यदि वक्र y=\frac { ax }{ a+x } के किसी बिन्दु (x,y) पर वक्रता-त्रिज्या \rho हो तो प्रदर्शित कीजिए कि { (\frac { 2\rho }{ a } ) }^{ \frac { 2 }{ 3 } }={ (\frac { x }{ y } ) }^{ 2 }+{ (\frac { y }{ x } ) }^{ 2 }
(For the curve y=\frac { ax }{ a+x } ,if \rho is the radius of curvature at any point (x,y) show that { (\frac { 2\rho }{ a } ) }^{ \frac { 2 }{ 3 } }={ (\frac { x }{ y } ) }^{ 2 }+{ (\frac { y }{ x } ) }^{ 2 })
(5.) सिद्ध कीजिए कि एस्ट्रायड { x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } }={ a }^{ \frac { 2 }{ 3 } } के किसी भी बिन्दु (x,y) पर वक्रता-त्रिज्या,मूलबिन्दु से स्पर्श-रेखा पर खींचे गए लम्ब की लम्बाई की तीन गुनी होती है।
(Show that the radius of curvature at any point (x,y) of the astroid { x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } }={ a }^{ \frac { 2 }{ 3 } } is three times perpendicular length dropped from the origin on the tangent.)
उत्तर-(1)\frac { 1 }{ 6a } \sqrt { x } { (4a+9x) }^{ \frac { 3 }{ 2 } }\\ (2)\frac { 1 }{ 2{ c }^{ 2 } } { ({ x }^{ 2 }+{ y }^{ 2 }) }^{ \frac { 3 }{ 2 } }
उपर्युक्त सवालों को हल करने पर वक्रता त्रिज्या (Radius of Curvature) ठीक से समझ में आ सकता है।
5.वक्रता-त्रिज्या का प्रतीक (Radius of Curvature symbol)-
\rho \\ \rho =\frac { { \left( 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { \left( \frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } \right) } }
6.वक्रता-त्रिज्या क्या है? (What is radius of curvature)-
- वक्रता त्रिज्या,वक्रता का व्युत्क्रम है।एक वक्र के लिए, यह वृत्ताकार चाप के त्रिज्या के बराबर होता है जो उस बिंदु पर वक्र को सबसे अच्छी तरह से अनुमानित करता है।सतहों के लिए, वक्रता की त्रिज्या एक वृत्त की त्रिज्या है जो सबसे अच्छी तरह से एक सामान्य खंड या संयोजन को जोड़ती है।
- उपर्युक्त विवरण के आधार पर वक्रता त्रिज्या (Radius of Curvature) को भली-भांति समझ सकते हैं।
Also Read This Article:-Pedal Equation of Curve
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |