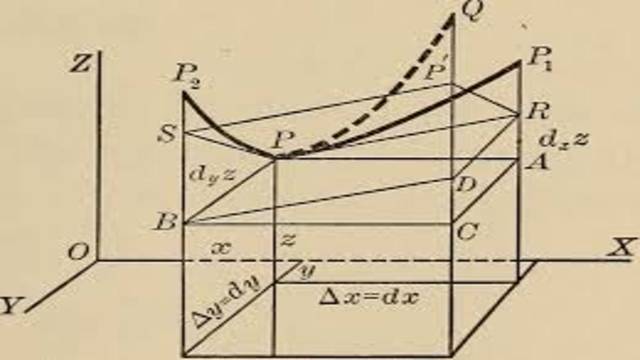
Total Differential Co-efficient
1.सम्पूर्ण अवकल गुणांक का परिचय (Introduction to Total Differential Co-efficient)-
(1.) f(x,y) का सम्पूर्ण अवकलज ज्ञात करें (x y)find the total derivative of f(x y)-
सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) में दो चर x एवं y फलन माना z=f(x,y) है। अब यदि x एवं y किसी अन्य चर t पर निर्भर करते हों तो\frac { dz }{ dt } ,z का t के सापेक्ष सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) है।जिसका मान निम्न प्रकार है-
\frac { dz }{ dt } =\frac { \partial z }{ \partial x } \frac { dx }{ dt } +\frac { \partial z }{ \partial y } \frac { dy }{ dt }
सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) में अचरों की संख्या दो से अधिक भी हो सकती है।
(2.)यदि u=f(x,y) जहां x=\phi \left( t \right) तथा y=\psi \left( t \right) तो x तथा y का मान t में,u=f(x,y) में रखने पर ,u का मान t के पदों में आ जाएगा।इस अवस्था में u एकल चर t का फलन होगा तथा साधारण अवकल गुणांक ज्ञात किया जा सकता है।\frac { dy }{ dt } को u का सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) कहते हैं, जिससे उसका आंशिक अवकल गुणांक \frac { \partial u }{ \partial x } तथा\frac { \partial u }{ \partial y } से भिन्नता प्रकट कर सके।आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Radius of curvature for polar equation
2.सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) के सूत्र की स्थापना,सम्पूर्ण अवकल की गणना कैसे की जाती है? (How is total differential calculated?), सम्पूर्ण अवकल प्रमाण (total differential proof),सम्पूर्ण अवकल की गणना कैसे की जाती है? (How is total differential calculated?)-
माना कि t में परिवर्तन\delta t के संगत x,y तथा u में परिवर्तन क्रमशः \delta x,\delta yतथा \delta u है।
u+\delta u=f\left( x+\delta x,y+\delta y \right)और\delta u=f\left( x+\delta x,y+\delta y \right) -f\left( x,y \right)
तो \frac { du }{ dt } की परिभाषानुसार
\frac { du }{ dt } =\underset { \delta t\rightarrow 0 }{ lim } \frac { \delta u }{ \delta t } =\underset { \delta t\rightarrow 0 }{ lim } \frac { f\left( x+\delta x,y+\delta y \right) -f\left( x,y \right) }{ \delta t } \\ =\underset { \delta t\rightarrow 0 }{ lim } \frac { f\left( x+\delta x,y+\delta y \right) -f\left( x,y+\delta y \right) +f\left( x,y+\delta y \right) -f\left( x,y \right) }{ \delta t } \\ =\underset { \delta t\rightarrow 0 }{ lim } \left\{ \frac { f\left( x+\delta x,y+\delta y \right) -f\left( x,y+\delta y \right) }{ \delta t } .\frac { \delta x }{ \delta t } +\frac { f\left( x,y+\delta y \right) -f\left( x,y \right) }{ \delta t } .\frac { \delta y }{ \delta t } \right\} ....(1)
जब \delta tशून्य की ओर प्रवृत्त करेगा तो परिणामत: \delta x,\delta yतथा \delta u भी शून्य की ओर प्रवृत्त करेंगे अतः
\lim _{ \delta t\rightarrow 0 }{ \frac { \delta x }{ \delta t } } =\frac { dx }{ dt } ,\lim _{ \delta t\rightarrow 0 }{ \frac { \delta y }{ \delta t } } =\frac { dy }{ dt }
अब आंशिक अवकलन की परिभाषानुसार
\lim _{ \delta y\rightarrow 0 }{ \frac { f\left( x,y+\delta y \right) -f\left( x,y \right) }{ \delta y } } =\frac { \partial f\left( x,y \right) }{ \partial y }
तथा \lim _{ \delta x\rightarrow 0 }{ \frac { f\left( x+\delta x,y+\delta y \right) -f\left( x,y+\delta y \right) }{ \delta x } } =\frac { f\left( x,y+\delta y \right) }{ \partial x }
का x के सापेक्ष अवकलज है। परन्तु जब \delta t\rightarrow 0 तो \delta y भी शून्य की ओर प्रवृत्त होगा। अतः यह x के सापेक्ष f(x,y) का अवकलज है जबकि यह मान लिया है कि x ही विचरित (vary) होता है, साथ ही दूसरा चर y अचर रहता है। अतः सीमा u=f(x,y) का x के सापेक्ष आंशिक अवकलज हुआ।
\therefore \lim _{ \delta x\rightarrow 0 }{ \frac { f\left( x+\delta x,y+\delta y \right) -f\left( x,y+\delta y \right) }{ \delta x } } =\frac { \partial f\left( x,y \right) }{ \partial x }
अतः (1) से,
या \frac { du }{ dt } =\frac { \partial f }{ \partial x } .\frac { dx }{ dt } +\frac { \partial f }{ \partial y } .\frac { dy }{ dt }
या \frac { du }{ dt } =\frac { \partial u }{ \partial x } .\frac { dx }{ dt } +\frac { \partial u }{ \partial y } .\frac { dy }{ dt }
व्यापकतया (in general) ,यदि f=f({ x }_{ 1 },{ x }_{ 2 },{ x }_{ 3 },...........{ x }_{ n }) तथा { x }_{ 1 },{ x }_{ 2 },{ x }_{ 3 },...........{ x }_{ n } सभी t के फलन हों तो ऊपर की भांति
\frac { du }{ dt } =\frac { \partial u }{ \partial { x }_{ 1 } } .\frac { d{ x }_{ 1 } }{ dt } +\frac { \partial u }{ \partial { x }_{ 2 } } .\frac { d{ x }_{ 2 } }{ dt } +...............+\frac { \partial u }{ \partial { x }_{ n } } .\frac { d{ x }_{ n } }{ dt }
प्राप्त किया जा सकता है।
3.सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) पर आधारित सवाल-
Question-1.यदि (If)u={ x }^{ 2 }+{ y }^{ 2 },\quad v=2xy
तथा (and) V=f\left( u,v \right) तो सिद्ध कीजिए कि (then prove that)
x\frac { \partial V }{ \partial x } -y\frac { \partial V }{ \partial y } =2{ ({ u }^{ 2 }-{ v }^{ 2 }) }^{ \frac { 1 }{ 2 } }.\frac { \partial V }{ \partial u }
Solution–u={ x }^{ 2 }+{ y }^{ 2 },\quad v=2xy,\quad V=f\left( u,v \right)
सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) के सूत्र से-
\frac { \partial V }{ \partial x } =\frac { \partial V }{ \partial u } .\frac { \partial u }{ \partial x } +\frac { \partial V }{ \partial v } .\frac { \partial v }{ \partial x } ....(1)\\ u={ x }^{ 2 }+{ y }^{ 2 }\\ \frac { \partial u }{ \partial x } =2x,\quad \quad \frac { \partial u }{ \partial y } =2y,\quad \quad \quad \frac { \partial v }{ \partial x } =2y\quad \quad \quad \frac { \partial v }{ \partial y } =2x
मान रखने पर-
\frac { \partial V }{ \partial x } =\frac { \partial V }{ \partial u } .2x+\frac { \partial V }{ \partial v } .2y\\ \Rightarrow \frac { \partial V }{ \partial x } =2x\frac { \partial V }{ \partial u } +2y\frac { \partial V }{ \partial v } \\ \Rightarrow x\frac { \partial V }{ \partial x } =2{ x }^{ 2 }\frac { \partial V }{ \partial u } +2xy\frac { \partial V }{ \partial v } ...(2)
पुनः\frac { \partial V }{ \partial y } =\frac { \partial V }{ \partial u } .\frac { \partial u }{ \partial y } +\frac { \partial V }{ \partial v } .\frac { \partial v }{ \partial y }
मान रखने पर-
\frac { \partial V }{ \partial y } =\frac { \partial V }{ \partial u } .2y+\frac { \partial V }{ \partial v } .2x\\ \Rightarrow \frac { \partial V }{ \partial y } =2y\frac { \partial V }{ \partial u } +2x\frac { \partial V }{ \partial v } \\ \Rightarrow y\frac { \partial V }{ \partial y } =2{ y }^{ 2 }\frac { \partial V }{ \partial u } +2xy\frac { \partial V }{ \partial v } ..(3)
समीकरण (2) में से (3) घटाने पर-
x\frac { \partial V }{ \partial x } -y\frac { \partial V }{ \partial y } =2{ (x }^{ 2 }-{ y }^{ 2 })\frac { \partial V }{ \partial u } ....(4)\\ { x }^{ 2 }-{ y }^{ 2 }=\sqrt { { ({ x }^{ 2 }+{ y }^{ 2 }) }^{ 2 }-{ 4x }^{ 2 }{ y }^{ 2 } } \\ { x }^{ 2 }-{ y }^{ 2 }={ ({ u }^{ 2 }-{ v }^{ 2 }) }^{ \frac { 1 }{ 2 } }...(5)
समीकरण (4) व (5) से-
Question-2.यदि (If)u=(a{ r }^{ n }+b{ r }^{ -n })(\cos { n\theta } +\sin { n\theta } ) सिद्ध कीजिए कि (prove that)
\frac { { \partial }^{ 2 }u }{ { \partial r }^{ 2 } } +\frac { 1 }{ r } .\frac { \partial u }{ \partial r } +\frac { 1 }{ { r }^{ 2 } } .\frac { { \partial }^{ 2 }u }{ { \partial \theta }^{ 2 } } =0
Solution–u=(a{ r }^{ n }+b{ r }^{ -n })(\cos { n\theta } +\sin { n\theta } )….(1)
r के सापेक्ष आंशिक अवकलन करने पर-
\Rightarrow \frac { \partial u }{ \partial r } =(an{ r }^{ n-1 }+bn{ r }^{ -n-1 })(\cos { n\theta } +\sin { n\theta } )…(2)
पुनः r के सापेक्ष आंशिक अवकलन करने पर-
\Rightarrow \frac { { \partial }^{ 2 }u }{ { \partial r }^{ 2 } } =[a(n-1)n{ r }^{ n-2 }+b(n-1)n{ r }^{ -n-2 }](\cos { n\theta } +\sin { n\theta } )….(3)
समीकरण (1) का \thetaके सापेक्ष अवकलन करने पर-
\frac { \partial u }{ \partial \theta } =(a{ r }^{ n }+b{ r }^{ -n })(-n\sin { n\theta } +n\cos { n\theta } )…(4)
पुनः \theta के सापेक्ष अवकलन करने पर-
\frac { { \partial }^{ 2 }u }{ { \partial \theta }^{ 2 } } =(a{ r }^{ n }+b{ r }^{ -n })(-{ n }^{ 2 }\cos { n\theta } -{ n }^{ 2 }\sin { n\theta } )…(5)
समीकरण (2) ,(3) व (5) से-
Question-3. सिद्ध कीजिए कि (prove that)
\Rightarrow \frac { { \partial }^{ 2 }u }{ { \partial x }^{ 2 } } +\frac { { \partial }^{ 2 }u }{ { \partial y }^{ 2 } } =\frac { { \partial }^{ 2 }u }{ { \partial \xi }^{ 2 } } +\frac { { \partial }^{ 2 }u }{ { \partial \eta }^{ 2 } }
जहां (where)x=\xi \cos { \alpha } -\eta \sin { \alpha } ,\quad \quad \quad y=\xi \sin { \alpha } -\eta \cos { \alpha }
Solution–x=\xi \cos { \alpha } -\eta \sin { \alpha } ,\quad \quad \quad y=\xi \sin { \alpha } -\eta \cos { \alpha }
सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) से-
\frac { \partial u }{ \partial \xi } =\frac { \partial u }{ \partial x } .\frac { \partial x }{ \partial \xi } +\frac { \partial u }{ \partial y } .\frac { \partial y }{ \partial \xi } ..(1)
तथा \frac { \partial u }{ \partial \eta } =\frac { \partial u }{ \partial x } .\frac { \partial x }{ \partial \eta } +\frac { \partial u }{ \partial y } .\frac { \partial y }{ \partial \eta }...(2) \\ x=\xi \cos { \alpha } -\eta \sin { \alpha } ,\quad y=\xi \sin { \alpha } -\eta \cos { \alpha } \\ \frac { \partial x }{ \partial \xi } =\cos { \alpha } ,\quad \frac { \partial x }{ \partial \eta } =-\sin { \alpha } ,\quad \frac { \partial y }{ \partial \xi } =\sin { \alpha } ,\quad \frac { \partial y }{ \partial \eta } =\cos { \alpha }
समीकरण (1) व (2) में मान रखने पर-
\frac { \partial u }{ \partial \xi } =\frac { \partial u }{ \partial x } \cos { \alpha } +\frac { \partial u }{ \partial y } \sin { \alpha }
पुनः अवकलन करने पर-
\frac { { \partial }^{ 2 }u }{ { \partial \xi }^{ 2 } } =\frac { { \partial }^{ 2 }u }{ { \partial x }^{ 2 } } .\frac { \partial x }{ \partial \xi } \cos { \alpha } +\frac { { \partial }^{ 2 }u }{ { \partial y }^{ 2 } } .\frac { \partial y }{ \partial \xi } \sin { \alpha } \\ \frac { { \partial }^{ 2 }u }{ { \partial \xi }^{ 2 } } =\frac { { \partial }^{ 2 }u }{ { \partial x }^{ 2 } } \cos ^{ 2 }{ \alpha } +\frac { { \partial }^{ 2 }u }{ { \partial y }^{ 2 } } \sin ^{ 2 }{ \alpha } ...(3)\\ \frac { \partial u }{ \partial \eta } =\frac { \partial u }{ \partial x } (-\sin { \alpha } )+\frac { \partial u }{ \partial y } \cos { \alpha }
पुनः अवकलन करने पर-
\frac { { \partial }^{ 2 }u }{ { \partial \eta }^{ 2 } } =-\frac { { \partial }^{ 2 }u }{ { \partial x }^{ 2 } } .\frac { \partial x }{ \partial \eta } \sin { \alpha } +\frac { { \partial }^{ 2 }u }{ { \partial y }^{ 2 } } .\frac { \partial y }{ \partial \eta } \cos { \alpha } \\ \frac { { \partial }^{ 2 }u }{ { \partial \xi }^{ 2 } } =\frac { { \partial }^{ 2 }u }{ { \partial x }^{ 2 } } \sin ^{ 2 }{ \alpha } +\frac { { \partial }^{ 2 }u }{ { \partial y }^{ 2 } } \cos ^{ 2 }{ \alpha } …(4)
समीकरण (3) व (4) को जोड़ने पर-
Question-4.यदि(If) x=r\cos { \theta } , y=r\sin { \theta } जहां rतथा \theta ,t के फलन हों (then prove that)
(1)\frac { dx }{ dt } =\cos { \theta } \frac { dr }{ dt } -r\sin { \theta } \frac { d\theta }{ dt }
(2)\frac { dy }{ dt } =\sin { \theta } \frac { dr }{ dt } +r\cos { \theta } \frac { d\theta }{ dt }
(3)\frac { { { d }^{ 2 }x } }{ d{ { t }^{ 2 } } } =\left[ \frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } -r{ \left( \frac { d\theta }{ dt } \right) }^{ 2 } \right] \cos { \theta } -(2\frac { dr }{ dt } .\frac { d\theta }{ dt } +r\frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } )\sin { \theta }
(4)\frac { { { d }^{ 2 }y } }{ d{ { t }^{ 2 } } } =\left[ \frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } -r{ \left( \frac { d\theta }{ dt } \right) }^{ 2 } \right] \sin { \theta } +(2\frac { dr }{ dt } .\frac { d\theta }{ dt } +r\frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } )\cos { \theta }
Solution-x=r\cos { \theta } ,\quad y=r\sin { \theta } \\ \frac { dx }{ dr } =\cos { \theta } ,\frac { dx }{ d\theta } =-r\sin { \theta } ,\frac { dy }{ dr } =\sin { \theta } ,\frac { dy }{ d\theta } =r\cos { \theta }
(1.) सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) से-
\frac { dx }{ dt } =\frac { dx }{ dr } .\frac { dr }{ dt } +\frac { dx }{ d\theta } .\frac { d\theta }{ dt }
मान रखने पर-
\frac { dx }{ dt } =\cos { \theta } \frac { dr }{ dt } -r\sin { \theta } \frac { d\theta }{ dt } …(1)
(2.) सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) से-
\frac { dy }{ dt } =\frac { dy }{ dr } .\frac { dr }{ dt } +\frac { dy }{ d\theta } .\frac { d\theta }{ dt }
मान रखने पर-
\frac { dy }{ dt } =\sin { \theta } \frac { dr }{ dt } +r\cos { \theta } \frac { d\theta }{ dt } …(2)
(3.) समीकरण (1) का पुनः अवकलन करने पर-
\frac { { { d }^{ 2 }x } }{ d{ { t }^{ 2 } } } =\frac { d }{ dt } (\cos { \theta } \frac { dr }{ dt } )-\frac { d }{ dt } (r\sin { \theta } \frac { d\theta }{ dt } )\\ \Rightarrow \frac { { { d }^{ 2 }x } }{ d{ { t }^{ 2 } } } =-\sin { \theta } \frac { d\theta }{ dt } \frac { dr }{ dt } +\cos { \theta } \frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } -\sin { \theta } \frac { dr }{ dt } \frac { d\theta }{ dt } \\ -r\cos { \theta } \frac { d\theta }{ dt } .\frac { d\theta }{ dt } -r\sin { \theta } \frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } \\ \Rightarrow \frac { { { d }^{ 2 }x } }{ d{ { t }^{ 2 } } } =(\frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } -r\frac { d\theta }{ dt } .\frac { d\theta }{ dt } )\cos { \theta } -(r\frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } +2\frac { d\theta }{ dt } \frac { dr }{ dt } )\sin { \theta } \\ \Rightarrow \frac { { { d }^{ 2 }x } }{ d{ { t }^{ 2 } } } =(\frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } -r{ \left( \frac { d\theta }{ dt } \right) }^{ 2 })\cos { \theta } -(r\frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } +2\frac { d\theta }{ dt } \frac { dr }{ dt } )\sin { \theta }
(4.) समीकरण (2) का पुनः अवकलन करने पर-
\frac { { { d }^{ 2 }y } }{ d{ { t }^{ 2 } } } =\frac { d }{ dt } (\sin { \theta } \frac { dr }{ dt } )+\frac { d }{ dt } (r\cos { \theta } \frac { d\theta }{ dt } )\\ \Rightarrow \frac { { { d }^{ 2 }y } }{ d{ { t }^{ 2 } } } =\cos { \theta } \frac { d\theta }{ dt } \frac { dr }{ dt } +\sin { \theta } \frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } \\ +\cos { \theta } \frac { dr }{ dt } \frac { d\theta }{ dt } -r\sin { \theta } { \left( \frac { d\theta }{ dt } \right) }^{ 2 }+r\cos { \theta } \frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } \\ \Rightarrow \frac { { { d }^{ 2 }y } }{ d{ { t }^{ 2 } } } =(r\frac { { { d }^{ 2 }\theta } }{ d{ { t }^{ 2 } } } +2\frac { dr }{ dt } \frac { d\theta }{ dt } )\cos { \theta } +(\frac { { { d }^{ 2 }r } }{ d{ { t }^{ 2 } } } -r{ \left( \frac { d\theta }{ dt } \right) }^{ 2 })\sin { \theta }
इस प्रकार उपर्युक्त सवालों के हल द्वारा सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) को समझा जा सकता है।
4.सम्पूर्ण अवकलज और सम्पूर्ण अवकल के बीच अंतर क्या है? (What is the difference between total derivative and total differential?)-
एक अवकलन रूप मूल अवकलनों का कोई औपचारिक रैखिक संयोजन है: जहां प्रत्येक चर का एक कार्य है। “सम्पूर्ण अवकलन” के विपरीत, जिसे हमने पहले देखा था, उन कार्यों के लिए किसी भी चीज के आंशिक अवकलन होने की कोई आवश्यकता नहीं है।
5.सम्पूर्ण अवकलज क्या है? (What is total derivative?)-
गणित में, एक बिंदु पर एक फ़ंक्शन का सम्पूर्ण अवकलज इसके तर्कों के संबंध में फ़ंक्शन के इस बिंदु के पास सबसे अच्छा रैखिक सन्निकटन है। आंशिक अवकलज के विपरीत, सम्पूर्ण अवकलज फ़ंक्शन को उसके सभी तर्कों के संबंध में बताता है, न कि केवल एक।
6.स्थिरांक का अवकल गुणांक क्या है? (What is the differential coefficient of a constant?)-
एक गुणांक आमतौर पर एक स्थिर मात्रा है, लेकिन f का अवकल गुणांक केवल एक अचर फलन है अगर f एक रैखिक फ़ंक्शन है। जब f रैखिक नहीं होता है, तो इसका अवकल गुणांक एक फ़ंक्शन होता है, इसे f’ कहें, जिसे f के अवकलन द्वारा व्युत्पन्न किया जाता है, इसलिए, आधुनिक शब्द, व्युत्पन्न।
स्थिरांक का अवकल गुणांक शून्य होता है।
7.सम्पूर्ण अवकल समीकरण (total differential equations)-
सम्पूर्ण अवकल समीकरण सम्पूर्ण अवकलज के संदर्भ में व्यक्त एक अवकल समीकरण है। चूंकि बाहरी अवकलज निर्देशांक-मुक्त है, इस अर्थ में जिसे तकनीकी अर्थ दिया जा सकता है, ऐसे समीकरण नैज और ज्यामितीय होते हैं।
8.सम्पूर्ण अवकलन अर्थशास्त्र (total differentiation economics)-
अर्थशास्त्र में, सम्पूर्ण अवकलज के लिए समीकरणों की प्रणाली के संदर्भ में उत्पन्न होना आम है। उदाहरण के लिए, एक सरल आपूर्ति-मांग प्रणाली एक उत्पाद की मात्रा q निर्दिष्ट कर सकती है, जो एक फ़ंक्शन D के रूप में मांग की जाती है, इसकी कीमत p और उपभोक्ताओं की आय I, बाद वाला एक बाहरी चर है, और उत्पादकों द्वारा आपूर्ति की गई मात्रा निर्दिष्ट कर सकती है। इसकी कीमत के एक फलन S के रूप में और दो बहिर्जात संसाधन लागत चर r और w। समीकरणों की परिणामी प्रणाली
q = D (p, l)
q= S (p,r,w),}
चर p और q के बाजार संतुलन मूल्यों को निर्धारित करता है। उदाहरण के लिए, r के संबंध में p का कुल व्युत्पन्न dp / dr है, जो बहिर्जात चर r को बाजार मूल्य की प्रतिक्रिया का संकेत और परिमाण देता है। संकेतित प्रणाली में, कुल छह संभावित कुल व्युत्पन्न होते हैं, जिन्हें इस संदर्भ में तुलनात्मक स्थिर व्युत्पत्ति के रूप में भी जाना जाता है: dp / dr, dp / dw, dp / dI, dq / dr, dq / dw, और db / dI। कुल व्युत्पन्न समीकरणों की प्रणाली को पूरी तरह से अलग करते हुए पाए जाते हैं, dr के माध्यम से विभाजित करते हुए कहते हैं, dq / dr और dp / dr को अज्ञात के रूप में मानते हुए, dI = dw = 0 की स्थापना करते हैं, और आमतौर पर दो पूरी तरह से भिन्न समीकरणों को एक साथ हल करके।
Cramer के नियम का उपयोग करना।
Also Read This Article:-Euler theorem of homogeneous function
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |