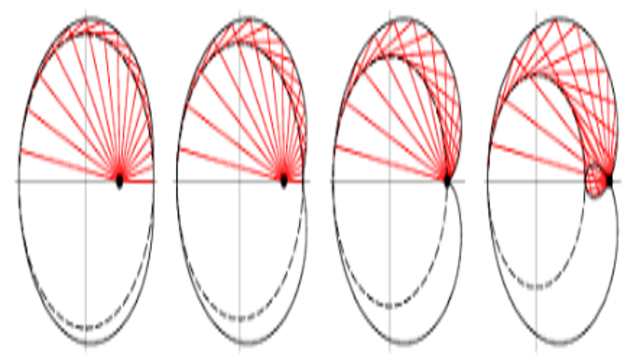
Pedal Equation of Curve
1.वक्र का पदिक समीकरण (Pedal Equation of Curve)-
वक्र का पदिक समीकरण (Pedal Equation of Curve)-किसी दिए हुए वक्र के लिए p तथा r के सम्बन्ध को उस वक्र का पदिक समीकरण कहते हैं, जहां p ध्रुव से वक्र के किसी बिन्दु p पर खींची गई स्पर्श रेखा पर लम्बवत दूरी है।
(1.)पदिक समीकरण ज्ञात करना जबकि वक्र का समीकरण कार्तीय रूप में हो (To find the pedal equation of curve whose equation is given in cartesian form)-
माना कि वक्र का समीकरण है:
f(x,y)=0 ……..(1)
तो { r }^{ 2 }={ x }^{ 2 }+{ y }^{ 2 }...(2)
किसी बिन्दु (x,y) पर स्पर्श रेखा का समीकरण
Y-y=\frac { dy }{ dx } (X-x).....(3)
p=स्पर्श रेखा (3) पर (0,0) मूलबिन्दु से खींचे गए लम्ब की दूरी
=\frac { x\frac { dy }{ dx } -y }{ \sqrt { \{ 1+{ (\frac { dy }{ dx } ) }^{ 2 }\} } } ....(4)
अब (1),(2) तथा (4) से x,y का विलोपन करने पर वक्र का अभीष्ट पदिक समीकरण प्राप्त होता है।
(2)पदिक समीकरण ज्ञात करना जबकि वक्र का समीकरण ध्रुवी रूप में हो (To find the pedal equation of curve whose equation is given in polar form)-
माना वक्र का समीकरण है:r=f\left( \theta \right) ....(1)
तो \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } { (\frac { dr }{ d\theta } ) }^{ 2 }....(2)
समीकरण (1) तथा (2) से का विलोपन करने पर वक्र का अभीष्ट पदिक समीकरण प्राप्त होता है।
विकल्पत: हम जानते हैं कि
p =r\sin { \phi } तथा \tan { \phi } =r\frac { d\theta }{ dr }
इन दोनों समीकरणों तथा समीकरण r=f\left( \theta \right) से \theta व \phi का विलोपन कर पदिक समीकरण प्राप्त किया जा सकता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Total Differential Co-efficient
2.वक्र का पदिक समीकरण के उदाहरण (Pedal Equation of Curve Examples)-
निम्न कार्तीय वक्रों के पदिक समीकरण ज्ञात कीजिए (Find the pedal equation of the following curves)
Example-1. वृत्त (The circle){ x }^{ 2 }+{ y }^{ 2 }=2ax
Solution-{ x }^{ 2 }+{ y }^{ 2 }=2ax….(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर-
2x+2y\frac { dy }{ dx } =2a\\ \Rightarrow \frac { dy }{ dx } =\frac { 2a-2x }{ 2y } \\ \Rightarrow \frac { dy }{ dx } =\frac { a-x }{ y } ...(2)
वृत्त के बिन्दु (x,y) पर स्पर्श रेखा का समीकरण होगा
Y-y=\frac { a-x }{ y } (X-x)\\ \Rightarrow Yy-{ y }^{ 2 }=aX-ax-xX+{ x }^{ 2 }\\ \Rightarrow (a-x)X-Yy+{ x }^{ 2 }+{ y }^{ 2 }-ax=0...(3)
अब मूलबिन्दु से स्पर्श रेखा पर लम्ब की लम्बाई
p =\frac { { x }^{ 2 }+{ y }^{ 2 }-ax }{ \sqrt { { (a-x) }^{ 2 }+{ y }^{ 2 } } } \\ \Rightarrow p =\frac { { x }^{ 2 }+{ y }^{ 2 }-ax }{ \sqrt { { a }^{ 2 }{ +x }^{ 2 }-2ax+{ y }^{ 2 } } } \\ \Rightarrow p =\frac { { x }^{ 2 }+{ y }^{ 2 }-ax }{ \sqrt { { a }^{ 2 }+0 } } [समीकरण (1) से]
\Rightarrow p =\frac { { x }^{ 2 }+{ y }^{ 2 }-ax }{ a } \\ \Rightarrow p =\frac { 2ax-ax }{ a } [समीकरण (1) से]
\Rightarrow p =\frac { ax }{ a } \\ \Rightarrow p =x...(4)\\ { r }^{ 2 }={ x }^{ 2 }+{ y }^{ 2 }\\ { r }^{ 2 }={ x }^{ 2 }+2ax-{ x }^{ 2 }[समीकरण (1) से]
{ r }^{ 2 }=2ax....(5)
समीकरण (4) व (5) से-
{ r }^{ 2 }=2ap
Example-2.{ x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } }={ a }^{ \frac { 2 }{ 3 } }
Solution:-{ x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } }={ a }^{ \frac { 2 }{ 3 } }….(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर-
\frac { 2 }{ 3 } { x }^{ -\frac { 1 }{ 3 } }+\frac { 2 }{ 3 } { y }^{ -\frac { 1 }{ 3 } }\frac { dy }{ dx } =0\\ \Rightarrow \frac { dy }{ dx } =-\frac { { x }^{ -\frac { 1 }{ 3 } } }{ { y }^{ -\frac { 1 }{ 3 } } } \\ \Rightarrow \frac { dy }{ dx } =-(\frac { { y }^{ \frac { 1 }{ 3 } } }{ { x }^{ \frac { 1 }{ 3 } } } )...(2)
ऐस्ट्राॅयड के बिन्दु (x,y) पर स्पर्श रेखा का समीकरण होगा-
Y-y=\frac { dy }{ dx } (X-x)\\ \Rightarrow Y-y=-(\frac { { y }^{ \frac { 1 }{ 3 } } }{ { x }^{ \frac { 1 }{ 3 } } } )(X-x)\\ \Rightarrow { x }^{ \frac { 1 }{ 3 } }Y-{ x }^{ \frac { 1 }{ 3 } }y=-{ y }^{ \frac { 1 }{ 3 } }X+{ y }^{ \frac { 1 }{ 3 } }x\\ \Rightarrow { y }^{ \frac { 1 }{ 3 } }X+{ x }^{ \frac { 1 }{ 3 } }Y-{ x }^{ \frac { 1 }{ 3 } }y-{ y }^{ \frac { 1 }{ 3 } }x=0\\ \Rightarrow { y }^{ \frac { 1 }{ 3 } }X+{ x }^{ \frac { 1 }{ 3 } }Y-{ x }^{ \frac { 1 }{ 3 } }{ y }^{ \frac { 1 }{ 3 } }({ x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } })=0\\ \Rightarrow { y }^{ \frac { 1 }{ 3 } }X+{ x }^{ \frac { 1 }{ 3 } }Y-{ x }^{ \frac { 1 }{ 3 } }{ y }^{ \frac { 1 }{ 3 } }{ a }^{ \frac { 2 }{ 3 } }=0[समीकरण (1) से]….(3)
अब मूलबिन्दु से स्पर्श रेखा पर लम्ब की लम्बाई-
p =\frac { { x }^{ \frac { 1 }{ 3 } }{ y }^{ \frac { 1 }{ 3 } }{ a }^{ \frac { 2 }{ 3 } } }{ \sqrt { { x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } } } } \\ \Rightarrow p =\frac { { x }^{ \frac { 1 }{ 3 } }{ y }^{ \frac { 1 }{ 3 } }{ a }^{ \frac { 2 }{ 3 } } }{ \sqrt { { a }^{ \frac { 2 }{ 3 } } } } [समीकरण (1) से]
\Rightarrow p =\frac { { x }^{ \frac { 1 }{ 3 } }{ y }^{ \frac { 1 }{ 3 } }{ a }^{ \frac { 2 }{ 3 } } }{ { a }^{ \frac { 1 }{ 3 } } } \\ \Rightarrow p ={ a }^{ \frac { 1 }{ 3 } }{ x }^{ \frac { 1 }{ 3 } }{ y }^{ \frac { 1 }{ 3 } }...(4)
समीकरण (1) से-
{ x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } }={ a }^{ \frac { 2 }{ 3 } }\\ \Rightarrow { ({ x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } }) }^{ 3 }={ a }^{ 2 }\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+3{ x }^{ \frac { 2 }{ 3 } }{ y }^{ \frac { 2 }{ 3 } }({ x }^{ \frac { 2 }{ 3 } }+{ y }^{ \frac { 2 }{ 3 } })={ a }^{ 2 }\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+3{ x }^{ \frac { 2 }{ 3 } }{ y }^{ \frac { 2 }{ 3 } }({ a }^{ \frac { 2 }{ 3 } })={ a }^{ 2 }[समीकरण (1) से]
\Rightarrow { x }^{ 2 }+{ y }^{ 2 }+3{ x }^{ \frac { 2 }{ 3 } }{ y }^{ \frac { 2 }{ 3 } }{ a }^{ \frac { 2 }{ 3 } }={ a }^{ 2 }\\ \Rightarrow { r }^{ 2 }+3{ p }^{ 2 }={ a }^{ 2 }[\because { r }^{ 2 }={ x }^{ 2 }+{ y }^{ 2 }]
निम्न ध्रुवीय वक्रों के पदिक समीकरण ज्ञात कीजिए (Find the pedal equation of the following curves:)
Example-3.{ r }^{ 2 }\cos { 2\theta } ={ a }^{ 2 }(अतिपरवलय)
Solution-{ r }^{ 2 }\cos { 2\theta } ={ a }^{ 2 }…(1)
\theta के सापेक्ष अवकलन करने पर-
\Rightarrow 2r\frac { dr }{ d\theta } \cos { 2\theta } -2{ r }^{ 2 }\sin { 2\theta } =0\\ \Rightarrow \frac { dr }{ d\theta } =\frac { 2{ r }^{ 2 }\sin { 2\theta } }{ 2r\cos { 2\theta } } \\ \Rightarrow \frac { dr }{ d\theta } =\frac { { r }\sin { 2\theta } }{ \cos { 2\theta } } \\ \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } { (\frac { dr }{ d\theta } ) }^{ 2 }\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } { (\frac { { r }\sin { 2\theta } }{ \cos { 2\theta } } ) }^{ 2 }\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } \frac { { r }^{ 2 }{ \sin ^{ 2 }{ 2\theta } } }{ \cos ^{ 2 }{ 2\theta } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 2 } } \frac { { \sin ^{ 2 }{ 2\theta } } }{ \cos ^{ 2 }{ 2\theta } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 2 } } \frac { { (1-\cos ^{ 2 }{ 2\theta } ) } }{ \cos ^{ 2 }{ 2\theta } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 2 } } (1-\frac { { a }^{ 4 } }{ { r }^{ 4 } } )\frac { { r }^{ 4 } }{ { a }^{ 4 } } [समीकरण (1) से]
\Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { r }^{ 2 } }{ { a }^{ 4 } } -\frac { 1 }{ { r }^{ 2 } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { { r }^{ 2 } }{ { a }^{ 4 } } \\ \Rightarrow { p }^{ 2 }=\frac { { a }^{ 4 } }{ { r }^{ 4 } } \\ \Rightarrow { p }^{ 2 }{ r }^{ 4 }={ a }^{ 4 }\\ \Rightarrow pr={ a }^{ 2 }
Example-4.{ r }^{ 2 }\cos { 2\theta } ={ a }^{ 2 }(लेमनिस्केट)
Solution-{ r }^{ 2 }\cos { 2\theta } ={ a }^{ 2 }…(1)
\theta के सापेक्ष अवकलन करने पर-
\Rightarrow 2r\frac { dr }{ d\theta } =-2{ a }^{ 2 }\sin { 2\theta } \\ \Rightarrow \frac { dr }{ d\theta } =-\frac { 2{ a }^{ 2 }\sin { 2\theta } }{ r } \\ \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } { (\frac { dr }{ d\theta } ) }^{ 2 }\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } \frac { { a }^{ 4 }{ \sin ^{ 2 }{ 2\theta } } }{ { r }^{ 2 } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 4 } }{ { r }^{ 6 } } \sin ^{ 2 }{ 2\theta } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 4 } }{ { r }^{ 6 } } (1-\cos ^{ 2 }{ 2\theta } )\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 4 } }{ { r }^{ 6 } } (1-\frac { { r }^{ 4 } }{ { a }^{ 4 } } )[समीकरण (1) से]
\Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 4 } }{ { r }^{ 6 } } -\frac { 1 }{ { r }^{ 2 } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { { a }^{ 4 } }{ { r }^{ 6 } } \\ \Rightarrow { p }^{ 2 }{ a }^{ 4 }={ r }^{ 6 }\\ \Rightarrow p{ a }^{ 2 }={ r }^{ 3 }\\ \Rightarrow { r }^{ 3 }=p{ a }^{ 2 }
Example-5.{ r }^{ n }={ a }^{ n }\cos { n\theta } (कोज्या सर्पिल)
Solution-{ r }^{ n }={ a }^{ n }\cos { n\theta } …(1)
\theta के सापेक्ष अवकलन करने पर-
\Rightarrow n{ r }^{ n-1 }\frac { dr }{ d\theta } =-n{ a }^{ n }\sin { n\theta } \\ \Rightarrow \frac { dr }{ d\theta } =-\frac { { a }^{ n }\sin { n\theta } }{ { r }^{ n-1 } } \\ \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } { (\frac { dr }{ d\theta } ) }^{ 2 }\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } (\frac { { a }^{ 2n }{ \sin ^{ 2 }{ n\theta } } }{ { r }^{ 2n-2 } } )\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } \frac { { a }^{ 2n } }{ { r }^{ 2n-2 } } \sin ^{ 2 }{ n\theta } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 2n } }{ { r }^{ 2n+2 } } (1-\cos ^{ 2 }{ n\theta } )\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 2n } }{ { r }^{ 2n+2 } } (1-\frac { { r }^{ 2n } }{ { a }^{ 2n } } )[समीकरण (1) से]
\Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 2n } }{ { r }^{ 2n+2 } } -\frac { 1 }{ { r }^{ 2 } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { { a }^{ 2n } }{ { r }^{ 2n+2 } } \\ \Rightarrow { p }^{ 2 }{ a }^{ 2n }={ r }^{ 2n+2 }\\ \Rightarrow p{ a }^{ n }={ r }^{ n+1 }\\ \Rightarrow { r }^{ n+1 }=p{ a }^{ n }
Example-6.a\theta ={ ({ r }^{ 2 }-{ a }^{ 2 }) }^{ \frac { 1 }{ 2 } }-a\cos ^{ -1 }{ (\frac { a }{ r } ) }
Solution-a\theta ={ ({ r }^{ 2 }-{ a }^{ 2 }) }^{ \frac { 1 }{ 2 } }-a\cos ^{ -1 }{ (\frac { a }{ r } ) } ….(1)
\theta के सापेक्ष अवकलन करने पर-
a=\frac { 2r }{ 2\sqrt { { r }^{ 2 }-{ a }^{ 2 } } } \frac { dr }{ d\theta } +a(-\frac { 1 }{ \sqrt { 1-\frac { { a }^{ 2 } }{ { r }^{ 2 } } } } )(\frac { { a } }{ { r }^{ 2 } } )\frac { dr }{ d\theta } \\ \Rightarrow a=(\frac { r }{ \sqrt { { r }^{ 2 }-{ a }^{ 2 } } } -\frac { { a }^{ 2 } }{ { r }^{ 2 }\sqrt { 1-\frac { { a }^{ 2 } }{ { r }^{ 2 } } } } )\frac { dr }{ d\theta } \\ \Rightarrow a=(\frac { r }{ \sqrt { { r }^{ 2 }-{ a }^{ 2 } } } -\frac { { a }^{ 2 } }{ { r }\sqrt { { r }^{ 2 }-{ a }^{ 2 } } } )\frac { dr }{ d\theta } \\ \Rightarrow a=(\frac { { { r }^{ 2 }-a }^{ 2 } }{ { r }\sqrt { { r }^{ 2 }-{ a }^{ 2 } } } )\frac { dr }{ d\theta } \\ \Rightarrow a=(\frac { \sqrt { { r }^{ 2 }-{ a }^{ 2 } } }{ { r } } )\frac { dr }{ d\theta } \\ \Rightarrow \frac { dr }{ d\theta } =\frac { ar }{ \sqrt { { r }^{ 2 }-{ a }^{ 2 } } } \\ \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } { (\frac { dr }{ d\theta } ) }^{ 2 }\\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { 1 }{ { r }^{ 4 } } .\frac { { a }^{ 2 }{ r }^{ 2 } }{ { r }^{ 2 }-{ a }^{ 2 } } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { r }^{ 2 } } +\frac { { a }^{ 2 } }{ { r }^{ 2 }({ r }^{ 2 }-{ a }^{ 2 }) } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { { { r }^{ 2 }-{ a }^{ 2 }+a }^{ 2 } }{ { r }^{ 2 }({ r }^{ 2 }-{ a }^{ 2 }) } \\ \Rightarrow \frac { 1 }{ { p }^{ 2 } } =\frac { { { r }^{ 2 } } }{ { r }^{ 2 }({ r }^{ 2 }-{ a }^{ 2 }) } \\ \Rightarrow { p }^{ 2 }={ r }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow { r }^{ 2 }={ a }^{ 2 }+{ p }^{ 2 }
Example-7.सिद्ध कीजिए कि वक्रx=2a\cos { \theta } -a\cos { 2\theta } ,y=2a\sin { \theta } -a\sin { 2\theta } का पदिक समीकरण 9({ r }^{ 2 }-{ a }^{ 2 })=8{ p }^{ 2 } होता है।
(Show that the pedal equation of the curve x=2a\cos { \theta } -a\cos { 2\theta } ,y=2a\sin { \theta } -a\sin { 2\theta } is 9({ r }^{ 2 }-{ a }^{ 2 })=8{ p }^{ 2 } )
Solution-x=2a\cos { \theta } -a\cos { 2\theta } ,y=2a\sin { \theta } -a\sin { 2\theta }
\theta के सापेक्ष अवकलन करने पर-
\frac { dx }{ d\theta } =-2a\sin { \theta } +2a\sin { 2\theta } \\ \frac { dy }{ d\theta } =2a\cos { \theta } -2a\cos { 2\theta } \\ \frac { dy }{ dx } =\frac { \frac { dy }{ d\theta } }{ \frac { dx }{ d\theta } } \\ \Rightarrow \frac { dy }{ dx } =\frac { 2a\cos { \theta } -2a\cos { 2\theta } }{ 2a\sin { 2\theta } -2a\sin { \theta } } \\ \Rightarrow \frac { dy }{ dx } =\frac { \cos { \theta } -\cos { 2\theta } }{ \sin { 2\theta } -\sin { \theta } }
स्पर्श रेखा का समीकरण-
Y-y=\frac { dy }{ dx } (X-x)\\ Y-2a\sin { \theta } +a\sin { 2\theta } =\frac { \cos { \theta } -\cos { 2\theta } }{ \sin { 2\theta } -\sin { \theta } } (X-2a\cos { \theta } +a\cos { 2\theta } )\\ \Rightarrow (\sin { 2\theta } -\sin { \theta } )Y-2a\sin { \theta } \sin { 2\theta } +2a\sin ^{ 2 }{ \theta } +a\sin ^{ 2 }{ 2\theta } -a\sin { 2\theta } \sin { \theta } =(\cos { \theta } -\cos { 2\theta } )X-2a\cos ^{ 2 }{ \theta } +2a\cos { \theta } \cos { 2\theta } +a\cos { \theta } \cos { 2\theta } -a\cos ^{ 2 }{ 2\theta } \\ \Rightarrow (\cos { \theta } -\cos { 2\theta } )X-(\sin { 2\theta } -\sin { \theta } )Y-2a(\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } )-a(\sin ^{ 2 }{ 2\theta } +\cos ^{ 2 }{ 2\theta } )+3a(\cos { \theta } \cos { 2\theta } +\sin { 2\theta } \sin { \theta } )=0\\ \Rightarrow (\cos { \theta } -\cos { 2\theta } )X-(\sin { 2\theta } -\sin { \theta } )Y-2a-a+3a\cos { \theta } =0\\ \Rightarrow (\cos { \theta } -\cos { 2\theta } )X-(\sin { 2\theta } -\sin { \theta } )Y-3a+3a\cos { \theta } =0
मूलबिन्दु (0,0) से स्पर्श रेखा पर लम्ब की लम्बाई
p=\left| \frac { 3a\cos { \theta } -3a }{ \sqrt { { (\cos { \theta } -\cos { 2\theta } ) }^{ 2 }+{ (\sin { 2\theta } -\sin { \theta } ) }^{ 2 } } } \right| \\ \Rightarrow p=\frac { 3a-3a\cos { \theta } }{ \sqrt { \cos ^{ 2 }{ \theta } +\cos ^{ 2 }{ 2\theta } -2\cos { \theta } \cos { 2\theta } +\sin ^{ 2 }{ \theta } +\sin ^{ 2 }{ 2\theta } -2\sin { 2\theta } \sin { \theta } } } \\ \Rightarrow p=\frac { 3a-3a\cos { \theta } }{ \sqrt { 1+1-2(\cos { \theta } \cos { 2\theta } +\sin { 2\theta } \sin { \theta ) } } } \\ \Rightarrow p=\frac { 3a-3a\cos { \theta } }{ \sqrt { 2-2\cos { \theta } } } \\ \Rightarrow p=\frac { 3a(1-\cos { \theta ) } }{ \sqrt { 2(1-\cos { \theta ) } } } \\ \Rightarrow p=\frac { 3a\sqrt { (1-\cos { \theta ) } } }{ \sqrt { 2 } } \\ \Rightarrow { p }^{ 2 }=\frac { 9{ a }^{ 2 }(1-\cos { \theta ) } }{ 2 } ....(2)\\ \Rightarrow { r }^{ 2 }={ x }^{ 2 }+{ y }^{ 2 }\\ \Rightarrow { r }^{ 2 }={ (2a\cos { \theta } -a\cos { 2\theta } ) }^{ 2 }+{ (2a\sin { \theta } -a\sin { 2\theta } ) }^{ 2 }\\ \Rightarrow { r }^{ 2 }=4{ a }^{ 2 }\cos ^{ 2 }{ \theta } +{ a }^{ 2 }\cos ^{ 2 }{ 2\theta } -4{ a }^{ 2 }\cos { \theta } \cos { 2\theta } +4{ a }^{ 2 }\sin ^{ 2 }{ \theta } +{ a }^{ 2 }\sin ^{ 2 }{ 2\theta } -4{ a }^{ 2 }\sin { 2\theta } \sin { \theta } \\ \Rightarrow { r }^{ 2 }=4{ a }^{ 2 }(\cos ^{ 2 }{ \theta } +\sin ^{ 2 }{ \theta } )+{ a }^{ 2 }(\cos ^{ 2 }{ 2\theta } +\sin ^{ 2 }{ 2\theta } )-4{ a }^{ 2 }(\cos { \theta } \cos { 2\theta } +\sin { 2\theta } \sin { \theta } )\\ \Rightarrow { r }^{ 2 }=4{ a }^{ 2 }+{ a }^{ 2 }-4{ a }^{ 2 }\cos { \theta } \\ \Rightarrow { r }^{ 2 }=5{ a }^{ 2 }-4{ a }^{ 2 }\cos { \theta } \\ \Rightarrow { r }^{ 2 }-{ a }^{ 2 }=4{ a }^{ 2 }(1-\cos { \theta } )....(3)
समीकरण (2) व (3) से-
{ p }^{ 2 }=\frac { 9{ a }^{ 2 } }{ 2 } \times \frac { { r }^{ 2 }-{ a }^{ 2 } }{ 4{ a }^{ 2 } } \\ \Rightarrow 8{ p }^{ 2 }=9({ r }^{ 2 }-{ a }^{ 2 })
उपर्युक्त उदाहरणों के द्वारा वक्र का पदिक समीकरण (Pedal Equation of Curve) को समझ सकते हैं।
3.वक्र का पदिक समीकरण की समस्याएं(Pedal Equation of Curve Problems)-
निम्न कार्तीय वक्रों के पदिक समीकरण ज्ञात कीजिए:(Find the pedal equation of the following cartesian curves:)
(1.)अतिपरवलय (The Hyperbola)\frac { { x }^{ 2 } }{ { a }^{ 2 } } -\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1
(2.)आयतीय अतिपरललय (Rectangular Hyperbola){ x }^{ 2 }-{ a }^{ 2 }={ a }^{ 2 }
निम्न ध्रुवीय वक्रों के पदिक समीकरण ज्ञात कीजिए:(Find the pedal equation of the following polar curves:)
(3.){ r }^{ n }={ a }^{ n }\sin { n\theta } (ज्या सर्पिल)
(4.)r=a\theta (आर्कमिडीज का सर्पिल)
(5)r=a(1+\cos { \theta } )
(6.)r=a(1-\cos { \theta } )(हृदयाभ)
Ans:-(1)\frac { 1 }{ { p }^{ 2 } } =\frac { 1 }{ { a }^{ 2 } } -\frac { 1 }{ { b }^{ 2 } } +\frac { { r }^{ 2 } }{ { a }^{ 2 }{ b }^{ 2 } } \\ (2)pr={ a }^{ 2 }\\ (3)p{ a }^{ n }={ a }^{ n+1 }\\ (4){ p }^{ 2 }=\frac { { r }^{ 4 } }{ { r }^{ 2 }+{ a }^{ 2 } } \\ (5){ p }^{ 2 }=\frac { { r }^{ 3 } }{ 2a } \\ (6){ p }^{ 2 }=ar
उपर्युक्त सवालों को हल करने पर वक्र का पदिक समीकरण (Pedal Equation of Curve) को ठीक से समझा जा सकता है।
4.आप एक वक्र के नैज समीकरण का कैसे ज्ञात करते हैं? (How do you find the intrinsic equation of a curve?)-
एक वक्र का नैज समीकरण इसकी चाप की लंबाई s को कोण ψ से जोड़ता है जो इसकी स्पर्शरेखा एक निश्चित दिशा (आमतौर पर s = 0 जब ψ = 0) के साथ बनाती है। हमें कर्व के साथ उस अर्थ को भी निर्दिष्ट करना होगा जिसमें वृद्धि होती है।उदाहरण के लिए, त्रिज्या ρ के एक वृत्त के नैज समीकरण को s = ρψ लिखा जा सकता है।
5.आप वक्रता की त्रिज्या कैसे खोजते हैं? (How do you find the radius of curvature?)-
एक बिंदु M (x, y) पर किसी वक्र की वक्रता की त्रिज्या को इस बिंदु पर वक्रता K का व्युत्क्रम कहा जाता है: R = 1K। इसलिए स्पष्ट समीकरण y = f (x) द्वारा दिए गए समतल वक्रों के लिए, एक बिंदु M (x, y) पर वक्रता की त्रिज्या निम्नलिखित अभिव्यक्ति द्वारा दी गई है: R = \frac { { [1+{ ({ y }^{ \prime }(x)) }^{ 2 }] }^{ \frac { 3 }{ 2 } } }{ { y }^{ \prime \prime }(x) } ।
6.पैराबोला का पेडल समीकरण (Pedal equation of parabola)-
n Curve Pedal point Pedal equation
1 Circle with radius a Point on circumference pa={ r }^{ 2 }
−1 Line Point distance a from line p = a
1⁄2 Cardioid Cusp { p }^{ 2 }a={ r }^{ 3 }
−1⁄2 Parabola Focus { p }^{ 2 }=ar
2 Lemniscate of Bernoulli Center p{ a }^{ 2 }={ r }^{ 3 }
−2 Rectangular hyperbola Center rp={ a }^{ 2 }
7.हाइपरबोला का पेडल समीकरण (Pedal equation of ellipse)-
पेडल बिंदु के रूप में हाइपरबोला का पेडल वक्र इसके फोकस के साथ वृत्त है।पेडल बिंदु के रूप में इसके केंद्र के साथ एक आयताकार हाइपरबोला का पेडल एक लेमिनेट है।
ऊपर दिए गए समीकरण के साथ हाइपरबोला का बेड़ा लामे वक्र है
{ (ax) }^{ \frac { 2 }{ 3 } }-{ (by) }^{ \frac { 2 }{ 3 } }={ (a+b) }^{ \frac { 2 }{ 3 } }।
8.वास्तविक जीवन में पेडल समीकरण के अनुप्रयोग (Applications of pedal equation in real life)-
कुछ वक्रों में विशेष रूप से सरल पेडल समीकरण होते हैं और एक वक्र के पेडल समीकरण को जानने से इसके गुण जैसे वक्रता के कुछ की गणना सरल हो सकती है।ये निर्देशांक शास्त्रीय यांत्रिकी और खगोलीय यांत्रिकी में कुछ प्रकार की बल समस्याओं को हल करने के लिए भी उपयुक्त हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा वक्र का पदिक समीकरण (Pedal Equation of Curve) को ओर ठीक प्रकार से समझा जा सकता है।
Also Read This Article:-Lengths of chords of curvature
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |