Equation of Straight Lines
1.सरल रेखा का समीकरण (Equation of Straight Lines)-
सरल रेखा का समीकरण (Equation of Straight Lines) में
(1.) सरल रेखा (Straight Line)-
सरल रेखा एक चर बिंदु का बिंदुपथ है जिस पर किन्हीं दो बिंदुओं को सीधे मिलाने पर बिंदुपथ के अन्य सभी बिंदु भी इस पर स्थित हो।
(2.)सरल रेखा का समीकरण (Equation of Straight Lines)-
एक ऐसा समीकरण सरल रेखा का समीकरण कहलाता है जो कि सरल रेखा पर स्थित प्रत्येक बिंदु द्वारा संतुष्ट होता है और ऐसे बिंदु जो सरल रेखा पर नहीं होते उन्हें संतुष्ट नहीं करता।
(3.)अंत: खंड (Intercept)-
यदि सरल रेखा AB,भुजाक्ष और कोटि अक्ष को चित्र में क्रमशः A और B बिंदुओं पर काटती है तब
(i)OA को सरल रेखा AB का x-अक्ष पर अन्त:खण्ड कहते हैं।
(ii)OB को सरल रेखा का y-अक्ष पर अन्त:खण्ड कहते हैं।
(iii)OA और OB दोनों को (इसी क्रम में) सरल रेखा AB का अक्षों पर अन्त:खण्ड कहते हैं।
टिप्पणी : यदि AB क्रमशः OX’,OY’ पर हो तो अन्त:खण्ड ऋणात्मक होते हैं।
(4.)रेखा की प्रवणता (Slope of Straight Line)-
कोई सरल रेखा x-अक्ष के साथ धन दिशा में जो कोण बनाती है उस कोण की स्पर्शज्या को उस सरल रेखा की प्रवणता अथवा झुकाव (ढ़ाल) कहते हैं।
रेखा की प्रवणता को प्राय: m से प्रदर्शित किया जाता है। यदि AB सरल रेखा x-अक्ष के साथ में \theta धन दिशा में कोण बनाती है तो m=\tan \theta होता है।यदि AB सरल रेखा x-अक्ष के साथ में ऋण दिशा में \theta कोण बनाती है तो m=-\tan \theta होगा।
चूंकि x-अक्ष अथवा x-अक्ष के समांतर रेखा x-अक्ष की धन दिशा में 0° का कोण बनाती है,अतः x-अक्ष अथवा x-अक्ष के समान्तर रेखा की प्रवणता (ढ़ाल) m=\tan 0°=0 होगी।
इसी प्रकार y-अक्ष अथवा y-अक्ष के समान्तर रेखा की प्रवणता (ढ़ाल) m=\tan 90°=\infty होगी।
यदि रेखा अक्षों से समान कोण बनाती है अर्थात् x-अक्ष के साथ धन दिशा यानी वामावर्त दिशा में 45° का कोण बनाती है तो प्रवणता (ढ़ाल) का मान tan 45°=1 होगा जबकि x-अक्ष के साथ ऋण दिशा यानी दक्षिणावर्त दिशा में 135° का कोण बनाती है तो रेखा की प्रवणता (m) का \tan 135°=-1 मान होगा।
टिप्पणी: किसी भी रेखा द्वारा x-अक्ष की दिशा से बनाया गया (वामावर्त दिशा में मापा गया) कोण सदैव 0° एवं 180° के मध्य होता है।
(5.)समकोणिक निर्देशाक्ष (Rectangular axes)-
यदि x-अक्ष तथा y-अक्ष को निरूपित करने वाली रेखाएं एक दूसरे पर लंब हो तो उन्हें समकोणिक-निर्देशाक्ष कहते हैं।x-अक्ष या XOX’ रेखा पर सदैव प्रत्येक बिंदु पर कोटि अर्थात् y-निर्देशांक शून्य होता है।अतः x-अक्ष का समीकरण y=0 होता है।y-अक्ष या YOY’ पर सदैव प्रत्येक बिंदु पर भुज अर्थात् x-निर्देशांक शून्य होता है।अतः y-अक्ष का समीकरण x=0 होता है।
(6.)निर्देश अक्षों के समान्तर रेखा का समीकरण (Equation of a Line Parallel to axes)-
(i)x-अक्ष के समान्तर किसी रेखा का समीकरण जो उससे b दूरी पर स्थित है
चित्र के अनुसार माना कि xअक्ष के समान्तर b दूरी पर स्थित कोई रेखा AB है जो कि y-अक्ष की धनात्मक दिशा में M बिंदु पर काटती है।अतः OM=b
माना कि रेखा AB पर कोई चर बिन्दु P(x,y) है।P से x-अक्ष पर लंब PN खींचा अर्थात् P बिंदु के लिए कोटि PN=y परंतु PN=OM
अतः OM=y अर्थात् y=b
इसी प्रकार AB पर स्थित प्रत्येक बिंदु के लिए y-निर्देशांक b के बराबर है।
\therefore AB रेखा का समीकरण y=b है।
उपप्रमेय (Corollary):
(i)यदि रेखा AB,x-अक्ष के नीचे की ओर b दूरी पर हो तो उसका समीकरण y=-b होगा।
(ii)यदि रेखा AB,x-अक्ष से संपाती है तो b=0 होगा।तब AB रेखा का समीकरण और x-अक्ष का समीकरण एक ही y=0 होगा।
(ii)y-अक्ष के समांतर किसी सरल रेखा का समीकरण जो उससे a दूरी पर स्थित है
चित्र के अनुसार माना कि y-अक्ष के समान्तर दूरी पर स्थित कोई रेखा AB है जो कि x-अक्ष की धनात्मक दिशा में N बिन्दु पर काटती है।अतः ON=a
माना कि रेखा AB पर कोई चर बिन्दु P(x,y) है।P से y-अक्ष पर लम्ब PM खींचा अर्थात् P के लिए भुज PM=x परन्तु
PM=ON
अतः ON=x
x=a
इसी प्रकार AB रेखा पर स्थित प्रत्येक बिन्दु के लिए भुज x-निर्देशांक a के बराबर है। अतः रेखा AB का समीकरण x=a होगा।
उपप्रमेय (Corollary):
(i)यदि रेखा AB,y-अक्ष की ऋण दिशा में अर्थात् y-अक्ष के बायीं ओर हो तो उसका समीकरण x=-a होगा।
(ii)यदि रेखा AB,y-अक्ष से संपाती हो तो a=0 होगा। अतः AB रेखा का समीकरण और y-अक्ष का समीकरण एक ही x=0 होगा।
(7.)सरल रेखा का अन्त:खण्ड रूप (Intercept Form of Straight Line)-
अक्षों पर a और b अन्त:खण्ड काटने वाली रेखा का समीकरण:
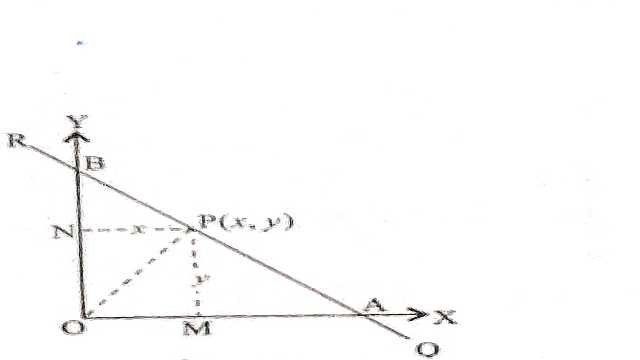
माना कि रेखा QR,x तथा y-अक्षों को क्रमशः A तथा B बिन्दुओं पर इस प्रकार काटती है कि OA=a तथा OB=b. अब AB पर कोई बिन्दु P(x,y) मान लिया।OP को मिलाया और P से x-अक्ष पर PM और y-अक्ष पर PN लम्ब खींचा।
समकोण \triangle OAB का क्षेत्रफल=\triangle OPA का क्षेत्रफल+\triangle OPB का क्षेत्रफल
\frac{1}{2} \times OA \times OB=\frac{1}{2} \times OA \times PM +\frac{1}{2} \times OB \times PN \\ \frac{1}{2} \times a \times b=\frac{1}{2} \times a \times y +\frac{1}{2} \times b \times x
\frac{1}{2} \times a \times b से प्रत्येक पद में भाग देने पर-
अर्थात् \frac{x}{a} +\frac{y}{b} =1
अतः रेखा QR का अभीष्ट समीकरण \frac{x}{a} +\frac{y}{b} =1 है जो कि अन्त:खण्ड रूप कहलाता है।
टिप्पणी:जब a का मान अनन्त की ओर अग्रसर होता है
अर्थात् a \rightarrow \infty तो समीकरण
\frac{x}{\infty} +\frac{y}{b} =1 \Rightarrow \frac{y}{b} =1 \Rightarrow y=b होगी जो
कि x-अक्ष के समान्तर रेखा है।इसी प्रकार b का मान अनन्त की ओर अग्रसर होता है अर्थात् b \rightarrow \infty तो रेखा का समीकरण \frac{x}{a} +\frac{y}{\infty} =1 \Rightarrow \frac{x}{a} =1 \Rightarrow x=a होगी जो कि y-अक्ष के समान्तर रेखा है।
(8.)सरल रेखा का झुकाव रूप या सरल रेखा का स्पर्शज्या रूप (Slope Form of Straight Line)-
y-अक्ष पर C लम्बाई के बराबर अन्त:खण्ड तथा x-अक्ष की धन दिशा से \theta कोण बनाने वाली रेखा का समीकरण
रेखा AB पर कोई बिन्दु P(x,y) लिया।P से OX पर PM लम्ब डाला जो कि मूलबिन्दु O से AB के समान्तर खींची गई रेखा OL को R पर काटती है।
समकोण \triangle OMR में, \tan \theta=\frac{RM}{OM} \\ \Rightarrow RM=OM \tan \theta \\PM=PR+RM (AB \parallel OL)\\ PM=c+OM \tan \theta (ON=RP=c) \\y=x \tan \theta+c \\ \Rightarrow y=mx+c
यहां ,m=\tan \theta रेखा की प्रवणता है।
यही रेखा की अभीष्ट समीकरण है।
टिप्पणी:
(i)यदि रेखा मूलबिन्दु से गुजरती है तब y-अक्ष पर कटा हुआ अन्त:खण्ड शून्य होगा।अतः मूलबिन्दु से गुजरने वाली रेखा का समीकरण y=mx जिसमें C नहीं होगा।
(ii)जब रेखा y-अक्ष को OY पर काटती है तो C का मान धनात्मक एवं OY’ पर काटती है तो C का मान ऋणात्मक होता है।
(iii)जब \theta का मान अधिक कोण हो तो प्रवणता (m) अर्थात् \tan \theta का मान चिन्ह में सदैव धनात्मक होता है।यदि रेखा अक्षों से बराबर कोण बनाती है तब m=\pm 1 होता है।
(9.)सरल रेखा का लम्बरूप (Normal Form of Straight Line)-
मूलबिन्दु से रेखा पर डाले गए लम्ब की लम्बाई तथा लम्ब द्वारा x-अक्ष के साथ बना हुआ कोण दिया हो तो रेखा का समीकरण:
माना कि RS कोई रेखा x-अक्ष एवं y-अक्ष को क्रमशः बिन्दुओं A एवं B पर काटती है।मूलबिन्दु O से रेखा OM लम्ब खींचा जिसकी लम्बाई p तथा यह x-अक्ष की धन दिशा से \alpha कोण बनाता है।अर्थात् \angle MOA=\alpha
समकोण \angle OBM में
\angle OBM= 90^{\circ}-\angle BOM \\=90^{\circ}-(90^{\circ}-\angle MOA) \\=90^{\circ}-(90^{\circ}-\alpha) \\=\alpha
समकोण \angle OMA में
\cos \alpha=\frac{p}{OA} \\\Rightarrow OA=\frac{p}{\cos \alpha}
तथा समकोण \angle OBM में
\sin \alpha=\frac{p}{OB} \\ \Rightarrow OB=\frac{p}{\sin \alpha}
अतः RS रेखा x-अक्ष एवं y-अक्ष पर क्रमशः OA,OB अर्थात् \frac{p}{\cos \alpha},\frac{p}{\sin \alpha} अन्त:खण्ड काटती है।
इसका समीकरण \frac{x}{\frac{p}{\cos \alpha}} +\frac{y}{\frac{p}{\sin \alpha}} =1 \\ \Rightarrow x \cos \alpha+y \sin \alpha=p
यही लम्ब रूप में RS रेखा का समीकरण है।
टिप्पणी:
(i)मूलबिन्दु से रेखा पर डाले गए लम्ब की लम्बाई p सदैव धनात्मक लेते हैं।
(ii)मूलबिन्दु से रेखा पर डाले गए लम्ब द्वारा x-अक्ष की धनात्मक दिशा से बनाया गया कोण का मान 0° से 360° के मध्य कुछ भी सम्भव है।
(iii)किसी भी रेखा का समीकरण ज्ञात करने के लिए दो शर्तो का होना आवश्यक है।
(iv)प्राय: सरल रेखा का समीकरण लिखते समय भुज (x) को पहले तथा कोटि (y) को दूसरे पद पर लिखते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Sum of Series by Difference Method
2.सरल रेखा का समीकरण के उदाहरण (Equation of Straight Lines Examples),सरल रेखा के सवाल और उत्तर (Equation of a Straight line Questions and Answers)-
Example-1.उस सरल रेखा का समीकरण ज्ञात कीजिए जो x-अक्ष के समान्तर है तथा
(i) मूलबिन्दु से ऊपर की ओर 5 इकाई की दूरी पर है।
Solution-x-अक्ष के समान्तर रेखा की प्रवणता m=0
c=5
अतः रेखा का समीकरण y=mx+c
y=0(x)+5
\Rightarrow y=5
(ii)मूलबिन्दु से नीचे की ओर 3 इकाई दूरी पर है।
Solution-x-अक्ष के समान्तर रेखा की प्रवणता m=0 c=-3
अतः रेखा का समीकरण y=mx+c
\Rightarrow y=0(x)-3
\Rightarrow y=-3
Example-2.उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो x-अक्ष के समान्तर है और इससे
(i)x-अक्ष के समान्तर सरल रेखा की प्रवणता m=0
c=a+b
अतः रेखा का समीकरण y=mx+c
y=0(x)+a+b
\Rightarrow y=a+b
(ii)दूरी पर स्थित है
Solution-x-अक्ष के समान्तर रेखा की प्रवणता m=0
y=a^{2}-b^{2}
अतः सरल रेखा की समीकरण y=mx+c
\Rightarrow y=(0)x+a^{2}-b^{2} \\ \Rightarrow y=a^{2}-b^{2}
Example-3.y-अक्ष के समान्तर उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो मूलबिन्दु से क्रमशः
(i)5 इकाई दूरी पर है। (ii)\frac{2}{5} दूरी इकाई दूरी पर स्थित है।
Solution-(i)y-अक्ष के समान्तर किसी रेखा का समीकरण
x=a
\Rightarrow x=5
(ii)x=\frac{2}{5}
\Rightarrow 5x-2= 0
Example-4.उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (-3,2) से होकर जाती है तथा क्रमशः x-अक्ष के लम्बवत् एवं x-अक्ष के समान्तर है।
Solution-x-अक्ष के लम्बवत् रेखा का समीकरण
x=a
यह (-3,2) से गुजरती है
अतः x=-3
x-अक्ष के समान्तर रेखा का समीकरण
y=b
\Rightarrow y=2
Example-5.बिन्दु ( 3,4) से होकर जानेवाली अक्षों के समान्तर रेखाओं के समीकरण ज्ञात कीजिए।इन रेखाओं से 8 इकाई की दूरी पर और इनके समान्तर रेखाओं के समीकरण भी ज्ञात कीजिए।
Solution-x-अक्ष के समान्तर रेखा की समीकरण
y=b
यह (3,4) से गुजरती है अतः y=4
y-अक्ष के समान्तर रेखा की समीकरण
x=a
यह (3,4) से गुजरती है अतः
x=3
इन रेखाओं से 8 इकाई दूरी पर समान्तर रेखाओं की समीकरण-
x=3+8,x=3-8
\Rightarrow x=11,x+5
y=4+8,y=4-8
\Rightarrow y=12,y+4=0
Example-6. x=\pm 4 और y=\pm 3 के प्रतिच्छेद बिन्दुओं के निर्देशांक लिखिए और उनसे निर्मित आयत का क्षेत्रफल भी ज्ञात कीजिए।
Solution– x=\pm 4, y=\pm 3 के प्रतिच्छेद बिन्दु
(4,3),(-4,3),(-4,-3),(4,-3)
आयत का क्षेत्रफल=8×6 वर्ग इकाई
=48 वर्ग इकाई
Example-7.उन रेखाओं के समीकरण ज्ञात कीजिए जो मूलबिन्दु से होकर जाती है तथा
(i)x-अक्ष से -135° का कोण बनाती है।
(ii) प्रथम चतुर्थांश में OY से 60° का कोण बनाती है।
Solution-(i)m=\tan(-135° )\\ =-\tan(135° ) \\ =\tan(180°-45° ) \\=\tan 45° \\ \Rightarrow m=1 \\ c=0
अतः रेखा का समीकरण y=mx+c
y=(x)+0
\Rightarrow x-y=0
(ii)OY से 60° अतः OX से 90°-60=30°
m=\tan 30° \\ \Rightarrow m= \frac{1}{\sqrt {3} } \\ c=0
अतः रेखा का समीकरण y=mx+c
\Rightarrow y= \frac{1}{\sqrt {3} } x+0 \\ \Rightarrow x=-\sqrt{3}y=0
Example-8.उस रेखा का समीकरण ज्ञात कीजिए जो x-अक्ष तथा y-अक्ष पर निम्नलिखित अन्त:खण्ड काटती है
5,3
Solution-a=5,b=3
रेखा का अन्त:खण्ड रूप
\frac{x}{a} +\frac{y}{b} =1 \\ \Rightarrow \frac{x}{5} +\frac{y}{3} =1 \\ \Rightarrow \frac{3x+5y}{15}=1 \\ \Rightarrow 3x+5y=15 \\ \Rightarrow 3x+5y-15=0
Example-9.उस रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (2,3) से गुजरती है तथा अक्षों पर बराबर अन्त:खण्ड काटती है।
Solution-a=b
रेखा का अन्त:खण्ड रूप
\frac{x}{a} +\frac{y}{b} =1 \\ \Rightarrow \frac{x}{a} +\frac{y}{a} =1 \\ \Rightarrow x+y=a
यह (2,3) से गुजरती है अतः
2+3=a
a=5
\Rightarrow x+y=5
Example-10.उस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है रेखा द्वारा x-अक्ष पर काटा गया अन्त:खण्ड y-अक्ष पर काटे गए अन्त:खण्ड का दुगुना है।
Solution-प्रश्नानुसार- a=2b
सरल रेखा का अन्त:खण्ड रूप
\frac{x}{a} +\frac{y}{b} =1 \\ \Rightarrow \frac{x}{2b} +\frac{y}{b} =1 \\ \Rightarrow x+2y=2b
यह (1,2) से गुजरती है अतः
1+(2)(2)=2b
\Rightarrow 1+4=2b \\ \Rightarrow b=\frac{5}{2} \\ \Rightarrow a=2b \\ \Rightarrow a=2 \times \frac{5}{2} \\ \Rightarrow a=5
अतः सरल रेखा का समीकरण
\frac{x}{5} +\frac{y}{\frac{5}{2}} =1 \\ \Rightarrow \frac{x}{5} +\frac{2y}{5} =1 \\ \Rightarrow x+2y=5
Example-11.उस रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (-3,-5) से होकर जाती है तथा दोनों अक्षों के मध्य,रेखा का कटा हुआ अन्त:खण्ड इस बिन्दु पर समद्विभाजित करता है।
Solution-प्रश्नानुसार- x-अक्ष पर प्रतिच्छेद बिन्दु के निर्देशांक (a,0)
y-अक्ष पर प्रतिच्छेद बिन्दु के निर्देशांक (0,b)
\frac{a+0}{2}=-3 ,\frac{0+b}{2}=-5 \\ \Rightarrow a=-6 ,b=-10
रेखा का अन्त:खण्ड रूप
\frac{x}{a} +\frac{y}{b} =1 \\ \Rightarrow \frac{x}{-6} +\frac{y}{-10} =1 \\ \Rightarrow \frac{-5x-3y}{30}=1 \\ \Rightarrow 5x+3y=-30 \\ \Rightarrow 5x+3y+30=0
Example-12.ऐसी दो रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (4,-3) से होकर जाती है तथा अक्षों से काटे हुए अन्त: खण्डों का योग 5 इकाई है।
Solution-a+b=5
b=5-a
रेखाखण्ड का अन्त:खण्ड रूप
\frac{x}{a} +\frac{y}{b} =1 \\ \Rightarrow \frac{x}{a} +\frac{y}{5-a} =1 \\ \Rightarrow (5-a)x+ay=a(5-a)
(4,-3) से होकर जाती है
\Rightarrow (5-a)4+a(-3)=5a-a^{2} \\ \Rightarrow 20-4a-3a=5a-a^{2} \\ \Rightarrow a^{2}-12a+20=0 \\ \Rightarrow a^{2}-10a-2a+20=0 \\ \Rightarrow a(a-10)-2(a-10)=0 \\ \Rightarrow (a-2)(a-10)=0 \\ \Rightarrow a=2,10
जब a=2 तो b=5-a \Rightarrow b=5-2=3
जब a=10 तो b=5-a \Rightarrow b=5-10=-5
अतः रेखाओं के समीकरण
\frac{x}{2} +\frac{y}{3} =1 \\ \Rightarrow 3x+2y=6 \\ \frac{x}{10} -\frac{y}{5} =1 \\ \Rightarrow x-2y=10
Example-13.सिद्ध कीजिए कि उस सरल रेखा का समीकरण जिसके अक्षों पर अन्त: खण्डों के व्युत्क्रम a और b है,ax+by=1 है।
Solution-सरल रेखा का समीकरण
\frac{x}{\frac{1}{a}} +\frac{y}{\frac{1}{b}} =1 \\ \Rightarrow ax+by=1
Example-14.एक सरल रेखा अक्षों से क्रमशः 5 और 3 इकाइयों का अन्त:खण्ड काटती है।इस रेखा का समीकरण ज्ञात कीजिए जबकि अन्त:खण्ड
(i)अक्षों की धन दिशा में हो।(ii)अक्षों की ऋण दिशा में हो।
Solution-(i)जब अन्त:खण्ड अक्षों की धन दिशा में हो
\frac{x}{5} +\frac{y}{3} =1 \\ \Rightarrow 3x+5y=15
(ii)जब अन्त:खण्ड अक्षों की ऋण दिशा में हो
\frac{x}{-5} +\frac{y}{-3} =1 \\ \Rightarrow -3x-5y=15 \\ \Rightarrow 3x+5y+15=0
Example-15.एक सरल रेखा पर मूलबिन्दु से डाला गया लम्ब y-अक्ष से 30° का कोण बनाता है तथा उसकी लम्बाई 2 इकाई है।इस रेखा का समीकरण ज्ञात कीजिए।
Solution–\alpha=90^{\circ}+30^{\circ}=120^{\circ} \\ p=2
अतः रेखा का समीकरण
x \cos \alpha +y \sin \alpha=p \\\Rightarrow x \cos 120^{\circ} +y \sin 120^{\circ}=2 \\ \Rightarrow -\frac{x}{2}+\frac{\sqrt{3}}{2}=2 \\\Rightarrow x-\sqrt{3} y+4=0
Example-16.रेखा x \sin \alpha +y \cos \alpha=\sin 2 \alpha के उस भाग की लम्बाई ज्ञात कीजिए जो अक्षों के मध्य काटता है।इस भाग के मध्य बिन्दु के निर्देशांक ज्ञात कीजिए।
Solution– x \sin \alpha +y \cos \alpha=\sin 2 \alpha
x-अक्ष पर प्रतिच्छेद बिन्दु के निर्देशांक(2 \cos \alpha,0)
y-अक्ष पर प्रतिच्छेद बिन्दु के निर्देशांक (0,2 \sin \alpha )
अक्षों के मध्य भाग की लम्बाई=\sqrt{(2 \cos \alpha-0)^{2}+(0-2 \sin \alpha)^{2}} \\=\sqrt{4(\cos^{2} \alpha+ \sin^{2} \alpha)^{2}} \\ =2
मध्य बिन्दु के निर्देशांक (\cos \alpha,\sin \alpha)
3.सरल रेखा का समीकरण की समस्याएं (Equation of Straight Lines Problems)-
(1.)उस सरल रेखा का समीकरण ज्ञात कीजिए जो y-अक्ष के समान्तर है तथा बिन्दु (4,3) से गुजरती है।
(2.)उस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओं y=8 तथा y=-14 से समान दूरी पर स्थित है।
(3.)उस सरल रेखा का समीकरण ज्ञात कीजिए जो y-अक्ष को मूलबिन्दु से नीचे की ओर 3 इकाई का अन्त:खण्ड काटती है और दोनों अक्षों से बराबर झुकी हुई है।
(4.)उस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (2,3) से होकर जाती है और अक्षों पर बराबर एवं विपरीत चिन्ह के अन्त:खण्ड काटती है।
उत्तर (Answers):(1.)x=4 (2.) y=-3 (3.)x+y+3=0 (4.)x-y+1=0
सरल रेखा का समीकरण (Equation of Straight Lines)में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न 1.आप दो बिंदुओं से एक सरल रेखा के समीकरण को कैसे ज्ञात करेंगे? (How do you find the equation of a straight line from two points?)-
उत्तर:-एक लाइन के समीकरण का पता लगाएं, दो बिंदुओं से गुजरती हैं।एक रेखा का समीकरण आमतौर पर y = mx + b के रूप में लिखा जाता है जहाँ m ढलान है और b, y- अक्ष पर आन्त:खण्ड है।यदि आप दो बिंदुओं को जानते हैं जो एक रेखा से गुजरता है, तो यह पृष्ठ आपको दिखाएगा कि रेखा के समीकरण को कैसे ज्ञात करना है।
दो बिंदुओं से ढलान (या ढाल) का पता लगाएं।इस रेखा का ढलान (या ढाल) क्या है?हम दो बिंदुओं को जानते हैं:चरण 2:”प्वाइंट-स्लोप फॉर्मूला”अब उस ढलान और एक बिंदु को “प्वाइंट-स्लैप फॉर्मूला” में रखें चरण 3.सरल करें।
प्रश्न 2.लम्ब रूप में सरल रेखा का समीकरण क्या है? (What is the equation of straight line in normal form?)-
उत्तर:-(i) x cos α + y sin α = p के रूप में सरल रेखा के समीकरण को उसका लम्ब रूप कहा जाता है।(ii) समीकरण x cos α + y sin α = p में, p का मान हमेशा धनात्मक होता है और 0°≤ α ≤ 360°।
ढलान \frac{A}{B} द्वारा दिया जाता है,यह देखते हुए कि B≠0. · x-इंटरसेप्ट –\frac{C}{A} और y-इंटरसेप्ट द्वारा –\frac{C}{B} दिया जाता है।इसे देखा जा सकता है।
प्रश्न 3.दो बिंदुओं से गुजरने वाली सरल रेखा का समीकरण (Equation of straight line passing through two points)-
उत्तर:-दो बिंदुओं (x_{1},y_{1} )और (x_{2},y_{2}) से गुजरने वाली रेखा का समीकरण y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} (x-x_{1}) है।तो यह दो बिन्दुओं से गजरने वाली सरल रेखा का समीकरण है।
प्रश्न 4.सरल रेखा का सूत्र (Straight Line Formula)-
उत्तर:-सरल रेखा का समीकरण ज्ञात करने के लिए ऊपर तीन सूत्रों का उल्लेख किया गया है जो क्रमशः अन्त:खण्ड रूप,ढाल रूप (स्पर्शज्या रूप) तथा लम्बरूप।
प्रश्न 5.एक बिन्दु के द्वारा आप एक रेखा का समीकरण कैसे ज्ञात करते हैं? (How to find the equation of a line with one point?)-
उत्तर:-एक लाइन के समीकरण का पता लगाएं, जिसे आप लाइन और उसके ढलान पर एक बिंदु जानते हैं।एक सरल रेखा का समीकरण आमतौर पर y = mx + c के रूप में लिखा जाता है, जहाँ m ढलान है और c, y- अन्त:खण्ड है।यदि आपको बिंदु ज्ञात है जिससे कि एक रेखा के माध्यम से गुजरता है, और इसकी ढलान, यह पृष्ठ आपको दिखाएगा कि रेखा के समीकरण को कैसे खोजना है।
Also Read This Article:-Sum of First n Natural Numbers
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |