Lengths of chords of curvature
1.वक्रता जीवाओं की लम्बाईयां का परिचय (Introduction to Lengths of chords of curvature)-
वक्रता जीवाओं की लम्बाईयां ( Lengths of chords of curvature) तीन प्रकार की होती है।
( 1.)मूलबिन्दु (ध्रुव) से होकर जानेवाली वक्रता जीवा की लम्बाई (Length of chord of curvature through origin (pole)।
(2.)ध्रुवान्तर रेखा पर लम्ब वक्रता जीवा की लम्बाई (Length of chord of curvature perpendicular to radius vector)।
(3.)अक्षों के समान्तर वक्रता जीवाओं की लम्बाई (Length of chords of curvature parallel to axes)।
इस आर्टिकल में इन तीनों प्रकार की वक्रता जीवाओं की लम्बाई की थ्योरी को उदाहरणों की सहायता से समझेंगे।इससे पूर्व आर्टिकल में पदिक समीकरणों के लिए वक्रता त्रिज्या,ध्रुवी समुकरणों के लिए वक्रता-त्रिज्या तथा स्पर्शीय ध्रुवी समीकरणों के लिए वक्रता-त्रिज्या व वक्रता-केन्द्र के निर्देशांक के बारे में अध्ययन कर चुके हैं। इसलिए इनका अध्ययन करने के लिए उन आर्टिकल का अध्ययन करना चाहिए।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Radius of curvature for pedal equation
2.वक्रता जीवाओं की लम्बाईयां ( Lengths of chords of curvature)-
(1.)मूलबिन्दु (ध्रुव) से होकर जानेवाली वक्रता जीवा की लम्बाई [(Length of chord of curvature through origin (pole)]-
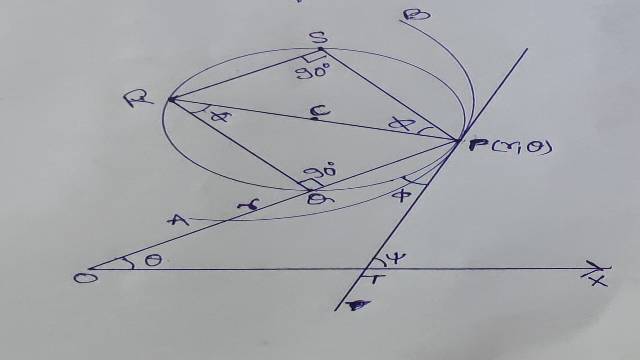
माना कि APB वक्र का एक भाग है और P पर वक्रता-वृत्त PQRS है।PR वक्रता-वृत्त का व्यास है।माना कि PT,P पर स्पर्श रेखा है।P तथा ध्रुव (मूलबिन्दु O) को मिलाएं,तो \angle OPT=\phi ।
माना कि OP वृत्त को Q बिन्दु पर काटता है।
अब \angle PQR=\frac { \pi }{ 2 } (अर्धवृत्त में कोण)
तथा \angle OPR=\frac { \pi }{ 2 } -\phi \Rightarrow \angle QPR=\frac { \pi }{ 2 } -\phi
PR=वक्रता-वृत्त का व्यास=2\rho
\triangle PQRमें
PQ=PR\sin { \theta } \\ =2\rho \sin { \phi }
अतः मूलबिन्दु (ध्रुव) से होकर जानेवाली वक्रता जीवा की लम्बाई [(Length of chord of curvature through origin (pole)]= \rho \sin { \phi } \\ =2\rho .\frac { p }{ r } [\because p=r\sin { \phi } ]
(2.)ध्रुवान्तर रेखा पर लम्ब वक्रता जीवा की लम्बाई (Length of chord of curvature perpendicular to radius vector):
चित्र में हम देखते हैं कि PS,OP पर लम्ब है तथा PR,PT पर लम्ब है।
\angle OPT=\angle RPS=\phi
तथाPS=RP\cos { \phi }
अतः ध्रुवान्तर रेखा पर लम्ब वक्रता जीवा की लम्बाई (Length of chord of curvature perpendicular to radius vector)==2\rho \cos { \phi } \\ =2\rho \sqrt { 1-\sin ^{ 2 }{ \phi } } \\ =2\rho \sqrt { 1-\frac { { p }^{ 2 } }{ { r }^{ 2 } } } \\ =\frac { 2\rho }{ r } \sqrt { { r }^{ 2 }-{ p }^{ 2 } }
(3.)अक्षों के समान्तर वक्रता जीवाओं की लम्बाई (Length of chords of curvature parallel to axes):
माना वक्र पर कोई बिन्दु P है तथा P पर वक्रता केन्द्र C पर तथा P पर स्पर्श रेखा x-अक्ष के साथ कोण बनाती है।
P से PA,x-अक्ष के समान्तर तथा PB ,y-अक्ष के समान्तर वक्रता-वृत्त की जीवा खींचिए।
अब ज्यामिति से
\angle BPR=\angle PTX=\psi \\ \angle RPA=\frac { \pi }{ 2 } -\psi तथा PR=2\rho
समकोण त्रिभुज PAR से,
PA =x-अक्ष के समान्तर वक्रता जीवा की लम्बाई=
PA=PR\cos { (\frac { \pi }{ 2 } -\psi ) } \\ =2\rho \sin { \psi }
तथा समकोण त्रिभुज PBR से,
PB=y-अक्ष के समान्तर वक्रता जीवा की लम्बाई
3.वक्रता जीवाओं की लम्बाईयां के उदाहरण ( Lengths of chords of curvature Examples)-
Example-1.वक्र{ r }^{ n }={ a }^{ n }\cos { n\theta } के किसी बिन्दु P पर वक्रता-वृत्त ध्रुवान्तर रेखा OP को A पर काटता है।यदि ध्रुव O हो तो सिद्ध कीजिए कि
(The circle of curvature at any time P of the curve { r }^{ n }={ a }^{ n }\cos { n\theta } meets the radius vector OP at A.If O is the pole,prove that OP:AP=(n+1):2
जब (when) n=2 तो (then) सिद्ध कीजिए कि (Prove that)
OP:AP=3:2
Solution-{ r }^{ n }={ a }^{ n }\cos { n\theta } …(1)
दोनों पक्षों का लघुगुणक लेने पर-
n\log { r } =n\log { a } +\log { \cos { n\theta } }
\theta के सापेक्ष अवकलन करने पर-
\Rightarrow \frac { n }{ r } .\frac { dr }{ d\theta } =0+\frac { 1 }{ \cos { n\theta } } .(-n\sin { n\theta } )\\ \Rightarrow \frac { dr }{ d\theta } =-r\frac { \sin { n\theta } }{ \cos { n\theta } } \\ \Rightarrow \frac { dr }{ d\theta } =-r\tan { n\theta } \\ \tan { \phi } =r\frac { d\theta }{ dr } \\ \Rightarrow \tan { \phi } =r(-\frac { 1 }{ r } \cot { n\theta } )\\ \Rightarrow \tan { \phi } =-\cot { n\theta } \\ \Rightarrow \tan { \phi } =\tan { (\frac { \pi }{ 2 } +n\theta ) } \\ \Rightarrow \phi =\frac { \pi }{ 2 } +n\theta ................(2)\\ p=rsin{ \phi }\\ p=rsin{ (\frac { \pi }{ 2 } +n\theta ) }\\ p=rcos{ n\theta }\Rightarrow p=r(\frac { { r }^{ n } }{ { a }^{ n } } )=\frac { { r }^{ n+1 } }{ { a }^{ n } }
r के सापेक्ष अवकलन करने पर-
\Rightarrow \frac { dp }{ dr } =\frac { (n+1){ r }^{ n } }{ { a }^{ n } } \\ \rho =r\frac { dr }{ dp } \\ \Rightarrow \rho =r.\frac { 1 }{ \frac { (n+1){ r }^{ n } }{ { a }^{ n } } } .........(3)\\ \Rightarrow \rho =r\times \frac { { a }^{ n } }{ (n+1){ r }^{ n } } \\ \Rightarrow \rho =\frac { { a }^{ n } }{ (n+1){ r }^{ n-1 } }
मूलबिन्दु (ध्रुव) से होकर जानेवाली वक्रता जीवा की लम्बाई [(Length of chord of curvature through origin (pole)]=
cos{ n\theta } का मान (1) से रखने पर-
\Rightarrow PA=2\frac { { a }^{ n } }{ (n+1){ r }^{ n-1 } } .\frac { { r }^{ n } }{ { a }^{ n } } \\ \Rightarrow PA=\frac { 2r }{ (n+1) } \\ OP:AP=r:\frac { 2r }{ (n+1) } \\ \Rightarrow OP:AP=(n+1):2
n=2 रखने पर-
OP:AP=3:2
Example-2.सिद्ध कीजिए कि कैटिनरी y=c\cosh { \left( \frac { x }{ c } \right) } के लिए y-अक्ष के समान्तर वक्रता-जीवा कोटि की दुगुनी होती है एवं x-अक्ष के समान्तर वक्रता-जीवा की लम्बाई\sinh { \left( \frac { x }{ c } \right) } होती है।
(Show that the chord on curvature parallel to y-axis for the catenaryy=c\cosh { \left( \frac { x }{ c } \right) } is double of the ordinate,whereas the chord parallel to x-axis is of length \sinh { \left( \frac { x }{ c } \right) } .)
Solution-y=c\cosh { \left( \frac { x }{ c } \right) }
x-अक्ष के सापेक्ष समाकलन करने पर-
{ y }_{ 1 }=\frac { dy }{ dx } =\sinh { \left( \frac { x }{ c } \right) }
पुनः x के सापेक्ष समाकलन करने पर-
{ y }_{ 2 }=\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =\frac { 1 }{ c } \cosh { \left( \frac { x }{ c } \right) } \\ \rho =\frac { { \left( 1+{ y }_{ 1 }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { y }_{ 2 } } \\ \Rightarrow \rho =\frac { { \left( 1+\sinh ^{ 2 }{ \left( \frac { x }{ c } \right) } \right) }^{ \frac { 3 }{ 2 } } }{ \frac { 1 }{ c } \cosh { \left( \frac { x }{ c } \right) } } \\ \Rightarrow \rho =\frac { { \left( \cosh ^{ 2 }{ \left( \frac { x }{ c } \right) } \right) }^{ \frac { 3 }{ 2 } } }{ \frac { 1 }{ c } \cosh { \left( \frac { x }{ c } \right) } } \\ \Rightarrow \rho =\frac { c\cosh ^{ 3 }{ \left( \frac { x }{ c } \right) } }{ \cosh { \left( \frac { x }{ c } \right) } } \\ \Rightarrow \rho =\cosh ^{ 2 }{ \left( \frac { x }{ c } \right) } ..........(1)\\ \frac { dy }{ dx } =\tan { \psi } \\ \Rightarrow \tan { \psi } =\sinh { \left( \frac { x }{ c } \right) }
कर्ण=\sqrt { 1+\sinh ^{ 2 }{ \left( \frac { x }{ c } \right) } } \\ =\sqrt { \cosh ^{ 2 }{ \left( \frac { x }{ c } \right) } } \\ =\cosh { \left( \frac { x }{ c } \right) } \\ \Rightarrow sin{ \psi }=\frac { \sinh { \left( \frac { x }{ c } \right) } }{ \cosh { \left( \frac { x }{ c } \right) } } ......(2)\\ \Rightarrow \cos { \psi } =\frac { 1 }{ \cosh { \left( \frac { x }{ c } \right) } } .......(3)
x-अक्ष के समान्तर वक्रता जीवा की लम्बाई= 2\rho \sin { \psi } \\ =2c\cosh ^{ 2 }{ \left( \frac { x }{ c } \right) } .\frac { \sinh { \left( \frac { x }{ c } \right) } }{ \cosh { \left( \frac { x }{ c } \right) } } \\ =2c\cosh { \left( \frac { x }{ c } \right) } \sinh { \left( \frac { x }{ c } \right) } \\ =c\sinh { \left( \frac { 2x }{ c } \right) }
y-अक्ष के समान्तर वक्रता जीवा की लम्बाई= 2\rho \cos { \psi } \\ =2c\cosh ^{ 2 }{ \left( \frac { x }{ c } \right) } .\frac { 1 }{ \cosh { \left( \frac { x }{ c } \right) } } \\ =2c\cosh { \left( \frac { x }{ c } \right) } \\ =2y
Example-3.सिद्ध कीजिए कि लेमनीसकेट { r }^{ 2 }={ a }^{ 2 }\cos { 2\theta } के ध्रुव से गुजरने वाली जीवा(\frac { 2 }{ 3 } )r है।
(Show that the chord of curvature through the pole of the lemniscate{ r }^{ 2 }={ a }^{ 2 }\cos { 2\theta } is(\frac { 2 }{ 3 } )r.)
Solution–{ r }^{ 2 }={ a }^{ 2 }\cos { 2\theta } .........(1)
दोनों पक्षों का लघुगुणक लेने पर-
\theta के सापेक्ष अवकलन करने पर-
\frac { 2 }{ r } .\frac { dr }{ d\theta } =0+\frac { 1 }{ \cos { 2\theta } } (-2\sin { 2\theta } )\\ \Rightarrow \frac { 1 }{ r } .\frac { dr }{ d\theta } =-\frac { \sin { 2\theta } }{ \cos { 2\theta } } \\ \Rightarrow \frac { dr }{ d\theta } =-r\tan { 2\theta } \\ \tan { \phi } =r\frac { d\theta }{ dr } \\ \Rightarrow \tan { \phi } =r(-\frac { 1 }{ r } \cot { 2\theta } )\\ \Rightarrow \tan { \phi } =-\cot { 2\theta } \\ \Rightarrow \tan { \phi } =\tan { \left( \frac { \pi }{ 2 } +2\theta \right) } \\ \Rightarrow \phi =\frac { \pi }{ 2 } +2\theta .........(2)\\ p=r\sin { \phi } \\ \Rightarrow p=r\sin { (\frac { \pi }{ 2 } +2\theta ) } \\ \Rightarrow p=r\cos { 2\theta } \\ \Rightarrow p=r.\frac { { r }^{ 2 } }{ { a }^{ 2 } } [(2) से ]
\Rightarrow p=\frac { { r }^{ 3 } }{ { a }^{ 2 } }
r के सापेक्ष अवकलन करने पर-
\frac { dp }{ dr } =\frac { { 3r }^{ 2 } }{ { a }^{ 2 } } \\ \rho =r\frac { dr }{ dp } \\ \Rightarrow \rho =r(\frac { { a }^{ 2 } }{ 3{ r }^{ 2 } } )\\ \Rightarrow \rho =\frac { { a }^{ 2 } }{ 3r }
अतः मूलबिन्दु (ध्रुव) से होकर जानेवाली वक्रता जीवा की लम्बाई [(Length of chord of curvature through origin (pole)]= 2\rho \sin { \phi } \\ =\frac { { 2a }^{ 2 } }{ 3r } .\cos { 2\theta } \\ =\frac { { 2a }^{ 2 } }{ 3r } .\frac { { r }^{ 2 } }{ { a }^{ 2 } } [(1) से ]
=\frac { 2 }{ 3 } r
Example-4.सिद्ध कीजिए कि समान कोणिक सर्पिल r=a{ e }^{ m\theta }की ध्रुव से जानेवाली वक्रता-जीवा की लम्बाई 2r है।
(Show that the chord of curvature, through the pole of the equiangular spiralr=a{ e }^{ m\theta } is 2r.)
Solution–r=a{ e }^{ m\theta }
\theta के सापेक्ष अवकलन करने पर-
कर्ण= \sqrt { 1+{ m }^{ 2 } } \\ \Rightarrow \sin { \phi } =\frac { 1 }{ \sqrt { 1+{ m }^{ 2 } } } \\ p=r\sin { \phi } \\ p=r\frac { 1 }{ \sqrt { 1+{ m }^{ 2 } } }
r के सापेक्ष अवकलन करने पर-
\Rightarrow \frac { dp }{ dr } =\frac { 1 }{ \sqrt { 1+{ m }^{ 2 } } } \\ \rho =r\frac { dr }{ dp } \\ \Rightarrow \rho =r.\sqrt { 1+{ m }^{ 2 } }
मूलबिन्दु (ध्रुव) से होकर जानेवाली वक्रता जीवा की लम्बाई [(Length of chord of curvature through origin (pole)]= 2\rho \sin { \phi } \\ =2r\sqrt { 1+{ m }^{ 2 } } .\frac { 1 }{ \sqrt { 1+{ m }^{ 2 } } }
=2r
उपर्युक्त उदाहरणों के हल द्वारा वक्रता जीवाओं की लम्बाईयां ( Lengths of chords of curvature) को समझा जा सकता है।
Also Read This Article:-Radius of curvature for polar equation
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |