Menu

Radius of curvature for pedal equation

August 29, 2020 Differential Calculus No Comments
Contents hide
1 1.पदिक समीकरण के लिए वक्रता त्रिज्या का परिचय (Introduction to Radius of curvature for pedal equation)-
1.1 2.पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for pedal equation)-
1.2 3.स्पर्शीय ध्रुवी समीकरणों के लिए वक्रता त्रिज्या (Formula for radius of curvature for tangential polar equation)-
1.2.1 4.पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for polar equation) पर आधारित सवाल-
1.2.2 5.स्पर्शीय ध्रुवी समीकरणों के लिए वक्रता त्रिज्या ( Radius of curvature for tangential pedal equation) पर आधारित सवाल-

1.पदिक समीकरण के लिए वक्रता त्रिज्या का परिचय (Introduction to Radius of curvature for pedal equation)-

पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for pedal equation) ज्ञात करने के लिए सर्वप्रथम पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for pedal equation) का सूत्र स्थापित करेंगे।इसके पश्चात् स्पर्शीय धुर्वी समीकरणों के लिए वक्रता त्रिज्या सूत्र स्थापित करेंगे।इस आर्टिकल से पूर्व हमने वक्रता त्रिज्या के लिए कार्तीय सूत्र तथा प्राचलिक वक्रों की वक्रता त्रिज्या से सम्बन्धित आर्टिकल पोस्ट किया था। इसलिए इस आर्टिकल को पढ़ने से पहले उन आर्टिकल का अध्ययन करना चाहिए।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Perpendicular length pole on tangent

2.पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for pedal equation)-

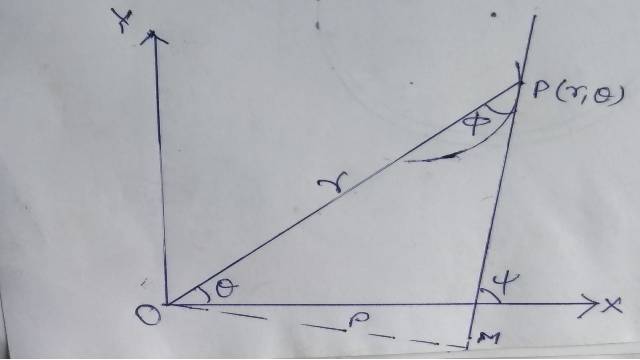
मान लो मूलबिन्दु से,वक्र के बिन्दु P(r,\theta ) पर स्पर्श रेखा पर डाले गए लम्ब (perpendicular) की लम्बाई p है,तब p व r में किसी सम्बन्ध को पदिक समीकरण (pedal equation) कहते हैं।बिन्दु P के पदिक निर्देशांक (pedal coordinates) कहलाते हैं।

मान लो वक्र का पदिक समीकरण है
p=f(r)
जैसा कि चित्र से स्पष्ट है कि \theta ,\phi तथा \psi का सम्बन्ध निम्न प्रकार है-

\psi =\theta +\phi …..(1)
\frac { 1 }{ \rho } =\frac { d\psi }{ ds } =\frac { d\theta }{ ds } +\frac { d\phi }{ ds } [(1) से]

\Rightarrow \frac { 1 }{ \rho } =\frac { d\theta }{ ds } +\frac { d\phi }{ dr } .\frac { dr }{ ds } \\ =\frac { 1 }{ r } \sin { \phi } +\cos { \phi } \frac { d\phi }{ dr }

=\frac { 1 }{ r } .\left[ \sin { \phi } .1+\cos { \phi } \frac { d\phi }{ dr } \right] [ \because \sin { \phi } =r\frac { d\theta }{ ds } तथा \cos { \phi } =\frac { dr }{ ds } ]

=\frac { 1 }{ r } .\frac { d }{ dr } (r\sin { \phi } )\\ =\frac { 1 }{ r } .\frac { dp }{ dr } \quad \quad [\because p=r\sin { \phi } ]\\ \Rightarrow \rho =r.\frac { dr }{ dp }

3.स्पर्शीय ध्रुवी समीकरणों के लिए वक्रता त्रिज्या (Formula for radius of curvature for tangential polar equation)-

\frac { dr }{ ds } =\cos { \phi }

तथा \rho =\frac { ds }{ d\psi }=r\frac { dr }{ dp } ,\rho =r\sin { \phi }
अब \frac { dp }{ d\psi } =\frac { dp }{ dr } .\frac { dr }{ ds } .\frac { ds }{ d\psi } \\ =\frac { dp }{ dr } .\cos { \phi } .(r\frac { d\phi }{ dp } )
या \frac { dp }{ d\psi } =r\cos { \phi }
अब { (r\cos { \phi } ) }^{ 2 }+{ (r\sin { \phi } ) }^{ 2 }={ \left( \frac { dp }{ d\psi } \right) }^{ 2 }+{ p }^{ 2 }\\ \Rightarrow { r }^{ 2 }={ p }^{ 2 }+{ \left( \frac { dp }{ d\psi } \right) }^{ 2 }
दोनों पक्षों का p के सापेक्ष अवकलन करने पर-

2r\frac { dr }{ dp } =2p+2(\frac { dp }{ d\psi } )\frac { d }{ d\psi } (\frac { dp }{ d\psi } )(\frac { d\psi }{ dp } )\\ \Rightarrow r\frac { dr }{ dp } =p+\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } }

अतः \rho =p+\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } }

4.पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for polar equation) पर आधारित सवाल-

Question-1.{ r }^{ 3 }=2a{ p }^{ 2 }(कार्डिआयड)
Solution- { r }^{ 3 }=2a{ p }^{ 2 }

p के सापेक्ष अवकलन करने पर-

3{ r }^{ 2 }\frac { dr }{ dp } =4ap\\ \Rightarrow \frac { dr }{ dp } =\frac { 4ap }{ 3{ r }^{ 2 } } \\ \Rightarrow \rho =r\frac { dr }{ dp } \\ \Rightarrow \rho =r.\frac { 4ap }{ 3{ r }^{ 2 } } \\ \Rightarrow \rho =\frac { 4ap }{ 3{ r } } \\ \Rightarrow \rho =\frac { 4a }{ 3{ r } } .\frac { { r }^{ \frac { 3 }{ 2 } } }{ ({ 2a) }^{ \frac { 1 }{ 2 } } } \\ \Rightarrow \rho =\frac { 2\sqrt { 2 } \sqrt { ar } }{ 3 } \\ \Rightarrow \rho =\frac { 2\sqrt { 2ar } }{ 3 }

Question-2.{ p }^{ 2 }=ar
Solution-{ p }^{ 2 }=ar
p के सापेक्ष अवकलन करने पर-

2p=a\frac { dr }{ dp } \\ \Rightarrow \rho =r\frac { dr }{ dp } \\ \Rightarrow \rho =\frac { { p }^{ 2 } }{ a } (\frac { 2p }{ a } )\\ \Rightarrow \rho =\frac { 2{ p }^{ 3 } }{ { a }^{ 2 } }

5.स्पर्शीय ध्रुवी समीकरणों के लिए वक्रता त्रिज्या ( Radius of curvature for tangential pedal equation) पर आधारित सवाल-

Question-3.{ p }^{ 2 }={ a }^{ 2 }\cos ^{ 2 }{ \psi +{ b }^{ 2 } } \sin ^{ 2 }{ \psi }

Solution:-{ p }^{ 2 }={ a }^{ 2 }\cos ^{ 2 }{ \psi +{ b }^{ 2 } } \sin ^{ 2 }{ \psi } ..(1)

\psi   के सापेक्ष अवकलन करने पर-

2p\frac { dp }{ d\psi } =-2{ a }^{ 2 }\cos { \psi } \sin { \psi } +2{ b }^{ 2 }\sin { \psi } \cos { \psi } \\ p\frac { dp }{ d\psi } =-{ a }^{ 2 }\cos { \psi } \sin { \psi } +{ b }^{ 2 }\sin { \psi } \cos { \psi }
पुनः समीकरण (2) का \psi के सापेक्ष अवकलन करने पर-

p\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } +{ \left( \frac { dp }{ d\psi } \right) }^{ 2 }={ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi }
का मान समीकरण (2) से समीकरण (3) में रखने पर-

p\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } +{ \left( \frac { -{ a }^{ 2 }\cos { \psi } \sin { \psi } +{ b }^{ 2 }\sin { \psi } \cos { \psi } }{ p } \right) }^{ 2 }={ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } \\ p\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } +\frac { { a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } +{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } -2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } }{ { p }^{ 2 } } ={ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } \\ p\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } =\frac { -{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } }{ { p }^{ 2 } } +{ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } \\ \frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } =\frac { -{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } }{ { p }^{ 3 } } +\frac { { a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } }{ p } \\ \rho =p+\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } \\ \rho =p+\frac { -{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } }{ { p }^{ 3 } } +\frac { { a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } }{ p } \\ \rho =\frac { \begin{matrix} { p }^{ 4 }-{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \\ +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \\ +{ p }^{ 2 }({ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } ) \end{matrix} }{ { p }^{ 3 } } \\ \rho =\frac { \begin{matrix} { p }^{ 2 }[{ p }^{ 2 }+{ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } ] \\ -{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \\ +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \end{matrix} }{ { p }^{ 3 } } \\ \rho =\frac { \begin{matrix} { p }^{ 2 }[{ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\sin ^{ 2 }{ \psi } +{ a }^{ 2 }\sin ^{ 2 }{ \psi } -{ a }^{ 2 }\cos ^{ 2 }{ \psi } \\ +{ b }^{ 2 }\cos ^{ 2 }{ \psi } -{ b }^{ 2 }\sin ^{ 2 }{ \psi } ]-{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } \\ -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \end{matrix} }{ { p }^{ 3 } } \\ \rho =\frac { \begin{matrix} { p }^{ 2 }[{ a }^{ 2 }\sin ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } ]-{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } \\ -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \end{matrix} }{ { p }^{ 3 } } \\ \rho =\frac { \begin{matrix} ({ a }^{ 2 }\cos ^{ 2 }{ \psi } +{ b }^{ 2 }\sin ^{ 2 }{ \psi } )({ a }^{ 2 }\sin ^{ 2 }{ \psi } +{ b }^{ 2 }\cos ^{ 2 }{ \psi } ) \\ -{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \\ +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \end{matrix} }{ { p }^{ 3 } } \\ \rho =\frac { \begin{matrix} { a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } +{ a }^{ 2 }{ b }^{ 2 }\cos ^{ 4 }{ \psi +{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 4 }{ \psi } } \\ +{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } -{ a }^{ 4 }\cos ^{ 2 }{ \psi } \sin ^{ 2 }{ \psi } \\ -{ b }^{ 4 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } +2{ a }^{ 2 }{ b }^{ 2 }\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } \end{matrix} }{ { p }^{ 3 } } \\ \rho =\frac { { a }^{ 2 }{ b }^{ 2 }(\cos ^{ 4 }{ \psi +\sin ^{ 4 }{ \psi } } +2\sin ^{ 2 }{ \psi } \cos ^{ 2 }{ \psi } ) }{ { p }^{ 3 } } \\ \rho =\frac { { a }^{ 2 }{ b }^{ 2 }{ (\cos ^{ 2 }{ \psi } +\sin ^{ 2 }{ \psi } ) }^{ 2 } }{ { p }^{ 3 } } \\ \rho =\frac { { a }^{ 2 }{ b }^{ 2 } }{ { p }^{ 3 } }  

Question-4.p=asin{ b\psi } {दीर्घवृत }

Solution:-p=asin{ b\psi }

\psi के सापेक्ष अवकलन करने पर-

\frac { dp }{ d\psi } =abcos{ b\psi }....(1)
पुनः समीकरण (1) का \psi के सापेक्ष अवकलन करने पर-

\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } =-a{ b }^{ 2 }sin{ b\psi }\\ \rho =p+\frac { { d }^{ 2 }p }{ d{ \psi }^{ 2 } } \\ \Rightarrow \rho =p-a{ b }^{ 2 }sin{ b\psi }\\ \Rightarrow \rho =p-{ b }^{ 2 }p\\ \Rightarrow \rho =p(1-{ b }^{ 2 })

इस प्रकार उपर्युक्त सवालों के हल द्वारा पदिक समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for pedal equation) को समझा जा सकता है।

Also Read This Article:-Radius of curvature for polar equation

No. Social Media Url
1. Facebook click here
2. you tube click here
3. Twitter click here
4. Instagram click here
5. Linkedin click here
6. Facebook Page click here

Related Posts

About Author

Satyam

About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.

Leave a Reply

Your email address will not be published. Required fields are marked *