Complex Numbers
1.सम्मिश्र संख्याएं (Complex Numbers), सम्मिश्र संख्याओं का कोणांक (Complex Numbers Argument):
सम्मिश्र संख्याएं (Complex Numbers):जैन गणितज्ञ महावीराचार्य ने 850 ई. में यह संकेत दिया कि ऋणात्मक संख्याओं के वर्गमूल नहीं होते।1637 ई. में रेने डिकार्टिज ने संख्याओं को वास्तविक व काल्पनिक नाम दिए।आयलर ने 1748 ई. में काल्पनिक संख्याओं के लिए i का प्रयोग किया।गाॅउस ने सर्वप्रथम 1832 में सम्मिश्र संख्याओं को वास्तविक और काल्पनिक भागों में व्यक्त किया और a+ib को सम्मिश्र संख्या कहा।
द्विघात समीकरण ax^{2}+bx+c=0 के वास्तविक हल मानक सूत्र से प्राप्त करते हैं। इसमें यदि विविक्तिकर b^{2}-4ac\geq 0 हो तो हल वास्तविक प्राप्त होते हैं परन्तु विविक्तिकर b^{2}-4ac < 0 की स्थिति में हम उपर्युक्त समीकरण के वास्तविक हल निकालने में असमर्थ हैं।क्योंकि इस स्थिति में एक ऋणात्मक संख्या का वर्गमूल एक वास्तविक संख्या नहीं है।इस प्रकार की समस्या का समाधान करने हेतु वास्तविक संख्या प्रणाली का विस्तार कर एक ऐसी संख्या प्रणाली विकसित की गई जिसमें ऋणात्मक संख्याओं के वर्गमूल भी सम्मिलित हैं।ऐसी संख्याएं सम्मिश्र संख्याएं (Complex Numbers) कहलाती हैं।
समान चिन्ह वाली दो वास्तविक संख्याओं का गुणनफल धनात्मक होता है किन्तु यदि \sqrt{-1} को \sqrt{-1} से गुणा करें तो गुणनफल ऋणात्मक आता है।गणितज्ञों ने ऐसी संख्याओं को काल्पनिक संख्याएं (Imaginary Quantities) कहा है।
सम्मिश्रण संख्या की परिभाषा(Definition of Complex Number):उस प्रत्येक संख्या को जिसका वर्ग ऋणात्मक संख्या हो,अधिकल्पित या काल्पनिक संख्या कहते हैं।
यदि a,b \in R तो a+ib या a-ib रूप वाले व्यंजक सम्मिश्र संख्याएं (Complex Numbers) कहलाती हैं। जिसे प्रायः z से व्यक्त किया जाता है यथा z=a+ib जहां i=\sqrt{-1} (मानक रूप); यहां a वास्तविक भाग तथा b काल्पनिक भाग कहलाता है।
क्रमित युग्म में सम्मिश्र राशि (Complex Number in Ordered pair): हेमिल्टन (1805-1865) ने सम्मिश्र राशि को एक क्रमित युग्म के रूप में परिभाषित किया जिसके अनुसार सम्मिश्र राशि (Complex Numbers) z=a+ib को (a,b) से निरूपित किया जाता है जहां a,b \in R सम्मिश्र राशि (Complex Numbers) के वास्तविक व काल्पनिक भाग को क्रमशः Re(z) और Im(z) से व्यक्त करते हैं।
सम्मिश्र संख्याओं पर प्रमेय (Theorem on Complex Numbers):
प्रमेय (Theorem):1.यदि कोई सम्मिश्र संख्या शून्य के बराबर हो तो उसके वास्तविक और काल्पनिक दोनों भाग शून्य के बराबर होते हैं।
प्रमेय (Theorem):2.यदि दो सम्मिश्र संख्याएं बराबर हो तो उनके वास्तविक और काल्पनिक भाग अलग-अलग बराबर होते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Equation of Straight Line
2.सम्मिश्र संख्याओं के उदाहरण (Complex Numbers Examples):
Example:1.-2 का मुख्य कोणांक लिखिए।
Solution:-2+i.0
a=-2,b=0
कोणांक (Argument) \theta=\pi-\tan^{-1} \left|\frac{b}{a}\right| \\ =\pi-\tan^{-1} \left|\frac{0}{-2}\right| \\ =\pi-\tan ^{-1} 0
कोणांक (Argument) \theta=\pi
Example:2.\frac{5 \sqrt{3}}{2}+\frac{5 i}{2} का ध्रुवीय रूप लिखिए।
Solution:- \frac{5 \sqrt{3}}{2}+\frac{5 i}{2}
माना \frac{5 \sqrt{3}}{2}+\frac{5}{2} i=r \cos \theta+i r \sin \theta \\ \Rightarrow r \cos \theta=\frac{5 \sqrt{3}}{2}
तथा r \sin \theta=\frac{5}{2}
वर्ग करके जोड़ने पर-
r^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)=\left(\frac{5 \sqrt{3}}{2}\right)^{2}+\left(\frac{5}{2}\right)^{2} \\ \Rightarrow r^{2}=\frac{75}{4}+\frac{25}{4} \\ \Rightarrow r^{2}=25 \\ \Rightarrow r=5 \\ a=\frac{5 \sqrt{3}}{2}, b=\frac{5}{2} \\ \theta=\tan ^{-1}\left|\frac{b}{a}\right| \\ =\tan ^{-1}\left|\frac{\frac{5}{2}}{\frac{5 \sqrt{3}}{2}}\right| \\ =\tan^{-1} \left|\frac{1}{\sqrt{3}}\right| \\ \theta=\frac{\pi}{6}
अतः r (cos \theta+i \sin \theta)=5(\cos \frac{\pi}{6} +i \sin \frac{\pi}{6})
Example:3.4+5 \omega^{4}+3 \omega^{5} का मान होगा?
Solution:4+5 \omega^{4}+3 \omega^{5} \\ 4+5 \omega+3 \omega^{2} \quad\left(\therefore \omega^{3} =1 \right) \\ \Rightarrow 4+2 w+3 w+3 w^{2} \\ \Rightarrow 4+2 w+3\left(w+w^{2}\right) \\ \Rightarrow 4+2 w+3(-1) \quad\left[\because 1+w+\omega^{2}=0\right] \\ \Rightarrow 1+2 \omega \\ \Rightarrow 1+2\left(\frac{-1+i \sqrt{3}}{2}\right) \quad\left[\therefore \omega=\frac{-1+i \sqrt{3}}{2}\right] \\ \Rightarrow 1-1+i \sqrt{3} \\ \Rightarrow \sqrt{3} i
Example:4.\frac{1}{(1-\cos \theta+i \sin \theta)} को a+ib के रूप में लिखिए।
Solution: \frac{1}{(1-\cos \theta+i \sin \theta)} \\ =\frac{1}{(1-\cos \theta)+i (\sin \theta)} \\ =\frac{1}{2 \sin ^{2} \frac{\theta}{2}+2 i \sin \frac{\theta}{2} \cos \frac{\theta}{2}} \\ =\frac{1}{2 \sin \frac{\theta}{2} (\sin \frac{\theta}{2} +i \cos \frac{\theta}{2})} \times \frac{\sin \frac{\theta}{2}-i \cos \frac{\theta}{2}}{\sin \frac{\theta}{2}-i \cos \frac{\theta}{2}} \\ =\frac{\sin \frac{\theta}{2}-i \cos \frac{\theta}{2}}{2 \sin \frac{\theta}{2} \left(\sin ^{2} \frac{\theta}{2}+\cos ^{2} \frac{\theta}{2} \right)} \\ =\frac{\sin \frac{\theta}{2}(1-i \cot \frac{\theta}{2})}{2 \sin \frac{\theta}{2}} \\ =\frac{1}{2}-\frac{i}{2} \cot \frac{\theta}{2}
Example:5. |1-i|^{x}=2^{x} के शून्येत्तर पूर्णांक मूलों की संख्या है:
Solution:-|1-i|^{x}=2^{x} \\ \Rightarrow\left[\sqrt{(1)^{2}+(-1)^{2}}\right]^{x}=2^{x} \\ \Rightarrow (\sqrt{2})^{x}=2^{x} \\ \Rightarrow 2^{\frac{x}{2}}=2^{x} \\ \Rightarrow \frac{x}{2}=x \Rightarrow \frac{x}{2}=0 \\ \Rightarrow x=0
शून्येत्तर पूर्णांक मूल नहीं है।
Example:6.यदि \left|z_{1}\right|=1=\left|z_{2}\right| तो सिद्ध कीजिए
\left|z_{1}+z_{2}\right|=\left|\frac{1}{z_{1}}+\frac{1}{z_{2}}\right|
Solution: L.H.S. \left|z_{1}+z_{2}\right| =\left|z_{1}\right|+\left|z_{2}\right| \\ =1+1 \\ \left|z_{1}+z_{2}\right| =2
R.H.S \left|\frac{1}{z_{1}}+\frac{1}{z_{2}}\right| =\left|\frac{1}{z_{1}}\right|+\left|\frac{1}{z_{2}}\right| \\ =\frac{1}{\left|z_{1}\right|}+\frac{1}{\left|z_{2}\right|} \\ =\frac{1}{1}+\frac{1}{1} \\ =2
अतः \left|z_{1}+z_{2}\right|+\left|\frac{1}{z_{1}}+\frac{1}{z_{2}}\right|
Example:7.यदि \frac{(-a+i)^{2}}{2 a-i}=p+i q तो सिद्ध कीजिए कि p^{2}+q^{2}=\frac{\left(a^{2}+1\right)^{2}}{4 a^{2}+1}
Solution:\frac{(a+i)^{2}}{2 a-i}-p+i q \\ \Rightarrow \frac{(a+i)^{2}(2 a+i)=p+i a}{(2 a-i)(2 a+i)} \\ \Rightarrow \frac{(a+i)(2 a^{2}+a i+2 a i+i^{2})}{4 a^{2}-i^{2}}=p+i q \\ \Rightarrow \frac{(a+i)\left(2 a^{2}+3 a i-1\right)}{4 a^{2}+1}=p+i q \\ \Rightarrow \frac{\left(2 a^{3}-4 a\right)+i\left(5 a^{2}-1\right)}{4 a^{2}+1}=p+i q
वास्तविक और काल्पनिक भागों की तुलना करने पर-
\Rightarrow \frac{2 a^{3}-4 a}{4 a^{2}+1}=p, \frac{5 a^{2}-1}{4 a^{2}+1}=q
वर्ग करके जोड़ने पर –
p^{2}+q^{2}=\frac{\left(2 a^{3}-4 a\right)^{2}}{\left(4 a^{2}+1\right)^{2}}-\frac{\left(5 a^{2}-1\right)^{2}}{\left(4 a^{2}+1\right)^{2}}\\ \Rightarrow p^{2}+q^{2}=\frac{4 a^{6}-16 a^{4}+16 a^{2}+25 a^{4}-10 a^{2}+1}{\left(4 a^{2}+1\right)^{2}} \\ \Rightarrow p^{2}+q^{2} =\frac{4 a^{6}+9 a^{4}+6 a^{2}+1}{\left(4 a^{2}+1\right)^{2}} \\ \Rightarrow p^{2}+q^{2} =\frac{4 a^{6}+a^{4}+8 a^{4}+2 a^{2}+4 a^{2}+1}{\left(4 a^{2}+1\right)^{2}} \\ =\frac{a^{4} \left(4a^{2}+1\right)+2 a^{2}\left(4a^{2}+1\right)+1\left(4 a^{2}+1\right)}{\left(4 a^{2}+1\right)^{2}} \\ =\frac{\left(4 a^{2}+1\right)\left(a^{4}+2 a^{2}+1\right)}{\left(4 a^{2}+1\right)^{2}}\\ \Rightarrow p^{2}+q^{2}=\frac{\left(a^{4}+2 a^{2}+1\right)}{4 a^{2}+1}\\ \Rightarrow p^{2}+q^{2}=\frac{\left(a^{2}+1\right)^{2}}{4 a^{2}+1}
Example:8.यदि \left|z_{1}\right|=\left|z_{2}\right| तथा कोणांक z_{1} +कोणांक z_{2}=0 तो सिद्ध कीजिए कि z_{1}=\bar{z_{2}}
Solution:माना z_{1}=a+i b,z_{2}=c+i d \\ \left|z_{1}\right|=\left|z_{2}\right| \\ \Rightarrow |a+i b|=|c+i d| \\ \Rightarrow a^{2}+b^{2}=c^{2}+d^{2} \ldots(1)
कोणांक z_{1} +कोणांक z_{2}=0
\Rightarrow \tan^{-1} \left(\frac{b}{a}\right)+\tan^{-1} \left(\frac{d}{c}\right)=0 \\ \Rightarrow \tan^{-1} \left(\frac{b}{a}\right)=-\tan^{-1} \left(\frac{d}{c}\right) \\ \Rightarrow \tan^{-1} \left(\frac{b}{a}\right)=\tan^{-1} \left(-\frac{d}{c}\right) \\ \Rightarrow \frac{b}{a}=\frac{-d}{c} \\ \Rightarrow b=-\frac{a d}{c} \cdots(2)
समीकरण (1) व (2) से-
a^{2}+\frac{a^{2} d^{2}}{c^{2}}=c^{2}+d^{2} \\ \Rightarrow a^{2}\left(c^{2}+d^{2}\right)=c^{2}+d^{2} \\ \Rightarrow a^{2}=c^{2} \\ \Rightarrow a=c
समीकरण (2) में मान रखने पर-
b=-\frac{c d}{c} \\ \Rightarrow b=-d
अतः z_{1}=\bar{z}_{2}
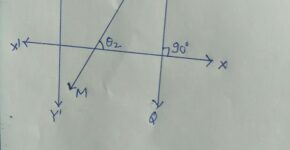
Example:9.यदि \theta_{1} ,\theta_{2} क्रमशः सम्मिश्र संख्याओं के कोणांक हैं तो सिद्ध कीजिए कि
z_{1} \bar{z}_{2}+\bar{z}_{1} z_{2}=2\left|z_{1}\right|\left|z_{2}\right| \cos \left(\theta_{1} -\theta_{2}\right)
Solution:माना z_{1}=a+i b \\ \bar{z}_{1} =a-i b \\ z_{2}=c+i d, \bar{z}_{2}=c-i d \\ \theta_{1}=\tan ^{-1}\left(\frac{b}{a}\right), \theta_{2}=\tan ^{-1}\left(\frac{d}{c}\right) \\ \theta_{1}-\theta_{2}=\tan ^{-1}\left(\frac{b}{a}\right)-\tan ^{-1}\left(\frac{d}{c}\right) \\ =\tan^{-1} \frac{\frac{b}{a}-\frac{d}{c}}{1+\left(\frac{b}{a}\right)\left(\frac{d}{c}\right)} \\ =\tan^{-1} \left(\frac{b c-a d}{a c+b d}\right) \\ \theta_{1}-\theta_{2}=\cos ^{-1} \frac{(a c+b d)}{\sqrt{\left(a^{2}+ b^{2}\right)\left(c^{2}+d^{2}\right)}} \\ \Rightarrow \cos \left(\theta_{1}-\theta_{2}\right)=\frac{a c+b d}{\sqrt{\left( a^{2}+b^{2} \right)\left(c^{2}+d^{2}\right)}} \\ z_{1} \bar{z}_{2}+\overline{z}_{1} z_{2}=2|z_{1}| |z_{2}| \cos \left(\theta_{1}-\theta_{2}\right)
L.H.S.= z_{1} \bar{z}_{2}+\bar{z}_{1} z_{2} \\ =(a+i b)(c-i d)+(a-i b)(c+i d)\\ z_{1} \bar{z}_{2}+\bar{z}_{1} z_{2}=2(ac+bd) \cdots(1)
R.H.S. 2|z_{1}| |z_{2}| \cos \left(\theta_{1}-\theta_{2}\right)\\ =2 \sqrt{a^{2}+b^{2}} \sqrt{c^{2}+d^{2}} \frac{a c+b d}{\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\\ 2|z_{1}|\left|z_{2}\right| \cos \left(\theta_{1}-\theta_{2} \right)=2(ac+b d) \cdots(2)
समीकरण (1) व (2) से-
z_{1} \bar{z}_{2}+\bar{z}_{1} z_{2}=2\left|z_{1}\right|\left|z_{2}\right| \cos \left(\theta_{1} -\theta_{2}\right)
Example:10.सिद्ध कीजिए कि \left(a+b \omega+c \omega^{2}\right)\left(a+b \omega^{2}+c \omega\right)=a^{3}+b^{3}+c^{3}-a b-b c-c a
Solution: \left(a+b \omega+c \omega^{2}\right)\left(a+b \omega^{2}+c \omega\right)=a^{3}+b^{3}+c^{3}-a b-b c-c a
L.H.S. \left(a+b \omega+c \omega^{2}\right)\left(a+b w^{2}+c \omega\right) \\ \Rightarrow a^{2}+a b \omega^{2}+a c \omega+a b \omega+b^{2} \omega^{3}+b c \omega^{2}+a c \omega^{2}+b c \omega^{4}+c^{2} \omega^{3} \\ \Rightarrow a^{2}+a b\left(\omega+\omega^{2}\right)+a c\left(\omega+\omega^{2}\right)+b^{2}(1)+b c \omega(1)+c^{2} a+b c \omega^{2}\left[\omega^{3}=1\right] \\ \Rightarrow a^{2}+a b(-1)+a c(-1)+b^{2}+b c\left(w+\omega^{2}\right)+c^{2}\left[\because 1+w+\omega^{2}=0\right] \\ \Rightarrow a^{2}+b^{2}+c^{2}-a b-b c-c a=R.H.S
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र संख्याओं (Complex Numbers) को समझ सकते हैं।
3.सम्मिश्र संख्याओं की समस्याएं (Complex Numbers Problems):
(1.)3-4i का वर्गमूल ज्ञात कीजिए।
(2.)यदि x=a+b, y=a w+b w^{2} तथा z=a \omega^{2}+b w तो सिद्ध कीजिए कि x^{2}+y^{2}+z^{2}=6 a b
(3.)सरल कीजिए: (x-1)^{3}+8=0
(4.)वह समीकरण ज्ञात कीजिए जिसके मूल समीकरण ax^{2}+bx+c=0 के मूलों के व्युत्क्रम हों।
उत्तर (Answers): (1)\sqrt{3-4i}=\pm (2-i) \\ (2)x=-1,1-2 \omega,1-2 \omega^{2} \\ (3)cx^{2}+bx+a=0
उपर्युक्त सवालों को हल करने पर सम्मिश्र संख्याओं (Complex Numbers) को समझ सकते हैं।
Also Read This Article:-Quadratic Equation
4.सम्मिश्र संख्याओं (Complex Numbers) के बारे में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.क्या 4 एक सम्मिश्र संख्या है? (Is 4 a complex number?):
उत्तर:पहली परिभाषा से,हम यह निष्कर्ष निकाल सकते हैं कि कोई भी काल्पनिक संख्या भी एक सम्मिश्र संख्या होती है।दूसरी परिभाषा से,हम यह निष्कर्ष निकाल सकते हैं कि कोई भी वास्तविक संख्या भी एक सम्मिश्र संख्या होती है।इसके अतिरिक्त,ऐसी सम्मिश्र संख्याएँ भी हो सकती हैं जो न तो वास्तविक हों और न ही काल्पनिक,जैसे 4 + 2 i ,4+2i 4+2i4,2, i।
प्रश्न:2.क्या 0 एक सम्मिश्र संख्या है? (Is 0 a complex number?):
उत्तर:हम कह सकते हैं कि शून्य एक सम्मिश्र संख्या है जिसका काल्पनिक भाग शून्य है,अर्थात् यह एक वास्तविक संख्या है।हम यह भी कह सकते हैं कि शून्य एक सम्मिश्र संख्या है जिसका वास्तविक भाग शून्य है अर्थात् यह एक काल्पनिक संख्या है।
प्रश्न:3.सम्मिश्र संख्याओं का प्रयोग किसके लिए किया जाता है? (What are complex numbers used for?):
उत्तर:सम्मिश्र संख्याओं का उपयोग
द्विघात के शून्यक (मूल) (Zeroes) ज्ञात करने के लिए सम्मिश्र संख्याओं का उपयोग किया जा सकता है।द्विघात सूत्र x के मानों के लिए ax^{2} + bx + c = 0 को हल करता है।यदि सूत्र वर्गमूल में ऋणात्मक मान प्रदान करता है,तो शून्य को सरल बनाने के लिए सम्मिश्र संख्याओं का उपयोग किया जा सकता है।इलेक्ट्रॉनिक्स और विद्युत चुंबकत्व में जटिल संख्याओं का उपयोग किया जाता है।
प्रश्न:4.सम्मिश्र संख्याओं का समुच्चय क्या है? (What is the set of complex numbers?):
उत्तर:सम्मिश्र संख्या वह संख्या है जिसे a+bi के रूप में लिखा जा सकता है,जहां a और b वास्तविक संख्याएं हैं और i परिभाषित काल्पनिक इकाई हैं जिसे i^2 = -1 द्वारा परिभाषित किया जाता है।सम्मिश्र संख्याओं के समुच्चय,जिसे C से निरूपित किया जाता है, में वास्तविक संख्याओं का समुच्चय (R) और शुद्ध काल्पनिक संख्याओं का समुच्चय शामिल है।
प्रश्न:5.सम्मिश्र संख्याओं में Z* क्या है? (What is Z* in complex numbers?):
उत्तर:सम्मिश्र संख्याएँ एक सम्मिश्र संख्या z को एक क्रमित युग्म z = (x, y) के रूप में परिभाषित किया जाता है, जहाँ x और y वास्तविक संख्याओं का एक युग्म है।
प्रश्न:6.क्या 5 एक सम्मिश्र संख्या है? (Is 5 a complex number?):
उत्तर:एक सम्मिश्र संख्या a + bi के रूप की एक संख्या है जहाँ i =काल्पनिक संख्या और a और b वास्तविक संख्याएँ हैं। उदाहरण के लिए, 5 + 3i, – + 4i,4.2-12i, और – +i सभी सम्मिश्र संख्याएँ हैं।a को सम्मिश्र संख्या का वास्तविक भाग कहा जाता है और b को सम्मिश्र संख्या का काल्पनिक भाग कहा जाता है।
प्रश्न:7.z* z संयुग्मी क्या है? (What is z * z conjugate?):
उत्तर:Z के सम्मिश्र संयुग्मी के लिए संकेतन या तो \bar{z} या z^{∗} है।सम्मिश्र संयुग्मी में वही वास्तविक भाग होता है जो z में होता है और वही काल्पनिक भाग होता है लेकिन विपरीत चिन्ह के साथ।अर्थात्,यदि z=a+ib, तो z^{∗}=a−ib.ध्रुवीय सम्मिश्र रूप में, re^{iθ} का सम्मिश्र संयुग्मी re^{-iθ} होता है।
प्रश्न:8.सम्मिश्र संख्याएँ धनात्मक हैं या ऋणात्मक? (Are complex numbers positive or negative?):
उत्तर:काल्पनिक संख्याएं, 0 और अनंत, जो गोलार्द्धों (Hemispheres) के बीच स्थित हैं, सभी “तटस्थ (Neutral)” हैं-अर्थात,न तो धनात्मक और न ही ऋणात्मक-लेकिन अन्य सभी सम्मिश्र संख्याएं या तो धनात्मक या ऋणात्मक हैं।
प्रश्न:9.आप सम्मिश्र संख्या की समस्याओं को कैसे हल करते हैं? (How do you solve complex number problems?):
उत्तर:कॉम्प्लेक्स नंबरों पर समस्याएं (1+i1)^{3} को A + iB के रूप में व्यक्त करें जहां A और B वास्तविक संख्याएं हैं।
सम्मिश्र राशि (2 – 3i)(-1 + 7i) का मापांक ज्ञात कीजिए।
-4 का मुख्य कोणांक (Principle Amplitude) और मापांक (Modulus) ज्ञात कीजिए।
सम्मिश्र संख्या -2 + 2√3i का कोणांक (Amplitude) और मापांक ज्ञात कीजिए।
प्रश्न:10.आप एक सम्मिश्र संख्या का कैसे पता करते हैं? (How do you find a complex number?):
उत्तर:एक सम्मिश्र संख्या एक वास्तविक संख्या और एक काल्पनिक संख्या का योग है।एक सम्मिश्र संख्या मानक रूप में व्यक्त की जाती है जब a+bi लिखा जाता है जहाँ a वास्तविक भाग होता है और bi काल्पनिक भाग होता है।उदाहरण के लिए, 5+2i एक सम्मिश्र संख्या है।तो 3+4√3i भी है।
प्रश्न:11.5 एक सम्मिश्र संख्या क्यों है? (Why is 5 a complex number?):
उत्तर:इसमें काल्पनिक भाग 0 है।यह अंक विशुद्ध रूप से वास्तविक है।उदाहरण 17 के वास्तविक और काल्पनिक भागों को बताएं।वास्तव में सभी वास्तविक संख्याओं को सम्मिश्र संख्या माना जा सकता है,जिनमें शून्य काल्पनिक भाग होता है।
प्रश्न:12.आप एक सम्मिश्र संयुग्मी कैसे ज्ञात करते हैं? (How do you find a complex conjugate?):
उत्तर:आप सम्मिश्र संयुग्मी को सम्मिश्र संख्या के काल्पनिक भाग के चिन्ह को बदलने से ही पाते हैं। 4+7i का सम्मिश्र संयुग्म ज्ञात करने के लिए हम काल्पनिक भाग के चिन्ह को बदलते हैं।इस प्रकार 4+7i का सम्मिश्र संयुग्मी 4 – 7i है।
प्रश्न:13.1/Z का मापांक क्या है? (What is the modulus of 1/Z?):
उत्तर:z व्युत्क्रम का मापांक और कोणांक
z के व्युत्क्रम का मापांक \frac{1}{|z|} के बराबर है। |\frac{1}{z}|=\frac{1}{|z|}
z के व्युत्क्रम का कोणांक z के संयुग्मी संख्या के कोणांक के बराबर है। arg(\frac{1}{z})= -arg(z).
प्रश्न:14.आप दो सम्मिश्र संख्याओं को कैसे जोड़ते हैं? (How do you add two complex numbers?):
उत्तर:दो सम्मिश्र संख्याओं को जोड़ने या घटाने के लिए, बस संबंधित वास्तविक और काल्पनिक भागों को जोड़ें या घटाएं।उदाहरण के लिए,5 + 3i और 4 + 2i का योग 9 + 5i है।दूसरे के लिए,3 + i और -1 + 2i का योग 2 + 3i है।
प्रश्न:15.सम्मिश्र संख्या का ऋणात्मक क्या है? (What is the negative of the complex number?):
उत्तर:हालाँकि,एक सम्मिश्र संख्या के ऋणात्मक को इस प्रकार परिभाषित किया गया है: मान लीजिए z=a+ib एक सम्मिश्र संख्या है।फिर z के ऋणात्मक को इस प्रकार परिभाषित किया जाता है: -z=-a-ib.
प्रश्न:16.कौन सा सम्मिश्र संख्या का रूप नहीं है? (Which is not a form of complex number?):
उत्तर:(Nitrogen does not form complexes because of the absence of d-orbitals)
डी-ऑर्बिटल्स की अनुपस्थिति के कारण नाइट्रोजन कॉम्प्लेक्स नहीं बनाता है।
प्रश्न:17.सम्मिश्र संख्या का जनक कौन है ? (Who is the father of complex number?):
उत्तर:कैस्पर वेसल (Caspar Wessel)
उत्तर:सम्मिश्र तल (उपरोक्त) में एक बिंदु के रूप में एक सम्मिश्र संख्या का विचार पहली बार 1799 में डेनिश-नार्वेजियन (Danish-Norwegian) गणितज्ञ कैस्पर वेसल (Caspar Wessel) द्वारा वर्णित किया गया था,हालांकि वालिस (Wallis) के ए ट्रीटीज़ एलजेब्रा (A Treatise Algebra) में 1685 की शुरुआत में इसका अनुमान लगाया गया था।
प्रश्न:18.क्या सम्मिश्र संख्याएँ मौजूद हैं? (Do complex numbers exist?):
उत्तर:हालांकि यह एक वास्तविक संख्या नहीं है तब इसे संख्या रेखा पर निर्धारित नहीं किया जा सकता है लेकिन काल्पनिक संख्याएं इस अर्थ में “वास्तविक (Real)” हैं तो वे मौजूद (Exist) हैं और गणित में उपयोग की जाती हैं।काल्पनिक संख्याएँ, जिन्हें सम्मिश्र संख्याएँ भी कहा जाता है,का उपयोग वास्तविक जीवन के अनुप्रयोगों में किया जाता है, जैसे कि बिजली के साथ ही द्विघात समीकरण में।
प्रश्न:19.आप एक सम्मिश्र संख्या को कैसे विभाजित करते हैं? (How do you divide a complex number?):
उत्तर:सम्मिश्र संख्याओं को विभाजित करने के लिए,आपको संयुग्मी से गुणा करना होगा।किसी सम्मिश्र संख्या का संयुग्मी ज्ञात करने के लिए आपको बस इतना करना है कि हर में दो पदों के बीच के चिह्न को बदल दें।चरण 2: कोष्ठक को हटाने के लिए अंश और हर दोनों में (or FOIL) वितरित करें (Distribute (or FOIL) in both the numerator and denominator to remove the parenthesis)।
प्रश्न:20.सम्मिश्र संख्याएँ कैसे अस्तित्व में आईं? (How did complex numbers come into existence?):
उत्तर:1831 में, कार्ल फ्रेडरिक गॉस (Carl Friedrich Gauss ) ने Argand के विचार को लोकप्रिय बनाया और इसे कई लोगों के सामने पेश किया।इसके अलावा, गॉस ने डेसकार्टेस का a+bi संकेतन लिया और इसे एक सम्मिश्र संख्या कहा। सम्मिश्र संख्याओं को स्वीकार करने के लिए, अधिकांश भाग के लिए,दुनिया को प्राप्त करने के लिए इन सभी लोगों को एक साथ काम करना पड़ा।
प्रश्न:21.आप सम्मिश्र मूल कैसे ज्ञात करते हैं? (How do you find complex roots?):
उत्तर:काल्पनिक या सम्मिश्र मूल तब उत्पन्न होंगे जब द्विघात सूत्र के मूल भाग (Radical Portion) अर्थात् करणी चिन्ह के अंतर्गत मान ऋणात्मक होगा।ध्यान दें कि मूल भाग (Radical Portion) के अन्तर्गत मान “b^{2} - 4ac” द्वारा दर्शाया गया है।इसलिए, यदि b^{2} - 4ac एक ऋणात्मक मान है,तो द्विघात समीकरण में सम्मिश्र संयुग्मी मूल होंगे (containing “i “) होगा।
प्रश्न:22.आप वास्तविक और सम्मिश्र मूल कैसे ज्ञात करते हैं? (How do you find real and complex roots?):
उत्तर:वास्तविक संख्याओं का कोई काल्पनिक भाग नहीं होता है और शुद्ध काल्पनिक संख्याओं का कोई वास्तविक भाग नहीं होता है।उदाहरण के लिए यदि x = 7 बहुपद का एक मूल है,तो इस मूल को वास्तविक और सम्मिश्र दोनों माना जाता है क्योंकि इसे x = 7 + 0i (काल्पनिक भाग 0 है) के रूप में फिर से लिखा जा सकता है।
प्रश्न:23.क्या प्रत्येक बहुपद का एक सम्मिश्र शून्य होता है? (Does every polynomial have a complex zero?):
उत्तर:बीजगणित के मौलिक प्रमेय (fundamental theorem of algebra) में कहा गया है कि सम्मिश्र गुणांक वाले प्रत्येक गैर-अचर एकल-चर बहुपद (every non-constant single-variable polynomial with complex coefficients) में कम से कम एक सम्मिश्र मूल होता है।इसमें वास्तविक गुणांक वाले बहुपद शामिल हैं,क्योंकि प्रत्येक वास्तविक संख्या एक सम्मिश्र संख्या होती है जिसका काल्पनिक भाग शून्य के बराबर होता है।
प्रश्न:24.सम्मिश्र संख्याओं का प्रयोग सर्वप्रथम किसने किया? (Who first utilized complex numbers?):
उत्तर:गिरोलामो कार्डानो (Girolamo Cardano)
जटिल संख्याओं की आवश्यकता को महसूस करने वाले पहले गणितज्ञों में से एक इतालवी गणितज्ञ गिरोलामो कार्डानो (1501-1576) थे।1545 के आसपास, कार्डानो ने माना कि घन समीकरणों को हल करने के उनके तरीके से अक्सर ऋणात्मक संख्याओं के वर्गमूल वाले समाधान निकलते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र संख्याएं (Complex Numbers),सम्मिश्र संख्याओं का कोणांक (Complex Numbers Argument) को समझ सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र संख्याएं (Complex Numbers),सम्मिश्र संख्याओं का कोणांक (Complex Numbers Argument) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |