Tangents and Normals
1.स्पर्श रेखाएं और अभिलम्ब (Tangents and Normals)-
स्पर्श रेखाएं और अभिलम्ब में स्पर्शरेखा(Tangents and Normals) वह सरल रेखा है जो किसी दिए गए बिंदु पर वक्र को स्पर्श करती है। अभिलम्ब ऐसी सरल रेखा है जो स्पर्शरेखा के लंबवत है।
यहां हम अवकलन के प्रयोग से किसु दिए गए वक्र के किसी बिन्दु पर स्पर्शरेखा तथा अभिलम्ब के समीकरण ज्ञात करेंगे।
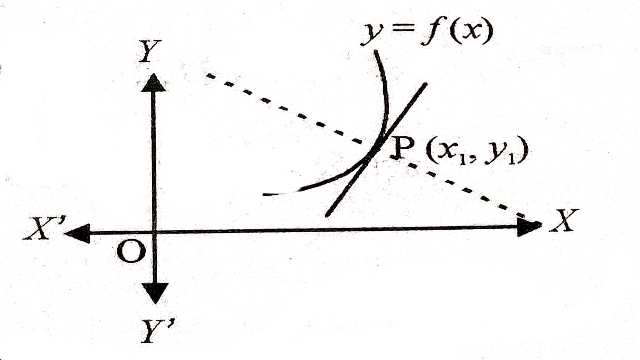
वक्र y=f(x) के किसी बिन्दु \left(x_{1}, y_{1}\right) पर स्पर्शरेखा की प्रवणता या ढाल \left(\frac{d y}{d x}\right)_{(x_{1}, y_{1})} होती है।अतः वक्र के बिन्दु \left(x_{1}, y_{1}\right) पर स्पर्शरेखा का समीकरण निम्न होगा-
y-y_{1}=\left(\frac{d y}{d x}\right)_{(x_{1}, y_{1})}\left(x-x_{1}\right)
चूंकि वक्र के किसी बिन्दु पर अभिलम्ब,उस बिन्दु पर स्पर्शरेखा के लम्बवत् होता है, अतः वक्र के स्पर्श बिन्दु \left(x_{1}, y_{1}\right) पर अभिलम्ब की प्रवणता -\frac{1}{\left(\frac{d y}{d x}\right)_{(x_{1}, y_{1})}} है।
अतः वक्र y=f(x) के बिन्दु पर अभिलम्ब के समीकरण निम्न हैं-
y-y_{1}=-\frac{1}{\left(\frac{d y}{d x}\right)_{(x_{1}, y_{1})}}\left(x-x_{1}\right) \\ \Rightarrow\left(y-y_{1}\right) \left(\frac{d y}{d x}\right)_{(x_{1} y_{1})} +\left(x-x_{1}\right)=0
टिप्पणी:यदि वक्र y=f(x) की कोई स्पर्शरेखा x-अक्ष की धन दिशा से \psi कोण बनाए तब \frac{d y}{d x}=स्पर्शरेखा की प्रवणता=\tan \psi
विशेष स्थितियां
(i)यदि \psi=0 अर्थात् स्पर्शरेखा x-अक्ष के समान्तर हो तब \frac{d y}{d x}=\tan 0=0 होगा।इस स्थिति में बिन्दु पर स्पर्शरेखा x-अक्ष के समान्तर होती है।
(ii)यदि \psi=90^{\circ} अर्थात् स्पर्शरेखा x-अक्ष के लम्बवत् हो तब \frac{d y}{d x}=\tan 0=\infty होगा।इस स्थिति में बिन्दु \left(x_{1}, y_{1}\right) पर स्पर्शरेखा x-अक्ष के लम्बवत् होती है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Differentiation
2.स्पर्श रेखाएं और अभिलम्ब के उदाहरण (Tangents and Normals Examples),स्पर्शरेखा और अभिलम्ब की समस्याएं हल सहित (Tangent and Normal Lines Problems with Solutions)-
Example-1.वक्र y =x^{3}-x बिन्दु x=2 पर स्पर्शरेखा की प्रवणता ज्ञात कीजिए।
Solution–y =x^{3}-x \\ (\frac{d y}{d x})=3 x^{2}-1 \\ \left(\frac{d y}{d x}\right)_{(x=2)}=3(2)^{2}-1 \\ =12-1 \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(x=2)}=11
Example-2.वक्र y=\frac{x-1}{x-2}, x \neq 2 के बिन्दु x=10 पर स्पर्शरेखा की प्रवणता ज्ञात कीजिए।
Solution–y=\frac{x-1}{x-2} \\\Rightarrow\left(\frac{d y}{d x}\right)=\frac{(x-2)(1)-(x-1)(1)}{(x-2)^{2}} \\ \Rightarrow \frac{d y}{d x}=\frac{x-2-x+1}{(x-2)^{2}} \\ \Rightarrow \frac{d y}{d x}=\frac{-1}{(x-2)^{2}} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(x=10)}=-\frac{1}{(10-2)^{2}} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(x=10)}=-\frac{1}{64}
Example-3.वह बिन्दु ज्ञात कीजिए जहां वक्र y=\sqrt{(4 x-3)} की स्पर्शरेखा की प्रवणता \frac{2}{3} है।
Solution–y =\sqrt{(4 x-3)} \cdots(1) \\ \frac{d y}{d x} =\frac{1}{2 \sqrt{(4 x-3)}} \cdots (4) \\\Rightarrow\left(\frac{d y}{x}\right) =\frac{2}{\sqrt{(4 x-3)}} \\ \left(\frac{d y}{d x}\right) =\frac{2}{3} (दिया है)
अतः \frac{2}{3} =\frac{2}{\sqrt{(4 x-3)}} \\ \Rightarrow \sqrt{(4 x-3)}=3 \\ \Rightarrow 4 x-3=9 \\ \Rightarrow 4 x=12 \\ \Rightarrow x=3
x का मान समीकरण (1) में रखने पर-
y=\sqrt{4 \times 3-3} \\ \Rightarrow y=\sqrt{12-3} \\ \Rightarrow y=\sqrt{9} \\ \Rightarrow y=\pm 3
अतः उस बिन्दु के निर्देशांक हैं (3,3);(3,-3)
Example-4.उन सभी रेखाओं के समीकरण ज्ञात कीजिए जो वक्र y+\frac{2}{x-3}=0 की स्पर्शरेखाएं हैं तथा जिनकी प्रवणता 2 है।
Solution–y+\frac{2}{x-3}=0 \\ \Rightarrow y=-\frac{2}{x-3} \\ \frac{d y}{d x}=\frac{2}{(x-3)^{2}} \\ \frac{d y}{d x}=2 (दिया है)
2=\frac{2}{(x-3)^{2}}\\ \Rightarrow(x-3)^{2}=1 \Rightarrow x-3=\pm 1\\ \Rightarrow x-3=1 \Rightarrow x=4\\ x-3=-1 \Rightarrow x=2
यदि x=4 तो y=-\frac{2}{x-3} \\ \Rightarrow y=-\frac{2}{4-3} \\ \Rightarrow y=-2
यदि x=2 तो y=-\frac{2}{2-3} \\ \Rightarrow y=2
अतः बिन्दु (4,-2) तथा (2,2) व प्रवणता वाली स्पर्शरेखाओं के समीकरण-
y-y_{1}=\frac{d y}{d x}\left(x-x_{1}\right) \\ \Rightarrow y+2=2(x-4) \Rightarrow 2 x-y=10 \\ y-2=2(x-2) \Rightarrow 2 x-y=2
Example-5.वक्र \frac{x^{2}}{4}+\frac{y^{2}}{25} =1 पर वे बिन्दु ज्ञात कीजिए जहां स्पर्शरेखा
(i)x-अक्ष के समान्तर (ii)y-अक्ष के समान्तर
Solution–\frac{x^{2}}{4}+\frac{y^{2}}{25} =1....(1) \\ \frac{2 x}{4}+\frac{2 y}{25} \frac{d y}{d x}=0 \\ \Rightarrow \frac{d y}{d x}=-\frac{2 x}{4} \times \frac{25}{2 y} \\ \Rightarrow \frac{d y}{d x}=-\frac{25 x}{4 y}
(i)x-अक्ष के समान्तर \frac{d y}{d x}=0 \\ \frac{-25 x}{4 y}=0 \\ \Rightarrow x=0
समीकरण (1) में रखने पर-
\frac{y^{2}}{25}=1 \\ \Rightarrow y^{2}=25 \\ \Rightarrow y=\pm 5
अतः बिन्दु के निर्देशांक (0,5);(0,-5)
(ii)y-अक्ष के समान्तर \frac{d y}{d x}=\infty \\ \Rightarrow -\frac{25 x}{4 y}=\infty \\ -\frac{25 x}{4 y}=\frac{1}{0} \Rightarrow 4 y=0 \\ \Rightarrow y=0
समीकरण (1) में रखने पर-
\frac{x^{2}}{4}=0 \\ \Rightarrow x^{2}=4 \\ \Rightarrow x=\pm 2
अतः यदि स्पर्शरेखा y-अक्ष के समान्तर है तो बिन्दु के निर्देशांक (2,0);(-2,0)
Example-6.वक्र x=a \sin ^{3} t, y=b \cos ^{3} t की t= \frac{\pi}{2} पर स्पर्शरेखा का समीकरण ज्ञात कीजिए।
Solution–x=a \sin ^{3} t, y=b \cos ^{3} t \\ \frac{d x}{d t}=3 a \sin ^{2} t \cos t, \quad \frac{d y}{d t}=-3 b \cos ^{2} t \sin t \\ \frac{d y}{d x} =\frac{d y}{d t} \cdot \frac{d t}{d x} \\ =-\frac{3 b \cos ^{2}+\sin t}{3 a \sin ^{2}+\cos t} \\ \Rightarrow \frac{d y}{d x} =\frac{-b \cos t}{a \sin t} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(\frac{\pi}{2})}=-\frac{b \cos \frac{\pi}{2}}{a \sin \frac{\pi}{2}} \\ \Rightarrow \left(\frac{d y}{d x}\right)_{(\frac{\pi}{2})}=0 \\ x=a \sin ^{3} t \\ \Rightarrow x=a \sin ^{3} \frac{\pi}{2} \Rightarrow x=a \\ \Rightarrow y=b \cos ^{3} t \Rightarrow y=b \cos ^{3} \frac{\pi}{2} \\ \Rightarrow y=0
अतः (a,0) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\left(\frac{dy}{d x}\right)\left(x-x_{1}\right) \\ \Rightarrow y-0=0(x-a) \\ \Rightarrow y=0
Example-7.वक्र y=\sin ^{2} x के बिन्दु (\frac{\pi}{3}, \frac{3}{4}) पर अभिलम्ब का समीकरण ज्ञात कीजिए।
Solution–y=\sin ^{2} x \\ \frac{d y}{d x}=2 \sin x \cos x \\ \left(\frac{d y}{d x}\right)_{(\frac{\pi}{3}, \frac{3}{4})} =2 \sin \frac{\pi}{3} \cos \frac{\pi}{3} \\ =2 \times \frac{\sqrt{3}}{2} \times \frac{1}{2} \\ \Rightarrow\left(\frac{d y}{d x}\right) _{(\frac{\pi}{3}, \frac{3}{4})}=\frac{\sqrt{3}}{2}
अतः बिन्दु (\frac{\pi}{3}, \frac{3}{4}) पर अभिलम्ब की समीकरण-
(y-y_{1})\left(\frac {d y} {d x}\right)+\left(x-x_{1}\right)=0 \\ \Rightarrow \left(y-\frac{3}{4}\right)\left(\frac{\sqrt{3}}{2}\right)+(x-\frac{\pi}{3})=0 \\ \Rightarrow \frac{(4 y-3) \sqrt{3}}{8}+\frac{3 x-\pi}{3}=0 \\ \Rightarrow (12 y-9) \sqrt{3}+24 x-8 \pi=0 \\ \Rightarrow 24 x+12 \sqrt{3} y=9 \sqrt{3}+8 \pi
निम्नलिखित वक्रों के लिए उनके सम्मुख अंकित बिन्दु पर स्पर्शरेखा एवम् अभिलम्ब के समीकरण ज्ञात कीजिए
Example-8. y=x^{2}+4 x+1, x=3 पर
Solution–y=x^{2}+4 x+1 \quad....(1) \\ \frac{d y}{d x}=2 x+4 \\ \Rightarrow \left(\frac{d y}{d x}\right)_{(x=3)}=2(3)+4 \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(x=3)}=10
x=3 समीकरण (1) में रखने पर-
y=x^{2}+4 x+1 \\ \Rightarrow y=3^{2}+4(3)+1 \\ \Rightarrow y=9+12+1 \\ \Rightarrow y=22
अतः बिन्दु (3,22) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\left(\frac{d y}{d x}\right)\left(x-x_{1}\right) \\ \Rightarrow y-22=10(x-3) \\ \Rightarrow 40 x-y=8
बिन्दु (3,22) पर अभिलम्ब का समीकरण-
\left(y-y_{1}\right)\left(\frac{d y}{d x}\right)+\left(x-x_{1}\right)=0 \\ \Rightarrow(y-22)(10)+(x-3)=0 \\ \Rightarrow 10 y-220+x-3=0 \\ \Rightarrow x+10 y=223
स्पर्शरेखा 10x-y=8
अभिलम्ब x+10y=223
Example-9.y^{2}=4 a x,x=a पर
Solution:-y^{2}=4a x \cdots (1)
x=a रखने पर-
y^{2}=4a(a) \\ y^{2}=4 a^{2} \\ y=\pm 2 a
अतः बिन्दु (a,2a),(a,-2a)
समीकरण (1) का x के सापेक्ष अवकलन करने पर-
2 y\left(\frac{d y}{dx}\right)=4 a \\ \Rightarrow \frac{d y}{d x}=\frac{2 a}{y} \\ \left(\frac{d y}{d x}\right)_{\left(a, 2a\right)}=\frac{2 a}{2 a} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(a, 2a)}=1 \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(a, 2a)}=\frac{2 a}{-2a} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(a,-4 a)}=-1
अतः (a,2a) तथा (a,-2a) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\left(\frac{d y}{dx}\right)\left(x-x_{1}\right) \\ \Rightarrow y-2a=1(x-a) \\ \Rightarrow y-2 a=x-a \\ \Rightarrow x-y+a=0 \\ y +2 a=-1(x-a) \\ \Rightarrow x+2a=-x+a \\ \Rightarrow x+y+a=0
बिन्दु (a,2a) तथा (a,-2a) पर अभिलम्ब का समीकरण-
\left(y-y_{1}\right)\left(\frac{d y}{d x}\right)+\left(x-x_{1}\right)=0 \\ \Rightarrow (y-2 a)(1)+(x-2 a)=0 \\ \Rightarrow x+y-3 a=0 \\ (y+2 a)(-1)+(x-a)=0 \\ \Rightarrow x-y-3 a=0
अतः स्पर्शरेखा x+y+a=0,x-y+a=0
अभिलम्ब x-y-3a=0, x+y-3a=0
Example-10.x y=a^{2},\left(a t, \frac{a}{t}\right) पर
Solution–x y=a^{2} \\ x \frac{ d y}{d x}+y=0 \\ \Rightarrow\left(\frac{d y}{d x}\right)=-\frac{y}{x} \\ \Rightarrow \left( \frac{d y}{d x}\right)_{(a t, \frac{a}{t})}=\frac{-y}{x} \\ =\frac{-\frac{a}{t}}{a t} \\ \Rightarrow\left(\frac{d y}{x}\right)_{(a t, \frac{a}{t})}=-\frac{1}{t^{2}}
अतः बिन्दु (a t, \frac{a}{t}) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\frac{d y}{dx}(x-x_{1}) \\ \Rightarrow y-\frac{a}{t}=\left(\frac{-1}{t^{2}}\right)(x-a t) \\ \Rightarrow y t^{2}-a t=-x+a t \\ \Rightarrow x+y t^{2}-2 a t=0
बिन्दु (a t, \frac{a}{t}) पर अभिलम्ब का समीकरण-
(y-y_{1})\left(\frac{d y}{d x}\right)+\left(x-x_{1}\right)=0 \\ \Rightarrow \left(y-\frac{a}{t}\right)\left(-\frac{1}{t^{2}}\right)+(x-a t)=0 \\ \Rightarrow \frac{(yt-a)}{t}\left(-\frac{1}{t^{2}}\right) +(x-a t)=0 \\ \Rightarrow x t^{3}-y t+a-a t^{4}=0 \\ \Rightarrow x t^{3}-y t=a t^{4}-a
स्पर्शरेखा x+y t^{2}-2 a t=0
अभिलम्ब x t^{3}-y t=a t^{4}-a
Example-11. y^{2}=4a x,\left(\frac{a}{m^{2}}, \frac{2 a}{m}\right) पर
Solution–y^{2}=4 a x \\ 2 y \frac{d y}{d x}=4 a \\ \Rightarrow\left(\frac{d y}{d x}\right)=\frac{2 a}{y} \\ \Rightarrow \left(\frac{d y}{d x}\right)_{(\frac{a}{m^{2}}, \frac{2 a}{m})}=\frac{2a}{\left(\frac{2 a}{m}\right)} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(\frac{a}{m^{2}}, \frac{2 a}{m})}=m
अतः बिन्दु (\frac{a}{m^{2}}, \frac{2 a}{m}) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\left(\frac{d y}{d x}\right)\left(x-x_{1}\right) \\ \Rightarrow y-\frac{2 a}{m}=m\left(x-\frac{a}{m^{2}}\right) \\ \Rightarrow m y-2 a=m^{2}\left(x-\frac{a}{m^{2}}\right) \\ \Rightarrow m y-2 a=m^{2} x-a \\ \Rightarrow y-m x=\frac{a}{m}
बिन्दु पर अभिलम्ब का समीकरण-
\left(y-y_{1}\right)\left(\frac{d y}{d x}\right)+\left(x-x_{1}\right)=0 \\ \Rightarrow\left(y-\frac{2 a}{m}\right)(m)+\left(x-\frac{a}{m^{2}}\right)=0 \\ \Rightarrow m y-2 a+x-\frac{a}{m^{2}}=0 \\ \Rightarrow x+m y=2 a+\frac{a}{m^{2}}
अतः स्पर्शरेखा y-m x=\frac{a}{m}
अभिलम्ब x+m y=2 a+\frac{a}{m^{2}}
Example-12. \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1,(a \sec \theta, b \tan \theta) पर
Solution–\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \\ \frac{2 x}{a^{2}}-\frac{2 y}{b^{2}} \frac{d y}{d x}=0 \\ \Rightarrow \frac{d y}{d x}=\frac{2 x}{a^{2}} \times \frac{b^{2}}{2 y} \\ \Rightarrow \frac{d y}{d x}=\frac{b^{2} x}{a^{2} y} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(a \sec \theta, b \tan \theta)}=\frac{b^{2} \cdot a \sec \theta}{a^{2} \cdot b \tan \theta} \\ \Rightarrow\left(\frac{d y}{d x}\right)_{(a \sec \theta, b \tan \theta)}=\frac{b}{a \sin \theta}
अतः बिन्दु (a \sec \theta, b \tan \theta) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\frac{d y}{d x}\left(x-x_{1}\right) \\ \Rightarrow y-b \tan \theta=\left(\frac{b}{a \sin \theta}\right)(x-a \sec \theta) \\ \Rightarrow \frac{y}{b}-\tan \theta=\frac{x}{a \sin \theta}-\frac{\sec \theta}{\sin \theta} \\ \Rightarrow \frac{x}{a \sin \theta}-\frac{y}{b}=\frac{\sec \theta}{\sin \theta}-\tan \theta \\ \Rightarrow \frac{x}{a \sin \theta}-\frac{y}{b}=\frac{1}{\sin \theta \cos \theta}-\frac{\sin \theta}{\cos \theta} \\ \Rightarrow \frac{x}{a \sin \theta}-\frac{y}{b}=\frac{1}{\cos \theta}\left(\frac{1}{\sin \theta}-\sin \theta\right) \\ \Rightarrow \frac{x}{a \sin \theta}-\frac{y}{b}=\frac{1}{\cos \theta \sin \theta}\left(1-\sin ^{2} \theta\right) \\ \Rightarrow \frac{x}{a \sin \theta}- \frac{y}{b}=\frac{\cos ^{2} \theta}{\cos \theta \sin \theta} \\ \Rightarrow \frac{x}{a \sin \theta} -\frac{y}{b}=\cot \theta \\ \Rightarrow \frac{x}{a} \sec \theta-\frac{y}{b} \tan \theta=1
बिन्दु (a \sec \theta, b \tan \theta) पर अभिलम्ब का समीकरण-
y-y_{1}(\frac{d y}{dx})+\left(x-x_{1}\right)=0 \\ \Rightarrow (y-b \tan \theta)\left(\frac{b}{a \sin \theta}\right)+(x-a \sec \theta)=0\\ \Rightarrow \frac{b^{2} y}{\sin \theta}-\frac{b^{2}}{\cos \theta}+a x-a^{2} \sec \theta=0 \\ \Rightarrow \frac{b y}{\sin \theta}+a x=\frac{b^{2}}{\cos \theta}+a^{2} \sec \theta \\ \Rightarrow a x+\frac{b y}{\sin \theta} =\frac{a^{2} +b^{2}}{\cos \theta} \\ \Rightarrow a x \cos \theta+b y \cot \theta=a^{2}+b^{2}
Example-13.y=2 x^{2}-3 x-1,(1,-2) पर
Solution–y=2 x^{2}-3 x-1 \\ \frac{d y}{d x}=4 x-3 \\ \left(\frac{d y}{d x}\right)_{(1,-2)}=4(1)-3=1
अतः (1,-2) पर स्पर्शरेखा का समीकरण-
y-y_{1}=\frac{d y}{d x}\left(x-x_{1}\right) \\ y+2=1(x-1) \\ \Rightarrow x-y=3
बिन्दु (1,-2) पर अभिलम्ब का समीकरण-
\left(y-y_{1}\right)\left(\frac{d y}{d x}\right)+\left(x-x_{1}\right)=0 \\ \Rightarrow(y+2)(1)+(x-1)=0 \\ \Rightarrow x+y+1=0
उपर्युक्त उदाहरणों के द्वारा स्पर्श रेखाएं और अभिलम्ब (Tangents and Normals) को समझ सकते हैं।
3.स्पर्श रेखाएं और अभिलम्ब की समस्याएं (Tangents and Normals Problems),स्पर्शरेखा और अभिलम्ब के सवाल (Tangents and Normals Questions)-
निम्नलिखित वक्रों के लिए उनके सम्मुख अंकित बिन्दु पर स्पर्शरेखा एवम् अभिलम्ब के समीकरण ज्ञात कीजिए।
(1.) x=a t^{2}, y=2 a t,t=1
(2.) x=\theta+\sin \theta, y=1-\cos \theta, \theta=\frac{\pi}{2} पर
(3.)वक्र x^{\frac{2}{3}}+y^{\frac{2}{3}}=2 के बिन्दु (1,1) पर स्पर्शरेखा तथा अभिलम्ब के समीकरण ज्ञात कीजिए।
(4.)वक्र y=x^{3}-11x+5 पर उस बिन्दु को ज्ञात कीजिए जिस पर स्पर्शरेखा y=x-11 है।
(5.)वक्र 2x^{2}-y^{2}=14 पर सरल रेखा x+3y=6 के समान्तर अभिलम्ब के समीकरण ज्ञात कीजिए।
(6.) सिद्ध कीजिए कि x के प्रत्येक मान के लिए सरल रेखा \frac{x}{a}+\frac{y}{b}=2 वक्र \left(\frac{x}{a}\right)^{n}+\left(\frac{y}{b}\right)^{n}=1 को बिन्दु (a,b) पर स्पर्श करती है।
उत्तर (Andwers):
(1.)स्पर्शरेखा x-y+a=0 अभिलम्ब x+y-3a=0
(2.)स्पर्शरेखा 2x-2y-\pi=0 , अभिलम्ब 2x-2y-\pi-4=0
(3.)स्पर्शरेखा x+y-2=0, अभिलम्ब y-x=0
(4.)(-2,9)
(5.)x+3y=9, x+3y+9=0
उपर्युक्त सवालों को हल करके स्पर्श रेखाएं और अभिलम्ब (Tangents and Normals) को ठीक से समझ सकते हैं।
Also Read This Article:-Differentiability
स्पर्श रेखाएं और अभिलम्ब (Tangents and Normals) में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न1-आप अभिलम्ब और स्पर्शरेखा कैसे ज्ञात करते हैं? (How do you find normals and tangents?)-
स्पर्शरेखा एक सरल रेखा है जो किसी दिए गए बिंदु पर वक्र को स्पर्श करती है। अभिलम्ब भी एक सरल रेखा है जो स्पर्शरेखा के लंबवत है।हम इस तथ्य का भी उपयोग करते हैं कि अगर ग्रेडिएंट्स m_{1} और m_{2} के साथ क्रमशः दो लाइनें लम्बवत् हैं, तो m_{1}m_{2} = -1
स्पर्शरेखा तथा अभिलम्ब एक दूसरे के लम्बवत् होती है।
यदि आप किसी वक्र के समीकरण का अवकलन करते हैं, तो आपको वक्र के ढाल के लिए एक सूत्र मिलेगा।
प्रश्न2-स्पर्शरेखा और अभिलम्ब का समीकरण क्या है? (What is equation of tangent and normal?)-
y-y_{1}=\frac{d y}{d x}\left(x-x_{1}\right)
वक्र के समीकरण का अवकलन करके बिन्दु (x_{1},y_{1}) पर स्पर्शरेखा की प्रवणता ज्ञात की जाती है।
स्पर्शरेखा तथा अभिलम्ब की प्रवणता में निम्न सम्बन्ध होता है- m_{1}m_{2}=-1
इस सूत्र से अभिलम्ब की प्रवणता ज्ञात कर अभिलम्ब की समीकरण ज्ञात की जा सकती है।
प्रश्न3-स्पर्शरेखा के समीकरण का सूत्र क्या है? (What is the formula for equation of tangent?)-
y-y_{1}=\frac{d y}{d x}\left(x-x_{1}\right)
प्रश्न4-स्पर्शरेखा की परिभाषा क्या है? (What is definition of tangent?)
प्रश्न5-स्पर्शरेखा और अभिलम्ब सूत्र (Tangents and Normals Formulas)
स्पर्शरेखा \rightarrow y-y_{1}=\frac{d y}{d x}\left(x-x_{1}\right)
अभिलम्ब \rightarrow \left(y-y_{1}\right) \left(\frac{d y}{d x}\right)_{(x_{1} y_{1})} +\left(x-x_{1}\right)=0
प्रश्न6-डेरिवेटिव स्पर्शरेखा और अभिलम्ब के अनुप्रयोग (Application of Derivatives Tangents and Normals)
उपर्युक्त प्रश्नों के उत्तर द्वारा स्पर्श रेखाएं और अभिलम्ब (Tangents and Normals) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |