Middle term of binomial expansion
1.”द्विपद प्रसार में मध्य पद” का परिचय (Introduction to”Middle term of binomial expansion,Middle term in binomial expansion”)-
द्विपद प्रसार में मध्य पद (Middle term of binomial expansion,middle term in binomial expansion) ज्ञात करने के लिए पदों की संख्या सम होगी तो दो मध्य पद होंगे तथा यदि पदों की संख्या विषम होगी तो एक मध्य पद होगा।
द्विपद प्रसार में कई शब्दों का प्रयोग किया जाता है, सबसे पहले उनका अर्थ जानते हैं-
(1.)द्विपद व्यंजक (Binomial Expression)-
कोई दो पद वाला व्यंजक,द्विपद व्यंजक अथवा द्विपद कहलाता है। दोनों पद परस्पर धन अथवा ऋण चिन्ह द्वारा जुड़े होते हैं। जैसे x+a में x प्रथम पद तथा a द्वितीय पद है।
(2.)द्विपद प्रमेय (Binomial Theorem)-
जिस सूत्र के द्वारा किसी द्विपद व्यंजक के किसी भी घात का विस्तार (Expansion) एक श्रेणी के रूप में किया जाता है, उस सूत्र को द्विपद प्रमेय कहते हैं।
(3.)द्विपद गुणांक (Binomial Coefficient)-द्विपद व्यंजक{ (x+a) }^{ n } के विस्तार में x की विभिन्न घातों के गुणांक द्विपद गुणांक कहलाते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Examples of complex numbers
2.द्विपद प्रसार में व्यापक पद (General term in binomial expansion)-
प्रसार में (r+1) वें पद को व्यापक पद कहते हैं।इसे { T }_{ r+1 } से व्यक्त किया जाता है।अर्थात्
{ T }_{ r+1 }=^{ n }{ { C }_{ r } }{ x }^{ n-r }{ a }^{ r }
इसमें r=0,1,2,3,………रखकर प्रसार के प्रथम,द्वितीय,तृतीय,चतुर्थ पद,……..ज्ञात किए जा सकते हैं जिन्हें क्रमशः { T }_{ 1 },{ T }_{ 2 },{ T }_{ 3 },{ T }_{ 4 }....से व्यक्त करते हैं।
इस प्रकार { T }_{ 1 }=^{ n }{ { C }_{ 0 } }{ x }^{ n }\\ { T }_{ 2 }=^{ n }{ { C }_{ 1 } }{ x }^{ n-1 }{ a }^{ 1 }\\ { T }_{ 3 }=^{ n }{ { C }_{ 2 } }{ x }^{ n-2 }{ a }^{ 2 }\\ { T }_{ 4 }=^{ n }{ { C }_{ 3 } }{ x }^{ n-3 }{ a }^{ 3 }
3.धन पूर्णांक घातांक के लिए द्विपद प्रसार से सम्बन्धित महत्त्वपूर्ण जानकारियां-
एक द्विपद विस्तार में कितने पद हैं? (How many terms are in a binomial expansion?),द्विपद विस्तार में पदों की संख्या (Number of terms in binomial expansion)-
(1.){ (x+a) }^{ n } के प्रसार में पदों की संख्या,घात से एक अधिक अर्थात् (n+1) होती है।
(2.)प्रसार में x की घात क्रमशः घटती जाती है और a की घात क्रमशः बढ़ती जाती है।प्रत्येक पद में x और a की घातांकों का योग द्विपद के घातांक (n) के बराबर होता है।
(3.)प्रसार के प्रारम्भ और अंत से समान दूरी वाले पदों के गुणांक बराबर होते हैं।
^{ n }{ { C }_{ 0 } }=^{ n }{ { C }_{ n } }=1,na=^{ n }{ { C }_{ n-1 } },^{ n }{ { C }_{ 2 } }=^{ n }{ { C }_{ n-2 } }.....
^{ n }{ { C }_{ r } }=^{ n }{ { C }_{ n-r } },(1\le r\le n)
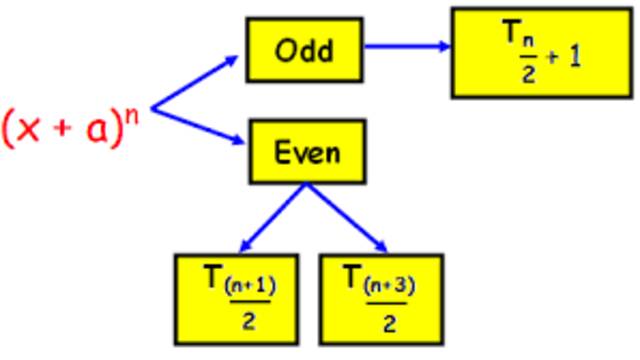
4.द्विपद प्रसार में मध्य पद (Middle term of binomial expansion,Middle term in binomial expansion,Middle term of binomial expansion formula,what is the middle term of a binomial expansion)-
(1.)यदि घात सम है,तो प्रसार में पदों की संख्या विषम होगी, इसलिए मध्य पद एक ही होगा।
मध्य पद=(\frac { n }{ 2 } +1)=(\frac { n+2 }{ 2 } )=[\frac { (n+1)+1 }{ 2 } ]
= \frac { प्रसार\quad में\quad पदों\quad की\quad संख्या+1 }{ 2 } वां पद
(2.) यदि घात n विषम है,तो प्रसार में पदों की संख्या सम होगी, इसलिए मध्य पद दो होंगे।
मध्य पद=(\frac { n+1 }{ 2 } ) वां पद तथा (\frac { n+1 }{ 2 } +1)=(\frac { n+3 }{ 2 } ) वां पद
5.द्विपद प्रसार में मध्य पद (Middle term of binomial expansion,Middle term in binomial expansion) पर आधारित सवाल-
निम्नलिखित प्रसार में मध्य पद ज्ञात कीजिए (Find middle term of binomial expansion),How to find middle term of binomial expansion?-
Question-1.{ (\frac { x }{ 2 } +2y) }^{ 6 }
Solution-{ (\frac { x }{ 2 } +2y) }^{ 6 } के प्रसार में पदों की संख्या=6+1=7(विषम)
अतः मध्य पद=(\frac { n+2 }{ 2 } )वां पद
=(\frac { 6+2 }{ 2 } ) वां पद
= 4 चौथा पद
{ T }_{ r+1 }=^{ n }{ { C }_{ r } }{ x }^{ n-r }{ a }^{ r }
r=3,n=6,a=2y
{ T }_{ 4 }=^{ 6 }{ { C }_{ 3 } }{ (\frac { x }{ 2 } ) }^{ 6-3 }{ (2y) }^{ 3 }\\ \Rightarrow { T }_{ 4 }=\frac { 6! }{ 3!3! } { (\frac { x }{ 2 } ) }^{ 3 }{ (2y) }^{ 3 }\\ \Rightarrow { T }_{ 4 }=\frac { 6\times 5\times 4\times 3\times 2\times 1 }{ 3\times 2\times 1\times 3\times 2\times 1 } \frac { { x }^{ 3 } }{ 8 } .8{ y }^{ 3 }\\ \Rightarrow { T }_{ 4 }=20{ x }^{ 3 }{ y }^{ 3 }
Question-2.{ (3a-\frac { { a }^{ 3 } }{ 6 } ) }^{ 9 }
Solution-– { (3a-\frac { { a }^{ 3 } }{ 6 } ) }^{ 9 } के प्रसार में पदों की संख्या=9+1=10(सम है) अतः मध्य पद=(\frac { n+1 }{ 2 } ) वां पद तथा (\frac { n+3 }{ 2 } ) वां पद
=(\frac { 9+1 }{ 2 } ) वां पद तथा(\frac { 9+3 }{ 2 } ) वां पद
=5वां पद तथा 6वां पद
{ T }_{ r+1 }=^{ n }{ { C }_{ r } }{ x }^{ n-r }{ a }^{ r }
r=4,n=9,x=3a,a=-\frac { { a }^{ 3 } }{ 6 } \\ { T }_{ 5 }=^{ 9 }{ { C }_{ 4 } }{ (3a) }^{ 9-4 }{ (-\frac { { a }^{ 3 } }{ 6 } ) }^{ 4 }\\ =\frac { 9! }{ 5!4! } { (3a) }^{ 5 }\frac { { a }^{ 12 } }{ { 6 }^{ 4 } } \\ =\frac { 9\times 8\times 7\times 6\times 5! }{ 5!\times 4\times 3\times 2\times 1 } { 3 }^{ 5 }{ a }^{ 5 }.\frac { { a }^{ 12 } }{ { 6 }^{ 4 } } \\ =9\times 2\times 7\times \frac { { 3 }^{ 5 }{ a }^{ 17 } }{ { (3\times 2) }^{ 4 } } \\ =\frac { { 3 }^{ 5 }\times 7{ a }^{ 17 } }{ { 2 }^{ 3 } } \\ =\frac { 189{ a }^{ 17 } }{ 8 }
r=5,n=9,x=3a,a=-\frac { { a }^{ 3 } }{ 6 } \\ { T }_{ 6 }=^{ 9 }{ { C }_{ 5 } }{ (3a) }^{ 9-5 }{ (-\frac { { a }^{ 3 } }{ 6 } ) }^{ 5 }\\ =\frac { 9! }{ 5!4! } { (3a) }^{ 4 }(-\frac { { a }^{ 15 } }{ { 6 }^{ 5 } } )\\ =-\frac { 9\times 8\times 7\times 6\times 5! }{ 5!\times 4\times 3\times 2\times 1\times 5! } { 3 }^{ 4 }{ a }^{ 4 }.\frac { { a }^{ 15 } }{ { (3\times 2) }^{ 5 } } \\ =-9\times 2\times 7\times \frac { { 3 }^{ 4 }{ a }^{ 19 } }{ { 3 }^{ 5 }\times { 2 }^{ 5 } } \\ =-\frac { { 3 }\times 7{ a }^{ 19 } }{ { 2 }^{ 4 } } \\ =-\frac { 21{ a }^{ 19 } }{ 16 }
Question-3.{ (x+\frac { 1 }{ x } ) }^{ 2n }
Solution-{ (x+\frac { 1 }{ x } ) }^{ 2n }के प्रसार में पदों की संख्या=(2n+1)वां पद (विषम)
अतः मध्य पद=(\frac { n+2 }{ 2 } )वां पद
= (\frac { 2n+2 }{ 2 } )वां पद
= (n+1) वां पद
r=n,x=x,a=\frac { 1 }{ x } \\ { T }_{ r+1 }=^{ n }{ { C }_{ r } }{ x }^{ n-r }{ a }^{ r }\\ { T }_{ n+1 }=^{ 2n }{ { C }_{ n } }{ (x) }^{ 2n-n }{ (\frac { 1 }{ x } ) }^{ n }\\ =\frac { 2n! }{ n!n! } { (x) }^{ n }\frac { 1 }{ { x }^{ n } } \\ \Rightarrow { T }_{ n+1 }=\frac { 2n! }{ n!n! } \\ \Rightarrow { T }_{ n+1 }=\frac { 2n! }{ { (n!) }^{ 2 } }
Question-4.{ (3x-\frac { 2 }{ { x }^{ 2 } } ) }^{ 15 }
Solution-{ (3x-\frac { 2 }{ { x }^{ 2 } } ) }^{ 15 }के प्रसार में पदों की संख्या=15+1=16(सम) अतः मध्य पद= (\frac { n+1 }{ 2 } ) वां पद तथा(\frac { n+3 }{ 2 } ) वां पद
=(\frac { 15+1 }{ 2 } ) वां पद तथा (\frac { 15+3 }{ 2 } )वां पद
=8वां पद तथा 9वां पद
n=15,r=7,x=3x,a=-\frac { 2 }{ { x }^{ 2 } } \\ { T }_{ r+1 }=^{ n }{ { C }_{ r } }{ x }^{ n-r }{ a }^{ r }\\ { T }_{ 8 }=^{ 15 }{ { C }_{ 7 } }{ (3x) }^{ 15-7 }{ (-\frac { 2 }{ { x }^{ 2 } } ) }^{ 7 }\\ \Rightarrow { T }_{ 4 }=-\frac { 15! }{ 8!7! } { (3x) }^{ 8 }\frac { { 2 }^{ 7 } }{ { x }^{ 14 } } \\ \Rightarrow { T }_{ 4 }=-\frac { 15\times 14\times 13\times 12\times 11\times 10\times 9\times 8! }{ 8!\times 7\times 6\times 5\times 4\times 3\times 2\times 1 } .{ 3 }^{ 8 }{ x }^{ 8 }\times \frac { { 2 }^{ 7 } }{ { x }^{ 14 } } \\ \Rightarrow { T }_{ 4 }=-\frac { 6435\times { 3 }^{ 8 }\times { 2 }^{ 7 } }{ { x }^{ 6 } }
n=15,r=8,x=3x,a=-\frac { 2 }{ { x }^{ 2 } } \\ { T }_{ 9 }=^{ 15 }{ { C }_{ 8 } }{ (3x) }^{ 15-8 }{ (-\frac { 2 }{ { x }^{ 2 } } ) }^{ 8 }\\ \Rightarrow { T }_{ 4 }=\frac { 15! }{ 8!7! } { (3x) }^{ 7 }\frac { { 2 }^{ 88 } }{ { x }^{ 16 } } \\ \Rightarrow { T }_{ 4 }=\frac { 15\times 14\times 13\times 12\times 11\times 10\times 9\times 8! }{ 8!\times 7\times 6\times 5\times 4\times 3\times 2\times 1 } .{ 3 }^{ 7 }{ x }^{ 7 }\times \frac { { 2 }^{ 8 } }{ { x }^{ 16 } } \\ \Rightarrow { T }_{ 4 }=\frac { 6435\times { 3 }^{ 7 }\times { 2 }^{ 8 } }{ { x }^{ 9 } }
Question-5.{ (\frac { x }{ 2 } -\frac { y }{ 3 } ) }^{ 6 }
Solution–{ (\frac { x }{ 2 } -\frac { y }{ 3 } ) }^{ 6 } के प्रसार में पदों की संख्या=(6+1)=7(विषम)
अतः मध्य पद=(\frac { n+2 }{ 2 } ) वां पद
=(\frac { 6+2 }{ 2 } ) वां पद
= 4 (चौथा पद)
r=3,n=6,x=\frac { x }{ 2 } ,a=-\frac { y }{ 3 } \\ { T }_{ r+1 }=^{ n }{ { C }_{ r } }{ x }^{ n-r }{ a }^{ r }\\ { T }_{ 4 }=^{ 6 }{ { C }_{ 3 } }{ (\frac { x }{ 2 } ) }^{ 6-3 }{ (-\frac { y }{ 3 } ) }^{ 3 }\\ \Rightarrow { T }_{ 4 }=-\frac { 6! }{ 3!3! } \frac { { x }^{ 3 } }{ { 2 }^{ 3 } } \frac { y^{ 3 } }{ { 3 }^{ 3 } } \\ \Rightarrow { T }_{ 4 }=-\frac { 6\times 5\times 4\times 3! }{ 3!\times 3\times 2\times 1 } \frac { { x }^{ 3 }y^{ 3 } }{ { 2 }^{ 3 }{ 3 }^{ 3 } } \\ \Rightarrow { T }_{ 4 }=-\frac { 20{ x }^{ 3 }y^{ 3 } }{ { 2 }^{ 3 }{ 3 }^{ 3 } } \\ \Rightarrow { T }_{ 4 }=-\frac { 5{ x }^{ 3 }y^{ 3 } }{ 54 }
इस प्रकार उपर्युक्त सवालों के हल के द्वारा द्विपद प्रसार में मध्य पद (Middle term of binomial expansion,Middle term in binomial expansion) को समझा जा सकता है।
6.द्विपद विस्तार में मध्यम पद का गुणांक (Coefficient of middle term in binomial expansion,Define middle term of a binomial expansion)-
मध्य पद n के मूल्य पर निर्भर करता है।
(1) जब n सम है तो { (x+y) }^{ n } के विस्तार में पदों की संख्या n+1 ,सम हैं। अतः एक मध्य पद होगा।(\frac { n+2 }{ 2 } ) मध्य पद होगा।
(2) जब n विषम है, तो { (x+y) }^{ n } के विस्तार में कुल पदों की संख्या n + 1 (सम) है।तो, दो मध्य पद हैं यानि (\frac { n+1 }{ 2 } ) वें और (\frac { n+3 }{ 2 } ) वें दो मध्य पद हैं।जब विस्तार में दो मध्य पद होते हैं तो उनके द्विपद गुणांक बराबर होते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा द्विपद प्रसार में मध्य पद (Middle term of binomial expansion,middle term in binomial expansion) को समझा जा सकता है।
Also Read This Article:-Sum of first n term of an AP
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |