Straight Line Class 11
1.सरल रेखा कक्षा 11 (Straight Line Class 11),गणित में सरल रेखा (Straight Line In Mathematics):
सरल रेखा कक्षा 11 (Straight Line Class 11) बिन्दुओं का समुच्चय है,अतः दो बिन्दुओं के बीच दूरी को रेखा या सरल रेखा कहते हैं।
रेखा की ढाल (Slope of a Line):
निर्देशांक तल में एक रेखा x-अक्ष के साथ दो कोण बनाती है जो परस्पर सम्पूरक होते हैं।कोण \theta (मान लीजिए) जो रेखा l,x-अक्ष की धनात्मक दिशा के साथ बनाती है,रेखा l का झुकाव (inclination of the line l) कहलाता है।स्पष्टतया 0^{\circ} \leq \theta<180^{\circ} (आकृति)
हम देखते हैं कि x-अक्ष पर संपाती रेखाओं का झुकाव 0° होता है।एक ऊर्ध्व रेखा (y-अक्ष के समान्तर या y-अक्ष पर संपाती) का झुकाव 90° है।
परिभाषाःयदि \theta किसी रेखा l का झुकाव है तो \tan \theta को रेखा l की ढाल कहते हैं।
वह रेखा जिसका झुकाव 90° है,उसकी ढाल परिभाषित नहीं है।एक रेखा की ढाल को m से व्यक्त करते हैं।इस प्रकार m=\tan \theta, \theta \neq 90^{\circ} यह देखा जा सकता है कि x-अक्ष की ढाल शून्य है और y अक्ष की ढाल परिभाषित नहीं है।
रेखा की ढाल जब उस पर दो बिन्दु दिए गए हों (Slope of a line when coordinates of any two points on the line are given):
हम जानते हैं कि यदि एक रेखा पर दो बिन्दु ज्ञात हों तो वह पूर्णतया परिभाषित होती है।अतः हम रेखा की ढाल को उस पर दिए गए दो बिन्दुओं के निर्देशांकों के पद में ज्ञात करते हैं।
मान लीजिए कि एक ऊर्ध्वेत्तर (non-vertical) रेखा l, जिसका झुकाव \theta है,पर दो बिन्दु P\left(x_{1}, y_{1}\right) और Q\left(x_2, y_2\right) हैं।स्पष्टतया x_{1} \neq x_{2} अन्यथा रेखा x-अक्ष पर लम्ब होगी,जिसकी ढाल परिभाषित नहीं है।रेखा l का झुकाव \theta, न्यूनकोण या अधिक कोण हो सकता है।हम दोनों स्थितियों पर विचार करते हैं।
x-अक्ष पर QR तथा RQ पर लम्ब PM खींचिए (आकृति (i) और (ii) में दर्शाया गया है)।
दशा 1. जब \theta न्यूनकोण आकृति (i) में \angle MPQ=\theta इसलिए रेखा l की ढाल m=\tan \theta \cdots(1)
परन्तु त्रिभुज \triangle MPQ में \tan \theta=\frac{M Q}{M P}=\frac{y_2-y_1}{x_2-x_1} \cdots(2)
समीकरण (1) तथा (2) से हम पाते हैं कि
m=\frac{y_2-y_1}{x_2-x_1}
दशा II जब \theta अधिक कोणः
आकृति (ii) में \angle MPQ=180^{\circ}-\theta
इसलिए \theta=180^{\circ}-\angle MPQ
अब रेखा l की ढाल =m=\tan \theta \\ =\tan \left(180^{\circ}-\angle M P Q\right) \\ =-\tan \angle MPQ \\ =-\frac{M Q}{M P}=-\frac{\left(y_2-y_1\right)}{\left(x_1-x_2\right)} \\ =\frac{y_2-y_1}{x_2-x_1}
फलतः दोनों दशाओं में बिन्दु \left(x_1, y_1\right) और \left(x_2, y_2\right) से जाने वाली रेखा की ढाल
m=\frac{y_2-y_1}{x_2-x_1}
दो रेखाओं के समान्तर और परस्पर लम्ब होने का प्रतिबन्ध (Conditions for parallelism and perpendicularity of lines):
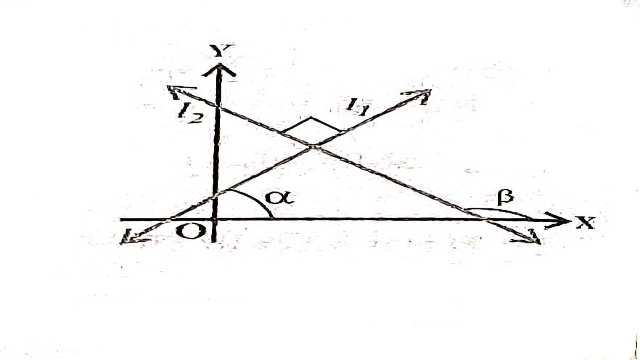
मान लीजिए कि उर्ध्वाधर रेखाओं l_{1} और l_{2} की ढालें,जो एक निर्देशांक तल में हैं क्रमशः m_{1} और m_{2} हैं।यदि l_{1} और l_{2} समान्तर रेखाएँ हैं (आकृति) तब उनके झुकाव समान होंगे।
अर्थात् \alpha=\beta और \tan \alpha=\tan \beta
इसलिए m_{1}=m_{2} अर्थात् उनके ढाल बराबर हैं।
विलोमतः यदि दो रेखाओं l_{1} और l_{2} के ढाल बराबर हैं
अर्थात् m_1=m_2
तब \tan \alpha=\tan \beta
स्पर्शज्या (Tangent) फलन के गुणधर्म से (0° और 180° के बीच)
\alpha=\beta अतः रेखाएँ समान्तर हैं।
अतः दो ऊर्ध्वेत्तर रेखाएँ l_{1} और l_{2} समान्तर होती हैं यदि और केवल यदि उनके ढाल समान हैं।
यदि रेखाएँ l_{1} और l_{2} परस्पर लम्ब हैं (आकृति) तब \beta=\alpha+ 90^{\circ} \\ =-\cot \alpha=-\frac{1}{\tan \alpha}
अर्थात् m_2=-\frac{1}{m_1} या m_{1} m_{2}=-1
विलोमतः यदि m_{1} m_{2}=-1 अर्थात् \tan \alpha \tan \beta=-1
तब \tan \alpha=-\cot \beta=\tan \left(\beta+90^{\circ}\right) या \tan \left(\beta-90^{\circ}\right)
इसलिए \alpha और \beta का अन्तर 90° है।
अतः रेखाएँ \alpha और \beta परस्पर लम्ब हैं।
इसलिए l_{1} और l_{2} परस्पर लम्ब हैं ।
अतः दो ऊर्ध्वेत्तर रेखाएँ l_{1} और l_{2} परस्पर लम्ब होती हैं यदि और केवल यदि उनकी ढाल परस्पर ऋणात्मक व्युत्क्रम है।
अर्थात् m_2=-\frac{1}{m_1} या m_1 m_2=-1
दो रेखाओं के बीच कोण (Angle between two lines):
जब हम एक तल में स्थित एक से अधिक रेखाओं के बारे में विचार करते हैं तब देखते हैं कि या तो ये रेखाएँ प्रतिच्छेद करती हैं या समान्तर होती हैं।यहाँ हम दो रेखाओं के बीच के कोण पर, उनके ढालों के पदों पर विचार करते हैं।
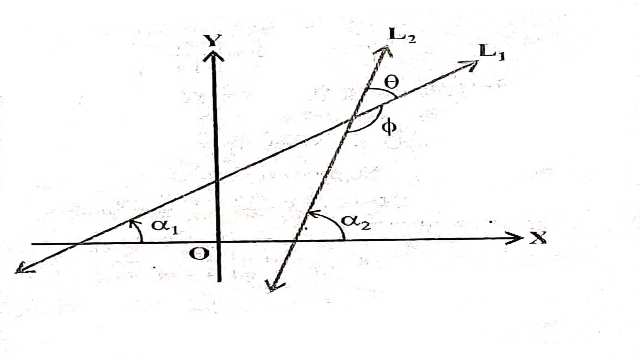
मान लीजिए दो ऊर्ध्वेत्तर रेखाओं L_{1} और L_{2} के ढाल क्रमशः m_1 और m_2 है।यदि और के झुकाव क्रमशः \alpha_1 और \alpha_2 हों तो
m_1=\tan \alpha_1 और m_2=\tan \alpha_2
हम जानते हैं कि जब दो रेखाएँ परस्पर प्रतिच्छेद करती हैं तब वे दो शीर्षाभिमुख कोणों के युग्म बनाती हैं जो ऐसे हैं कि किन्हीं दो संलग्न कोणों का योग 180° है।मान लीजिए कि रेखाओं L_{1} और L_{2} के बीच संलग्न कोण \theta और\phi हैं तब
\theta=\alpha_2-\alpha_1 और \alpha_1, \alpha_2 \neq 90^{\circ}
इसलिए \tan \theta=\tan \left(\alpha_2-\alpha_1\right)=\frac{\tan \alpha_{2}-\tan \alpha_{1}}{1+\tan \alpha_1 \tan \alpha_2} \\ \Rightarrow \tan \theta=-\frac{\left(m_1-m_2\right)}{1+m_1 m_2} (क्योंकि 1+m_1 m_2 \neq 0)
और \phi=180^{\circ}-\theta
इस प्रकार \tan \phi=\tan \left(180^{\circ}-\theta\right)\\ =-\tan \theta \\ \tan \phi= \frac{m_2-m_1}{1+m_1 m_2}( क्योंकि 1+m_1 m_2 \neq 0)
अब दो स्थितियाँ उत्पन्न होती हैंः
स्थिति I.यदि \frac{m_2-m_1}{1+m_1 m_2} धनात्मक है तब \tan \theta धनात्मक होगा और \tan \phi ऋणात्मक होगा जिसका अर्थ है \theta न्यूनकोण होगा और \phi अधिक कोण होगा।
स्थिति II.यदि \frac{m_2-m_1}{1+m_1 m_2} ऋणात्मक है तब \tan \theta ऋणात्मक होगा और \tan \phi धनात्मक होगा जिसका अर्थ है \theta अधिक कोण होगा और \phi न्यून कोण होगा।
इस प्रकार m_1 और m_2 ढाल वाली रेखाओं L_1 और L_2 के बीच का न्यून कोण (माना कि \theta) इस प्रकार है,
\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| (जहाँ 1+m_1 m_2 \neq 0)
अधिक कोण (माना कि \phi) \phi=180-\theta के प्रयोग से प्राप्त किया जा सकता है।
तीन बिन्दुओं की संरेखता (Collinearity of three points):
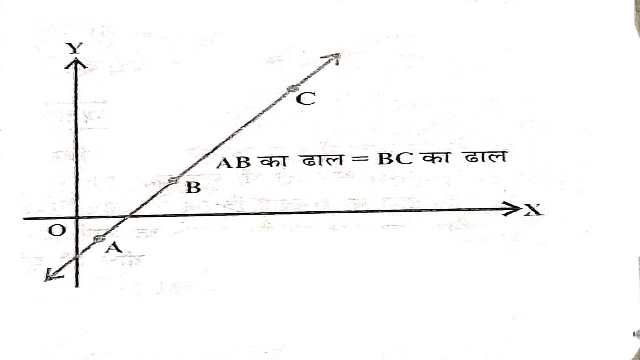
हम जानते हैं कि दो समान्तर रेखाओं के ढाल समान होते हैं।यदि समान ढाल वाली दो रेखाएँ एक ही बिन्दु से होकर जाती हैं तो आवश्यक रूप से वे संपाती (Coincident) होती हैं।अतः यदि XY-तल में A,B और C तीन बिन्दु हैं तब वे एक रेखा पर होंगे अर्थात् तीनों बिन्दु संरेख होंगे (आकृति) यदि और केवल यदि AB की ढाल=BC की ढाल
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Geometric and Arithmetic Progression
2.सरल रेखा कक्षा 11 के साधित उदाहरण (Straight Line Class 11 Solved Examples):
Example:1.कार्तीय तल में एक चतुर्भुज खींचिए जिसके शीर्ष (-4,5),(0,7),(5,-5) और (-4,-2) हैं।इसका क्षेत्रफल ज्ञात कीजिए।
Solution:माना A(-4,-2),B(5,-5),C(0,7),D(-4,5)
त्रिभुज का क्षेत्रफल=\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2 \right)\right]
\triangle ABC का क्षेत्रफल=\frac{1}{2}[-4(-5-7)+5(7-(-2))+0(-2-(-5))] \\ =\frac{1}{2}[-4 \times-12+5(7+2)+0] \\ =\frac{1}{2}[48+45] \\ =\frac{1}{2} \times 93 \\ =\frac{93}{2}
\triangle ACD का क्षेत्रफल=\frac{1}{2}[-4(7-5)+0(5-(-2))-4(-2-7)] \\ =\frac{1}{2}[-4 \times 2-4 \times-9] \\ =\frac{1}{2}[-8+36] \\ =+\frac{28}{2}
अतः चतुर्भुज ABCD का क्षेत्रफल=\frac{93}{2}+\frac{28}{2} =\frac{121}{2} वर्ग इकाई
Example:2.2a भुजा के समबाहु त्रिभुज का आधार y-अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिन्दु मूल बिन्दु है।त्रिभुज के शीर्ष ज्ञात कीजिए।
Solution: \text{लम्ब}=\sqrt{\text{कर्ण}^{2}-\text{आधार}^{2}} \\ =\sqrt{(2 a)^2-(a)^2} \\=\sqrt{4 a^2-a^2} \\=\pm \sqrt{3}a
अतः त्रिभुज के शीर्ष (\sqrt{3}a,0),(0,-a) या (-\sqrt{3}a,0),(0,-a)
Example:3. P\left(x_1, y_1\right) और Q\left(x_2, y_2\right) के बीच की दूरी ज्ञात कीजिए जबः(i) PQ, y-अक्ष के समान्तर है, (ii)PQ, x-अक्ष के समान्तर है।
Solution:(i) P\left(x_1, y_1\right), Q\left(x_2, y_2\right)
y-अक्ष के समान्तर x_1=x_2 \\ \text{PQ}=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\ =\sqrt{\left( x_1-x_1\right)^2+\left(y_2-y_1\right)^2} \\ \Rightarrow P Q=\sqrt{\left(y_2-y_1\right)^2} \\ \Rightarrow P Q=\left|y_2-y_1\right|
(ii)x-अक्ष के समान्तर
y_1=y_2 \\ \text{PQ}=\sqrt{\left(x_2-x_1\right)^2+\left(y_1-y_1\right)^2} \\ =\sqrt{\left(x_2-x_1\right)^2} \\ \Rightarrow P Q=\left|x_2-x_1\right|
Example:4.x-अक्ष पर एक बिन्दु ज्ञात कीजिए जो (7,6) और (3,4) बिन्दुओं से समान दूरी पर है।
Solution:x-अक्ष पर y=0
अतः x-अक्ष पर बिन्दु के निर्देशांक A(x,0)
B(7,6),C(3,4)
\Rightarrow A B=A C \\ \Rightarrow A B^2=A C^2 \\ \Rightarrow \left(\sqrt{(x-7)^2+(0-6)^2}\right)^2= \left(\sqrt{(x-3)^2+(0-4)^2}\right)^2 \\ \Rightarrow (x-7)^2+(-6)^2=(x-3)^2+(-4)^2 \\ \Rightarrow x^2-14 x+49+36=x^2-6 x+9+16 \\ \Rightarrow -14 x+6 x=25-85 \\ \Rightarrow -8 x=-60 \\ \Rightarrow x=\frac{60}{8}=\frac{15}{2}
अतः बिन्दु के निर्देशांक हैंः \left( \frac{15}{2},0 \right )
Example:5.रेखा की ढाल ज्ञात कीजिए जो मूल बिन्दु और P(0,-4) तथा B(8,0) बिन्दुओं को मिलाने वाले रेखाखण्ड के मध्य बिन्दु से जाती है।
Solution:मध्य बिन्दुः \left(\frac{x_2+x_1}{2}, \frac{y_2+y_1}{2}\right)
P(0,-4) तथा B(8,0) का मध्य बिन्दु
=\left(\frac{0+8}{2}, \frac{-4+0}{2}\right) \\ =(4,-2)
(0,0) तथा (4,-2) से गुजरने वाली रेखा की ढाल =\frac{y_2-y_1}{x_2-x_1} \\ =-\frac{2-0}{4-0} \\ =-\frac{2}{4} \\ m=-\frac{1}{2}
Example:6.पाइथागोरस प्रमेय के प्रयोग बिना दिखलाइए कि बिन्दु (4,4),(3,5) और (-1,-1) एक समकोण त्रिभुज के शीर्ष हैं।
Solution:\tan \theta =\frac{y_2-y_1}{x_2-x_1} \\ = \frac{5-4}{3-4} \\ = \frac{1}{-1} \\ =-1 \\ \Rightarrow \tan \theta =-\tan 45 \\ \Rightarrow \tan \theta=\tan (180-45) \\ \Rightarrow \theta=135^{\circ}
अतः समकोण त्रिभुज के शीर्ष नहीं है क्योंकि समकोण त्रिभुज का कोई भी कोण अधिक कोण नहीं होता।
Example:7.उस रेखा का समीकरण ज्ञात कीजिए जो y-अक्ष की धन दिशा से वामावर्त मापा गया 30° का कोण बनाती है।
Solution:m=\tan (90+30) \\ \Rightarrow m=-\cot 30 \\ \Rightarrow m=-\sqrt{3}
रेखा का समीकरण y=m x+c \\ y=-\sqrt{3} x+c
Example:8.x का वह मान ज्ञात कीजिए जिसके लिए बिन्दु (x,-1),(2,1) और (4,5) संरेख हैं।
Solution:A(x,-1),B(2,1),C(4,5)
संरेख होने का प्रतिबन्ध
AB का ढाल=BC का ढाल
\frac{1-(-1)}{2-x}=\frac{5-1}{4-2} \\ \Rightarrow \frac{1+1}{2-x}=\frac{4}{2} \\ \Rightarrow 4=4(2-x) \\ \Rightarrow 1=2-x \\ \Rightarrow x=2-1 \\ \Rightarrow x=1
Example:9.दूरी सूत्र का प्रयोग किए बिना दिखलाइए कि बिन्दु (-2,-1),(4,0),(3,3) और (-3,2) एक समान्तर चतुर्भुज के शीर्ष है।
Solution:A(-2,-1),B(4,0),C(3,3),D(-3,2)
AB का ढाल m_1=\frac{y_2-y_1}{x_2-x_1} \\ =\frac{0-(-1)}{4-(-2)} \\ =\frac{1}{4+2} \\ m_1=\frac{1}{6}
BC का ढाल m_2=\frac{3-0}{3-4} \\ \Rightarrow m_{2}=-3
AB व BC के बीच कोण
\tan \theta=\frac{m_2-m_1}{1+m_1 m_2} \\ =\frac{-3-\frac{1}{6}}{1+\left(\frac{1}{6}\right)(-3)} \\ =\frac{-\frac{18-1}{6}}{\frac{6-3}{6}} \\ \Rightarrow \tan \theta =\frac{-19}{+3} \\ \Rightarrow \theta =\tan ^{-1} \left(\frac{-19}{3}\right)
CD की ढाल=\frac{2-3}{-3-3}=\frac{1}{6}
BC व CD के बीच कोण
\tan \phi=\frac{\frac{1}{6}-(-3)}{1+\frac{-1}{6} (-3)} \\=\frac{\frac{1}{6}+3}{\frac{6-3}{6}} \\ =\frac{ \frac{19}{6}}{\frac{3}{6}} \\ =\frac{19}{3} \\ \phi=\tan ^{-1}\left(\frac{19}{3}\right) \\ \theta+\phi=\tan ^{-1}\left(-\frac{19}{3}\right)+\tan ^{-1}\left(\frac{19}{3}\right) \\ =\tan ^{-1}\left(\frac{-\frac{19}{3}+ \frac{19}{3}}{1+\left(-\frac{19}{3}\right) \left(\frac{19}{3}\right)}\right) \\ =\tan ^{-1} 0 \\ \theta+ \phi=180^{\circ}
आसन्न कोणों का योग 180° है अतः ABCD समान्तर चतुर्भुज है।
Example:10.x-अक्ष और (3,-1) और (4,-2) बिन्दुओं को मिलाने वाली रेखा के बीच कोण ज्ञात कीजिए।
Solution:x-अक्ष की ढाल m_{2}=\frac{-2-(-1)}{4-3} \\ =\frac{-2+1}{1} \\ \Rightarrow m_2=-1 \\ \tan \theta =\frac{m_2-m_1}{1+m_1 m_2} \\ =\frac{-1-0}{1+(-1)(0)} \\ \tan \theta =-1 \\ =-\tan 45^{\circ} \\ =\tan \left(180^{\circ}-45^{\circ}\right) \\ =\tan 135^{\circ} \\ \Rightarrow \theta =135^{\circ}
(3,-1) तथा (4,-2) बिन्दुओं को मिलाने वाली रेखा की ढाल
Example:11.एक रेखा की ढाल दूसरी रेखा की ढाल का दुगुना है।यदि दोनों के बीच कोण की स्पर्शज्या (tangent) है तो रेखाओं की ढाल ज्ञात कीजिए।
Solution: m_1=2 m_2, \tan \theta=\frac{1}{3} \\ \tan \theta=\pm \frac{m_2-m_1}{1+m_1 m_2} \\ \Rightarrow \frac{1}{3}=\pm \frac{m_2-2 m_2}{1+2 m_2 \cdot m_2} \\ \Rightarrow \frac{1}{3}= \pm \left(\frac{-m_2}{1+2 m_2^2}\right)
धनात्मक चिन्ह लेने परः
1+2 m_2^2=-3 m_2 \\ \Rightarrow 2 m_2^2+3 m_2+1=0 \\ \Rightarrow 2 m_2^2+2 m_2+m_2+1=0 \\ \Rightarrow \left(m_2+1\right)\left(2 m_2+1\right)=0 \\ \Rightarrow \left(m_2+1\right)\left(2 m_2+1\right)=0 \\ \Rightarrow m_2=-1,-\frac{1}{2}
अतः m_1=-2,-1
ऋणात्मक चिन्ह लेने परः
1+2 m_2^2=3 m_2 \\ \Rightarrow 2 m_2^2-3 m_2+1=0 \\ \Rightarrow 2 m_2^2-2 m_2-m_2+1=0 \\ \Rightarrow \left(m_2-1\right)\left(2 m_2-1\right)=0 \\ \Rightarrow m_2=1,\frac{1}{2}
ढाल 1 और 2 या \frac{1}{2} और 1 या – 1 और – 2 या –\frac{1}{2} और – 1
Example:12.एक रेखा x_{1},y_{1} और (h,k) से जाती है।यदि रेखा की ढाल m है तो दिखलाइए k-y_1=m \left(h-x_1\right)
Solution:ढाल=\frac{y_2-y_1}{x_2-x_1} \\ \Rightarrow m=\frac{k-y_1}{h-x_1} \\ \Rightarrow k-y_1=m \left(h-x_1\right)
Example:13.यदि तीन बिन्दु (h,0),(a,b) और (0,k) एक रेखा पर हैं तो दिखाइए कि \frac{a}{h}+\frac{b}{k}=1
Solution:A(h,0),(a,b),(0,k)
AB की ढाल=BC की ढाल
\frac{b-0}{a-h}=\frac{k-b}{a-a} \\ \Rightarrow -a b=a k-a b-h k+b h \\ \Rightarrow h k=a k+b h \\ \Rightarrow \frac{a}{h}+\frac{b}{k}=1
Example:14.जनसंख्या और वर्ष के निम्नलिखित लेखाचित्र पर विचार कीजिए (आकृति)।रेखा AB की ढाल ज्ञात कीजिए और इसके प्रयोग से बताइए कि वर्ष 2010 में जनसंख्या कितनी होगी?
Solution:AB की ढाल m=\frac{y_2-y_1}{x_2 x_1} \\ \frac{97-92}{1995-1985}=\frac{5}{10}=\frac{1}{2}
माना 2010 में जनसंख्या=y
\frac{y-97}{2010-1995}=\frac{1}{2} \\ \Rightarrow y-97=\frac{15}{2} \\ \Rightarrow y=97+\frac{15}{2}=104.5 करोड़
उपर्युक्त उदाहरणों के द्वारा सरल रेखा कक्षा 11 (Straight Line Class 11),गणित में सरल रेखा (Straight Line In Mathematics) को समझ सकते हैं।
3.सरल रेखा कक्षा 11 के सवाल (Straight Line Class 11 Questions):
उस बिन्दु का बिन्दुपथ ज्ञात कीजिए जिसके निर्देशांक निम्नलिखित समीकरण द्वारा दिए गए हैंः
(1.) x=a \cos \theta, y=b \sin \theta जहाँ \theta चर राशि है।
(2.) x=a \sec \theta, y=b \tan \theta जहाँ \theta चर राशि है।
उत्तर (Answers):\text { (1.) } \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ \text { (2.) } \frac{x^2}{a^2}-\frac{y^2}{b^2}=1
उपर्युक्त सवालों को हल करने पर सरल रेखा कक्षा 11 (Straight Line Class 11),गणित में सरल रेखा (Straight Line In Mathematics) को ठीक से समझ सकते हैं।
Also Read This Article:-Arithmetic and Geometric Progression
4.सरल रेखा कक्षा 11 (Frequently Asked Questions Related to Straight Line Class 11),गणित में सरल रेखा (Straight Line In Mathematics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्न:1.वैश्लेषिक ज्यामिति का सर्वप्रथम अध्ययन किसने किया? (Who First Studied Analytical Geometry?):
उत्तर:द्विविमीय निर्देशांक ज्यामिति मुख्यतः बीजगणित और ज्यामिति का संयोजन है।बीजगणित के प्रयोग से ज्यामिति का क्रमबद्ध अध्ययन सर्वप्रथम प्रख्यात फ्रांसीसी दार्शनिक एवं गणितज्ञ Rene Descartes ने 1637 में प्रकाशित अपनी पुस्तक La Geometry में किया था।इस पुस्तक से ज्यामिति के अध्ययन में वक्र के समीकरण का विचार तथा सम्बन्धित वैश्लेषिक विधियों का प्रारम्भ हुआ।ज्यामिति एवं विश्लेषण का परिणाम संयोजन अब वैश्लेषिक ज्यामिति (Analytic Geometry) के रूप में उल्लेखित होता है।
प्रश्न:2.रेखा की ढाल किसे कहते हैं? (What is Slope of Line Called?):
उत्तर:यदि \theta किसी रेखा l का झुकाव है तो \tan \theta को रेखा l की ढाल कहते हैं।
प्रश्न:3.H. FREUDENTHAL के अनुसार ज्यामिति की परिभाषा क्या है? (What is Definition of Geometry According to H FREUDENTHAL?):
उत्तरःGeometry,as a logical system,is a means and even the most powerful means to make children feel the strength of the human spirit that is of their own spirit.
उपर्युक्त प्रश्नों के उत्तर द्वारा सरल रेखा कक्षा 11 (Straight Line Class 11),गणित में सरल रेखा (Straight Line In Mathematics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Straight Line Class 11
सरल रेखा कक्षा 11
(Straight Line Class 11)
Straight Line Class 11
सरल रेखा कक्षा 11 (Straight Line Class 11) बिन्दुओं का समुच्चय है,अतः दो बिन्दुओं
के बीच दूरी को रेखा या सरल रेखा कहते हैं। रेखा की ढाल (Slope of a Line):
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.