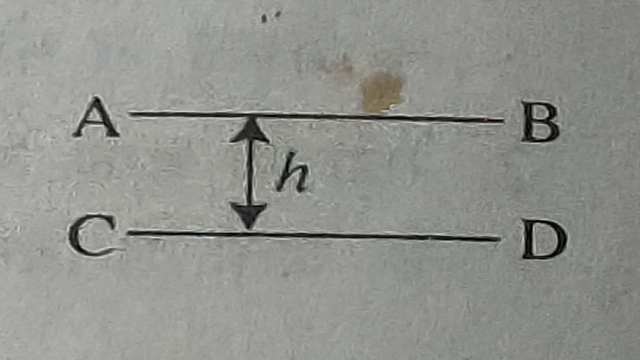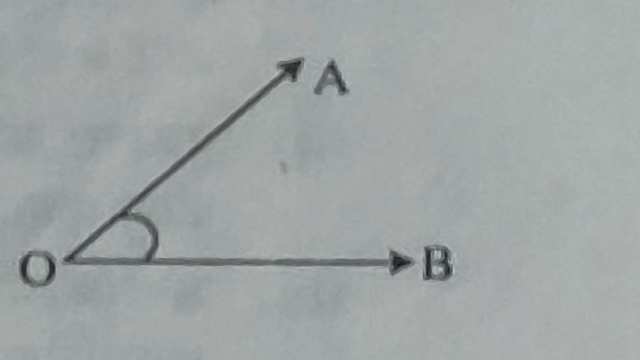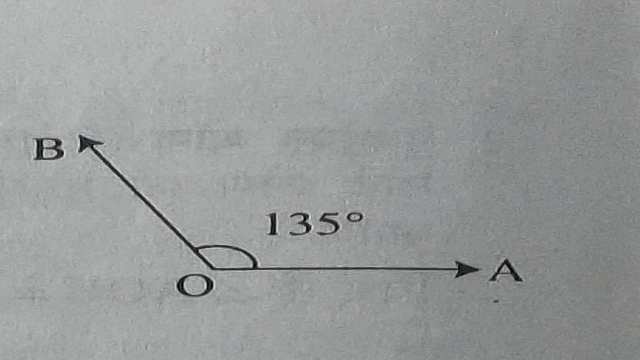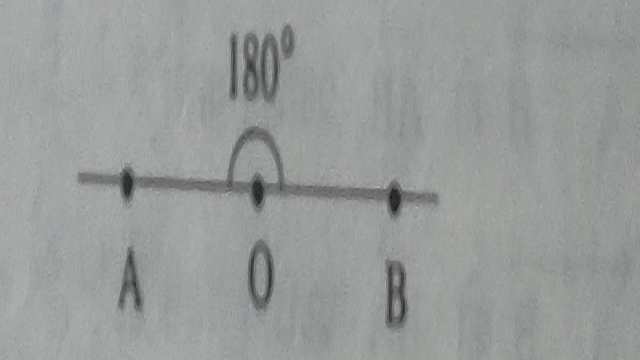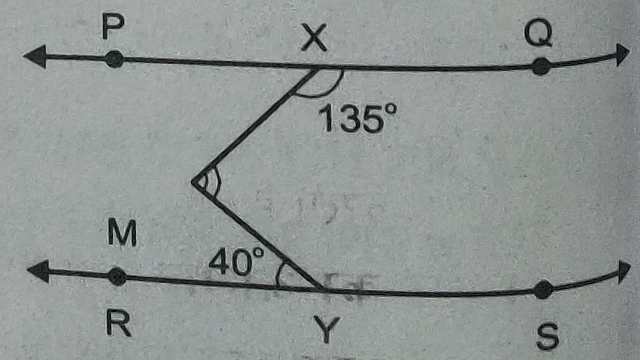1.कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9), रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9)-

कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9) में कोण के प्रकार,एक बिन्दु पर बननेवाले कोण,दो रेखाओं के साथ तिर्यक रेखा द्वारा बनाए गए कोणों का अध्ययन किया जाता है।
(A) रेखाएं और कोण (Lines and Angles)-
(1.)बिन्दु (Point)-बिन्दु एक ऐसी वस्तु है जो अपरिभाषित है जिसकी न लम्बाई होती है,न चौड़ाई होती है और न मोटाई होती है जिसका स्वरूप है (.) है।
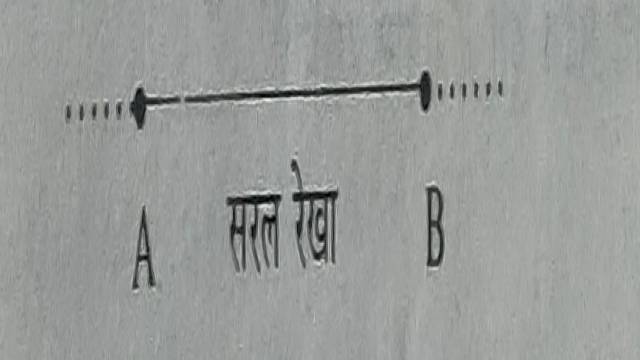
(2.)रेखा या सरल रेखा (Line or Straight Line)-कोई सरल रेखा बिन्दुओं का समुच्चय है।अतः दो बिन्दुओं के बीच की दूरी को रेखा या सरल रेखा कहते हैं।
रेखा को अंग्रेजी के अक्षर l,m,n,…से प्रदर्शित करते हैं या द्वारा प्रदर्शित करते हैं या रेखा AB कहते हैं।
(3.)एक सरल रेखा पर अनन्त बिन्दु होते हैं।
(4.)एक बिन्दु से अनन्त रेखाएं खींची जा सकती हैं।
(5.)दो विभिन्न बिन्दुओं से एक और केवल एक सरल रेखा खींची जा सकती है।
(6.)एक रेखा पर आनेवाले बिन्दु संरेख कहलाते हैं।
(7.)एक बिन्दु से जानेवाली सभी रेखाएं संगामी कहलाती हैं।
(8.)किसी रेखा PQ पर बिन्दु A व B लें तो उनके बीच की दूरी रेखाखण्ड कहलाती है जिसे से प्रदर्शित करते हैं।
(9.)तीर की दिशा के अनुसार नाम देने पर रेखा किरण कहलाती है जैसे A\rightarrow B को \underset{AB} {\rightarrow}
(10.)प्रत्येक रेखाखण्ड की निश्चित लम्बाई होती है।
(11.)यदि दो रेखाखण्ड एवं एक ही लम्बाई के हों तो सर्वांगसम कहे जाते हैं।
(11.)वक्र रेखा (Curved Line)-वह रेखा जो सीधी न होकर वक्राकार या टेढ़ी-मेढ़ी होती है।वक्र रेखा कहलाती है।

(13.)क्षैतिज रेखा (Horizontal Line)-वह रेखा जो पृथ्वी के धरातल के समान्तर होती है।लेटी हुई रेखा या क्षैतिज रेखा कहलाती है।

(14.)समान्तर रेखाएं (Parallel Lines)-वे रेखाएं जिनके बीच की दूरी सदैव समान रहती है।समान्तर रेखाएं कहलाती हैं।समान्तर रेखाएं आपस में कभी भी प्रतिच्छेद नहीं करती हैं।चित्र में AB व CD समान्तर रेखाएं हैं।इनके बीच दूरी समान रहती है।

(15.)असमान्तर रेखाएं (Converging Lines)-वे रेखाएं जिनके बीच समान अन्तर नहीं होता और आगे बढ़ाने पर मिल जाती हैं या प्रतिच्छेद हो जाती हैं।चित्र में AB व CD असमान्तर रेखाएं हैं।

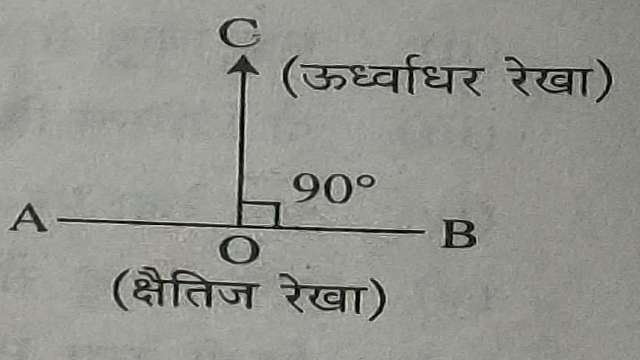
(16.)उर्वाध्वर रेखाएं (Verical Lines)-ये रेखाएं पृथ्वी के धरातल के लम्बवत होती हैं। इन्हें खड़ी रेखाएं भी कहते हैं।चित्र में AB क्षैतिज और CD उर्ध्वाधर रेखाएं हैं।

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Properties of Triangles class 9

2.एक बिन्दु पर बनने वाले कोण (Angles at a Point), रेखाएं और कोण (Lines and Angles),रेखा और कोण (Line and Angles)-

कोण एवम् उसका मापन:
कोण (Angle): कोई भी दो किरणें जिनका आदि बिन्दु एक ही हो,कोण बनाती हैं।
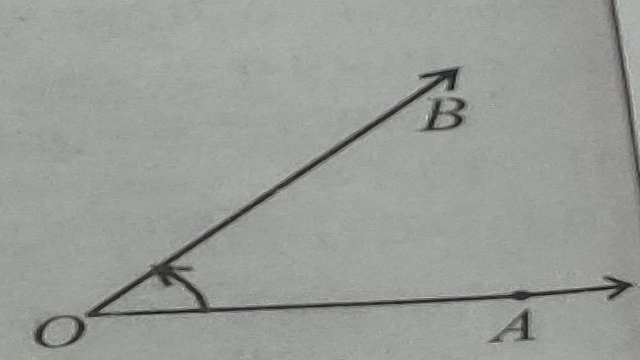
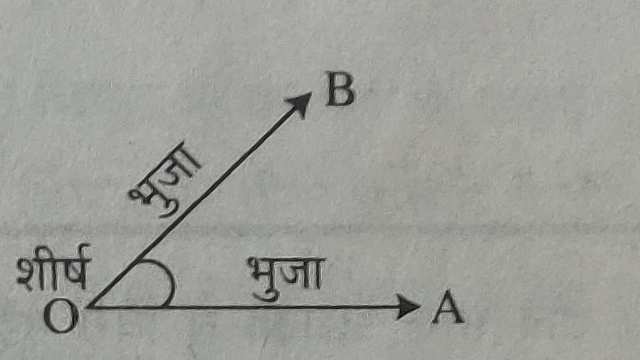
सामने आकृति में एक ही आदि बिन्दु O से दो किरणें \underset{OA} {\rightarrow} तथा \underset{OB} {\rightarrow} निकल रही हैं और आकृति AOB और BOA बना रही है।इस आकृति को बिन्दु O पर बनने वाला कोण कहते हैं और इसे \angle AOB \text { या } \angle BOA लिखा जाता है।

किरणे \underset{OA} {\rightarrow} तथा \underset{OB} {\rightarrow} (जो कि कोण बनाती हैं) \angle AOB \text { या } \angle BOA की भुजाएं कहलाती हैं। उभयनिष्ठ बिन्दु O को कोण का शीर्ष कहते हैं।
कभी-कभी सुविधा के लिए कोण के भीतर कोई अंक या अक्षर लिखकर भी कोण को व्यक्त करते हैं।जैसे सामने की आकृति में  \angle 1 \text { तथा } \angle x दर्शाएं गए हैं।

कोण का माप:
माना कि परिक्रामी रेखा एक बिन्दु O के सापेक्ष OA स्थिति से परिक्रमण कर OB स्थिति में आ जाती है तो इस परिक्रमण को \angle AOB  का परिमाण कहते हैं।

यदि रेखा OA बिन्दु O के चारों ओर एक पूरा चक्कर लगाकर अपनी पूर्व स्थिति OA पर आ जाए तो इस प्रकार बने कोण के परिमाण को 360 बराबर भागों में बांटकर इसे 360 अंश (डिग्री) द्वारा व्यक्त किया जाता है।
इस प्रकार एक 1 भाग=1 अंश=1° एवम् 360 भाग=360 अंश=360°
यदि एक अंश को 60 बराबर भागों में बांटा जाए तो ऐसे प्रत्येक भाग को 1 कला (1 मिनट) कहते हैं।इसी प्रकार 1 कला को भी 60 भागों में बांटने पर प्रत्येक भाग को एक विकला (सैकण्ड) कहा जाता है।सांकेतिक रूप में एक डिग्री,एक मिनट तथा सैकण्ड को क्रमशः 1°,1′ तथा 1″ से व्यक्त करते हैं।
अतः 1°=60 कला (मिनट)=60′
1 कला (मिनट)=60 विकला (सैकण्ड) अर्थात् 1°=68″
कोण मापने के लिए चांदे का उपयोग करते हैं, इसमें 0° से 180° तक के निशान होते हैं।

3.कक्षा 9 के लिए रेखाएं और कोणों का वर्गीकरण (Classification of Lines and Angles for Class 9)-

(1.)न्यून कोण (Acute Angle):वह कोण जिसका माप 0° से अधिक एवं 90° से न्यून हो।चित्र में \angle AOB एक न्यून कोण है।

(2.)समकोण (Right Angle):वह कोण जिसका माप 90° हो।चित्र में \angle POR एक समकोण है।
एक समकोण= \frac {1}{4} एक पूर्ण चक्कर
एक समकोण की स्थिति में एक रेखा दूसरी पर ठीक खड़ी होती है।

(3.)अधिक कोण (Obtuse Angle):वह कोण जिसका परिणाम 90° से अधिक परन्तु 180° से कम होता है।चित्र में \angle LMN एक अधिक कोण है।

(4.)सरल कोण ऋजु कोण (Straight Angle):वह कोण जिसका परिणाम 180° हो उसे सरल कोण या ऋजु कोण कहते हैं।

आकृति में \angle AOB एक सरल कोण है।सरल कोण में कोण की भुजाएं एक सरल रेखा में,एक दूसरे से विपरीत ओर स्थित होती है।
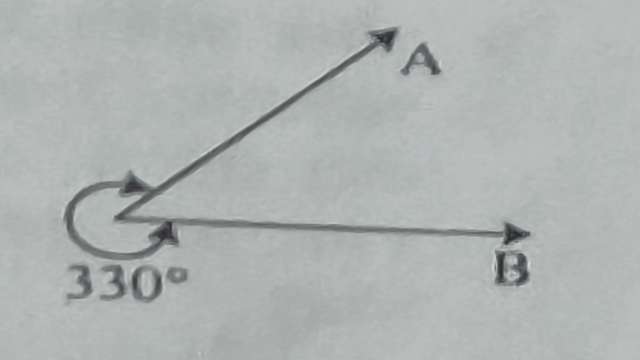
(5.)वृहत कोण,पुनर्युक्त कोण (Reflex Angle):वह कोण जिसका परिणाम 180° से अधिक परन्तु 360° से कम हो। आकृति में \angle ABC एक वृहत कोण है।

(6.)आसन्न कोण (Adjacent Angle):ऐसे दो कोण जिनमें
(i) शीर्ष उभयनिष्ठ हो
(ii)एक भुजा उभयनिष्ठ हो
(iii) कोणों की अन्य भुजाएं,उभयनिष्ठ भुजा के विपरीत ओर हों।आसन्न कोण कहलाते हैं।

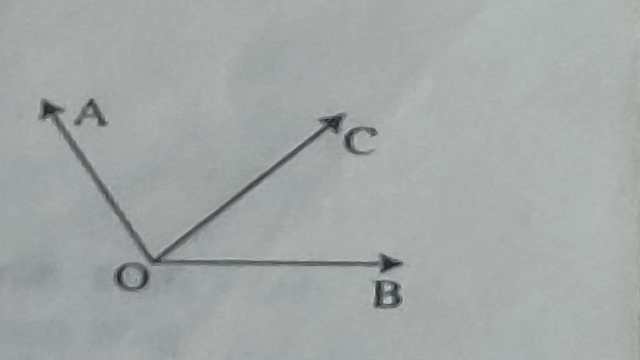
सामने आकृति में \angle AOB \text { तथा  } \angle COB आसन्न कोण हैं। इनमें शीर्ष O एवम् भुजा उभयनिष्ठ है। भुजाएं OA तथा OC उभयनिष्ठ भुजा के विपरीत ओर है।
(7.)सम्पूरक कोण (Supplementary Angles):यदि दो कोणों के माप का योगफल 180° के बराबर हो तो वे एक-दूसरे के संपूरक कोण कहलाते हैं।जैसे 140°तथा 40°,105° तथा 75°,30° तथा 150° आदि।
ऐसे आसन्न कोणों को जिनके कोणों का माप योग 180° हो उन्हें आसन्न सम्पूरक कोण कहते हैं। सामने दी गई आकृति में \angle AOC \text { एवम्  } \angle BOC आसन्न सम्पूरक कोण हैं।

(8.)पूरक कोण (Complementary Angles):यदि दो कोणों के मापों का योगफल 90° के बराबर हो तो उन्हें एक-दूसरे का पूरक कोण कहा जाता है।
उदाहरणार्थ:52° तथा 38°,67° तथा 23° माप वाले कोण पूरक कोण हैं। अतः 10° का पूरक कोण= 90°-10°=80°
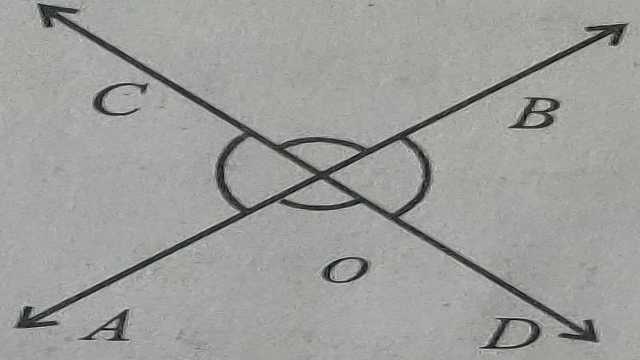
(9.)शीर्षाभिमुख कोण (Vertically Opposite Angles):यदि दो रेखाएं एक दूसरे को प्रतिच्छेद करें तो प्रतिच्छेद बिन्दु पर एक-दूसरे के विपरीत बने कोण,शीर्षाभिमुख कोण कहलाते हैं।आकृति में AB एवम् CD एक-दूसरे को O बिन्दु पर प्रतिच्छेद कर रही हैं और इस प्रकार बिन्दु O पर बने कोण \angle AOC \text { तथा } \angle BOD , \angle AOD  \text { तथा } \angle BOC शीर्षाभिमुख कोण हैं।शीर्षाभिमुख कोण युग्म में कोणों की भुजाएं परस्पर विपरीत किरणें होती हैं।

( 10.)एक बिन्दु के चारों ओर बनने वाले कोण अर्थात् पूर्ण कोण (Complete Angle)-एक बिन्दु पर बना कोण अर्थात् 360° के कोण को पूर्ण कोण (Complete Angle) कहते हैं।

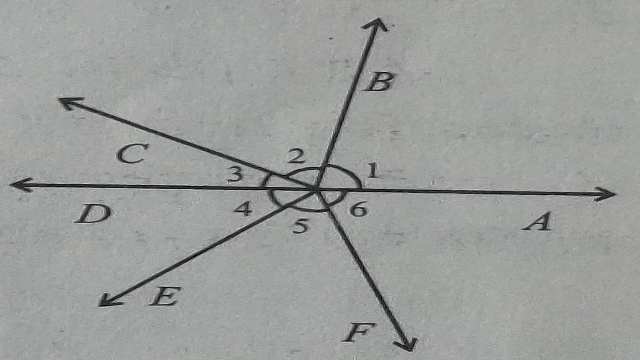
यदि एक बिन्दु से विभिन्न किरणें निकले तो इस प्रकार प्राप्त कोणों को एक बिन्दु के चारों ओर बने कोण कहा जाता है।जैसा कि कोण मापन में बताया गया है कि परिक्रामी रेखा द्वारा एक बिन्दु के चारों ओर पूरे एक परिक्रमण से बना कोण 360° के बराबर होता है।
अर्थात् \angle 1 + \angle 2 +\angle 3 + \angle 4 +\angle 5 + \angle 6=360°  है।
(11.)यदि कोई किरण किसी रेखा पर आधारित हो तो इस प्रकार बने दो आसन्न कोणों का योग 180° होता है।
(12.)यदि आसन्न कोणों का योग 180° हो तो उनकी बाह्य भुजाएं एक ही सरल रेखा में होती हैं।
(13.)यदि दो रेखाएं प्रतिच्छेद करें तो शीर्षाभिमुख कोण समान होते हैं।
(14.)यदि दो परस्पर प्रतिच्छेदी रेखाओं से बने कोणों में से एक समकोण हो तो प्रत्येक कोण समकोण होता है।
(15.)निम्नांकित कोण में

‘O’ उभयनिष्ठ बिन्दु को शीर्ष कहते हैं तथा प्रत्येक किरण को भुजा कहते हैं।
(16.)यदि दो कोणों की माप बराबर हो तो दोनों कोण सर्वांगसम होंगे जैसे-
इसे चिन्ह \cong से प्रदर्शित करते हैं। अतः

\angle ABC \cong  \angle DEF

कोणों का रैखिक युग्म (A linear pair of angles):
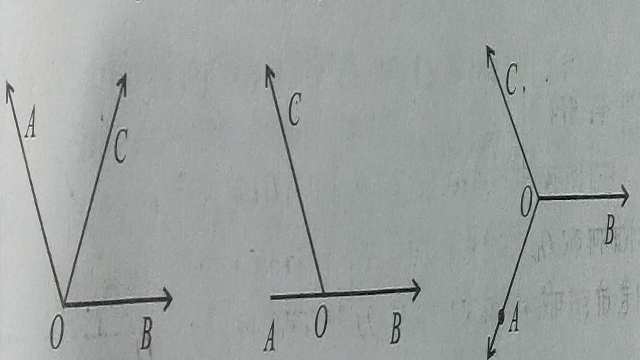
नीचे दी गई आकृतियों में दिए गए कोण युग्मों को ध्यान से देखों
प्रत्येक कोण युग्म ( \angle AOC \text { तथा  } \angle BOC ) आसन्न कोण हैं। इनमें बीच की आकृति में अंकित कोण युग्म ऐसे हैं कि इनके मापों का योगफल 180° के बराबर है।ऐसे कोण युग्म को “रैखिक कोण युग्म” कहते हैं। स्पष्ट है कि एक रैखिक कोण युग्म में आसन्न कोण संपूरक होते हैं।

परिभाषा (Definition);दो आसन्न कोणों को जिनकी उभयनिष्ठ भुजा के अतिरिक्त भुजाएं,दो विपरीत किरणें हों, कोणों का रैखिक युग्म कहते हैं।
रैखिक कोण-युग्म अभिगृहीत-
इस प्रकार हम देखते हैं कि आसन्न कोणों में यदि:
(i) कोणों की बाह्य भुजाएं दो विपरीत किरणें हों अर्थात् वे एक रेखा में हों तो कोणों के मापों का योगफल 180° के बराबर होता है।
(या एक रेखा पर किरण का सिरा स्थित हो तो आसन्न कोणों का योग 180° होता है)
(ii) कोणों का मापों का योगफल 180° के बराबर हो तो कोणों की बाह्य भुजाएं दो विपरीत किरणें होती हैं अर्थात् वे एक ही रेखा में होती है।
इसी ज्यामितीय तथ्य को एक अभिगृहीत मान लेते हैं और इसे कोणों का रैखिक युग्म अभिगृहीत कहते हैं।इसे निम्न प्रकार से भी व्यक्त कर सकते हैं-
दो आसन्न कोण एक रैखिक कोण युग्म होते हैं यदि और केवल यदि वे सम्पूरक होते हैं।
प्रमेय (Theorem):यदि दो सरल रेखाएं परस्पर प्रतिच्छेद करें तो शीर्षाभिमुख कोण बराबर होते हैं।
दिया है (Given): रेखाएं AB एवं CD जो एक दूसरे को बिन्दु O पर प्रतिच्छेद कर रही है।
सिद्ध करना है (To Prove):शीर्षाभिमुख कोण

\angle AOC = \angle DOB \text { एवं } \angle AOD= \angle BOC

उपपत्ति (Proof):किरण OD का प्रारम्भिक बिन्दु O,रेखा AB पर स्थित है।

\therefore \angle AOD + \angle DOB=180°
(रैखिक कोण-युग्म अभिगृहीत से)………….(1)
इसी प्रकार \angle AOC + \angle AOD=180°…..(2)
(रैखिक कोण-युग्म अभिगृहीत से)
समीकरण (1) व ( 2) से-

\Rightarrow  \angle AOC + \angle AOD=\angle AOD + \angle DOB \\ \Rightarrow  \angle AOC=\angle DOB
इसी प्रकार सिद्ध कर सकते हैं कि

\angle AOD=\angle BOC (Hence Proved)
उपप्रमेय (Corollary):1.यदि दो सरल रेखाएं एक-दूसरे को प्रतिच्छेद करें तो प्रतिच्छेद बिन्दु पर बनने वाले सभी कोणों का योगफल 360° के बराबर होता है।
उपप्रमेय (Corollary):2.शीर्षाभिमुख कोणों के अर्द्धक एक सरल रेखा में होते हैं।

4.दो रेखाओं के साथ तिर्यक रेखा द्वारा बनाए गए कोण (Angles drawn by intersecting line with two lines),समानांतर रेखाओं में कोणों के प्रकार (Types of angles in parallel lines)-

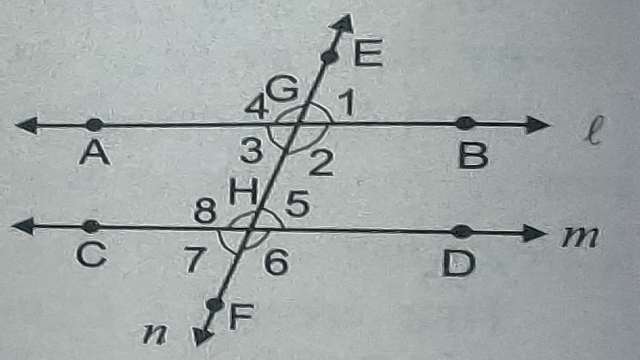
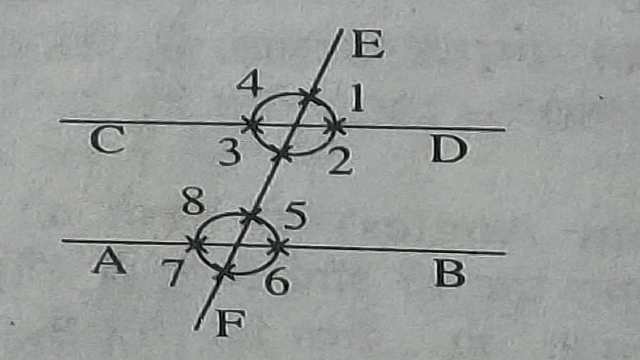
आकृति में AB तथा CD दो रेखाएं हैं एवम् एक रेखा EF उन्हें क्रमशः G तथा H बिन्दुओं पर काटती हैं।ऐसी सरल रेखा को जो दो या अधिक सरल रेखाओं को अलग-अलग बिन्दुओं पर काटे,उनकी तिर्यक रेखा कहते हैं। यहां रेखा EF तिर्यक रेखा है।
यहां आकृति में तीन रेखाएं कुल आठ कोण बनाती हैं।बिन्दु G पर चार कोण \angle 1 , \angle 2 ,\angle 3  \text { एवम्  } \angle 4 बन रहे हैं।बिन्दु H पर भी चार कोण \angle 5 , \angle 6 ,\angle 7  \text { एवम्  } \angle 8 बन रहे हैं।

यदि AB और CD समान्तर हों तो इन कोणों के मध्य निम्न सम्बन्ध होते हैं-
(1.)संगत कोण (Corresponding Angle): निम्नलिखित कोण युग्मों को संगत कोण कहते हैं जो आपस में बराबर होते हैं।

\angle 1 =\angle 5,\angle 2 =\angle 6,\angle 3 =\angle 7,\angle 4 =\angle 8
(2.)एकान्तर कोण (Alternate Angle): \angle 2 =\angle 8,\angle 3 =\angle 5 को एकान्तर कोण कहते हैं जो आपस में बराबर होते हैं।
(3.)अन्त:कोण (Interior Opposite Angles)-तिर्यक रेखा के एक ही ओर स्थित कोण अन्त:कोण कहलाते हैं। दोनों अन्त: कोणों का योग 180° होता।

\angle 2 +\angle 5=\angle 3 +\angle 8=180°
(4.)बहिष्कोण (Interior Opposite Angles)-\angle 1 , \angle 4 \text { तथा } \angle 6 , \angle 7 को बहिष्कोण कहते हैं। दोनों बहिष्कोणों का योग 180° होता है।

\angle 1 + \angle 4= \angle 6 + \angle 7=180°
प्रमेय (Theorem):2.यदि दो समान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे तो एकान्तर कोण बराबर होते हैं।
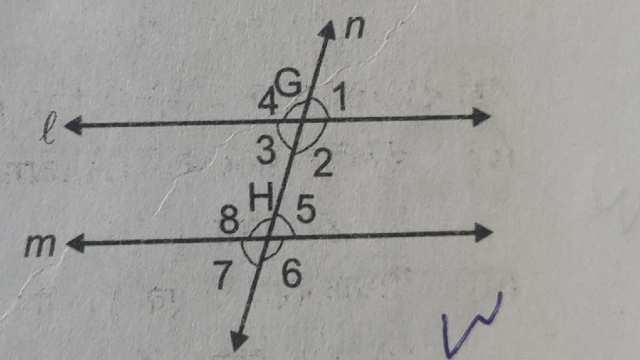
दिया है (Given):दो समान्तर रेखाएं l तथा m हैं जिन्हें n तिर्यक रेखा क्रमशः G तथा H बिन्दुओं पर प्रतिच्छेद करती है।इस प्रकार एकान्तर कोण युग्म (\angle 2,\angle 1) \text { तथा } (\angle 3,\angle 4)बनते हैं।
सिद्ध करना है (To Prove): \angle 1=\angle 2 \text { एवं  } \angle 3=\angle 4

उपपत्ति (Proof): यहां \angle 2=\angle 6(शीर्षाभिमुख कोण)…(1)
एवं \angle 1=\angle 6 (संगत कोण अभिगृहीत से)…..(2)
समीकरण (1) व (2) से-

\Rightarrow \angle 1=\angle 2
इसी प्रकार \angle 4=\angle 5 (संगत कोण अभिगृहीत से)
एवं \angle 3=\angle 5 (शीर्षाभिमुख कोण)
अतः समीकरण (3) व (4) से-
\Rightarrow \angle 3=\angle 4 (Hence Proved)
प्रमेय (Theorem):3.(प्रमेय 2 का विलोम):यदि दो सरल रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे और इस प्रकार बने एकान्तर कोण प्रतिच्छेद करे और इस प्रकार बने एकान्तर कोण बराबर हों तो रेखाएं समान्तर होती है।
दिया है (Given):l तथा m दो रेखाएं जिनको तिर्यक रेखा क्रमशः G तथा H बिन्दुओं पर प्रतिच्छेद करती है। एकान्तर कोण \angle 2=\angle 8 \text { तथा  } \angle 3=\angle 8 है।
सिद्ध करना है (To Prove):l \parallel m

उपपत्ति (Proof): यहां \angle 1=\angle 3 (शीर्षाभिमुख कोण)……(1)
एवं \angle 3=\angle 5 (दिया है)…..(2)
समीकरण (1)‌ व (2) से-

\Rightarrow \angle 1=\angle 5
अतः संगत कोण अभिगृहीत से 

\Rightarrow l \parallel m
प्रमेय (Theorem):4.यदि दो समान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे तो एक ओर के अन्त: कोणों का योग दो समकोण होता है।
दिया है (Given):l तथा m दो समान्तर रेखाएं हैं जिन्हें तिर्यक रेखा n क्रमशः G तथा H बिन्दुओं पर प्रतिच्छेद करती है।बिन्दुओं G तथा H पर क्रमशः कोण \angle 1 , \angle 2 ,\angle 3 ,  \angle 4 \text  { तथा }  \angle 5 , \angle 6 ,\angle 7 , \angle 8 बन रहे हैं।अन्त: कोण युग्म \angle 2 ,\angle 5 \text { एवं  } \angle 3 ,\angle 8 हैं।
सिद्ध करना है (To Prove): \angle 2 + \angle 5 =180° एवं \angle 3 + \angle 8 =180°

उपपत्ति (Proof): यहां \angle 1 + \angle 2 =180° (रैखिक कोण युग्म से)……(1)
एवं \angle 1 = \angle 5 (संगत कोण अभिगृहीत से)…..(2)
समीकरण (1) व (2) से-

\angle 2 + \angle 5 =180°
इसी प्रकार \angle 3 + \angle 4 =180° (रैखिक कोण युग्म से)……(3)
\angle 4 = \angle 8 (संगत कोण अभिगृहीत से)…………(4)
अतः समीकरण (3) एवं (4) से-
\angle 3 + \angle 8 =180° (Hence Proved)
प्रमेय (Theorem):5.(प्रमेय 4 का विलोम):यदि दो सरल रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे और तिर्यक रेखा के एक ही ओर बने अन्त: कोणों का योग समकोण हो तो वे रेखाएं समान्तर होंगी।
दिया है (Given):l तथा m दो रेखाएं हैं जिन्हें तिर्यक रेखा n क्रमशः G एवं H बिन्दुओं पर प्रतिच्छेद करती है।इस प्रकार बिन्दु G एवं H पर क्रमशः \angle 1 , \angle 2 ,\angle 3 ,  \angle 4 \text { एवं } \angle 5 , \angle 6 ,\angle 7  ,\angle 8  बन रहे हैं। अन्त: कोण \angle 2 + \angle 5 =180° \text { तथा } \angle 3 + \angle 8 =180°
सिद्ध करना है (To Prove):l \parallel m

उपपत्ति (Proof): यहां \angle 1 + \angle 2 =180°(रैखिक कोण युग्म)
एवं \angle 2 + \angle 5=180° (दिया है)
समीकरण (1) व (2) से-

\angle 1 = \angle 5
अतः संगत कोण अभिगृहीत से- l \parallel m
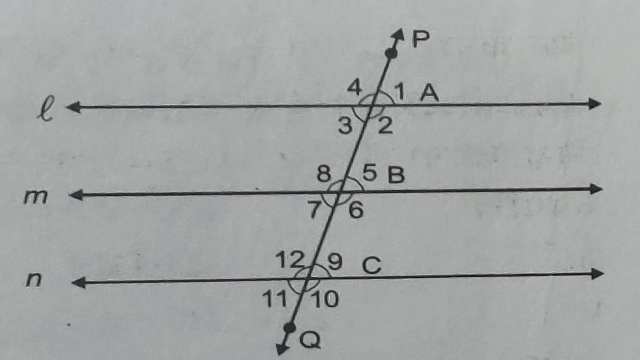
प्रमेय (Theorem):6.यदि दो सरल रेखाएं किसी तीसरी सरल रेखा के समान्तर हो तो दोनों भी परस्पर समान्तर होंगी।
दिया है (Given):l \parallel n \text { तथा } m \parallel n हैं।
रचना (Construction) : l \parallel m एक तिर्यक रेखा PQ खींची जो l,m तथा n को A,B तथा C पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove):l \parallel m

उपपत्ति (Proof): l \parallel n एवं PQ तिर्यक रेखा है
अतः \angle 1 = \angle 9 (संगत कोण अभिगृहीत से)………(1)
m \parallel n एवं PQ तिर्यक रेखा है
अतः \angle 5 = \angle 9 (संगत कोण अभिगृहीत से)……..(2)
समीकरण (1) व (2) से-

\angle 1 = \angle 5…..(3)
\angle 1 \text { तथा }  \angle 5, l व m पर बने संगत कोण है अतः संगत कोण अभिगृहीत से l \parallel m है।

5.कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9 Examples),रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9 Examples), लाइनें और कोण कक्षा 9 सवाल और जवाब (Lines and Angles class 9 Questions and Answers)-

Example-1.(2x+4) एवं (x-1) अंश माप के कोण रैखिक कोण युग्म हैं, इन्हें ज्ञात कीजिए।
Solution-2x+4+x-1=180° (रैखिक कोण युग्म हैं)
\Rightarrow  3x+3=180 \\ \Rightarrow  3x=177 \\ \Rightarrow  x=\frac {177}{3} \\ \Rightarrow  x=59 \\ 2x+4=2(59)+4=118+4=122° \\ x-1=59-1=58°
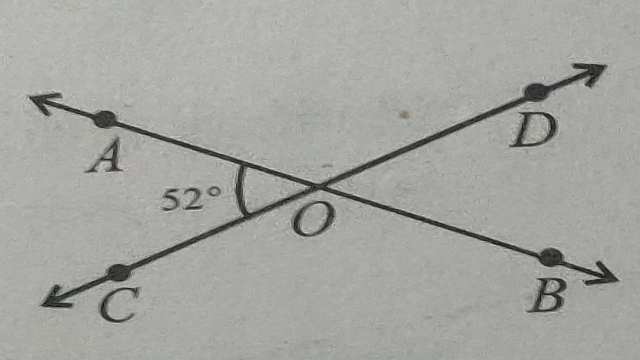
Example-2.चित्र से

(i) \angle BOD का माप बताइए।
(ii) \angle AOD का माप बताइए।
(iii)शीर्षाभिमुख कोण युग्म कौन-कौन से हैं?
(iv) \angle AOC के आसन्न संपूरक कोण कौन-कौन से हैं?बताइए।
Solution-(i)\angle BOD= \angle AOC (शीर्षाभिमुख कोण हैं)

\angle BOD =52°
(ii) \angle AOC + \angle AOD = 180° (रैखिक कोण युग्म से) 

52° +\angle AOD = 180° \\  \angle AOD = 180°-52° \\  \angle AOD = 128°
(iii) \angle AOD \text { व  } \angle BOC  \text { तथा  } \angle AOC  \text { व }  \angle BOD शीर्षाभिमुख कोण युग्म हैं।
(iv) \angle AOC के आसन्न सम्पूरक कोण \angle AOD \text { व  } \angle BOC हैं।
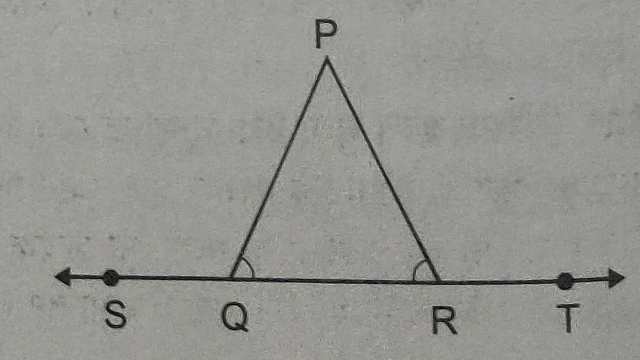
Example-3.दिए गए चित्र में यदि \angle PQR= \angle PRQ है तो सिद्ध कीजिए कि \angle PQS= \angle PRT

Solution-दिया है (Given): \angle PQR= \angle PRQ
सिद्ध करना है (To Prove):\angle PQS= \angle PRT
उपपत्ति (Proof): \angle PQS + \angle PQR=180° (रैखिक कोण युग्म से)….(1)
\angle PRT + \angle PRQ=180° (रैखिक कोण-युग्म से)…..(2)
समीकरण (1) व (2) से-
\angle PQS +  \angle PQR =\angle PRT + \angle PRQ........(3) \\  \angle PQR= \angle PRQ (दिया है) …………(4)
समीकरण (4) से (3) में मान रखने पर-

\Rightarrow  \angle PQS +  \angle PRQ =\angle PRT + \angle PRQ \\ \Rightarrow  \angle PQS  =\angle PRT
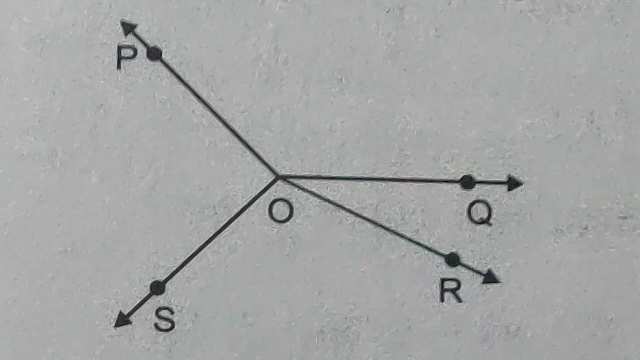
Example-4.चित्र में OP,OQ,OR और OS चार किरणें हैं। सिद्ध कीजिए कि \angle POQ+ \angle QOR + \angle SOR + \angle POS=360° है।

Solution-दिया है (Given):OP,OQ,OR और OS चार किरणें हैं।
सिद्ध करना है (To Prove):\angle POQ+ \angle QOR + \angle SOR + \angle POS=360°
रचना (Construction):OQ को T तक बढ़ाया।
उपपत्ति (Proof):\angle POT + \angle POQ=180° (रैखिक कोण युग्म से)…………(1)
\angle TOS + \angle SOR + \angle QOR=180° (रैखिक कोण-युग्म से)………..(2)
समीकरण (1) व (2) को जोड़ने पर-

\angle POT + \angle POQ +\angle TOS + \angle SOR + \angle QOR=360° \\  \Rightarrow (\angle POT + \angle TOS  )+ \angle POQ + \angle SOR + \angle QOR=360° \\ \Rightarrow \angle POQ+ \angle QOR + \angle SOR + \angle POS=360°
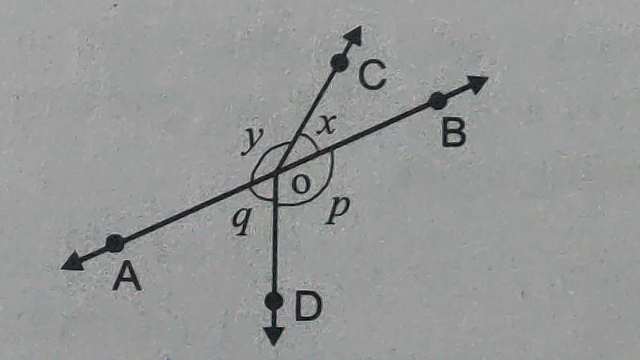
Example-5.चित्र में यदि \angle x + \angle y=\angle p + \angle q है तो सिद्ध कीजिए कि AOB एक सरल रेखा है।

Solution-दिया है (Given): \angle x + \angle y=\angle p + \angle q
सिद्ध करना है (To Prove):AOB एक सरल रेखा है।
उपपत्ति (Proof): \angle AOC + \angle BOC +\angle AOD + \angle BOD =360° \\ \angle x + \angle y+\angle p + \angle q =360°.....(1)
(एक बिन्दु पर बनने वाले कोणों का योग)

\angle x + \angle y=\angle p + \angle q (दिया है)
समीकरण (2) से (1) में मान रखने पर-

\Rightarrow  \angle p + \angle q+\angle p + \angle q =360° \\ \Rightarrow  2(\angle p + \angle q )=360° \\ \Rightarrow \angle p + \angle q =\frac {360°}{2} \\ \Rightarrow \angle p + \angle q =180°
अतः रैखिक कोण युग्म से AOB एक सरल रेखा है।
Example-6.AP और BQ उन दो एकान्तर कोणों के समद्विभाजक हैं जो समान्तर रेखाओं l और m को तिर्यक रेखा n द्वारा प्रतिच्छेद से बनते हैं दर्शाइए कि AP \parallel BQ है।

Solution-दिया है (Given):AP और BQ एकान्तर कोणों के समद्विभाजक हैं।तथा l \parallel m
सिद्ध करना है (To Prove): AP \parallel BQ
उपपत्ति (Proof):l \parallel m (दिया है)
तथा तिर्यक रेखा n इनको काटती है।
अतः \angle FAB=\angle ABD (एकान्तर कोण) 
(BQ व AP एकान्तर कोण के समद्विभाजक हैं)
ये कोण एकान्तर कोण हैं व समान है तथा AB तिर्यक रेखा काटती है।
अतः AB \parallel BQ
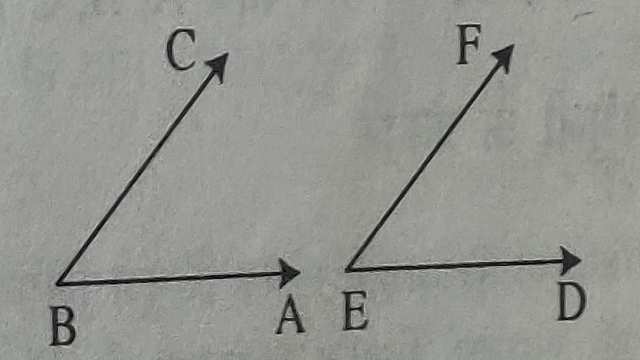
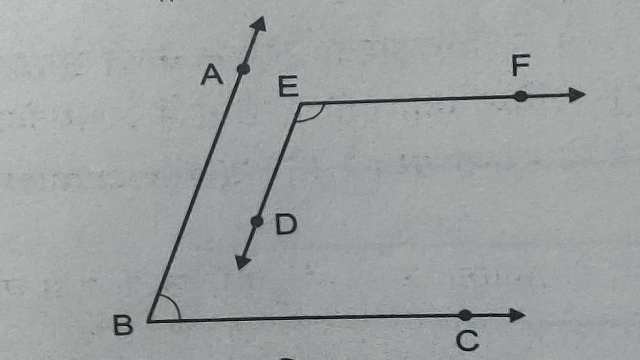
Example-7.चित्र में BA \parallel ED \text { और } BC \parallel EF है।दर्शाइए कि \angle ABC + \angle DEF =180° है।

Solution-दिया है (Given):BA \parallel ED \text { व } BC \parallel EF
सिद्ध करना है (To Prove):\angle ABC + \angle DEF =180°
रचना (Construction):DE को आगे बढ़ाया जो BC को G पर काटती है।
उपपत्ति (Proof):EF \parallel BC(दिया है)
अतः \angle EGC + \angle DEF =180°(अन्त: कोणों का योग)
AB \parallel DE(दिया है)…………(1)
अतः \angle ABC = \angle EGC  (संगत कोण)………..(2)
समीकरण (1) व (2) से-

\angle ABC + \angle DEF =180°
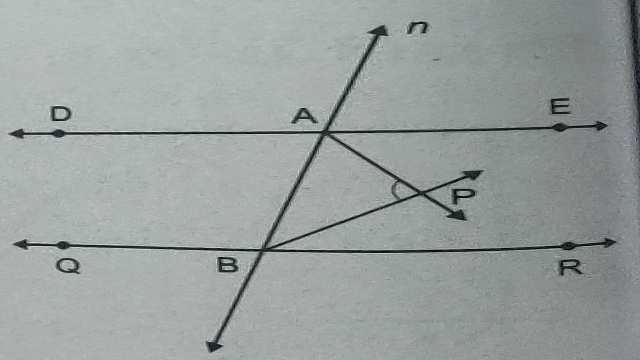
Example-8.चित्र में DE \parallel QR तथा AP और BP क्रमशः \angle EAB \text { और } \angle RBA के समद्विभाजक हैं।\angle APB का मान ज्ञात कीजिए।

Solution–DE \parallel QR तथा तिर्यक रेखा n इनको काटती है।
अतः \angle EAB + \angle RBA =180° (अन्त: कोणों का योग)
\Rightarrow  \frac {1} {2} \angle EAB + \frac {1} {2} \angle RBA =\frac {1} {2} \times 180° \\ \Rightarrow   \angle PAB +  \angle ABP =90°(\because AP व BP समद्विभाजक हैं)……..(1)

\triangle ABP \text { में } \\ \angle APB +\angle PAB + \angle ABP=180° \\ \angle APB +90°=180° [(1) से  ] \\ \Rightarrow \angle APB =90°
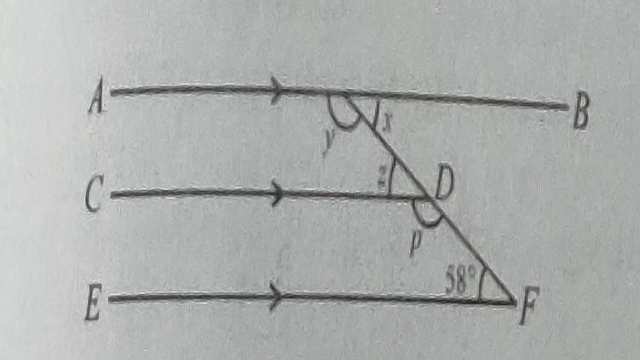
Example-9.चित्र में AB \parallel CD,CD \parallel EF और y:z=3:7 है तो x का मान ज्ञात कीजिए।

Solution– CD \parallel EF तथा PQ तिर्यक रेखा काटती है
अतः \angle DOQ + \angle FQO=180°(अन्त: कोणों का योग)
\angle POC = \angle DOQ (शीर्षाभिमुख कोण)

\angle y = \angle DOQ.............(2)
समीकरण (1) व (2) से-

\angle y + \angle z=180°........(3) \\ y:z=3:7
माना y=3t,z=7t \\ 3t+7t=180° \\ \Rightarrow  10t=180° \\ \Rightarrow  t=18°
अतः y=3 \times 18°= 54° \\ AB \parallel CD
अतः \angle x + \angle y=180° \text { (अन्त: कोणों का योग) } \\ \angle x + 54°=180° \\ \angle x =180°- 54° \\  \angle x =126°
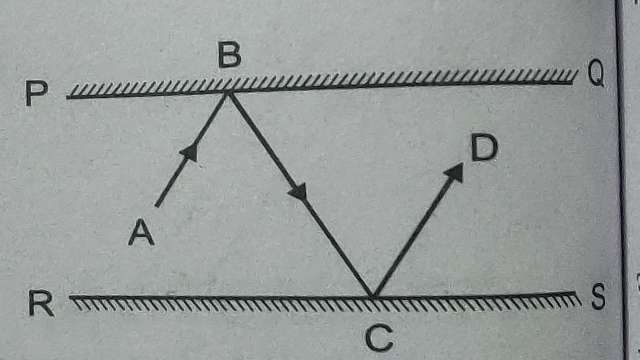
Example-10.चित्र में PQ और RS दो दर्पण है जो परस्पर समान्तर हैं।एक आपतित किरण AB दर्पण PQ के बिन्दु B से परावर्तित होकर पथ BC पर चलकर दर्पण RS के बिन्दु C से पुनः परावर्तित होकर पथ CD के अनुदिश चलती है तो सिद्ध कीजिए है।

Solution-दिया है (Given): किरण AB दर्पण PQ के बिन्दु B से परावर्तित होकर पथ BC पर चलकर दर्पण RS के बिन्दु C से पुनः परावर्तित होकर पथ CD के अनुदिश चलती है।
सिद्ध करना है (To Prove):AB \parallel CD
रचना (Construction): BE \perp  PQ \text { व } CF \perp  RS खींचा।
उपपत्ति (Proof):AB आपतित व BC परावर्तित किरण हैं अतः
\angle ABE =\angle CBE (आपतन कोण व परावर्तन कोण बराबर होते है)……..(1)
इसी प्रकार BC आपतित व CD परावर्तित किरण हैं अतः
\angle BCF =\angle DCF (आपतन कोण व परावर्तन कोण बराबर होते हैं)………..(2)
PQ \parallel RS (दिया है)

BE \perp  PQ \text { व } CF \perp  RS( रचना से )
अतः BE \parallel CF \\  \angle EBC =\angle BCF (एकान्तर कोण)………(3)
समीकरण (1),(2) व (3) से-

\angle ABC =\angle BCD
ये एकान्तर कोण हैं तथा समान हैं और तिर्यक रेखा BC इनको काटती है।
अतः AB \parallel CD
Example-11.चित्र में यदि PQ \parallel RS,\angle MXQ=135° \text { और } \angle MYR=40° है,तो \angle XMY ज्ञात कीजिए।

Solution–UT \parallel PQ  \parallel RS रेखा खींची।
\angle QXM + \angle XMT =180°(अन्त: कोणों का योग)

\Rightarrow  \angle QXM + \angle XMT =180° \\ \Rightarrow 135°+ \angle XMT =180° \\ \Rightarrow \angle XMT =180°-135° \\  \Rightarrow  \angle XMT =45° \\  RT  \parallel RS \\ \text { अतः }  \angle RYM = \angle TMY (एकान्तर कोण)

\angle TMY =40° \\  \angle XMY = \angle XMT + \angle TMY \\  \Rightarrow  \angle XMY =45°+40° \\ \Rightarrow \angle XMY =85°
उपर्युक्त उदाहरणों के द्वारा कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9), रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9) को समझ सकते हैं।

6.कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9 Problems), रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9 Problems)-

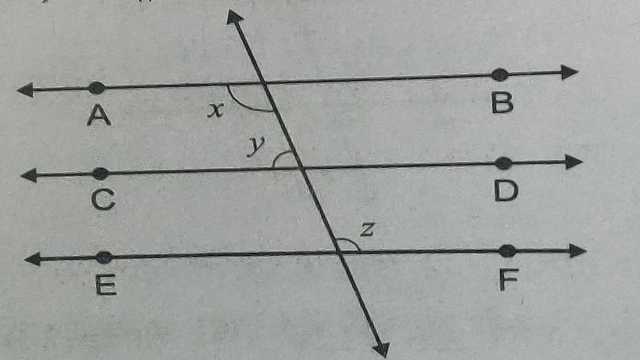
(1.)चित्र में रेखाएं AB,CD तथा EF परस्पर समान्तर हैं तो \angle x, \angle y , \angle z \text { और } \angle p ज्ञात कीजिए।

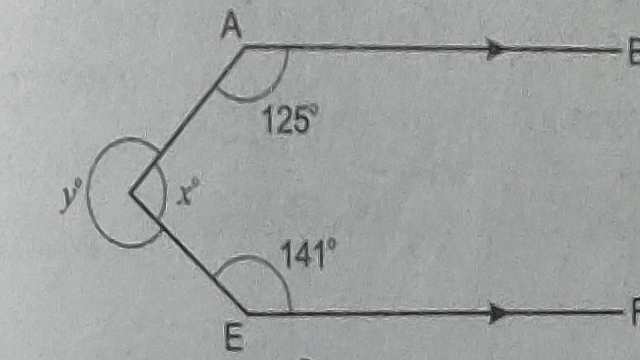
(2.)चित्र में AB \parallel EF है। \angle x \text { एवं } \angle y ज्ञात कीजिए।

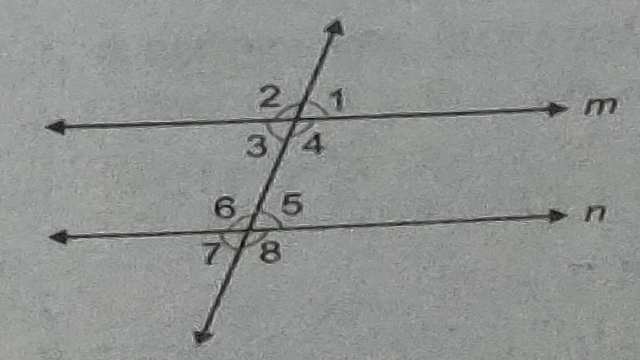
(3.)चित्र में l \parallel m \text { तो  } \angle 1 के तुल्य कोणों को बताइए।

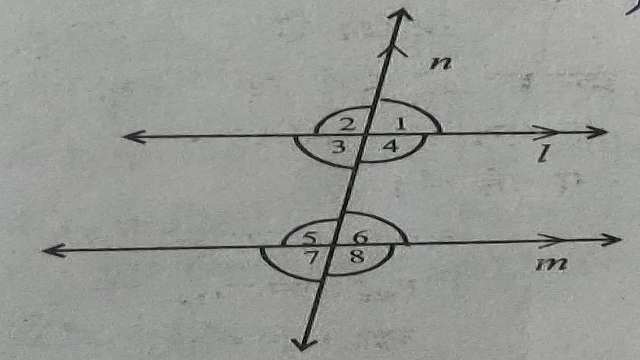
(4.)चित्र में \angle 1=60° \text { और } \angle 6=120° है।तो दर्शाइए कि m और n समान्तर है।

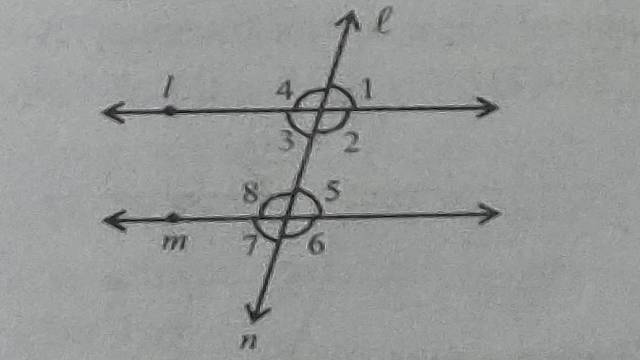
(5.) चित्र में रेखाएं l,m और n तिर्यक रेखा उन्हें काटती है।यदि \angle 1=55° हो तो शेष कोण ज्ञात कीजिए।

उत्तर (Answers): (1) \angle x=58° , \angle y=122° , \angle z=58° , \angle x=58° , \angle p=122° \\ (2) \angle x=94° , \angle y=266°  \\ (3) \angle 3 , \angle 5, \angle 7 \\ (4) 90° \\ (5) \angle 3=55° , \angle 6=55° , \angle 4=125° , \angle 2=125° , \angle 5=125° , \angle 8=125°, \angle 7=55°
उपर्युक्त सवालों को हल करके कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9), रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9) को ठीक से समझा जा सकता है।

7.लाइन और एंगल क्या है? (What is line and angle?)-

लाइन्स एंड एंगल्स – परिभाषाएँ, गुण, प्रकार, अभ्यास प्रश्न।यूक्लिड द्वारा चौड़ाई के कम लंबाई के रूप में माना जाता है, लाइनें यूक्लिडियन ज्यामिति का आधार बनती हैं। जब दो किरणें (एक सीधी रेखा का हिस्सा) एक ही तल में एक-दूसरे को काटती हैं, तो वे एक कोण बनाती हैं।प्रतिच्छेद के बिंदु को एक शीर्ष कहा जाता है।

8.कक्षा 9 में कोण क्या है? (What is an angle Class 9?)-

कोण: एक कोण तब बनता है जब दो किरणें एक ही समापन बिंदु से उत्पन्न होती हैं।
उदाहरणों के साथ गणित में कोण के प्रकार
(i)शून्य कोण (Zero Angle)। एक शून्य कोण (0°) एक कोण बनता है जब कोण के दोनों भुजाएं एक ही स्थिति में होते हैं।
(ii)न्यून कोण (Acute Angle)।एक न्यून कोण एक कोण है जो 0° से अधिक है लेकिन 90° से कम है।
(iii)समकोण (Right Angle)-90 डिग्री कोण।
(iv) ऑब्सट्यूज एंगल (Obtuse Angle): एक ऑब्सट्यूज एंगल एक एंगल है जो 90° से अधिक और 180° से कम है।अधिक कोण: 90°<z<180°
(iv) सरल कोण (Straight Angle): एक सरल कोण एक कोण होता है जो 180° के बराबर होता है।
(v)वृहत कोण,पुनर्युक्त कोण (Reflex Angle):वह कोण जिसका परिणाम 180° से अधिक परन्तु 360° से कम हो। आकृति में एक वृहत कोण है।
(vi)पूर्ण कोण (Complete Angle)-वह कोण जो एक बिन्दु पर बनता है तथा जिसका मान 180° होता।

9.रेखाएँ और कोण कितने प्रकार के होते हैं? (How many types of lines and angles are there?)-

सरल रेखा: एक सीधी रेखा में न तो शुरुआत होती है और न ही अंत बिंदु और अनंत लंबाई होती है।न्यून कोण: वह कोण जो 0° और 90° के बीच होता है,एक न्यून कोण होता है, जो ऊपर दिए गए चित्र में दर्शाया है।ऑब्सट्यूज एंगल: 90 डिग्री और 180 डिग्री के बीच का कोण एक ऑब्सट्यूड एंगल है, जैसा कि ऊपर दिखाया गया है।

10.गणित में रेखाएँ क्या हैं? (What are lines in math?)-

ज्यामिति में, एक रेखा को सीधी एक आयामी आकृति के रूप में परिभाषित किया जा सकता है जिसकी कोई मोटाई नहीं है और दोनों दिशाओं में अंतहीन रूप से फैली हुई है। इसे अक्सर किसी भी दो बिंदुओं के बीच की सबसे छोटी दूरी के रूप में वर्णित किया जाता है।यहां, P और Q लाइन पर स्थित बिंदु हैं।
उपर्युक्त प्रश्नों के उत्तर,उदाहरणों और सवालों को हल करने पर कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9), रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9) को भली-भांति समझा जा सकता है।

Also Read This Article:-Congruence of Triangles

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here