Angles of a Triangle
1.त्रिभुज के कोण (Angles of a Triangle),त्रिभुज के कोणों का योग (Sum of Angles of a Triangle):
त्रिभुज के कोण (Angles of a Triangle): त्रिभुज में तीन प्रकार के कोण होते हैं-समकोण,न्यूनकोण तथा अधिककोण।
समकोण (Right Angle):जिस कोण का मान 90° हो उसे समकोण कहते हैं।
न्यूनकोण (Acute Angle):जिस कोण का मान 90° या समकोण से कम होता है उसे न्यूनकोण कहते हैं।जैसे- 75°,60°,35° इत्यादि।
अधिककोण (Obtuse Angle):वे कोण जिनका मान 90° अर्थात् समकोण से अधिक होता है तथा 180° से कम होता है उसे अधिक कोण कहते हैं जैसे- 135°,160°,105° इत्यादि।
कोणों के आधार पर त्रिभुजों का वर्गीकरण या कोणों के आधार पर त्रिभुजों के प्रकार (Classification of Triangles by Angeles Or Types of Triangles by Angeles):
(1.)न्यून कोण त्रिभुज (Acute Angle Triangle):
जिस त्रिभुज का प्रत्येक कोण न्यून कोण हो उसे न्यून कोण त्रिभुज कहते हैं।
(2.)समकोण त्रिभुज (Right Angled Triangle):
जिस त्रिभुज का एक कोण 90° के बराबर हो उसे समकोण त्रिभुज कहते हैं।
(3.)अधिककोण त्रिभुज (Obtuse Angled Triangle):
जिस त्रिभुज में कोई कोण 90° से अधिक हो उसे अधिककोण त्रिभुज कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Mid Point Theorem
2.त्रिभुज के कोण के उदाहरण (Angles of a Triangle Examples),त्रिभुज के कोणों का योग के उदाहरण (Sum of Angles of a Triangle Examples):
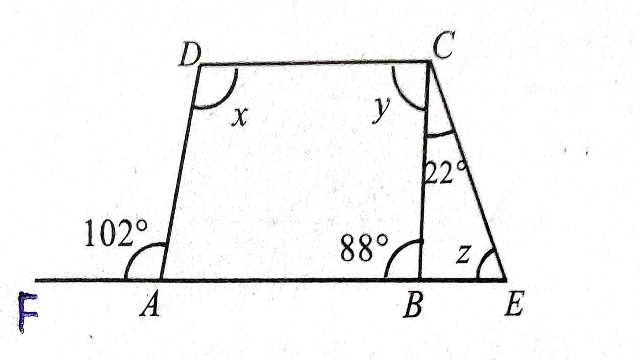
Example-1.चित्र में AB \parallel CD हो तो दिए गए कोणों से \angle x, \angle y तथा \angle z ज्ञात कीजिए।
Solution– AB \parallel CD अतः
\angle ADC= \angle DAF (एकान्तर कोण)
\angle x=102^{\circ}
\triangle BCE में
\angle ABC= \angle BCE+\angle BEC(बहिष्कोण=अन्तराभिमुख कोणों का योग)
\Rightarrow 88^{\circ}=22^{\circ}+\angle z \\ \Rightarrow \angle z=88^{\circ}-22^{\circ} \\ \Rightarrow \angle z= 66^{\circ} \\ \angle CBE+ \angle BEC+ \angle BCE=180^{\circ} \\ \Rightarrow \angle CBE+66^{\circ}+ 22^{\circ} =180^{\circ} \\ \Rightarrow \angle CBE+88^{\circ}=180^{\circ} \\ \Rightarrow \angle CBE=180^{\circ}-88^{\circ} \\ \Rightarrow \angle CBE=92^{\circ} \\ \angle BCD=\angle CBE (एकान्तर कोण)
\angle y=92^{\circ}
अतः \angle x=102^{\circ},\angle y=92^{\circ} ,\angle z= 66^{\circ}
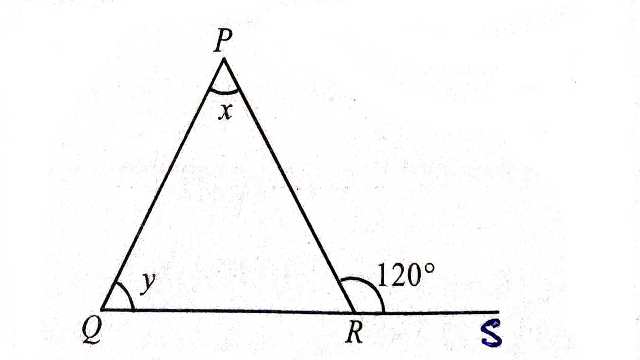
Example-2.दिए गए चित्र से \angle x तथा \angle y के माप ज्ञात कीजिए जहां \angle x - \angle y =10^{\circ} है।
Solution–\triangle PQR में
\angle x +\angle y =120^{\circ} (बहिष्कोण=अन्तराभिमुख कोणों का योग)…..(1)
\angle x - \angle y =10^{\circ} \cdots(2) \\ ..........................\text{ जोड़ने पर } \\ 2 \angle x=130^{\circ} \\ \Rightarrow \angle x=\frac{130^{\circ}}{2} \\ \Rightarrow \angle x=65^{\circ}
\angle x का मान समीकरण (1) में रखने पर-
65^{\circ} +\angle y =120^{\circ} \\ \Rightarrow \angle y =120^{\circ}-65^{\circ} \\ \Rightarrow \angle y =55^{\circ} \\ \angle x=65^{\circ},\angle y =55^{\circ}
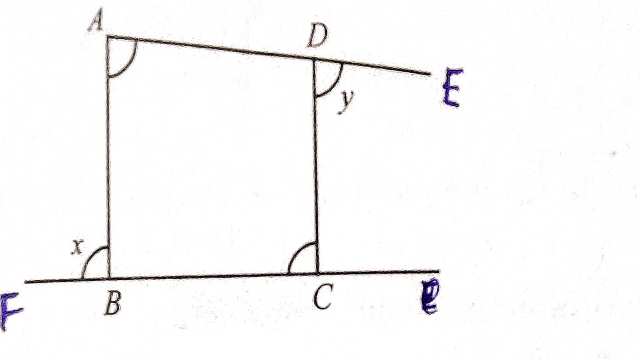
Example-3.दिए गए चित्र से सिद्ध कीजिए कि \angle x +\angle y =\angle A +\angle C
Solution–\triangle ABC में
\angle ABF=\angle BAC +\angle BCA \cdots(1)
(बहिष्कोण=अन्तराभिमुख कोणों का योग)
\triangle ACD में
\angle CDE=\angle DAC +\angle DCA \cdots(2)
(बहिष्कोण=अन्तराभिमुख कोणों का योग)
(1) व (2) को जोड़ने पर-
\angle ABF+\angle CDE=\angle BAC +\angle BCA+\angle DAC +\angle DCA \\ \Rightarrow \angle x +\angle y=\left( \angle BAC +\angle DAC \right)+\left( \angle BCA+\angle DCA \right) \\ \Rightarrow \angle x +\angle y=\angle A +\angle C
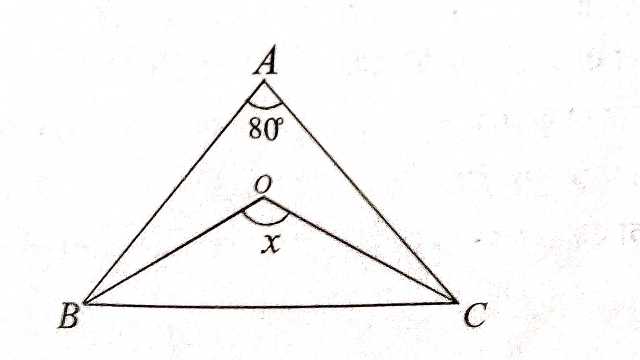
Example-4.दिए गए चित्र से \angle x ज्ञात कीजिए।यहां रेखाएं BO एवं CO क्रमशः \angle B एवं \angle C के समद्विभाजक हैं।
Solution– \triangle ABC में
\angle ABC +\angle ACB+\angle A=180^{\circ} \\ \Rightarrow \angle ABC+\angle ACB+80^{\circ}=180^{\circ} \\ \Rightarrow \angle ABC+\angle ACB=100^{\circ} \\ \Rightarrow \frac{1}{2} \angle ABC+ \frac{1}{2} \angle ACB= 50^{\circ} \cdots(1) \\ \angle ABO=\angle OBC तथा \angle ACO=\angle OCB \cdots(2)
(BO तथा CO समद्विभाजक हैं)
समीकरण (1) व (2) से –
\Rightarrow \angle OBC+\angle OCB=50^{\circ} \cdots(3) \\ \left( \frac{1}{2} \angle ABC=\angle OBC,\frac{1}{2} \angle ACB=\angle OCB \right)
समीकरण (3) के दोनों पक्षों में \angle BOC जोड़ने पर-
\angle BOC +\angle DBC+\angle OCB=\angle BOC+50^{\circ} \\ \Rightarrow 180^{\circ}=\angle BOC+50^{\circ} (त्रिभुज के तीनों कोणों का योग)
\Rightarrow \angle BOC=180^{\circ}-50^{\circ} \\ \Rightarrow \angle BOC=130^{\circ} \\ \Rightarrow \angle x=130^{\circ}
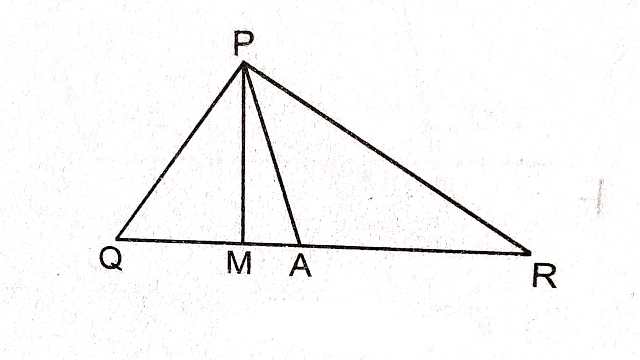
Example-5.चित्र में \angle Q>\angle R ,PA कोण QPR का समद्विभाजक है तथा PM \perp QR है।सिद्ध कीजिए \angle APM=\frac{1}{2}\left ( \angle Q-\angle R \right )
Solution–\triangle APM में PM \perp QR \\ \angle PAM+\angle APM=90^{\circ} \cdots(1)
\triangle APR में
\angle PAM= \angle APR+ \angle R
(बहिष्कोण=अन्तराभिमुख कोणों का योग)
\angle PAM-\angle APR= \angle R \cdots(2)
\triangle PQM में
\angle AMP=\angle Q+\angle QPM
(बहिष्कोग=अन्तराभिमुख कोणों का योग)
\Rightarrow 90^{\circ}=\angle Q+\angle QPM \\ \Rightarrow \angle Q=90^{\circ}-\angle QPM \cdots(3)
समीकरण (3) में से (2) घटाने पर-\left (\because \angle Q>\angle R \right )
\angle Q-\angle R=90^{\circ}-\angle QPM-\left ( \angle PAM-\angle APR \right ) \\ \Rightarrow \angle Q-\angle R=90^{\circ}-\angle QPM-\angle PAM+\angle APR \\ \Rightarrow \angle Q-\angle R=90^{\circ}-\angle QPM-\left ( 90^{\circ}-\angle APM\right )+\angle APR[(1) से ]
\Rightarrow \angle Q-\angle R=90^{\circ}-\angle QPM-90^{\circ}+\angle APM+\angle APR \\ \Rightarrow \angle Q-\angle R=-\angle QPM+\angle APM+\angle APR \\ \Rightarrow \angle Q-\angle R=-\angle QPM+\angle APM+\angle APQ [\because \angle APR=\angle APQ ] \\ \Rightarrow \angle Q-\angle R=\angle APQ-\angle QPM +\angle APM \\ \Rightarrow \angle Q-\angle R=\angle APM+\angle APM \\ \Rightarrow \angle Q-\angle R=2 \angle APM \\ \Rightarrow \angle APM=\frac{1}{2}\left ( \angle Q-\angle R \right )
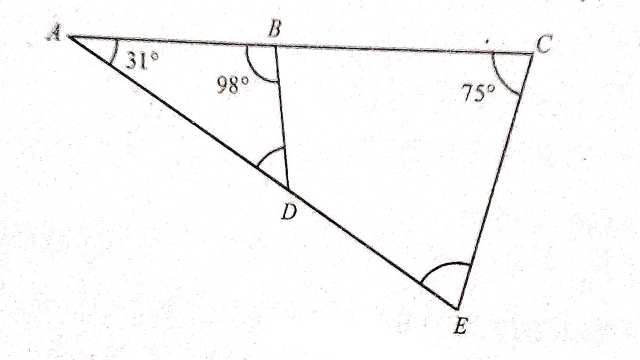
Example-6.नीचे दिए गए चित्र में \angle CED तथा \angle BDE ज्ञात कीजिए।
Solution–\triangle ABD में
\angle A+\angle ABD +\angle BDA=180^{\circ} \\ \Rightarrow 31^{\circ}+98^{\circ}+\angle BDA=180^{\circ} \\ \Rightarrow 129^{\circ}+\angle BDA=180^{\circ} \\ \Rightarrow \angle BDA=180^{\circ}-129^{\circ} \\ \Rightarrow \angle BDA=51^{\circ} \\ \angle BDA+\angle BDE=180^{\circ} (रैखिक कोण युग्म)
51^{\circ}+\angle BDE=180^{\circ} \\ \Rightarrow \angle BDE=180^{\circ} -51^{\circ} \\ \Rightarrow \angle BDE=129^{\circ}
\triangle ACE में
\angle A+\angle ACE+\angle CED=180^{\circ} \\ \Rightarrow 31^{\circ}+75^{\circ}+\angle CED=180^{\circ} \\ \Rightarrow 106^{\circ}+\angle CED=180^{\circ} \\ \Rightarrow \angle CED=180^{\circ}-106^{\circ} \\ \Rightarrow \angle CED=74^{\circ} \\ \angle CED=74^{\circ},\angle BDE=129^{\circ}
Example-7.चित्र में \triangle ABC की भुजा BC को बिन्दु D तक बढ़ाया गया है।यदि \angle A=55^{\circ} और \angle B=60^{\circ} हो तो का माप है:
Solution–\triangle ACD में
\angle ACD=\angle A+\angle B
(बहिष्कोण=अन्तराभिमुख कोणों का योग)
\angle ACD=55^{\circ}+60^{\circ} \\ \Rightarrow \angle ACD=115^{\circ}
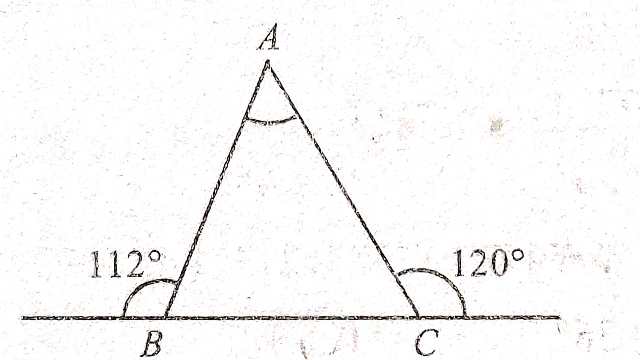
Example-8.चित्र में \angle A का माप बताइए।
Solution–112^{\circ}+\angle ABC=180^{\circ}(रैखिक कोण युग्म से)
\Rightarrow \angle ABC=180^{\circ}-112^{\circ} \\ \Rightarrow \angle ABC=68^{\circ} \\ 120^{\circ}+\angle ACB=180^{\circ} (रैखिक कोण युग्म से)
\Rightarrow \angle ACB=180^{\circ}-120^{\circ} \\ \Rightarrow \angle ACB=60^{\circ}
\triangle ABC में
\angle A+\angle ABC +\angle ACB=180^{\circ} (त्रिभुज के तीनों अन्त: कोणों का योग)
\Rightarrow \angle A+68^{\circ} +60^{\circ}=180^{\circ} \\ \Rightarrow \angle A+128^{\circ}=180^{\circ} \\ \Rightarrow \angle A=180^{\circ}-128^{\circ} \\ \Rightarrow \angle A=52^{\circ}
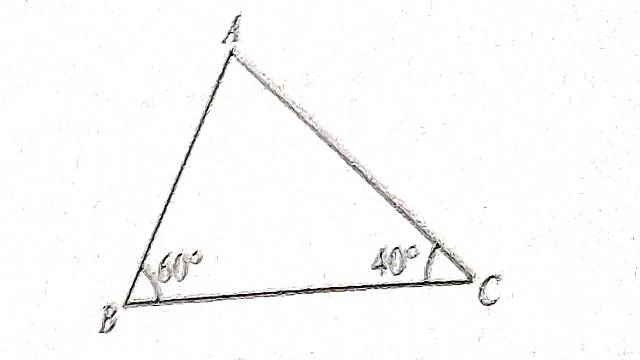
Example-9.चित्र में \angle B=60^{\circ} और \angle C=40^{\circ} है। \angle A का माप बताइए।
Solution–\triangle ABC में
\angle A+\angle B+\angle C=180^{\circ}
(त्रिभुज के तीनों अन्त: कोणों का योग)
\Rightarrow \angle A+60^{\circ}+40^{\circ}=180^{\circ} \\ \Rightarrow \angle A+100^{\circ}=180^{\circ} \\ \Rightarrow \angle A=180^{\circ}-100^{\circ} \\ \Rightarrow \angle A=80^{\circ}
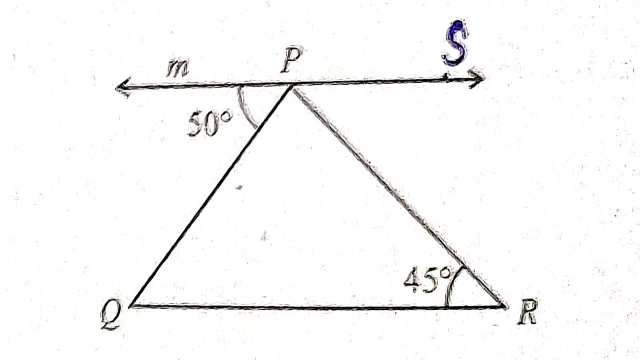
Example-10.चित्र में m \parallel QR तो \angle QPR का माप बताइए।
Solution–m \parallel QR \\ \angle SPR=\angle PRQ (एकान्तर कोण)
\Rightarrow \angle SPR=45^{\circ} \\ 50^{\circ}+\angle QPR+\angle SPR=180^{\circ} (रैखिक कोण युग्म से)
\Rightarrow 50^{\circ}+\angle QPR+45^{\circ}=180^{\circ} \\ \Rightarrow \angle QPR+95^{\circ}=180^{\circ} \\ \Rightarrow \angle QPR=180^{\circ}-95^{\circ} \\ \Rightarrow \angle QPR=85^{\circ}
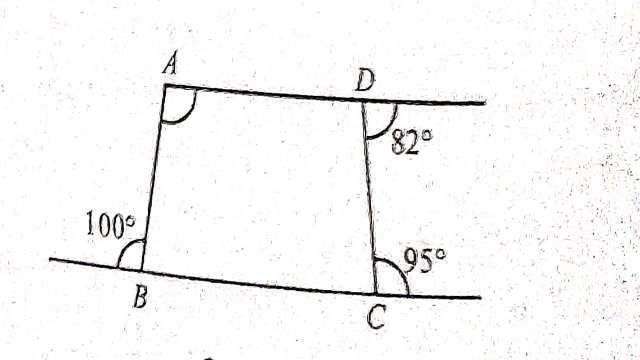
Example-11.चित्र में \angle A का मान बताइए।
Solution–\angle ABC+100^{\circ}=180^{\circ}(रैखिक कोण युग्म से)
\Rightarrow \angle ABC=180^{\circ}-100^{\circ} \\ \Rightarrow \angle ABC=80^{\circ} \\ \angle BCD+95^{\circ}=180^{\circ} (रैखिक कोण युग्म से)
\angle BCD=180^{\circ}-95^{\circ} \\ \Rightarrow \angle BCD=85^{\circ} \\ \angle ADC+82^{\circ}=180^{\circ} (रैखिक कोण युग्म से)
\Rightarrow \angle ADC+180^{\circ}-82^{\circ} \\ \Rightarrow \angle ADC=98^{\circ}
चतुर्भुज ABCD में
\angle A+\angle ABC +\angle BCD+\angle ADC=360^{\circ} \\ \Rightarrow \angle A+80^{\circ} +85^{\circ}+98^{\circ}=360^{\circ} \\ \Rightarrow \angle A+263^{\circ}=360^{\circ} \\ \Rightarrow \angle A=97^{\circ}
उपर्युक्त उदाहरणों के द्वारा त्रिभुज के कोण (Angles of a Triangle),त्रिभुज के कोणों का योग (Sum of Angles of a Triangle) को समझ सकते हैं।
3.त्रिभुज के कोण की समस्याएं (Angles of a Triangle Problems),त्रिभुज के कोणों का योग (Sum of Angles of a Triangle Problems):
(1.)चित्र में यदि BE \perp AC ,\angle EBC=30^{\circ} और \angle FAC=20^{\circ} है,तो \angle x और \angle y के मान ज्ञात कीजिए।
(2.)यदि किसी त्रिभुज ABC के कोण B तथा C के समद्विभाजक बिन्दु O पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए कि \angle BOC=90^{\circ}+ \frac{1}{2} \angle A
उत्तर (Answer):\angle x=60^{\circ} ,\angle y=80^{\circ}
उपर्युक्त सवालों को हल करने पर त्रिभुज के कोण (Angles of a Triangle),त्रिभुज के कोणों का योग (Sum of Angles of a Triangle) को ठीक से समझ सकते हैं।
Also Read This Article:-What Are The Angles Of A Triangle?
4.त्रिभुज के कोण (Angles of a Triangle),त्रिभुज के कोणों का योग (Sum of Angles of a Triangle) के बारे में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिभुज कितने प्रकार के होते हैं? (What are the 3 Types of Triangles?):
उत्तर-भुजाओं के आधार पर त्रिभुजों का वर्गीकरण (Classification of Triangles by Sides):
(1.)विषमबाहु त्रिभुज (Scalene Triangle):
जिस त्रिभुज की तीनों भुजाएं अलग-अलग माप की हो उसे विषमबाहु त्रिभुज कहते हैं।
(2.)समद्विबाहु त्रिभुज (Isosceles Triangle):
यदि किसी त्रिभुज की भुजाएं समान माप की हों तो उसे समद्विबाहु त्रिभुज कहा जाता है।
(3.)समबाहु त्रिभुज (Equilateral Triangle):
जिस त्रिभुज में सभी भुजाएं समान माप की हो,उसे समबाहु त्रिभुज कहते हैं।
कोणों के आधार पर त्रिभुजों का वर्गीकरण (Classification of Triangles by Angeles):
(1.)न्यून कोण त्रिभुज (Acute Angle Triangle):
जिस त्रिभुज का प्रत्येक कोण न्यून कोण हो उसे न्यून कोण त्रिभुज कहते हैं।
(2.)समकोण त्रिभुज (Right Angled Triangle):
जिस त्रिभुज का एक कोण 90° के बराबर हो उसे समकोण त्रिभुज कहते हैं।
(3.)अधिककोण त्रिभुज (Obtuse Angled Triangle):
जिस त्रिभुज में कोई कोण 90° से अधिक हो उसे अधिककोण त्रिभुज कहते हैं।
प्रश्न:2. मैं त्रिभुज में कोण का माप कैसे ज्ञात करूं? (How do I find the Measure of an Angle in a Triangle?):
उत्तर-एक त्रिभुज के आंतरिक कोण हमेशा 180 डिग्री तक जोड़ते हैं और यह दिया गया था कि त्रिभुज समकोण था, जिसका अर्थ है कि कोणों में से एक 90 डिग्री मापता है।
एक त्रिभुज के तीनों आंतरिक कोणों का योग 180 डिग्री के बराबर होता है।A+ B+ C= 180º।
एक त्रिभुज की लंबाई और आंतरिक कोण सीधे संबंधित हैं, इसलिए यह समझ में आता है कि एक समबाहु त्रिभुज में तीन भुजाएं तथा तीनों कोण बराबर होते हैं अर्थात् प्रत्येक कोण 60° का होता है।
प्रश्न:3.आप ज्यामिति में त्रिभुज कैसे करते हैं? (How do you do Triangles in Geometry?):
उत्तर-यदि समतल में कोई असंरेख बिन्दु लें और स्केल द्वारा दो-दो बिन्दुओं को लेकर रेखाखण्ड खींचे तो कुल तीन रेखाखण्ड खींचे जा सकते हैं।इस प्रकार तीन रेखाखण्डों से घिरी हुई आकृति को त्रिभुज कहते हैं।
प्रश्न:4.त्रिभुज के कोणों के सूत्र (Angles of a Triangle Formula):
उत्तर-त्रिभुज के तीनों अन्त: कोणों का योग 180° होता है। अर्थात् यदि त्रिभुज के तीन कोण क्रमशःA,B,C हो तो-
A+B+C=180°
त्रिभुज के तीनों बहिष्कोणों का योग 360° होता है।
त्रिभुज का बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है।
प्रश्न:5.त्रिभुज और कोण प्रश्नोत्तरी (Triangles and Angles Quiz):
उत्तर-एक त्रिभुज में तीन शीर्ष तथा तीन भुजाएं होती है। प्रत्येक त्रिभुज में कम से कम दो कोण अवश्य न्यूनकोण होते हैं।किसी त्रिभुज की भुजाओं को क्रमानुसार आगे बढ़ाया जाए तो बढ़ी हुई भुजा और अन्य संलग्न भुजा के बीच बने कोण को त्रिभुज का बहिष्कोण कहते हैं।
प्रश्न:6.त्रिभुज का कोण कैसे ज्ञात करें? (How to Find the Angle of a Triangle?):
उत्तर-त्रिभुज के तीनों कोणों का योगफल दो समकोण के बराबर होता है।अर्थात् यदि त्रिभुज के तीन कोण A,B,C हों तो A+B+C=180°
यदि किसी त्रिभुज की एक भुजा को आगे बढ़ा दिया जाए तो इस प्रकार बना बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है।
इन दोनों के आधार पर किसी त्रिभुज का कोण ज्ञात किया जा सकता है।
कई बार रैखिक कोण अभिग्रहीत को भी त्रिभुज के कोण ज्ञात करने के प्रयोग में लेते हैं।
प्रश्न:7.विषमबाहु त्रिकोण (Scalene Triangle):
उत्तर-विषमबाहु त्रिभुज (Scalene Triangle):
जिस त्रिभुज की तीनों भुजाएं अलग-अलग माप की हो उसे विषमबाहु त्रिभुज कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुज के कोण (Angles of a Triangle),त्रिभुज के कोणों का योग (Sum of Angles of a Triangle) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
