Mid Point Theorem
1.मध्य बिन्दु प्रमेय (Mid Point Theorem),मध्य बिन्दु प्रमेय कक्षा 9 (Mid Point Theorem Class 9)-
मध्य बिन्दु प्रमेय (Mid Point Theorem) में कहा गया है कि त्रिभुज की दो भुजाओं के मध्य बिन्दु से मिलाने वाला रेखाखण्ड त्रिभुज की तीसरी भुजा के समान्तर होता है और यह तीसरी भुजा की लम्बाई का आधा होता है।
अब तक त्रिभुज और चतुर्भुज के अनेक गुणों के बारे में अध्ययन किया है।अब त्रिभुज की भुजाओं के मध्य बिन्दु सम्बन्धी एक अन्य गुण पर विचार करते हैं।
प्रमेय (Theorem):1.मध्य बिन्दु प्रमेय कथन (Mid Point Theorem State)-किसी त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर एवं उसका आधा होता है।
मध्य बिन्दु प्रमेय प्रमाण (Mid Point Theorem Proof),त्रिभुज मध्यबिंदु प्रमेय प्रमाण (Triangle Midpoint Theorem Proof):
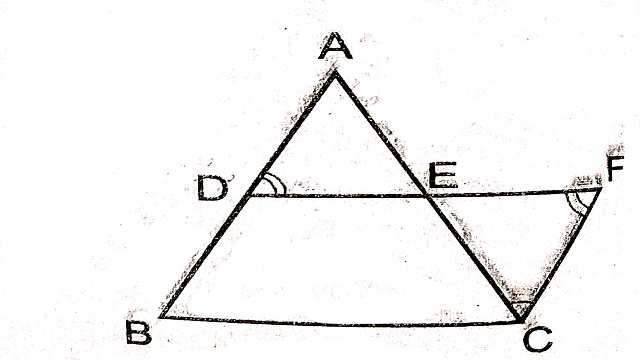
दिया है (Given): त्रिभुज ABC में बिन्दु D और E क्रमशः भुजाओं AB और AC के मध्य बिन्दु हैं।
सिद्ध करना है (To Prove):(1)DE \parallel BC \quad (2) DE=\frac{1}{2}BC
रचना (Construction):DE को F तक बढ़ाया जहां EF=DE ,C को F से मिलाया।
उपपत्ति (Proof): \triangle ADE और \triangle CFE में
AE=CE (दिया है)
\angle AED=\angle CEF (शीर्षाभिमुख कोण)
DE=EF (रचना से)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ADE \cong \triangle CFE
अतः सर्वांगसम त्रिभुजों की संगत भुजाएं और कोण समान होंगे
AD=CF
\angle EAD=\angle ECF.......(1)
तिर्यक रेखा AC रेखाओं AB और CF को प्रतिच्छेद करती है और एकान्तर कोण \angle EAD तथा \angle ECF बराबर हैं। अतः
AD \parallel CF और BD \parallel CF......(2)
परन्तु दिया है कि AD=BD……(3)
(1) और (3) से-
BD=CF
अर्थात् BD=CF और BD \parallel CF
अतः BCFD एक समान्तर चतुर्भुज है।
\therefore DFएवं BC भी समान और समान्तर है।
या DE \parallel BC
\therefore DE=\frac{1}{2}DF (रचना से)
अतः DE=\frac{1}{2}BC
प्रमेय (Theorem):2.[मध्य बिन्दु प्रमेय का विलोम (Converse of Mid Point Theorem), मध्य बिन्दु प्रमेय विलोम (Mid-Point Theorem Converse):
त्रिभुज की एक भुजा के मध्य बिन्दु से,एक अन्य भुजा के समान्तर खींची गई रेखा, तीसरी भुजा को समद्विभाजित करती है।
दिया है (Given):चित्र में \triangle ABC की भुजा AB का मध्य बिन्दु D है DE \parallel BC और AC को E पर काटती है।
सिद्ध करना है (To Prove):AE=EC
रचना (Construction):BD के समान्तर रेखा CF खींची जो DE (बढ़ी हुई) को F पर प्रतिच्छेद करती है।
उपपत्ति (Proof):BC \parallel CF (दिया है)
BD \parallel CF (रचना से)
अतः BCFD एक समान्तर चतुर्भुज है।
BD=CF …….(1)
परन्तु BD=AD (दिया है)
\therefore AD=CF
अब \triangle ADE और \triangle CFE में
\angle ADE=\angle CFE (एकान्तर कोण)
AD=CF [(1) से]
\angle DAE=\angle ECF (एकान्तर कोण)
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Congruence Property)
\triangle ADE \cong \triangle CFE
अतः AE=CE
अन्त:खण्ड (Intercept):
यदि एक समतल में दो रेखाएं l_{1} और l_{2} हों और यदि एक तीसरी रेखा l_{3} उन्हें भिन्न-भिन्न बिन्दुओं A और B पर प्रतिच्छेद करती हो तो रेखाखण्ड AB दी गई रेखाओं l_{1} और l_{2} द्वारा तीसरी रेखा l_{3} पर बनाया गया अन्त:खण्ड कहलाता है।
प्रमेय (Theorem):3 यदि तीन या अधिक समान्तर रेखाएं हों और उनके द्वारा एक तिर्यक रेखा पर बनाए गए अन्त:खण्ड बराबर हों तो किसी अन्य तिर्यक रेखा पर संगत अन्त:खण्ड भी बराबर होंगे।
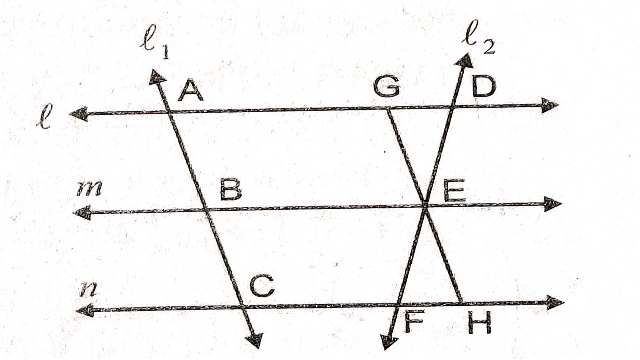
दिया है (Given):चित्र में l,m,n तीन समान्तर रेखाएं हैं और दो तिर्यक रेखाएं l_{1} तथा l_{2} उनको क्रमशः A,B,C और D,E,F बिन्दुओं पर प्रतिच्छेद करती है तथा AB=BC है।
सिद्ध करना है (To Prove):DE=EF
रचना (Construction):तिर्यक रेखा l_{1} के समान्तर रेखा GH खींची जो E से गुजरती है।
उपपत्ति (Proof):l एवं m समान्तर रेखाएं हैं।अतः
AG \parallel BE
एवं AB \parallel GE (रचना से)
\therefore ABEG एक समान्तर चतुर्भुज है।
अतः AB=GE …..(1)
इसी प्रकार BCHE भी एक समान्तर चतुर्भुज है।
अतःBC=EH ……(2)
दिया हुआ है कि AB=BC
अतःGE=EH ……(3)
पुनः l और m समान्तर रेखाएं हैं और तिर्यक रेखा l_{2} उनको प्रतिच्छेद करती है।अतः
\angle GDE=\angle EFH(एकान्तर कोण)…..(4)
अतः \triangle GDE और \triangle HFE में
\angle GDE=\angle EFH[(4) से]
GE=EH [(3) से]
\angle GED=\angle FEH (शीर्षाभिमुख कोण)
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Congruence Property)
\triangle GDE \cong \triangle HFE
अतः सर्वांगसम त्रिभुजों की संगत भुजाएं समान होंगी
अर्थात् DE=EF
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Properties of Parallelograms Diagonals
2.मध्य बिन्दु प्रमेय उदाहरण (Mid Point Theorem Examples)-
Example-1.एक त्रिभुज \triangle ABC के शीर्षों A,B और C से होकर क्रमशः भुजाओं BC,CA और AB के समान्तर रेखाएं RQ,PR और QP चित्र में दर्शाए अनुसार खींची गई है।दर्शाइए कि BC=\frac{1}{2} QR है।
Solution-दिया है (Given): \triangle ABC के शीर्षो A,B और C से होकर भुजाओं BC,CA और AB के समान्तर रेखाएं RQ,PR और QP खींची गई हैं अर्थात् BC \parallel QR ,CA \parallel PR तथा AB \parallel QP
सिद्ध करना है (To Prove):BC=\frac{1}{2} QR
उपपत्ति (Proof): चतुर्भुज BCAR में
BC \parallel QR(दिया है)
BR \parallel CA(दिया है)
अतः BCAR समान्तर चतुर्भुज है।फलत:
BC=AR (स.च. की सम्मुख भुजाएं समान होती है) ….(1)
इसी प्रकार चतुर्भुज ABCQ में
BC \parallel AQ (दिया है)
AB \parallel CQ (दिया है)
अतः ABCQ समान्तर चतुर्भुज है।फलत:
BC=AQ (स.च. की सम्मुख भुजाएं समान होती है) ….(2)
(1) व (2) से-
AR=AQ
अतः BC=\frac{1}{2} QR
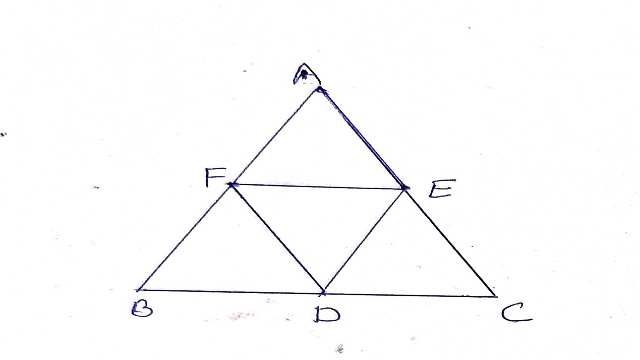
Example-2.D,E और F क्रमशः एक समबाहु \triangle ABC की भुजाओं BC,CA और AB के मध्य बिन्दु है।दर्शाइए कि \triangle DEF भी एक समबाहु त्रिभुज है।
Solution– दिया है (Given):\triangle ABC एक समबाहु त्रिभुज है अर्थात् AB=BC=CA
सिद्ध करना है (To Prove): \triangle DEF समबाहु त्रिभुज है अर्थात् DE=EF=FD
उपपत्ति (Proof):D व E मध्य बिन्दु है
अतः DE=\frac{1}{2} AB (मध्य बिन्दु प्रमेय से) …..(1)
इसी प्रकार E व F मध्य बिन्दु है
अतः EF=\frac{1}{2} BC (मध्य बिन्दु प्रमेय से) …….(2)
D व F मध्य बिन्दु है अतः
DF=\frac{1}{2} AC (मध्य बिन्दु प्रमेय से) …….(3)
AB=BC=CA (दिया है)
अतः \frac{1}{2} AB=\frac{1}{2} BC=\frac{1}{2} AC....(4)
(1),(2),(3) व (4) से-
DE=EF=DF
अतः \triangle DEF समबाहु त्रिभुज है।
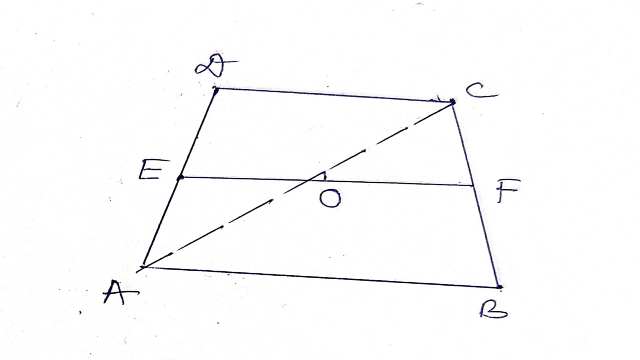
Example-3.E एक समलम्ब चतुर्भुज ABCD की भुजा AD का मध्य बिन्दु है जिसमें AB \parallel DC है।E से होकर AB के समान्तर खींची गई रेखा BC को F पर प्रतिच्छेद करती है।दर्शाइए कि F भुजा BC का मध्य बिन्दु है।
Solution-दिया है (Given):ABCD समलम्ब चतुर्भुज में AB \parallel CD तथा AD का मध्य बिन्दु E है। EF \parallel AB
सिद्ध करना है (To Prove):BF=FC
रचना (Construction):AC को मिलाया जो EF को O पर काटती है।
उपपत्ति (Proof): \triangle ACD में
E,AD का मध्य बिन्दु है तथा EO \parallel CD
[ \because AB \parallel CD तथा EF \parallel AB अतः EF \parallel DC]
AO=OC (मध्य बिन्दु के विलोम से)
\triangle ABC में O,AC का मध्य बिन्दु है
तथा OF \parallel AB (दिया है)
अतः BF=FC (मध्य बिन्दु प्रमेय के विलोम से)
Example-4.चित्र में D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिन्दु है।यदि AB=4.3 सेमी,BC=5.6 सेमी और AC=3.9 सेमी हो तो निम्नलिखित का परिमाप ज्ञात कीजिए।
(1.)\triangle DEF
(2.) चतुर्भुज BDEF
Solution-D व E क्रमशः \triangle ABC की भुजाओं BC व AC के मध्य बिन्दु है
अतः DE=\frac{1}{2} AB(मध्य बिन्दु प्रमेय से)
DE \parallel AB ......(1) \\ DE=\frac{4.3}{2}
DE=2.15
E व F, \triangle ABC की क्रमशः भुजाओं AC व AB के मध्य बिन्दु हैं
अतः EF=\frac{1}{2} BC (मध्य बिन्दु प्रमेय से)
EF \parallel BC (मध्य बिन्दु प्रमेय से) ….(2)
EF=\frac{5.6}{2}
EF=2.8
इसी प्रकार \triangle ABC की क्रमशः भुजाओं AB व BC के मध्य बिन्दु F व D है अतः मध्य बिन्दु प्रमेय से-
DF=\frac{1}{2} BC \\ DF \parallel AC.......(3) \\ DF=\frac{3.9}{2}
DF=1.95
(1.)\triangle DEF का परिमाप
=DE+EF+DF
=2.15+2.8+1.95
=6.90
(2.) DE \parallel AB [(1) से]
अतः BF \parallel DE.....(4)
EF \parallel BC [(2) से]
अतः EF \parallel BD.....(5)
(4) व (5) से-
BDEF एक समान्तर चतुर्भुज है।
अतः समान्तर चतुर्भुज BDEF का परिमाप
=2(EF+DE)
=2(2.8+2.15)
=2×4.95
=9.9सेमी
Example-5.एक चतुर्भुज के विकर्ण परस्पर लम्बवत् हैं। सिद्ध कीजिए कि उसकी भुजाओं के मध्य बिन्दुओं को मिलाने से निर्मित चतुर्भुज एक आयत होता है।
Solution-दिया है (Given): चतुर्भुज ABCD के विकर्ण AC व BD लम्बवत् है।P,Q,R,S क्रमशः भुजाओं AB,BC,CD,DA के मध्य बिन्दु है।
सिद्ध करना है (To Prove):PQRS एक आयत है।
उपपत्ति (Proof): \triangle ABC में P व Q क्रमशः भुजाओं AB व BC के मध्य बिन्दु हैं अतः मध्य बिन्दु प्रमेय से
PQ=\frac{1}{2} AC.....(1) \\ PQ \parallel AC.....(2)
इसी प्रकार \triangle ACD में S व R क्रमशः भुजाओं AD व CD के मध्य बिन्दु हैं अतः मध्य बिन्दु प्रमेय से-
SR=\frac{1}{2} AC.....(3) \\ SR \parallel AC.....(4)
(1) व (3) तथा (2) व (4) से-
PQ=SR , PQ \parallel SR
अतः PQRS एक समान्तर चतुर्भुज है।
इसी प्रकार PS=\frac{1}{2} BD .....(5) \\ PS \parallel BD....(6)
व QR=\frac{1}{2} BD .....(7) \\ QR \parallel BD....(8)
(4) व (6) से-
SV \parallel WO तथा SW \parallel VO
अतः SWOV एक समान्तर चतुर्भुज है।समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
\angle AOV=\angle RSP=90^{\circ}
इसी प्रकार \angle SRQ=\angle DOC=90^{\circ} \\ \angle SPQ=\angle AOB=90^{\circ} \\ \angle PQR=\angle BOC=90^{\circ}
अतः PQRS एक आयत है।
Example-6.सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण को समद्विभाजित करने वाली माध्यिका कर्ण की आधी होती है।
Solution-दिया है (Given):समकोण \angle ABC त्रिभुज में BD माध्यिका है अर्थात् AD=DC
सिद्ध करना है (To Prove):BD=\frac{1}{2} AC
रचना (Construction):AC के मध्य बिन्दु D से DE \parallel BC खींची जो AB को E पर मिलती है।
उपपत्ति (Proof):D,AC का मध्य बिन्दु है तथा DE \parallel BC
अतः मध्य बिन्दु प्रमेय विलोम से
BE=AE ……(1)
\angle AED=\angle ABC(संगत कोण)
अतः \angle AED=\angle BED=90^{\circ}....(2)
\triangle AED तथा \triangle BED में
DE=DE (उभयनिष्ठ भुजा)
\angle AED=\angle BED [(2) से]
AE=BE [(1) से]
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle AED \cong \triangle BED
AD=BD (सर्वांगसम त्रिभुजों की संगत भुजाएं समान होती है)
अतः BD=\frac{1}{2} AC
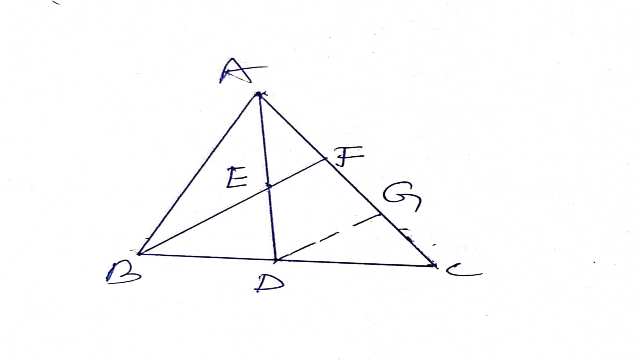
Example-7.E एक \triangle ABC की माध्यिका AD का मध्य बिन्दु है तथा BE को AC को F पर मिलने के लिए बढ़ाया गया है।दर्शाइए कि AF=\frac{1}{3} AC है।
Solution-दिया है (Given):\triangle ABC की माध्यिका AD का मध्य बिन्दु E है।
सिद्ध करना है (To Prove):AF=\frac{1}{3} AC
रचना (Construction):EF \parallel DG खींची।
उपपत्ति (Proof): \triangle BCF में
D,BC का मध्य बिन्दु है
तथा DG \parallel EF (रचना से) अतः मध्य बिन्दु प्रमेय के विलोम से
CG=FG ……..(1)
\triangle ADG में
E,AD का मध्य बिन्दु है तथा DG \parallel EF अतः मध्य बिन्दु प्रमेय के विलोम से
AF=FG …….(2)
(1) व (2) से-
CG=FG=AF
\Rightarrow AF=\frac{1}{3} AC
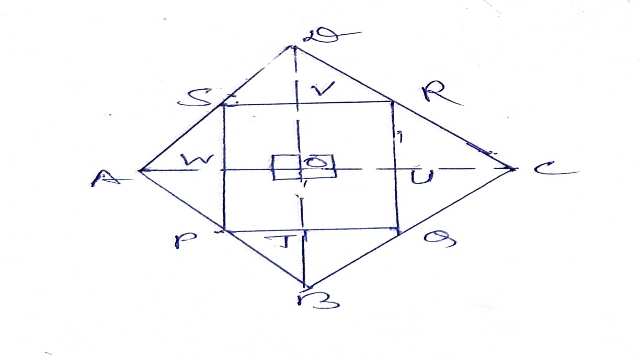
Example-8.दर्शाइए कि किसी वर्ग की क्रमागत भुजाओं के मध्य-बिन्दुओं को मिलाने पर बना चतुर्भुज भी एक वर्ग होता है।
Solution-दिया है (Given): ABCD एक वर्ग है तथा P,Q,R,S वर्ग की क्रमशः भुजाओं AB,BC,CD,DA के मध्य बिन्दु है।
सिद्ध करना है (To Prove):PQRS एक वर्ग है।
रचना (Construction):कर्ण AC व BD को मिलाया जो O पर काटते हैं।
उपपत्ति (Proof): \triangle ACD में S व R भुजाओं AD व CD के मध्य बिन्दु हैं अतः मध्य बिन्दु प्रमेय से
SR=\frac{1}{2} AC....(1) \\ SR \parallel AC
इसी प्रकार \triangle ABC में P व Q क्रमशः भुजाओं AB व BC के मध्य बिन्दु हैं अतः
PQ=\frac{1}{2} AC...(3) \\ PQ \parallel AC....(4)
(1) व (3) तथा (2) व (4) से-
\frac{1}{2} AC =SR=PQ तथा SR \parallel AC.....(5)
में P व S क्रमशः भुजाओं AB व AD के मध्य बिन्दु हैं
SP=\frac{1}{2} BD.....(6) तथा SP \parallel BD.....(7)
इसी प्रकार \triangle BCD में Q व R क्रमशः भुजाओं BC व CD के मध्य बिन्दु हैं अतः
QR=\frac{1}{2} BD.....(8) \\ QR \parallel BD.....(9)
(6) व (8) तथा (7) व (9) से-
SP=QR=\frac{1}{2} BD......(10)
SP \parallel QR परन्तु AC=BD ….(11)
(5) व (10) तथा (11) से-
SP=PQ=QR=RS …….(12)
तथा PQRS एक समान्तर चतुर्भुज है।
चतुर्भुज SWOV में SV \parallel OW तथा OV \parallel SW
अतः SWOV समान्तर चतुर्भुज है।फलत:
\angle RSP=\angle AOD=90^{\circ}(स.च. के सम्मुख कोण बराबर होते हैं)….(13)
इसी प्रकार \angle SPQ=\angle PQR=\angle QRS=90^{\circ}....(4)
समीकरण (12),(13) व (14) से-
PQRS एक वर्ग है।
3.मध्य बिन्दु प्रमेय की समस्याएं (Mid Point Theorem Problems),मध्य बिन्दु प्रमेय सवाल (Mid Point Theorem Questions)-
(1.)एक समबाहु त्रिभुज की भुजाओं BC,CA और AB के मध्य-बिन्दु क्रमशः D,E और F है।सिद्ध कीजिए कि \triangle DEF एक समबाहु त्रिभुज है।
(2.)सिद्ध कीजिए कि एक समलम्ब चतुर्भुज के विकर्ण के मध्य बिन्दुओं को मिलाने वाली रेखा उसकी समान्तर भुजाओं के समान्तर तथा उनके अन्तर की आधी होगी।
(3.) सिद्ध कीजिए कि किसी चतुर्भुज की क्रमागत भुजाओं के मध्य बिन्दुओं को मिलाने से बना चतुर्भुज समान्तर चतुर्भुज होता है।
(4.)चित्र में X और Y क्रमशः समान्तर चतुर्भुज ABCD की सम्मुख भुजाओं AD और BC के मध्य-बिन्दु हैं।साथ ही BX और DY क्रमशः AC को P और Q पर प्रतिच्छेद करते हैं।दर्शाइए कि AP=PQ=QC है।
उपर्युक्त सवालों को हल करने पर मध्य बिन्दु प्रमेय (Mid Point Theorem),मध्य बिन्दु प्रमेय कक्षा 9 (Mid Point Theorem Class 9) को ठीक से समझा जा सकता है।
Also Read This Article:-Plane Geometry and Line and Angle
4.मध्य बिन्दु प्रमेय (Mid Point Theorem) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.आप मध्य बिंदु प्रमेय को कैसे हल करते हैं? (How do you solve mid point theorem?)
उत्तर-एक त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समानांतर और लम्बाई में तीसरी भुजा के आधे के बराबर होता है।
प्रश्न:2.चतुर्भुज में मध्य बिंदु प्रमेय क्या है? (What is Mid Point Theorem in Quadrilateral?),चतुर्भुज मध्यबिंदु प्रमेय (Quadrilateral Midpoint Theorem)
उत्तर-एक स्वेच्छ चतुर्भुज की भुजाओं के मध्य बिंदु एक समानांतर चतुर्भुज बनाते हैं।यदि चतुर्भुज उत्तल या अवतल (सम्मिश्र नहीं) है,तो समांतर चतुर्भुज का क्षेत्रफल चतुर्भुज का आधा क्षेत्रफल है।
प्रश्न:3.क्या हम BPT का उपयोग करके मध्य बिंदु प्रमेय साबित कर सकते हैं? (Can we Prove Mid Point Theorem by Using BPT?)
उत्तर-साथ ही, मध्य-बिंदु प्रमेय का विलोम भी सही है,जो बताता है कि एक त्रिभुज के एक भुजा के मध्य-बिंदु से खींची गई रेखा जो अन्य भुजा के समानांतर होती है,त्रिभुज की तीसरी भुजा को समद्विभाजित करती है।इसलिए आधारभूत आनुपातिकता प्रमेय सिद्ध है।
प्रश्न:4.आप मिडपॉइंट प्रमेय के विलोम को कैसे साबित करते हैं? (How do you Prove the Converse of the Midpoint Theorem?)
उत्तर-मिडपॉइंट प्रमेय का विलोम बताता है कि “यदि एक रेखा किसी त्रिभुज के एक भुजा के मध्य बिंदु के माध्यम से खींची जाती है और अन्य भुजा के समानांतर होती है,तो यह तीसरी भुजा को समद्विभाजित करती है।
जैसे-∆PQR में S,PQ का मध्य बिंदु है और ST,QR के समानांतर खींची जाती है तो PT=TR होगा।
प्रश्न:5.मिडपॉइंट प्रमेय ग्रेड 10 (Midpoint Theorem Grade 10),मध्य-बिंदु प्रमेय कक्षा 10 (Mid-Point Theorem Class 10)
उत्तर-मध्यबिंदु प्रमेय में कहा गया है कि “त्रिभुज के दो भुजाओं के मध्य बिंदु को मिलाने वाला रेखाखंड इसकी तीसरी भुजा के समानांतर होता है और आधा भी है।
उपर्युक्त प्रश्नों के उत्तर द्वारा मध्य बिन्दु प्रमेय (Mid Point Theorem),मध्य बिन्दु प्रमेय कक्षा 9 (Mid Point Theorem Class 9) को भली-भांति समझा जा सकता है।
है और आधा भी है।
उपर्युक्त प्रश्नों के उत्तर द्वारा मध्य बिन्दु प्रमेय (Mid Point Theorem),मध्य बिन्दु प्रमेय कक्षा 9 (Mid Point Theorem Class 9) को भली-भांति समझा जा सकता है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |