1.त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules)-

त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) में एक त्रिभुज के तीनों कोण से दूसरे त्रिभुज के तीनों कोण बराबर होने पर दोनों त्रिभुजों का सर्वांगसम होना आवश्यक नहीं है।
(1.)भुजा-भुजा-भुजा सर्वांगसमता नियम (SSS Property Rule)-
यदि एक त्रिभुज की तीनों भुजाएं दूसरे त्रिभुज की तीनों संगत भुजाओं के बराबर हो तो दोनों त्रिभुज सर्वांगसम होते हैं।

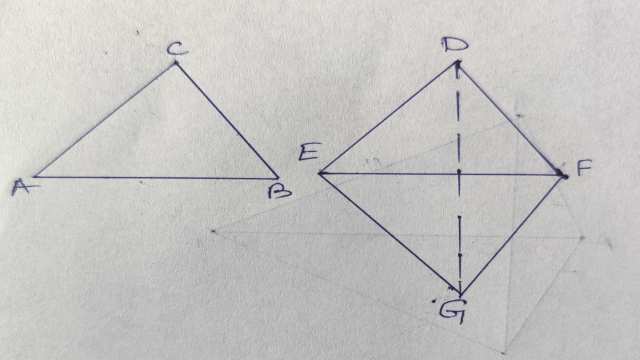
दिया है (Given): \triangle ABC \text { एवं } \triangle DEF की संगत भुजाएं समान है। अर्थात् AB=DE;BC=EF एवं AC=DF
सिद्ध करना है (To Prove):\triangle ABC \cong \triangle DEF
रचना:\triangle DEF के दूसरी ओर रेखाखण्ड EG इस प्रकार खींचा कि EG=AB हो एवं \angle ABC = \angle FEG हो।GF एवं DG को मिलाया।
उपपत्ति (Proof): \triangle ABC \text { एवं } \triangle GEF में
AB=GE (रचना से)
\angle ABC = \angle GEF (रचना से)
BC=EF(दिया है)
अर्थात् भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ABC \cong \triangle GEF \\ \angle A=\angle G तथा AC=GF …….(1)
(सर्वांगसम त्रिभुजों के संगत कोण एवं संगत भुजाएं बराबर होती है)
अब AB=EG (रचना से) एवं AC=DF (दिया है)
अतः EG=DE ……..(2)
इसी प्रकार AC=GF [समीकरण (1) से]
एवं AC=DF (दिया है)
अतः GF=DF ……….(3)
अर्थात् \triangle EDG में समान भुजाओं EG एवं DE के सम्मुख कोण समान होंगे

\angle EDG= \angle EGD....(4)

इसी प्रकार \triangle FDG में समान भुजाओं GF एवं DF के सम्मुख कोण समान होंगे

\angle GDF=\angle DGF......(5)
(4) व (5) से

\angle EDG+\angle GDF=\angle EGD + \angle DGF \\ \Rightarrow  \angle D= \angle G .....(6)
परन्तु समीकरण (1) से

\angle A= \angle G .....(7)
अर्थात् (6) व (7) से

\angle A= \angle D .....(8)
अतः \triangle ABC \text { एवं } \triangle DEF के लिए
AB=DE (दिया है)
\angle A= \angle D [(8) से]
AC=DF (दिया है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABC \cong \triangle DEF
यदि बराबर भुजाओं का ध्यान रखकर एक त्रिभुज को दूसरे त्रिभुज पर रखते हैं तो एक त्रिभुज दूसरे त्रिभुज को ढक लेता है।यह तभी संभव है जब दोनों त्रिभुज सर्वांगसम हों।
(2.)समकोण-कर्ण-भुजा सर्वांगसमता (RHS Congruence Property):
यदि दो समकोण त्रिभुजों में एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हो तो त्रिभुज सर्वांगसम होते हैं।
R-Right Angle (समकोण),H-Hypotenuse (कर्ण),S-Side (भुजा) को दर्शाता है।

दिया है (Given):दो समकोण \triangle ABC \text { एवं } \triangle DEF \text { में } \angle B= \angle E=90° है। कर्ण AC=कर्ण DF एवं भुजा AB=भुजा DE
सिद्ध करना है (To Prove):\triangle ABC \cong \triangle DEF
रचना: \triangle DEF में E को G तक आगे इस प्रकार बढ़ाया कि GE=BC हो एवं G को D से मिलाया।
उपपत्ति (Proof): यहां \angle DEF=90° है अतः \angle DEG=90° होगा।….(1)
अब \triangle ABC \text { एवं } \triangle DEG में
AB=DE (दिया है)
BC=GE (रचना से)
\angle ABC = \angle DEG=90° [(1) से]
अर्थात् भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABC \cong \triangle DEG
अतः AC=DG एवं \angle C = \angle G……..(2)
(सर्वांगसम त्रिभुजों की संगत भुजाएं एवं संगत कोण बराबर होते हैं)
परन्तु दिया हुआ है कि AC=DF ….(3)
(2) व (3) से
DG=DF ………(4)
\therefore \angle G= \angle F (\triangle DGF  में बराबर भुजाओं (DG=DF) के सम्मुख कोण समान होंगे)….(5)
(2) व (5) से

\angle C = \angle F.....(6)
अब \triangle ABC \text { एवं } \triangle DEF \text { में }
AB=DE (दिया है)
\angle C = \angle F [(6) से]
एवं \angle ABC = \angle DEF=90° (दिया है)
अर्थात् कोण-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABC \cong \triangle DEF
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Properties of Triangles class 9

2.त्रिभुजों की सर्वांगसमता के उदाहरण (Congruence of Triangles Examples),सर्वांगसम त्रिभुजों के नियम के उदाहरण (Congruent Triangles Rules Examples)-

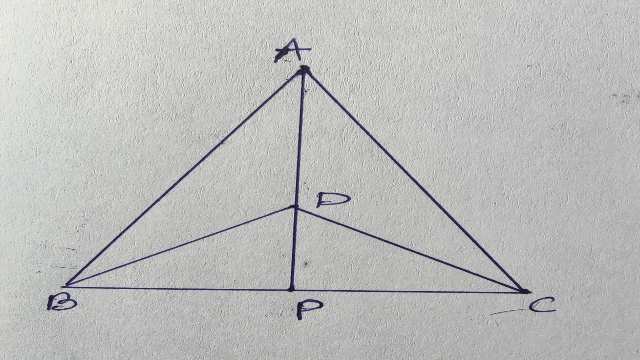
Example-1.\triangle ABC \text { और } \triangle DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं।यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे तो दर्शाइए कि
(i)\triangle ABD \cong \triangle ACD
(ii)\triangle ABP \cong \triangle ACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
Solution-

दिया है (Given): \triangle ABC \text { तथा  } \triangle DBC समद्विबाहु त्रिभुज है अर्थात् AB=AC व \angle ABC = \angle ACB तथा BD=DC व  \angle DBP = \angle DCP
सिद्ध करना है (To Prove):
(i) \triangle ABD \cong \triangle ACD
(ii) \triangle ABP \cong \triangle ACP
(iii)AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
उपपत्ति (Proof): \angle ABC = \angle ACB (दिया है)....(1) \\ \angle DBP = \angle DCP (दिया है)….(2)
(1) में से (2) घटाने पर-

\angle ABC - \angle DBP =\angle ACB - \angle DCP \\ \angle ABD=\angle ACD....(3) \\ \triangle ABD \text { एवं } \triangle ACD  \text { में }
AB=AC (दिया है)
\angle ABD=\angle ACD [(3) से]
BD=DC (दिया है)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABD \cong \triangle ACD \\ (ii) \angle BAD=\angle CAD
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\triangle ABP \text { तथा  } \triangle ACP में
AB=AC (दिया है)
\angle BAD=\angle CAD [(4) से]
AP=AP (उभयनिष्ठ है)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABP \cong \triangle ACP
(iii) BP=PC
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
\triangle BDP \text { तथा  } \triangle CDP में
BD=DC (दिया है)
DP=DP (उभयनिष्ठ है)
BP=PC [(5) से]
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle BDP \cong \triangle CDP \\  \angle BDP=\angle CDP \\ \angle BPD=\angle CPD.....(6)
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\angle BAD=\angle CAD व \angle BPD=\angle CPD
अतः AP , \angle A \text { और } \angle D दोनों को समद्विभाजित करता है।
(iv) \angle BPA + \angle CPA =180° (रैखिक कोण युग्म से)
\angle BPD=\angle CPD [(6) से]
अतः \angle BPA = \angle CPA =90°
BP=PC [(5) से]
अतः AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

उपर्युक्त उदाहरण के द्वारा त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को समझ सकते हैं।
Example-2.AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है जिसमें AB=AC है।दर्शाइए कि
(i)AD रेखाखण्ड BC को समद्विभाजित करता है।
(ii)AD कोण A को समद्विभाजित करता है।
Solution-

दिया है (Given): \triangle ABC \text { में } AD \perp BC
सिद्ध करना है (To Prove):(i) AD रेखाखण्ड BC को समद्विभाजित करता है अर्थात् BD=DC
(ii)AD \angle A को समद्विभाजित करता अर्थात् \angle BAD=\angle CAD
उपपत्ति (Proof): \triangle ABD \text { तथा } \triangle ACD में
AB=AC (दिया है)
AD=AD (उभयनिष्ठ है)
\angle ADB = \angle ADC =90° (दिया है)
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (By RHS Congruence Property)

\triangle ABD \cong \triangle ACD \\ BD=DC \\ \angle BAD =\angle CAD
(सर्वांगसम त्रिभुजों की संगत भुजाएं और संगत कोण बराबर होते हैं)

उपर्युक्त उदाहरण के द्वारा त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को समझ सकते हैं।
Example-3.एक त्रिभुज ABC की दो भुजाएं AB और BC तथा माध्यमिका AM क्रमशः एक दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यमिका PN के बराबर है।दर्शाइए कि

(i)\triangle ABM \cong \triangle PQN \\ (ii) \triangle ABC \cong \triangle PQR
Solution-

दिया है (Given): \triangle ABC \text { तथा } \triangle PQR में AB=PQ,BC=QR तथा माध्यमिका AM=AN
सिद्ध करना है (To Prove): (i)\triangle ABM \cong \triangle PQN \\ (ii) \triangle ABC \cong \triangle PQR

उपपत्ति (Proof):BC=QR (दिया है)
BM=QN (AM व PN माध्यमिका है) ….(1)
\triangle ABM \text { तथा } \triangle PQN में
AB=PQ (दिया है)
BM=QN [(1) से]
AN=PN (दिया है)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABM \cong \triangle PQN \\ (ii)\angle B= \angle Q  (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\triangle ABC \text { तथा } \triangle PQR में
AB=PQ (दिया है)
\angle B= \angle Q [(2) से]
BC=QR (दिया है)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABC \cong \triangle PQR

उपर्युक्त उदाहरण के द्वारा त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को समझ सकते हैं।
Example-4.BE और CF एक त्रिभुज ABC के बराबर शीर्षलम्ब है।RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि \triangle ABC एक समद्विबाहु त्रिभुज है।
Solution-

दिया है (Given): \triangle ABC \text { में  } BE \perp AC,CF \perp AB तथा BE=CF
सिद्ध करना है (To Prove): \triangle ABC समद्विबाहु त्रिभुज है अर्थात् AB=AC
उपपत्ति (Proof): \triangle BCF \text { तथा } \triangle CBE में
BC=BC (उभयनिष्ठ है)
CF=BE (दिया है)
\angle BFC = \angle CEB =90° (दिया है)
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (By RHS Congruence Property)

\triangle BCF \cong \triangle CBE \\ \angle B=\angle C
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
AB=AC
(बराबर कोणों की सम्मुख भुजाएं बराबर होती हैं)
अतः \triangle ABC समद्विबाहु त्रिभुज है)

उपर्युक्त उदाहरण के द्वारा त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को समझ सकते हैं।
Example-5.ABC समद्विबाहु त्रिभुज है जिसमें AB=AC है। AP \perp BC  खींचकर दर्शाइए कि \angle B=\angle C है।
Solution-

दिया है (Given): \triangle ABC में AB=AC है।  AP \perp BC हैं।
सिद्ध करना है (To Prove): \angle B=\angle C
उपपत्ति (Proof):  \triangle ABP \text{ तथा } \triangle ACP में
AB=AC (दिया है)
AP=AP (उभयनिष्ठ है)
\angle APB = \angle APC =90° (दिया है)
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (By RHS Congruence Property)

\triangle ABP \cong \triangle ACP \\ \angle B=\angle C
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
उपर्युक्त उदाहरणों के द्वारा त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को समझ सकते हैं।

3.त्रिभुजों की सर्वांगसमता समस्याएं (Congruence of Triangles Problems),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules Problems)-

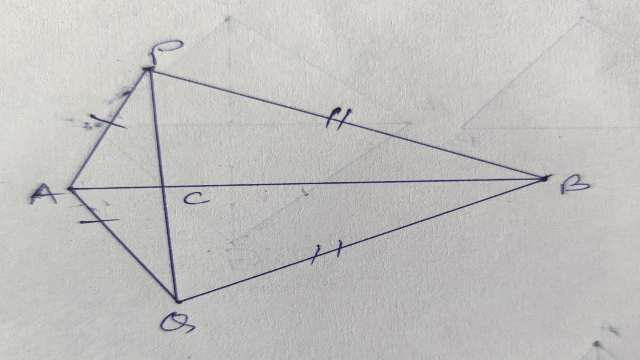
(1.)AB एक रेखाखण्ड है तथा बिन्दु P तथा Q इस रेखाखण्ड AB के विपरीत ओर इस प्रकार स्थित है कि इनमें से प्रत्येक A और B से समदूरस्थ है।दर्शाइए कि रेखा PQ रेखाखण्ड AB का लम्ब समद्विभाजक है।

(2.)बिन्दु A पर प्रतिच्छेद करने वाली दो रेखाओं l और m से समदूरस्थ एक बिन्दु P है।दर्शाइए कि रेखा AP दोनों रेखाओं के बीच के कोण को समद्विभाजित करती है।

उपर्युक्त सवालों को हल करने पर त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को ठीक से समझा जा सकता है।

4.SSS SAS ASA AAS क्या है? (What is SSS SAS ASA AAS?)-

SSS (साइड-साइड-साइड) तीनों संगत भुजाएं एक-दूसरे के सर्वांगसम हैं।SAS एसएएस (साइड-एंगल-साइड) दो भुजाएं और उनके बीच का कोण सर्वांगसम है।ASA एएसए (कोण-साइड-कोण) एक भुजा तथा उस भुजा पर बनने वाले कोण सर्वांगसम हों।AAS एएएस (एंगल-एंगल-साइड) में एक भुजा तथा अन्य दो कोण सर्वांगसम होते हैं।

5.त्रिभुजों में सर्वांगसमता के 4 परीक्षण क्या हैं? (What are the 4 tests of congruence in a triangle?)-

त्रिभुजों की सर्वांगसमता का परीक्षण करने के लिए उपयोग किए जाने वाले इन चार मानदंडों में शामिल हैं: साइड – साइड – साइड (एसएसएस)(SSS Congruence Property), साइड – एंगल – साइड (एसएएस)(SAS Congruence Property), एंगल – साइड – एंगल (एएसए)(ASA Congruence Property),और एंगल – एंगल – साइड (एएएस)(AAS Congruence Property)।त्रिभुजों की सर्वांगसमता को सिद्ध करने के और भी तरीके हैं लेकिन इस पाठ में हम खुद को केवल इन पदों तक सीमित रखेंगे।

6.मुझे SSS SAS ASA AAS कहां मिल सकता है? (Where can I find SSS SAS ASA AAS?)-

दो त्रिभुजों के सर्वांगसम होने के पांच तरीके हैं: एसएसएस, एसएएस, एएसए, एएएस और एचएल।
SSS (साइड, साइड, साइड) SSS “साइड, साइड, साइड” के लिए खड़ा है और इसका मतलब है कि हमारे पास तीनों भुजाओं के साथ दो त्रिभुज समान हैं।
SAS (भुजा, कोण, भुजा)
ASA एएसए (कोण, भुजा, कोण)
AAS एएएस (कोण, कोण, भुजा)
HL एचएल (कर्ण, भुजा)

7.आप कैसे साबित करते हैं कि त्रिभुज सर्वांगसम हैं? (How do you prove triangles are congruent?)-

यदि दो त्रिभुज और एक त्रिभुज के सम्मिलित कोण एक ही भुजा के संगत और दूसरे त्रिभुज के कोण के बराबर हैं, तो त्रिभुज सर्वांगसम होते हैं।

8.त्रिभुजों के सर्वांगसमता के लिए मानदंड कक्षा 9 (Criteria for congruence of triangles class 9)-

त्रिभुजों के सर्वांगसमता के लिए 5 मुख्य नियम हैं:
SSS Criterion: Side-Side-Side.
SAS Criterion: Side-Angle-Side.
ASA Criterion: Angle-Side- Angle.
AAS Criterion: Angle-Angle-Side.
RHS Criterion: Right angle- Hypotenuse-Side.
एसएसएस मानदंड: साइड-साइड-साइड।
एसएएस मानदंड: साइड-एंगल-साइड।
एएसए मानदंड: कोण-पक्ष- कोण।
एएएस मानदंड: कोण-कोण-पक्ष।
आरएचएस मानदंड: समकोण- हाइपोटेन्यूज-साइड।

9.सर्वांगसमता नियम (Congruence rule)-

कहा जाता है कि दो त्रिभुज सर्वांगसम होते हैं यदि अपने सभी तीन भुजाएं और तीन कोणों के बराबर होते हैं। ज्यामितीय आकृतियों के मामले में समान लंबाई वाले रेखा खंड सर्वांगसम होते हैं और समान माप वाले कोण सम्‍मिलित होते हैं। त्रिभुजों की सर्वांगसमता के लिए शर्तें: एसएसएस (साइड-साइड-साइड)
उपर्युक्त उदाहरणों,प्रश्नों के उत्तर तथा सवालों को हल करके त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) को भली-भांति समझ सकते हैं।

Also Read This Article:-Surface Area of Cube and Cuboid

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here