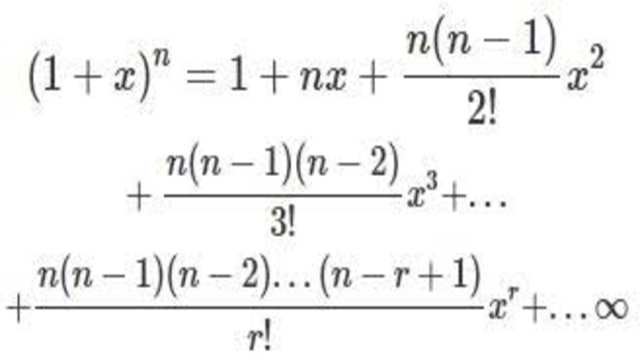Binomial Theorem for Any Index
1.किसी भी घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Any Index)-
- किसी भी घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Any Index) में घातांक धनात्मक, ऋणात्मक,परिमेय हो सकती है।
(1.)आप भिन्नों के साथ द्विपद विस्तार कैसे करते हैं? (How do you do binomial expansion with fractions?)-
- किसी द्विपद में जब घात भिन्नात्मक अथवा ऋणात्मक हो तब इसका प्रसार तभी संभव है जबकि द्विपद का प्रथम पद 1 तथा द्वितीय पद संख्यात्मक रूप में एक से छोटा हो। अर्थात् हम द्विपद को सर्वदा { (1+x) }^{ n } के रूप में रखकर प्रसार करते हैं जहां x का संख्यात्मक मान 1 से कम है अर्थात् -1<x<1 इस स्थिति में द्विपद का प्रसार सूत्र निम्नलिखित है
- { (1+x) }^{ n }=1+nx+\frac { n(n-1) }{ 2! } { x }^{ 2 }+\frac { n(n-1)(n-2) }{ 3! } { x }^{ 3 }+......+\frac { n(n-1)....(n-r+1) }{ r! } { x }^{ r }.....(1)
- यह प्रसार अनन्त श्रेणी का रूप लेती है अर्थात् प्रसार में पदो की संख्या अनन्त होती है।इसको द्विपद सारणी कहते हैं।
{ (x+a) }^{ n } के प्रसार में यदि में x का मान a से कम है।तब तथा यदि a का मान x से कम है तो
{ (x+a) }^{ n }={ a }^{ n }{ (1+\frac { x }{ a } ) }^{ n } के रूप में बदलकर प्रसार करते हैं।
(1.)प्रसार का व्यापक पद (General Term of Expansion)-
- { T }_{ r+1 }=\frac { n(n-1)....(n-r+1) }{ r! } { x }^{ r }
टिप्पणी-जब n एक भिन्न अथवा ऋण राशि हो तब ^{ n }{ { C }_{ r } } निरर्थक है। अतः अलग-अलग पदों के गुणांक ^{ n }{ { C }_{ 1 } },^{ n }{ { C }_{ 2 } }..... नहीं लिखकर उपर्युक्त प्रकार से लिखना चाहिए।
(2.)कुछ महत्त्वपूर्ण प्रसार (Some Important Expansions),परिमेय घातांक प्रमाण के लिए द्विपद प्रमेय (binomial theorem for rational index proof)-
(i){ (1+x) }^{ n }=1+nx+\frac { n(n-1) }{ 2! } { x }^{ 2 }+\frac { n(n-1)(n-2) }{ 3! } { x }^{ 3 }+......+\frac { n(n-1)....(n-r+1) }{ r! } { x }^{ r }.....(1) \\ (ii){ (1-x) }^{ n }=1-nx+\frac { n(n-1) }{ 2! } { x }^{ 2 }+......+{ (-1) }^{ r }\frac { n(n-1)....(n-r+1) }{ r! } { x }^{ r }.....(2)\\ (iii){ (1+x) }^{ -n }=1-nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }+......+{ (-1) }^{ r }\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }.....(3)\\ (iv){ (1-x) }^{ -n }=1+nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }+......+\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }.....(4)
समीकरण (2) तथा (3) में n=1,2,3 रखने पर-
(v){ (1-x) }^{ -1 }=1+x+{ x }^{ 2 }+{ x }^{ 3 }......+{ x }^{ r }+....\\ (vi){ (1+x) }^{ -1 }=1-x+{ x }^{ 2 }-{ x }^{ 3 }......+{ (-1) }^{ r }{ x }^{ r }+....\\ (vii){ (1+x) }^{ -2 }=1-2x+3{ x }^{ 2 }-4{ x }^{ 3 }......+{ (-1) }^{ r }.(r+1){ x }^{ r }+....\\ (viii){ (1-x) }^{ -2 }=1+2x+3{ x }^{ 2 }+4{ x }^{ 3 }......+(r+1){ x }^{ r }+....\\ (ix){ (1+x) }^{ 3 }=1-3x+6{ x }^{ 2 }-10{ x }^{ 3 }......+{ (-1) }^{ r }\frac { (r+1)(r+2) }{ 2! } { x }^{ r }+....\\ (x){ (1-x) }^{ -3 }=1+3x+6{ x }^{ 2 }+10{ x }^{ 3 }......+\frac { (r+1)(r+2) }{ 2! } { x }^{ r }+....
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Mathematical Induction
2.किसी भी घातांक के लिए द्विपद प्रमेय के उदाहरण (Binomial Theorem for Any Index Examples),ऋणात्मक घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Negative Index)-
निम्नलिखित द्विपदों का चार पदों तक प्रसार कीजिए:
Example-1.{ (3-2{ x }^{ 2 }) }^{ -\frac { 2 }{ 3 } }
Solution-{ (3-2{ x }^{ 2 }) }^{ -\frac { 2 }{ 3 } }
सूत्र { (1-x) }^{ -n }=1+nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }+......+\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }\\ ={ (3-2{ x }^{ 2 }) }^{ -\frac { 2 }{ 3 } }\\ ={ [3(1-\frac { 2 }{ 3 } { x }^{ 2 })] }^{ -\frac { 2 }{ 3 } }\\ ={ 3 }^{ -\frac { 2 }{ 3 } }{ (1-\frac { 2 }{ 3 } { x }^{ 2 }) }^{ -\frac { 2 }{ 3 } }\\ ={ 3 }^{ -\frac { 2 }{ 3 } }[1+\frac { 2 }{ 3 } (\frac { 2 }{ 3 } ){ x }^{ 2 }+\frac { (\frac { 2 }{ 3 } )(\frac { 2 }{ 3 } +1) }{ 2! } { (\frac { 2 }{ 3 } { x }^{ 2 }) }^{ 2 }+\frac { (\frac { 2 }{ 3 } )(\frac { 2 }{ 3 } +1)(\frac { 2 }{ 3 } +2) }{ 3! } { (\frac { 2 }{ 3 } { x }^{ 2 }) }^{ 3 }]\\ ={ 3 }^{ -\frac { 2 }{ 3 } }[1+\frac { 4 }{ 9 } { x }^{ 2 }+\frac { 2 }{ 3 } .\frac { 5 }{ 3 } .\frac { 1 }{ 2 } .\frac { 4 }{ 9 } { { x }^{ 4 } }+\frac { 2 }{ 3 } .\frac { 5 }{ 3 } .\frac { 8 }{ 3 }.\frac { 1 }{ 6 } .\frac { 8 }{ 27 } { { x }^{ 6 } }]\\ =(\frac { 1 }{ { 3 }^{ \frac { 2 }{ 3 } } } )[1+\frac { 4 }{ 9 } { x }^{ 2 }+\frac { 20 }{ 81 } { { x }^{ 4 } }+\frac { 320 }{ 2187 } { { x }^{ 6 } }]
Example-2.\frac { 1 }{ \sqrt { (5+4x) } }
Solution–\frac { 1 }{ \sqrt { (5+4x) } } \\ =\frac { 1 }{ { (5+4x) }^{ \frac { 1 }{ 2 } } } \\ ={ (5+4x) }^{ -\frac { 1 }{ 2 } }\\ ={ [5(1+\frac { 4 }{ 5 } x)] }^{ \frac { 1 }{ 2 } }\\ ={ 5 }^{ -\frac { 1 }{ 2 } }{ (1+\frac { 4 }{ 5 } x) }^{ -\frac { 1 }{ 2 } }
सूत्र { (1+x) }^{ -n }=1-nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }-\frac { n(n+1)(n+2) }{ 3! } { x }^{ 3 }+......+{ (-1) }^{ r }\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }\\ ={ 5 }^{ -\frac { 1 }{ 2 } }{ (1+\frac { 4 }{ 5 } x) }^{ -\frac { 1 }{ 2 } }\\ ={ 5 }^{ -\frac { 1 }{ 2 } }[1-(\frac { 1 }{ 2 } )(\frac { 4 }{ 5 } x)+\frac { \frac { 1 }{ 2 } (\frac { 1 }{ 2 } +1) }{ 2 } { (\frac { 4 }{ 5 } x) }^{ 2 }-\frac { \frac { 1 }{ 2 } (\frac { 1 }{ 2 } +1)(\frac { 1 }{ 2 } +2) }{ 3! } { (\frac { 4 }{ 5 } x) }^{ 3 }]\\ ={ 5 }^{ -\frac { 1 }{ 2 } }[1-\frac { 2x }{ 5 } +\frac { 6{ x }^{ 2 } }{ 25 } -\frac { 4{ x }^{ 3 } }{ 25 } ]\\ =\frac { 1 }{ \sqrt { 5 } } [1-\frac { 2x }{ 5 } +\frac { 6{ x }^{ 2 } }{ 25 } -\frac { 4{ x }^{ 3 } }{ 25 } ]
निम्नलिखित प्रसारों में वांछित पद ज्ञात कीजिए:
Example-3. { (1-3x) }^{ -\frac { 1 }{ 3 } } का चौथा पद
Solution– { (1-3x) }^{ -\frac { 1 }{ 3 } } का चौथा पद
{ (1-x) }^{ -n } के प्रसार में व्यापक पद
{ T }_{ r+1 }=\frac { n(n+1)(n+2)....(n+r-1) }{ r! } { x }^{ r }
दिए गए द्विपद में n=\frac { 1 }{ 3 } तथा x के स्थान पर 3x रखने एवं r=3 रखने पर द्विपद के प्रसार में चौथा पद
{ T }_{ 4 }=\frac { \frac { 1 }{ 3 } (\frac { 1 }{ 3 } +1)(\frac { 1 }{ 3 } +2) }{ 3! } { (3x) }^{ 3 }\\ \Rightarrow { T }_{ 4 }=\frac { \frac { 1 }{ 3 } \times \frac { 4 }{ 3 } \times \frac { 7 }{ 3 } }{ 6 } { 27x }^{ 3 }\\ \Rightarrow { T }_{ 4 }=\frac { 14 }{ 3 } { x }^{ 3 }
Example-4.{ (1+x) }^{ \frac { 5 }{ 2 } } का सातवां पद
Solution– { (1+x) }^{ \frac { 5 }{ 2 } } का सातवां पद
{ (1+x) }^{ n } के प्रसार में व्यापक पद
{ T }_{ r+1 }=\frac { n(n-1)(n-2)....(n-r+1) }{ r! } { x }^{ r }
दिए गए द्विपद में n=\frac { 5 }{ 2 } तथा x के स्थान पर x एवं r=6 रखने पर द्विपद के विस्तार में सातवां पद
{ T }_{ 7 }=\frac { \frac { 5 }{ 2 } (\frac { 5 }{ 2 } -1)(\frac { 5 }{ 2 } -2)(\frac { 5 }{ 2 } -3)(\frac { 5 }{ 2 } -4)(\frac { 5 }{ 2 } -5) }{ 6! } { x }^{ 6 }\\ \Rightarrow { T }_{ 7 }=\frac { \frac { 5 }{ 2 } (\frac { 3 }{ 2 } )(\frac { 1 }{ 2 } )(-\frac { 1 }{ 2 } )(-\frac { 3 }{ 2 } )(-\frac { 5 }{ 2 } ) }{ 6\times 5\times 4\times 3\times 2\times 1 } { x }^{ 6 }\\ \Rightarrow { T }_{ 7 }=-\frac { 5 }{ 1024 } { x }^{ 6 }
निम्नलिखित प्रसारों का व्यापक पद ज्ञात कीजिए:
Example-5.{ (1-2x) }^{ -\frac { 3 }{ 2 } }
Solution–{ (1-2x) }^{ -\frac { 3 }{ 2 } }
{ (1-x) }^{ -n } के प्रसार में व्यापक पद
{ T }_{ r+1 }=\frac { n(n+1)(n+2)....(n+r-1) }{ r! } { x }^{ r }
दिए गए द्विपद में n=\frac { 3 }{ 2 } तथा x के स्थान पर 2x है। अतः { (1-2x) }^{ -\frac { 3 }{ 2 } } के विस्तार में व्यापक पद
{ T }_{ r+1 }=\frac { \frac { 3 }{ 2 } (\frac { 3 }{ 2 } +1)(\frac { 3 }{ 2 } +2).........(\frac { 3 }{ 2 } +r-1) }{ r! } { (2x })^{ r }\\ \Rightarrow { T }_{ r+1 }=\frac { \frac { 3 }{ 2 } .\frac { 5 }{ 2 } .\frac { 7 }{ 2 } ...........(\frac { 2r+1 }{ 2 } ) }{ r! } { 2 }^{ r }{ x }^{ r }\\ \Rightarrow { T }_{ r+1 }=\frac { 3.5.7..........(2r+1) }{ { 2 }^{ r }r! } { 2 }^{ r }{ x }^{ r }\\ \Rightarrow { T }_{ r+1 }=\frac { 3.5.7..........(2r+1) }{ r! } { x }^{ r }
Example-6.{ (1-x) }^{ -\frac { p }{ q } }
Solution–{ (1-x) }^{ -\frac { p }{ q } }
{ (1-x) }^{ -n } के प्रसार में व्यापक पद-
{ T }_{ r+1 }=\frac { n(n+1)(n+2)....(n+r-1) }{ r! } { x }^{ r }
दिए गए द्विपद में n=\frac { p }{ q } तथा x के स्थान पर x है। अतः { (1-x) }^{ -\frac { p }{ q } } के विस्तार में व्यापक पद:
{ T }_{ r+1 }=\frac { \frac { p }{ q } (\frac { p }{ q } +1)(\frac { p }{ q } +2).........(\frac { p }{ q } +r-1) }{ r! } { (x })^{ r }\\ { T }_{ r+1 }=\frac { \frac { p }{ q } (\frac { p+q }{ q } )(\frac { p+2q }{ q } ).........(\frac { p+qr-q }{ q } ) }{ r! } { (x })^{ r }\\ { T }_{ r+1 }=\frac { p(p+q)(p+2q)(p+3q).....(p+qr-q) }{ r! } (\frac { x }{ q } )^{ r }\\ { T }_{ r+1 }=\frac { p(p+q)(p+2q)(p+3q).....(p+(r-1)q) }{ r! } { (\frac { x }{ q } })^{ r }
Example-7.यदि x<3 हो तो { (3-x) }^{ -8 } के प्रसार में का गुणांक ज्ञात कीजिए।
Solution– { (3-x) }^{ -8 } के प्रसार में { x }^{ 5 } का गुणांक
={ [3(1-\frac { x }{ 3 } )] }^{ -8 }\\= { 3 }^{ -8 }{ [(1-\frac { x }{ 3 } )] }^{ -8 }
{ 3 }^{ -8 }{ [(1-\frac { x }{ 3 } )] }^{ -8 } का (r+1) वां पद =
={ 3 }^{ -8 }\frac { (-8)(-8-1)(-8-2)(-8-3)......(-8-r+1) }{ r! } (\frac { x }{ 3 } )^{ r }\\ ={ 3 }^{ -8 }{ (-1) }^{ r }\frac { 8.9.10.11............(r+7) }{ r! } (\frac { x }{ 3 } )^{ r }
अतः { x }^{ 5 } का गुणांक={ 3 }^{ -8 }{ (-1) }^{ 5 }\frac { 8.9.10.11.12 }{ 5! } (\frac { 1 }{ 3 } )^{ 5 }\\ ={ 3 }^{ -8 }{ (-1) }^{ 5 }\frac { 8.9.10.11.12 }{ 5\times 4\times 3\times 2\times 1 } (\frac { 1 }{ 3 } )^{ 5 }\\ =-\frac { 88 }{ { 3 }^{ 11 } }
Example-8.\frac { 1+3{ x }^{ 2 } }{ { (1-{ x }^{ 2 }) }^{ 3 } } के प्रसार में { x }^{ 10 } का गुणांक ज्ञात कीजिए।
Solution–\frac { 1+3{ x }^{ 2 } }{ { (1-{ x }^{ 2 }) }^{ 3 } } के प्रसार में { x }^{ 10 } का गुणांक
=(1+3{ x }^{ 2 }){ (1-{ x }^{ 2 }) }^{ -3 }\\ =(1+3{ x }^{ 2 })(1+3{ x }^{ 2 }+6{ ({ x }^{ 2 }) }^{ 2 }+10{ ({ x }^{ 2 }) }^{ 3 }+15{ ({ x }^{ 2 }) }^{ 4 }+21{ ({ x }^{ 2 }) }^{ 5 }+........)\\ =(1+3{ x }^{ 2 })(1+3{ x }^{ 2 }+6{ x }^{ 4 }+10{ x }^{ 6 }+15{ x }^{ 8 }+21{ x }^{ 10 }+........)\\ =1+(3+3){ x }^{ 2 }+(6+9){ x }^{ 4 }+(10+18){ x }^{ 6 }+(15+30){ x }^{ 8 }+(21+45){ x }^{ 10 }+........\\ =1+6{ x }^{ 2 }+15{ x }^{ 4 }+28{ x }^{ 6 }+45{ x }^{ 8 }+66{ x }^{ 10 }+........
{ x }^{ 10 } का गुणांक=66
Example-9.{ (1-2x+3{ x }^{ 2 }-4{ x }^{ 3 }+......) }^{ n } के विस्तार में { x }^{ 10 } का गुणांक ज्ञात कीजिए तथा यदि x=\frac { 1 }{ 2 } और हो तो व्यंजक का मान ज्ञात कीजिए।
Solution–{ (1-2x+3{ x }^{ 2 }-4{ x }^{ 3 }+......) }^{ n } \\ ={ [{ (1+x) }^{ -2 }] }^{ n }\\ ={ (1+x) }^{ -2n }
{ (1+x) }^{ -2n } के विस्तार में व्यापक पद:
(r+1) वां पद={ (-1) }^{ r }\frac { 2n(2n+1)(2n+2)(2n+3)....(2n+r-1) }{ r! } { x }^{ r }
{ x }^{ r } का गुणांक= { (-1) }^{ r }\frac { 2n(2n+1)(2n+2)(2n+3)....(2n+r-1) }{ r! }
यदि x=\frac { 1 }{ 2 } और n=1 हो तो व्यंजक का मान-
{ (1+x) }^{ -2n }\\ ={ (1+\frac { 1 }{ 2 } ) }^{ -2 }\\ ={ (\frac { 3 }{ 2 } ) }^{ -2 }\\ =\frac { 4 }{ 9 }
Example-10.सिद्ध कीजिए { (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) }^{ 2 }=1+2x+3{ x }^{ 2 }+.....
Solution– { (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) }^{ 2 }\\ { [{ (1+x) }^{ -1 }] }^{ 2 }\\ ={ (1+x) }^{ -2 } \\ \Rightarrow { (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) }^{ 2 }={ (1+x) }^{ -2 }.....(1)
सूत्र { (1-x) }^{ -n }=1+nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }+......+\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }+.....
n=2 रखने पर-
{ (1+x) }^{ -2 }=1+2x+3{ x }^{ 2 }+4{ x }^{ 3 }+.....(2)
समीकरण (1) व (2) से-
{ (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) }^{ 2 }=1+2x+3{ x }^{ 2 }+.....
Example-11.सिद्ध कीजिए (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) (1+3x+6{ x }^{ 2 }+....)={ (1+2x+3{ x }^{ 2 }+.....) }^{ 2 }
Solution– (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) (1+3x+6{ x }^{ 2 }+....)={ (1+2x+3{ x }^{ 2 }+.....) }^{ 2 }
L.H.S= (1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) (1+3x+6{ x }^{ 2 }+....)\\ ={ (1+x) }^{ -1 }{ (1+x) }^{ -3 }\\ [\because 1+x+{ x }^{ 2 }+{ x }^{ 3 }+...={ (1+x) }^{ -1 } तथा (1+3x+6{ x }^{ 2 }+....)={ (1+x) }^{ -3 }]\\ ={ (1+x) }^{ -4 }
सूत्र { (1-x) }^{ -n }=1+nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }+......+\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }+.....
n=4 रखने पर-
{ (1-x) }^{ -4 }=1+4x+\frac { 4(4+1) }{ 2! } { x }^{ 2 }+\frac { 4(4+1)(4+2) }{ 3! } { x }^{ 3 }+......\\ =1+4x+10{ x }^{ 2 }+\frac { 4(5)(6) }{ 3\times 2 } { x }^{ 3 }+......\\ \Rightarrow { (1-x) }^{ -4 }=1+4x+10{ x }^{ 2 }+20{ x }^{ 3 }+......(1)
R.H.S= { (1+2x+3{ x }^{ 2 }+.....) }^{ 2 }\\ ={ [{ (1+x) }^{ -2 }] }^{ 2 }[\because { (1+x) }^{ -2 }=1+2x+3{ x }^{ 2 }+4{ x }^{ 3 }+....(r+1){ x }^{ r }+.....]\\ ={ (1+x) }^{ -4 }.....(2)
समीकरण (1) व (2) से-
(1+x+{ x }^{ 2 }+{ x }^{ 3 }+....) (1+3x+6{ x }^{ 2 }+....)={ (1+2x+3{ x }^{ 2 }+.....) }^{ 2 }
Example-12. यदि x=2y+3{ y }^{ 2 }+4{ y }^{ 3 }+...... है तो y को x की आरोही घातों की श्रेणी के रूप में व्यक्त कीजिए।
Solution–x=2y+3{ y }^{ 2 }+4{ y }^{ 3 }+......
दोनों पक्षों में 1 जोड़ने पर-
1+x=1+2y+3{ y }^{ 2 }+4{ y }^{ 3 }+......\\ \Rightarrow 1+x={ (1-y) }^{ -2 }
[सूत्र \because { (1+x) }^{ -2 }=1+2x+3{ x }^{ 2 }+4{ x }^{ 3 }+....(r+1){ x }^{ r }+..... से]
\Rightarrow { (1+x) }^{ -\frac { 1 }{ 2 } }=1-y\\ \Rightarrow y=1-{ (1+x) }^{ -\frac { 1 }{ 2 } }....(1)\\ { (1+x) }^{ -n }=1-nx+\frac { n(n+1) }{ 2! } { x }^{ 2 }-\frac { n(n+1)(n+2) }{ 3! } { x }^{ 3 }+......+{ (-1) }^{ r }\frac { n(n+1)....(n+r-1) }{ r! } { x }^{ r }+.....
n=\frac { 1 }{ 2 } रखने पर-
\Rightarrow { (1+x) }^{ -\frac { 1 }{ 2 } }=1-\frac { 1 }{ 2 } x+\frac { \frac { 1 }{ 2 } (\frac { 1 }{ 2 } +1) }{ 2! } { x }^{ 2 }-\frac { \frac { 1 }{ 2 } (\frac { 1 }{ 2 } +1)(\frac { 1 }{ 2 } +2) }{ 3! } { x }^{ 3 }+......+{ (-1) }^{ r }\frac { \frac { 1 }{ 2 } (\frac { 1 }{ 2 } +1)....(\frac { 1 }{ 2 } +r-1) }{ r! } { x }^{ r }+.....\\ =1-\frac { x }{ 2 } +\frac { 1 }{ 2 } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } { x }^{ 2 }-\frac { 1 }{ 2 } .\frac { 3 }{ 2 } .\frac { 5 }{ 2 } .\frac { 1 }{ 6 } { x }^{ 3 }+.....+{ (-1) }^{ r }\frac { \frac { 1 }{ 2 } (\frac { 3 }{ 2 } )....(r-\frac { 1 }{ 2 } ) }{ r! } { x }^{ r }\\ \Rightarrow { (1+x) }^{ -\frac { 1 }{ 2 } }=1-\frac { x }{ 2 } +\frac { 3 }{ 8 } { x }^{ 2 }-\frac { 5 }{ 16 } { x }^{ 3 }+........(2)
समीकरण (2) से (1) में मान रखने पर-
\Rightarrow y=1-[1-\frac { x }{ 2 } +\frac { 3 }{ 8 } { x }^{ 2 }-\frac { 5 }{ 16 } { x }^{ 3 }+.....]\\ \Rightarrow y=1-1+\frac { x }{ 2 } -\frac { 3 }{ 8 } { x }^{ 2 }+\frac { 5 }{ 16 } { x }^{ 3 }-.....\\ \Rightarrow y=\frac { x }{ 2 } -\frac { 3 }{ 8 } { x }^{ 2 }+\frac { 5 }{ 16 } { x }^{ 3 }-.....
उपर्युक्त उदाहरणों द्वारा किसी भी घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Any Index), ऋणात्मक घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Negative Index) को समझ सकते हैं।
3.किसी भी घातांक के लिए द्विपद प्रमेय की समस्याएं (Binomial Theorem for Any Index Problems),ऋणात्मक घातांक के लिए द्विपद प्रमेय की समस्याएं (Binomial Theorem for Negative Index Problems)-
- निम्न द्विपदों का चार पदों तक प्रसार कीजिए:
(1){ (1+{ x }^{ 2 }) }^{ -2 }
(2){ (1-\frac { x }{ 2 } ) }^{ \frac { 1 }{ 2 } }
- निम्नलिखित प्रसार में वांछित पद ज्ञात कीजिए:
(3.) (1+2x)^{ -\frac { 1 }{ 2 } } का आठवां पद
(4.) { (1+2x) }^{ 6 }{ (1-x) }^{ 7 } के प्रसार के गुणनफल में { x }^{ 5 } का गुणांक ज्ञात कीजिए।
(5.){ (2x-\frac { 3 }{ { x }^{ 2 } } ) }^{ 7 } के विस्तार में { x }^{ -8 } का गुणांक ज्ञात कीजिए।
(6.){ (a+2b{ x }^{ 2 }) }^{ -3 } के प्रसार में { x }^{ 5 } का गुणांक ज्ञात कीजिए।
- निम्नलिखित प्रसार का व्यापक पद ज्ञात कीजिए:
(7){ ({ a }^{ 3 }-{ x }^{ 3 }) }^{ \frac { 2 }{ 3 } }
(8.) यदि { (1+2x) }^{ 2n } के प्रसार में दूसरे,तीसरे और चौथे पदों के गुणांक समान्तर श्रेढ़ी में हैं तो सिद्ध कीजिए कि 2{ x }^{ 2 }-9x+7=0
- उत्तर-(1)1-2{ x }^{ 2 }+3{ x }^{ 4 }-4{ x }^{ 6 }
(2)1-\frac { x }{ 4 } +\frac { { x }^{ 2 } }{ 32 } -\frac { { x }^{ 3 } }{ 128 }
(3)-\frac { 429 }{ 16 } { x }^{ 7 }
(4.)171
(5.) -20412
(6)-80{ a }^{ -6 }{ b }^{ 3 }
(7)-\frac { 2.1.4.........(3r-5) }{ { 3 }^{ r }r! } .\frac { { x }^{ 3r } }{ { a }^{ 3r-2 } }
- उपर्युक्त सवालों को हल करने पर किसी भी घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Any Index),ऋणात्मक घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Negative Index) ठीक से समझा जा सकता है।
4.द्विपद प्रमेय में घातांक क्या है? (What is index in binomial theorem?)-
- द्विपद प्रमेय एक द्विपद की घातों को व्यक्त करने और मान ज्ञात करने का तरीका बताता है।इस प्रमेय के द्विपद में जब n एक ऋणात्मक पूर्णांक या एक भिन्न होता है, जहां, अन्यथा विस्तार संभव नहीं होगा।
5.आप एक द्विपद विस्तार का मान कैसे ज्ञात करते हैं? (How do you evaluate a binomial expansion?)-
- (1.)क्रमगुणित द्वारा व्यक्त पद का मान ज्ञात करें।
(2.)द्विपद गुणांक की गणना करें।
(3.)द्विपद प्रमेय का उपयोग करके द्विपद की घातों का विस्तार करें।
क्रमगुणित और द्विपद गुणांक - हम एक प्राकृतिक संख्या n के क्रमगुणित को परिभाषित करते हुए शुरू करते हैं,n! को निरूपित करते हैं ,n के समान या उससे कम सभी प्राकृतिक संख्याओं के गुणनफल के रूप में।
n! = n (n-1) (n-2) ⋯ 3⋅2⋅1
उदाहरण के लिए,
7! = 7⋅6⋅5⋅4⋅3⋅2⋅1=5,040
5!=5⋅4⋅3⋅2⋅1=120
3! =3⋅2⋅1 = 6
1! = 1
हम 1 के बराबर शून्य फैक्टरियल को परिभाषित करते हैं,
0! = 1
एक ऋणात्मक संख्या के फैक्टरियल को परिभाषित नहीं किया गया है। - द्विपद प्रमेय विस्तार पर विचार करें { (x+2) }^{ 5 } :
{ (x+2) }^{ 5 } = (x + 2) (x + 2) (x + 2) (x + 2) (x + 2) - एक को जल्दी से पता चलता है कि यह एक बहुत थकाऊ गणना है जिसमें वितरण गुणधर्म के कई अनुप्रयोग शामिल हैं।द्विपद प्रमेय प्रत्येक गुणनखंड को सीधे गुणा किए बिना, पदों को उठाए गए द्विपद को विस्तारित करने की एक विधि प्रदान करता है:
(x+y)^{ n }=(\begin{matrix} n \\ 0 \end{matrix}){ x }^{ n }{ y }^{ 0 }+(\begin{matrix} n \\ 1 \end{matrix}){ x }^{ n-1 }{ y }^{ 1 }+(\begin{matrix} n \\ 2 \end{matrix}){ x }^{ n-2 }{ y }^{ 2 }+........+(\begin{matrix} n \\ n-1 \end{matrix}){ x }^{ 1 }{ y }^{ n-1 }+(\begin{matrix} n \\ n \end{matrix}){ x }^{ 0 }{ y }^{ n } - द्विपद प्रमेय को अधिक संक्षेप में हम लिख सकते हैं,
(x+y)^{ n }=\overset { n }{ \underset { k=0 }{ \Sigma } } (\begin{matrix} n \\ k \end{matrix}){ x }^{ n-k }{ y }^{ k }
6.आप द्विपद प्रमेय कैसे करते हैं? (How do you do binomial theorem?)-
- द्विपद प्रमेय क्रिया में
आरंभ करने के लिए, आपको अपने द्विपद (ऊपर और हमारे सूत्र के x और y स्थान) से दो पदों की पहचान करने की आवश्यकता है और जिस घात (n) से आप द्विपद का विस्तार कर रहे हैं।उदाहरण के लिए, { (2x-3) }^{ 3 } (का विस्तार करने के लिए, दो पद 2x और -3 हैं और घात या n का मान 3 है।
7.परिमेय और अपरिमेय घातांकों के साथ द्विपद प्रमेय (Binomial Theorem with Rational and Irrational Indices)-
- एक द्विपद को एक अपरिमेय के साथ हल करने की विधि वही है जो एक द्विपद को हल करने के लिए परिमेय घातांक के साथ है।तो, हमारे पास एक अनंत श्रृंखला है,पदों के साथ,एक निश्चित बिंदु के बाद,धनात्मक और ऋणात्मक संख्याओं के बीच बारी-बारी से।
- उपर्युक्त उदाहरणों, सवालों को हल करके तथा प्रश्नों के उत्तर द्वारा किसी भी घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Any Index),ऋणात्मक घातांक के लिए द्विपद प्रमेय (Binomial Theorem for Negative Index), को ठीक प्रकार से समझा जा सकता है।
Also Read This Article:-Binomial Theorem
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |