Application of Heron Formula
1.हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula),हीरोन का सूत्र (Formula of Heron):
हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula) चतुर्भुजों के क्षेत्रफल ज्ञात करने में किया जाता है।अनेक बार खेत चतुर्भुजों के आकार के होते हैं।हमें चतुर्भुजाकार को त्रिभुजाकार भागों में विभाजित करना पड़ता है और फिर त्रिभुज के क्षेत्रफल के सूत्र का प्रयोग करके चतुर्भुज का क्षेत्रफल ज्ञात हो जाता है।
हीरोन के सूत्र (Formula of Heron) से:
त्रिभुज का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)}
जहाँ a,b और c त्रिभुज की भुजाएँ हैं तथा s=त्रिभुज का अर्धपरिमाप (Semi-perimeter)=\frac{a+b+c}{2}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Law of Exponents for Real Numbers
2.हीरोन के सूत्र का अनुप्रयोग के उदाहरण (Application of Heron Formula Examples):
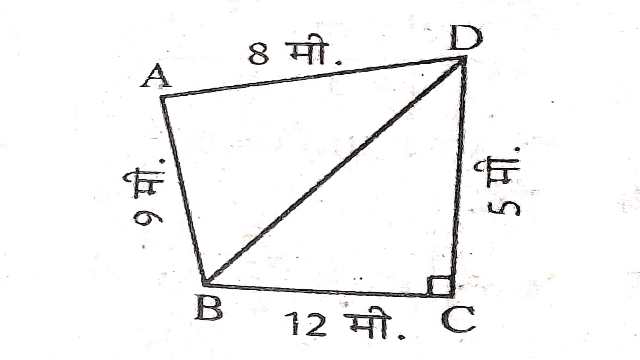
Example:1.एक पार्क ABCD के आकार का है जिसमें,AB=9 m,BC=12 m,CD=5 m और AD=8 m है।इस पार्क का कितना क्षेत्रफल है?
Solution:\triangle ABD का क्षेत्रफल के लिए:
पाइथागोरस प्रमेय द्वारा:BD^{2} =BC^{2}+C D^{2} \\ =(12)^{2}+(5)^{2} \\ =144+25 \\ =169 \\ \Rightarrow B D=\sqrt{169}
=13 मीटर
माना a=13 मीटर,b=9 मीटर,c=8 मीटर
S=\frac{a+b+c}{2}=\frac{13+9+8}{2}=\frac{30}{2}=15 मीटर
\triangle ABD का क्षेत्रफल (हीरोन के सूत्र से:)
=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{15(15-13)(15-9)(15-8)} \\ =\sqrt{15 \times 2 \times 6 \times 7} \\ =\sqrt{2 \times 2 \times 3 \times 3 \times 5 \times 7} \\ =2 \times 3 \sqrt{35} \\ =6 \sqrt{35} =6 × 5.916=35.496 वर्गमीटर
त्रिभुज BCD का क्षेत्रफल
आधार BC=12 मीटर,ऊँचाई=5 मीटर
त्रिभुज का क्षेत्रफल=\frac{1}{2} × आधार×ऊँचाई
=\frac{1}{2} ×12 ×5=30 वर्गमीटर
चतुर्भुज ABCD का क्षेत्रफल=\triangle ABD का क्षेत्रफल+\triangle CBD का क्षेत्रफल
=35.496+30=65.496 वर्गमीटर
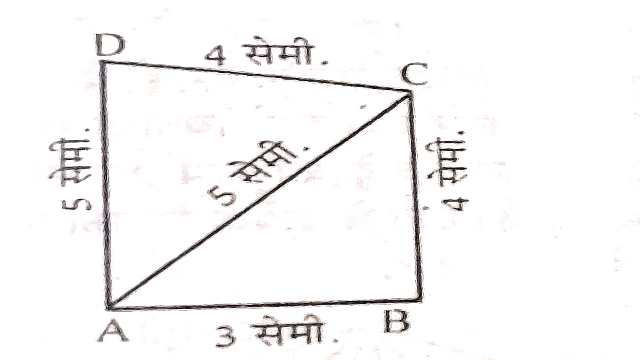
Example:2.एक चतुर्भुज का क्षेत्रफल ज्ञात कीजिये जिसमें AB=3 cm,BC=4 cm,CD=4 cm,DA=5 cm और AC=5 cm है।
Solution:\triangle ABC के लिए
S=\frac{a+b+c}{2}=\frac{3+4+5}{2}=\frac{12}{2}=6 सेमी
हीरोन के सूत्र (Formula of Heron) से:
\triangle ABC का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{6(6-3)(6-4)(6-5)} \\ =\sqrt{6 \times 3 \times 2 \times 1}
=6 वर्गसेमी
\triangle ACD के लिए
S=\frac{a+b+c}{2}=\frac{5+5+4}{2}=\frac{14}{2}=7 सेमी
\triangle ACD का क्षेत्रफल =\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{7(7-5)(7-5)(7-4)} \\ =\sqrt{7 \times 2 \times 2 \times 3} \\ =2 \sqrt{21} वर्गसेमी =2 × 4.583 =9.166 वर्गसेमी
अतः चतुर्भुज ABCD का क्षेत्रफल=\triangle ABC का क्षेत्रफल+\triangle ACD का क्षेत्रफल=6+9.166=15.166 वर्गसेमी
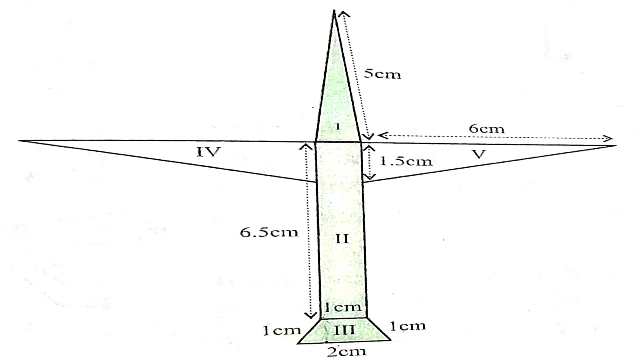
Example:3.राधा ने एक रंगीन कागज से एक हवाईजहाज का चित्र बनाया जैसाकि आकृति में दिखाया गया है।प्रयोग किए गए कागज का कुल क्षेत्रफल ज्ञात कीजिए।
Solution:त्रिभुज के क्षेत्रफल के लिए (भाग I):
a=5,b=5,c=1
S=\frac{5+5+1}{2}=\frac{11}{2}=5.5
हीरोन का सूत्र (Formula of Heron) से:
त्रिभुज का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{5.5(5.5-5)(5.5-5)(5.5-1)} \\ =\sqrt{5.5 \times 0.5 \times 0.5 \times 4.5} \\=0.5 \sqrt{5.5 \times 4.5} \\ =0.5 \times \sqrt{24.75}=0.5 × 4.975 =2.4875 वर्गसेमी
आयत का क्षेत्रफल (भाग II)=लम्बाई × चौड़ाई
=6.5 × 1
=6.5 वर्गसेमी
समलम्ब चतुर्भुज के क्षेत्रफल के लिए (भाग III):
समान्तर भुजाओं के बीच दूरी=\sqrt{(1)^{2}-(0.5)^{2}} \\ =\sqrt{1-0.25} \\ =\sqrt{.75} \\ =\sqrt{\frac{75}{100}} \\ = \frac{5}{10} \sqrt{3} =0.5 × 1.732 =0.866 वर्गसेमी
समलम्ब चतुर्भुज का क्षेत्रफल=\frac{1}{2} × (समान्तर भुजाओं का योग)×उनके बीच दूरी
=\frac{1}{2} ×(2+1)×0.866
=1.299 वर्गसेमी
त्रिभुज का क्षेत्रफल (भाग IV व V):
=\frac{1}{2} × आधार × ऊँचाई
=\frac{1}{2} ×1.5 × 6
=4.5 वर्गसेमी
दोनों भागों का कुल क्षेत्रफल=2×4.5
=9 वर्गसेमी
अतः कागज का कुल क्षेत्रफल = 2.4875+6.5+1.299+9=19.2865 वर्गसेमी \approx 19.3 वर्गसेमी
Example:4.एक त्रिभुज और एक समान्तर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है।यदि त्रिभुज की भुजाएँ 26 cm,28 cm और 30 cm हैं तथा समान्तर चतुर्भुज 28 cm के आधार पर स्थित है तो उसकी संगत ऊँचाई ज्ञात कीजिए।
Solution:त्रिभुज के लिए:
a=26 cm,b=28 cm,c=30 cm
S=\frac{a+b+c}{2}=\frac{26+28+30}{2}=\frac{84}{2}=42
हीरोन का सूत्र (Formula of Heron) से:
=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{42(42-26)(42-28)(42-30)} \\ =\sqrt{42 \times 16 \times 14 \times 12} \\ =\sqrt{2 \times 3 \times 7 \times 2 \times 2 \times 2 \times 2 \times 2 \times 7 \times 2 \times 2 \times 3} \\ =\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 7 \times 7} \\ =2 \times 2 \times 2 \times 2 \times 3 \times 7=336 cm^{2}
त्रिभुज का क्षेत्रफल
समान्तर चतुर्भुज का क्षेत्रफल=336
28 × ऊँचाई=336
=\frac{336}{28}=12 सेमी
Example:5.एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है।यदि इस समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48 m है तो प्रत्येक गाय को चरने के लिए इस घास के क्षेत्रफल का कितना क्षेत्रफल प्राप्त होगा?
Solution:समचतुर्भुजाकार घास के खेत का क्षेत्रफल=2 × त्रिभुज का क्षेत्रफल
त्रिभुज के क्षेत्रफल के लिए:
a=30,b=30,c=48
S=\frac{a+b+c}{2}=\frac{30+30+48}{2}=54
हीरोन का सूत्र (Formula of Heron) से:
=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{54(54-30)(54-30)(54-48)} \\ =\sqrt{54 \times 24 \times 24 \times 6} \\ =\sqrt{2 \times 3 \times 3 \times 3 \times 2 \times 2 \times 2 \times 3 \times 2 \times 2 \times 2 \times 3 \times 2 \times 3} \\ =\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3}
त्रिभुज का क्षेत्रफल=2 × 2 ×2×2×3×3×3=432 वर्गमीटर
समचतुर्भुजाकार खेत का क्षेत्रफल=432 × 2= 864 वर्गमीटर
प्रत्येक गाय के लिए घास का क्षेत्रफल=\frac{864}{18}=48 वर्गमीटर
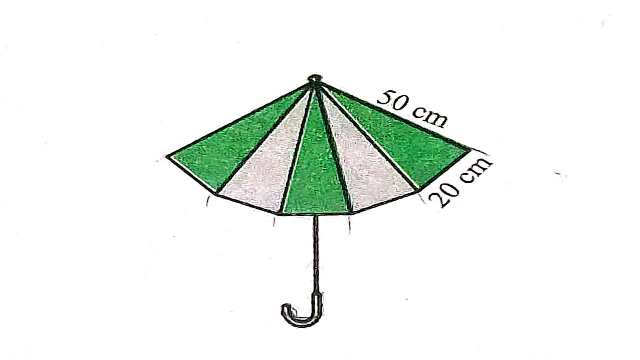
Example:6.दो विभिन्न रंगों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है (देखिए आकृति)।प्रत्येक टुकड़े के माप 20 cm,50 cm और 50 cm है।छाते में प्रत्येक रंग का कितना कपड़ा लगा है?
Solution:एक त्रिभुजाकार टुकड़े के क्षेत्रफल के लिए:
a=20 cm,b=50 cm,c=50 cm
S=\frac{a+b+c}{2}=\frac{20+50+50}{2}=\frac{120}{2}=60 cm
हीरोन का सूत्र (Formula of Heron) से:
त्रिभुज का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)} \\=\sqrt{60(60-20)(60-50)(60-50)} \\ =\sqrt{60 \times 40 \times 10 \times 10} \\ =\sqrt{20 \times 3 \times 20 \times 2 \times 10 \times 10} \\ =20 \times 10 \sqrt{6} \\ =200 \sqrt{6} वर्गसेमी
5 त्रिभुजाकार टुकड़ों में लगा कपड़ा=200 \sqrt{6} \times 5
=1000 \sqrt{6} वर्गसेमी
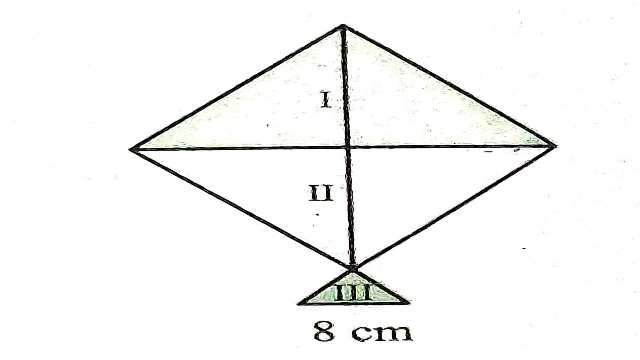
Example:7.एक पतंग तीन भिन्न-भिन्न शेडों (Shades) के कागजों से बनी है।इन्हें आकृति I,II और III से दर्शाया गया है।पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm,6 cm और 8 cm भुजाओं का एक समद्विबाहु त्रिभुज है।ज्ञात कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है।
Solution:समद्विबाहु त्रिभुज का क्षेत्रफल (भाग I)=\frac{1}{2}×आधार × ऊँचाई
=\frac{1}{2}×32×16
=256 वर्गसेमी
इसी प्रकार समद्विबाहु त्रिभुज का क्षेत्रफल (भाग II)=256 वर्गसेमी
समद्विबाहु त्रिभुज के क्षेत्रफल (भाग III) के लिए:
a=6,b=6,c=8 सेमी
S=\frac{a+b+c}{2}=\frac{6+6+8}{2}=\frac{20}{2}=10 सेमी
हीरोन का सूत्र (Formula of Heron) से:
त्रिभुज का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{10(10-6)(10-6)(10-8)} \\=\sqrt{10 \times 4 \times 4 \times 2 }\\=\sqrt{2 \times 5 \times 2 \times 2 \times 2 \times 2 \times 2 } \\=2 \times 2 \times 2 \sqrt{5} =8 \sqrt{5} वर्गसेमी
भाग I में प्रयुक्त कागज=256 वर्गसेमी, भाग II में प्रयुक्त कागज=256 वर्गसेमी, भाग III में प्रयुक्त कागज=8 \sqrt{5} वर्गसेमी
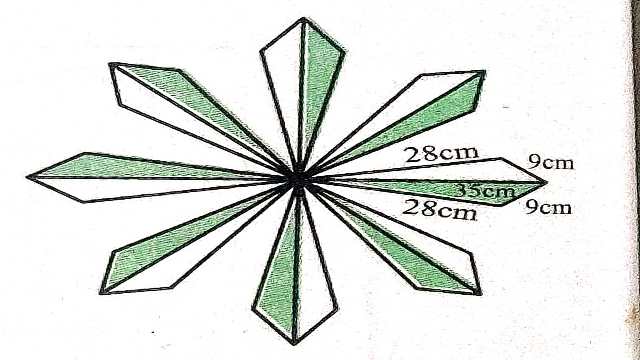
Example:8.फर्श पर एक फूलों का डिजाइन 16 त्रिभुजाकार टाइलों से बनाया गया है जिनमें से प्रत्येक की भुजाएँ 9 cm,28 cm और 35 cm है (देखिए आकृति)।इन टाइलों को 50 पैसे प्रति वर्गसेमी की दर से पालिश कराने का व्यय ज्ञात कीजिए।
Solution:एक टाइल के क्षेत्रफल के लिए:
a=9 cm,b=28 cm,c=35 cm
S=\frac{a+b+c}{2}=\frac{9+28+35}{2}=\frac{72}{2}=36 cm
हीरोन का सूत्र (Formula of Heron) से:
त्रिभुज का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)} \\=\sqrt{36(36-9)(36-28)(36-35)} \\ =\sqrt{36 \times 27 \times 8 \times 1} \\ =6 \times 3 \times 2 \times \sqrt{6}=36 \sqrt{6} वर्गसेमी
=36×2.449
=88.164 वर्गसेमी
16 टाइलों का क्षेत्रफल=88.164 × 16
=1410.624 वर्गसेमी
पालिश कराने का व्यय=1410.624 × .5
=705.312 \approx 705.31 Rs.
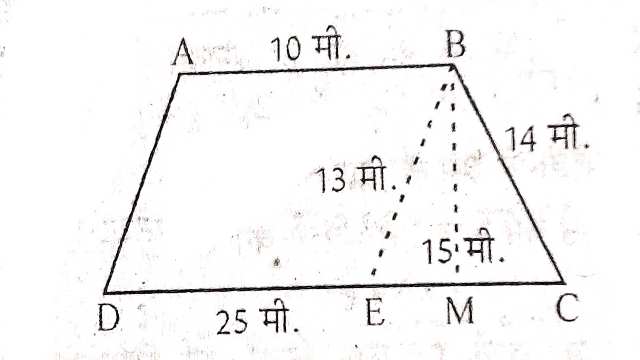
Example:9.एक खेत समलम्ब के आकार का है जिसकी समान्तर भुजाएँ 25 m और 10 m हैं।इसकी असमान्तर भुजाएँ 14 m और 13 m हैं।इस खेत का क्षेत्रफल ज्ञात कीजिए।
Solution:त्रिभुज BEC के क्षेत्रफल के लिए:
a=13 मीटर,b=14 मीटर,c=15 मीटर
S=\frac{a+b+c}{2}=\frac{13+14+15}{2}=\frac{42}{2}=21 मीटर
हीरोन का सूत्र (Formula of Heron) से:
\triangle BEC का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)} \\=\sqrt{21(21-13)(21-14)(21-15)} \\ =\sqrt{21 \times 8 \times 7 \times 6} \\=\sqrt{3 \times 7 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3}\\ =2 \times 2 \times 3 \times 7
=84 वर्गमीटर
तथा \triangle BEC का क्षेत्रफल=\frac{1}{2} × EC ×BM
\Rightarrow 84=\frac{1}{2} \times 15 \times BM \\ \Rightarrow BM=\frac{84 \times 2}{15} \\ \Rightarrow BM=\frac{56}{5} मीटर
समान्तर चतुर्भुज ABED का क्षेत्रफल=आधार × ऊँचाई
=DE × BM =10 \times \frac{56}{5}
=112 वर्गमीटर
अतः समलम्ब चतुर्भुज ABCD का क्षेत्रफल= समान्तर चतुर्भुज ABED का क्षेत्रफल + \triangle BECका क्षेत्रफल
=112+84=196 वर्गमीटर
उपर्युक्त उदाहरणों के द्वारा हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula),हीरोन का सूत्र (Formula of Heron) को समझ सकते हैं।
3.हीरोन के सूत्र का अनुप्रयोग की समस्याएँ (Application of Heron Formula Problems):
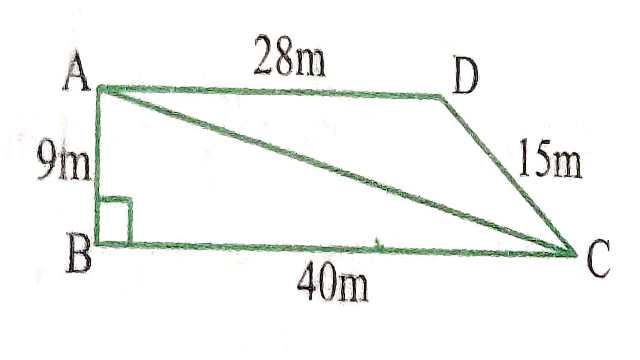
(1.)किसी समूह के विद्यार्थियों ने सफाई अभियान के लिए एक रैली निकाली।उन्होंने दो समूहों में विभिन्न गलियों में चलकर मार्च किया।एक समूह ने गलियों AB,BC और CA में मार्च किया तथा अन्य समूह ने गलियों AC,CD और DA में मार्च किया (देखिए आकृति)।फिर उन्होंने इन गलियों द्वारा घेरे गए भागों को साफ किया।यदि AB=9 m,BC=40 m,CD=15 m,DA=28 और \angle B=90^{\circ} है तो किस समूह ने अधिक सफाई की और कितनी अधिक?विद्यार्थियों द्वारा सफाई किया गया कुल क्षेत्रफल भी ज्ञात कीजिए (यह मानकर चलिए कि गलियों की चौड़ाई को छोड़ा जा सकता है।)
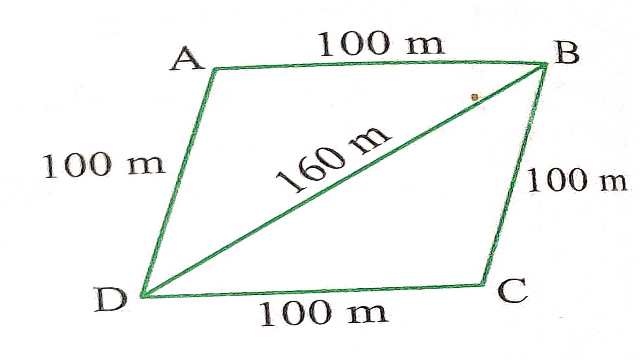
(2.)सानया के पास एक खेत है जो एक समचतुर्भुज के आकार का है (देखिए आकृति)।वह अपनी एक पुत्री और एक पुत्र से यह चाहती थी कि वे इस खेत पर काम करके अलग-अलग फसलों (या उपजों) का उत्पादन करें।उसने इस खेत को दो बराबर भागों में विभाजित कर दिया।यदि इस खेत का परिमाप 400 m है और एक विकर्ण 160 m है तो प्रत्येक को खेती के लिए कितना क्षेत्रफल प्राप्त होगा?
उत्तर (Answers):(1.)180,126,सफाई का कुल क्षेत्रफल=306 वर्गमीटर
(2.)4800 वर्गमीटर
उपर्युक्त सवालों को हल करने पर हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula),हीरोन का सूत्र (Formula of Heron) को ठीक से समझ सकते हैं।
Also Read This Article:-Rationalisation of Denominator
4.हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula),हीरोन का सूत्र (Formula of Heron) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.हीरोन का सूत्र लिखो।(Write the formula of Heron):
उत्तर:यदि त्रिभुज की भुजाएँ a,b और c हों तो हीरोन के सूत्र द्वारा त्रिभुज का क्षेत्रफल=\sqrt{S(S-a)(S-b)(S-c)}
जहाँ \frac{a+b+c}{2}
प्रश्न:2.यदि चतुर्भुज का विकर्ण और भुजाएँ ज्ञात हों तो क्षेत्रफल कैसे ज्ञात करें? (Quadrilateral are known then how to find the area?):
उत्तर:एक चतुर्भुज जिसकी भुजाएँ तथा एक विकर्ण दिए हों तो उसका क्षेत्रफल उसे दो त्रिभुजों में विभाजित करके और फिर हीरोन का सूत्र प्रयोग करके ज्ञात किया जा सकता है।
प्रश्न:3.हीरोन कौन था? (Who was Heron?):
उत्तर:हीरोन का जन्म संभवतः मिस्र में अलेक्जेंड्रिया नामक स्थान पर हुआ।उन्होंने अनुप्रायोगिक गणित (Applied Mathematics) पर कार्य किया।उनका गणितीय और भौतिकीय विषयों पर कार्य इतना अधिक और विभिन्न प्रकार का था कि उन्हें इन क्षेत्रों का एक विश्वकोश सम्बन्धी (Encyclopedia) लेखक समझा जाता था।उनका ज्यामितीय कार्य मुख्यतः मेन्सुरेशन (क्षेत्रमिति) की समस्याओं से सम्बन्धित पुस्तक I में वर्गों,आयतों,त्रिभुजों,समलम्बों,अनेक प्रकार के विशिष्ट चतुर्भुजों,समबहुभुजों,वृत्तों के क्षेत्रफलों,बेलनों,शंकुओं,गोलों इत्यादि के पृष्ठीय क्षेत्रफलों का वर्णन है।इसी पुस्तक में हीरोन ने त्रिभुज की तीनों भुजाओं के पदों में उसके क्षेत्रफल का प्रसिद्ध (या सुपरिचित) सूत्र प्रतिपादित किया गया है।
उपर्युक्त प्रश्नों के उत्तर द्वारा हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula),हीरोन का सूत्र (Formula of Heron) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
Application of Heron Formula
हीरोन के सूत्र का अनुप्रयोग
(Application of Heron Formula)
Application of Heron Formula
हीरोन के सूत्र का अनुप्रयोग (Application of Heron Formula) चतुर्भुजों के क्षेत्रफल ज्ञात करने में किया जाता है।
अनेक बार खेत चतुर्भुजों के आकार के होते हैं।हमें चतुर्भुजाकार को त्रिभुजाकार भागों में विभाजित करना पड़ता है
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
