Theorem of Area of Parallelogram
1.समांतर चतुर्भुज के क्षेत्रफल का प्रमेय (Theorem of Area of Parallelogram),समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल प्रमेयों के प्रमाण कक्षा 9 (Areas of Parallelograms and Triangles Class 9 Theorems Proofs):
समांतर चतुर्भुज के क्षेत्रफल का प्रमेय (Theorem of Area of Parallelogram):एक सरल बंद समांतर चतुर्भुज की आकृति द्वारा किसी तल पर घेरा हुआ भाग उस आकृति (समांतर चतुर्भुज का) तलीय क्षेत्र कहलाता है और इस क्षेत्र का परिमाण या माप उस आकृति का क्षेत्रफल (Area) कहलाता है।इस परिमाण या माप को सदैव किसी मात्रक की सहायता से व्यक्त किया जाता है।
यदि दो आकृतियां आकार एवं माप में समान हों तो वे सर्वांगसम आकृतियां हैं।यदि उन्हें काटकर किसी तल पर रखें तो उस तल पर दोनों ही आकृतियों का तलीय क्षेत्रफल समान आता है।अर्थात् दो सर्वांगसम आकृतियां क्षेत्रफल में समान होती है।परंतु क्षेत्रफल में समान आकृतियां सर्वांगसम भी हो यह आवश्यक नहीं है।
प्रमेय (Theorem):1.एक ही आधार और एक ही समांतर रेखाओं के बीच के समांतर चतुर्भुजों के क्षेत्रफल बराबर होते हैं।
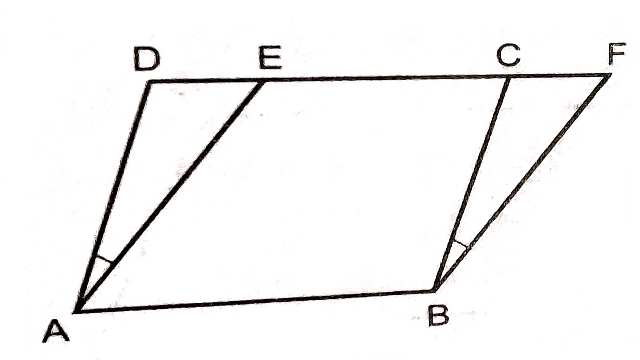
दिया है (Given):दो समांतर चतुर्भुज ABCD और ABFE जिनका आधार AB है,जो समांतर रेखाओं AB और DF के मध्य स्थित है।
सिद्ध करना है (To Prove):समांतर चतुर्भुज ABCD का क्षेत्रफल=समांतर चतुर्भुज ABFE का क्षेत्रफल
उपपत्ति (Proof): \triangle ADE और \triangle BCF में
AB=BF (समान्तर चतुर्भुज ABFE की सम्मुख भुजाएं)
\angle DAE=\angle CBF(संगत कोण)
AD=BC (समान्तर चतुर्भुज ABCD की सम्मुख भुजाएं)
अर्थात् भुजा-कोण-भुजा सर्वांगसमता से (By SAS Congruence Property)
\triangle ADE \cong \triangle BCF
अतः क्षेत्रफल (\triangle ADE )=क्षेत्रफल (\triangle BCF)
क्षेत्रफल दोनों पक्षों में क्षेत्रफल (ABCE) जोड़ने पर-
क्षेत्रफल (\triangle ADE )+ क्षेत्रफल(ABCE)=क्षेत्रफल (\triangle BCF)+ क्षेत्रफल (ABCE)
क्षेत्रफल (ABCD)=क्षेत्रफल (ABFE)
प्रमेय (Theorem):2.एक समांतर चतुर्भुज और एक आयत जो एक ही आधार तथा दो समांतर रेखाओं के बीच स्थित हों तो उनके क्षेत्रफल समान होते हैं तथा समांतर चतुर्भुज का क्षेत्रफल आधार × दोनों समांतर रेखाओं के मध्य दूरी के गुणन के बराबर होता है।
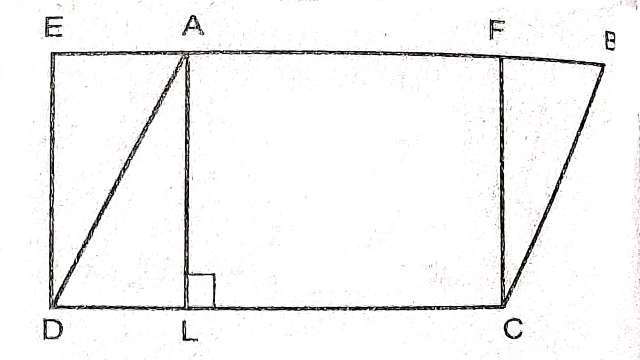
दिया है (Given):चित्र में ABCD एक समांतर चतुर्भुज और EFCD एक आयत है।साथ ही है।
सिद्ध करना है (To Prove):(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL
उपपत्ति (Proof):(i)चूंकि आयत एक समांतर चतुर्भुज भी होता है।
अतः ar(ABCD)=ar(EFCD) ……..(1)
[एक ही आधार और एक ही समांतर रेखाओं के बीच के समांतर चतुर्भुजों का क्षेत्रफल बराबर होता है]
(ii)आयत का क्षेत्रफल=लंबाई × चौड़ाई
अतः ar(EFCD)=DC×FC
इसलिए ar(ABCD)=DC×FC [(1) से] …..(2)
AL \perp DC दिया हुआ है
इस प्रकार AFCL भी एक आयत है।
AL=FC ………(3)
ar(ABCD)=DC×AL [(2) एवं (3) से]
प्रमेय (Theorem):3.एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समान्तर रेखा युग्म के साथ स्थित हो तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
दिया है (Given):\triangle ABP और समान्तर चतुर्भुज ABCD एक ही आधार AB पर एवं AB \parallel PC के मध्य बने है।
सिद्ध करना है (To Prove):ar(PAB)=\frac{1}{2} ar(ABCD)
रचना (Construction):BQ रेखा AB के समांतर खींची।
उत्पत्ति (Proof): AB \parallel CD (दिया हुआ है)
अतः AB \parallel PQ
तथा AB \parallel BQ (रचना से)
अतः ABQP एक समांतर चतुर्भुज है।
ar(ABCD)=ar(ABQP)
[एक ही आधार और एक ही समांतर रेखाओं के बीच के समांतर चतुर्भुजों का क्षेत्रफल बराबर होता है।]
तथा \triangle ABP \cong \triangle QPB(समांतर चतुर्भुज का एक विकर्ण समान्तर चतुर्भुज को दो सर्वांगसम त्रिभुज में विभाजित करता है)
अतः ar(ABP)=ar(QPB)=\frac{1}{2} ar(ABQP) \\ \Rightarrow ar(ABP)=\frac{1}{2} ar(ABCD)
प्रमेय (Theorem):4.त्रिभुज का क्षेत्रफल (Area of Triangle) =\frac{1}{2} \text{ ×आधार×ऊंचाई } होता है।
यदि DL \perp AB है तो
ar(ABCD)=AB×DL
परन्तु ar(PAB)=\frac{1}{2} ar(ABCD)
अतः ar(PAB)=\frac{1}{2} AB \times DL
अर्थात् त्रिभुज का क्षेत्रफल=\frac{1}{2} \text{ ×आधार×ऊंचाई }
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Aslo Read This Article:- Angles of a Triangle
2.समांतर चतुर्भुज के क्षेत्रफल का प्रमेय के उदाहरण (Theorem of Area of Parallelogram Examples):
Example:1.चित्र में ABCD एक समान्तर चतुर्भुज है, AE \perp DC और CF \perp AD है।यदि AB=16cm,AE=8cm और CF=10cm है तो AD ज्ञात कीजिए।
Solution:समान्तर चतुर्भुज ABCD का क्षेत्रफल=आधार×ऊंचाई
AB×AE=AD×CF \\ \Rightarrow 16×8=AD×10 \\ \Rightarrow AD=\frac{16 \times 8}{10} \\ \Rightarrow AD=\frac{128}{10} \\ \Rightarrow AD=12.8 cm
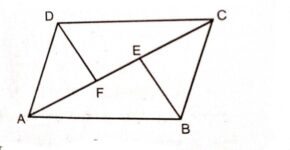
Example:2.P और Q क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं।दर्शाइए कि ar(APB)=ar(BQC) है।
Solution: दिया है (Given):ABCD एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):ar(APB)=ar(BQC)
उपपत्ति:\triangle APB तथा समान्तर चतुर्भुज ABCD एक ही आधार AB तथा एक ही समान्तर भुजाओं AB व CD के बीच स्थित हैं।
\therefore ar(APB)=\frac{1}{2} ar(ABCD) \cdots(1)
\triangle BQC और समान्तर चतुर्भुज ABCD एक ही आधार BC तथा एक ही समान्तर रेखाओं BC व CD के मध्य स्थित हैं।
\therefore ar(BQC)=\frac{1}{2} ar(ABCD) \cdots(2)
समीकरण (1) व (2) से-
ar(APB)=ar(BQC)
Example:3.चित्र में P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिन्दु है।दर्शाइए कि
(i)ar(APB)+ar(PCD)=\frac{1}{2} ar(ABCD) \\ (ii)ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
Solution:(i) \triangle APB और समान्तर चतुर्भुज ABFE एक ही आधार AB पर और एक ही समान्तर रेखाओं AB और DC के मध्य स्थित हैं।
\therefore ar(APB)=\frac{1}{2} ar(ABFE) \cdots(1)
इसी प्रकार ar(PCD)=\frac{1}{2} ar(FECD) \cdots(1)
समीकरण (1) व (2) को जोड़ने पर-
ar(APB)+ar(PCD)=\frac{1}{2}[ar(ABFE)+ar(EFCD)] \\ \Rightarrow ar(APB)+ar(PCD)=\frac{1}{2} ar(ABCD) \cdots(3)
(ii)\triangle APD और समान्तर चतुर्भुज AGHD एक ही आधार AD पर और एक ही समान्तर रेखाओं AD और HG के मध्य स्थित हैं।
ar(APD)=\frac{1}{2} ar(AGHD) \cdots(4)
इसी प्रकार ar(PCD)=\frac{1}{2} ar(GBCH) \cdots(5)
समीकरण (4) व (5) को जोड़ने पर-
ar(APD)+ar(PCD)=\frac{1}{2} [ar(AGHD)+ ar(GBCH)] \\ \Rightarrow ar(APD)+ar(PCD)=\frac{1}{2} ar(ABCD) \cdots(6)
समीकरण (5) व (6) को जोड़ने पर-
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)[/katex]
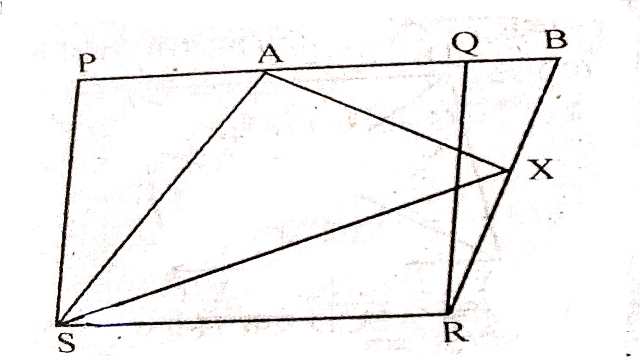
Example:4.चित्र में PQRS और ABRS समान्तर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिन्दु है।दर्शाइए कि
(i)ar(PARS)=ar(ABRS) \\ (ii)ar(AXS)=\frac{1}{2} ar(PQRS)
Solution: दिया है (Given):दो समान्तर चतुर्भुज PQRS और ABRS तथा भुजा BR पर एक बिन्दु X स्थित है।
सिद्ध करना है (To Prove): (i)ar(PQRS)=ar(ABRS) \\ (ii)ar(AXS)=\frac{1}{2} ar(PQRS)
उपपत्ति (Proof):(i)समान्तर चतुर्भुज PQRS और ABRS एक ही आधार SR और एक ही समान्तर भुजाओं SR और PB के बीच स्थित हैं।
\therefore ar(PQRS)=ar(ABRS) …….(1)
(ii) \triangle AXS और समान्तर चतुर्भुज ABRS एक ही आधार AS और एक ही समान्तर रेखाओं AS और RB के बीच स्थित हैं।
ar(AXS)=\frac{1}{2} ar(ABRS) \cdots(2)
समीकरण (1) व (2) से-
ar(AXS)=\frac{1}{2} ar(PQRS)
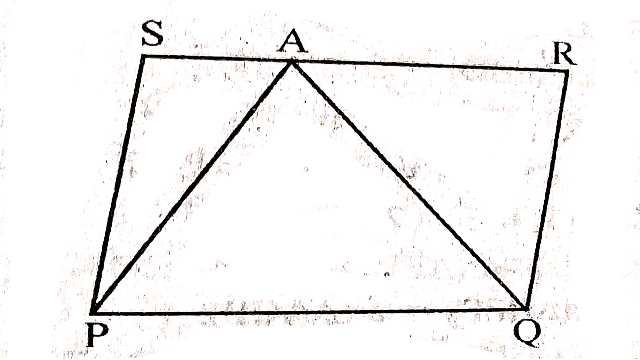
Example:5.एक किसान के पास समान्तर चतुर्भुज PQRS के रूप का खेत है। उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया।खेत कितने भागों में विभाजित हो गया?इन भागों के आकार क्या हैं?वह किसान खेत में गेहूं और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है।वह ऐसा कैसे करे?
Solution:एक समान्तर चतुर्भुज PQRS भुजा SR पर एक बिन्दु A स्थित है।A को P और Q से मिलाया गया है। क्षेत्र को तीन भागों (i) \triangle ASP \quad (ii)\triangle APQ \quad (iii) \triangle AQR में बांटा गया है।सभी भाग त्रिभुज है।
\triangle APQ और समान्तर चतुर्भुज PQRS एक ही आधार PQ और एक ही समान्तर रेखाओं के बीच स्थित हैं।
ar(APQ)=\frac{1}{2} ar(PQRS) \cdots(1) \\ ar(ASP)+ar(APQ)+ar(AQR)=ar(PQRS) \\ \Rightarrow ar(ASP)+\frac{1}{2} ar(PQRS)+ar(AQR)=ar(PQRS) \\ \Rightarrow ar(ASP)+ar(AQR)=\frac{1}{2} ar(PQRS) \cdots(2)
समीकरण (1) व (2) से-
ar(APQ)=ar(ASP)+ar(AQR)
अतः किसान को APQ में गेहूं और अन्य दो त्रिभुजों में दालें बोनी चाहिए।
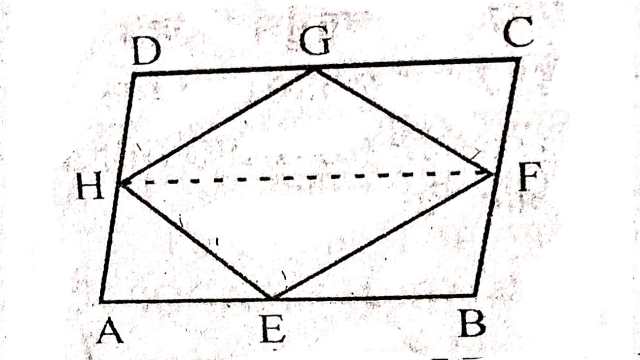
Example:6.यदि E,F,G तथा H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हैं तो दर्शाइए कि ar(EFGH)=\frac{1}{2} ar(ABCD) है।
Solution: दिया है (Given):ABCD एक समान्तर चतुर्भुज है तथा E,F,G,H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य बिन्दु हैं।
सिद्ध करना है (To Prove):ar(EFGH)=\frac{1}{2} ar(ABCD)
उपपत्ति (Proof): \triangle HGF और समान्तर चतुर्भुज HDCF एक ही आधार HF और एक ही समान्तर रेखाओं HF और DC के मध्य स्थित हैं।
ar(HGF)=\frac{1}{2} ar(HDCF) \cdots(1)
इसी प्रकार \triangle HEF और समान्तर चतुर्भुज ABFH एक ही आधार HF और एक ही समान्तर रेखाओं HF और AB के मध्य स्थित हैं।
ar(HEF)=\frac{1}{2} ar(ABFH) \cdots(2)
समीकरण (1) व (2) को जोड़ने पर-
ar(HGF)+ar(HEF)=\frac{1}{2} [ar(HDCF)+ar(ABFH)] \\ \Rightarrow ar(EFGH)=\frac{1}{2} ar(ABCD)
उपर्युक्त उदाहरणों के द्वारा समांतर चतुर्भुज के क्षेत्रफल का प्रमेय (Theorem of Area of Parallelogram) को समझ सकते हैं।
3.समांतर चतुर्भुज के क्षेत्रफल का प्रमेय की समस्याएं (Theorem of Area of Parallelogram Problems):
(1.)दो \triangle ABC और \triangle ABD एक ही आधार AB पर इस प्रकार स्थित हैं कि बिन्दु C तथा D आधार AB के एक ही ओर स्थित नहीं है।यदि रेखा CD भुजा AB द्वारा समद्विभाजित होती है तो सिद्ध कीजिए कि दोनों त्रिभुज क्षेत्रफल में समान है।
(2.) \triangle ABC में \angle B=90^{\circ} ;AB=4 सेमी और BC=3 सेमी हो तो कर्ण AC ज्ञात कीजिए।
(3.)एक सीढ़ी के नीचे का सिरा दीवार से 0.9 मीटर की
दूरी पर रखते हुए सीढ़ी दीवार के सहारे रखी हुई है।सीढ़ी का ऊपरी सिरा दीवार पर 4 मीटर ऊंचाई तक पहुंच जाता है।सीढ़ी की लम्बाई ज्ञात करो।
(4.)एक मनुष्य एक स्थान से प्रथम दक्षिण की ओर 34 मीटर चला,वहां से 48 मीटर पश्चिम की ओर,अन्य में 20 मीटर उत्तर की ओर गया।बताइए चलने के स्थान से उस स्थान की सीधी दूरी कितनी है।
उत्तर (Answers):(2.)5 सेमी
(3.)4.1 सेमी
(4.)50 सेमी
उपर्युक्त सवालों को हल करने पर समांतर चतुर्भुज के क्षेत्रफल का प्रमेय (Theorem of Area of Parallelogram) को ठीक से समझ सकते हैं।
Aslo Read This Article:-Mid Point Theorem
4.समांतर चतुर्भुज के क्षेत्रफल का प्रमेय (Theorem of Area of Parallelogram) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.समांतर चतुर्भुज का प्रमेय क्या है? (What is the theorem of parallelograms?):
उत्तर:एक समांतर चतुर्भुज में,विपरीत भुजाएँ समान लंबाई की होती हैं।प्रमेय 2: यदि एक चतुर्भुज में विपरीत भुजाएँ समान लंबाई की हों, तो आकृति एक समांतर चतुर्भुज होती है।प्रमेय 3: एक चतुर्भुज एक समांतर चतुर्भुज होता है यदि और केवल यदि विकर्ण एक दूसरे को समद्विभाजित करते हैं।
प्रश्न:2.समांतर चतुर्भुज विकर्ण प्रमेय क्या है? (What is the parallelogram diagonals Theorem?):
उत्तर:एक समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं। उपपत्ति: ABCD दिया है, मान लीजिए कि विकर्ण AC और BD, E पर प्रतिच्छेद करते हैं, हमें सिद्ध करना होगा कि AE = CE और BE = DE विलोम भी सत्य है: यदि किसी चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं,तो चतुर्भुज एक समांतर चतुर्भुज होता है।
प्रश्न:3.समांतर चतुर्भुज का क्षेत्रफल ज्ञात करने का सूत्र क्या है? (What is the formula for finding the area of a parallelogram?):
उत्तर:समांतर चतुर्भुज का क्षेत्रफल A = b×h=आधार×ऊंचाई क्यों है,इसके लिए अंतर्ज्ञान।एक समांतर चतुर्भुज के क्षेत्रफल का सूत्र आधार गुणा ऊँचाई है,ठीक वैसे ही जैसे किसी आयत के क्षेत्रफल का सूत्र।
प्रश्न:4.आप एक समद्विभाजक समांतर चतुर्भुज को कैसे हल करते हैं? (How do you solve a bisect parallelogram?):
उत्तर:ABCD एक समांतर चतुर्भुज है,विकर्ण AC और BD,O पर प्रतिच्छेद करते हैं।
त्रिभुज \triangle AOD और \triangle COB में,
\angle DAO=\angle BCO (alternate interior angles)
AD = CB.
\angle ADO =\angle CBO (alternate interior angles)
\triangle AOD \cong \triangle COB (By ASA Congruence Property)
इसलिए, AO = CO और OD = OB (c.p.c.t)
इस प्रकार, एक समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
प्रश्न:5.क्या समांतर चतुर्भुज में विकर्ण बराबर होते हैं? (Are diagonals equal in a parallelogram?):
उत्तर:समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।एक समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
प्रश्न:6.आप समांतर चतुर्भुज के विकर्ण कैसे ज्ञात करते हैं? (How do you find the diagonals of a parallelogram?):
उत्तर:एक समांतर चतुर्भुज में,विकर्ण एक दूसरे को समद्विभाजित करते हैं,इसलिए आप लेबल वाले खंडों को एक दूसरे के बराबर सेट कर सकते हैं और फिर के लिए हल कर सकते हैं।x + 14 = 5x – 10 ,24 = 4x,6 = x.यदि , तो आप कुल 40 प्राप्त करने के लिए प्रत्येक लेबल वाले खंड x में 6 स्थानापन्न करते हैं।
प्रश्न:7.क्या एक समांतर चतुर्भुज 90 डिग्री पर समद्विभाजित करता है? (Does a parallelogram bisect at 90 degrees?):
उत्तर:सभी समान्तर चतुर्भुजों के विकर्ण परस्पर समकोण पर नहीं काटते हैं।केवल वर्ग और समचतुर्भुज के विकर्ण परस्पर समकोण पर काटते हैं।
प्रश्न:8.क्या सभी वर्ग रॉम्बी हैं? (Are all squares Rhombi?)
उत्तर:सभी वर्ग समचतुर्भुज हैं,लेकिन सभी समचतुर्भुज वर्ग नहीं हैं।समचतुर्भुज के विपरीत आंतरिक कोण सर्वांगसम होते हैं।समचतुर्भुज के विकर्ण हमेशा एक दूसरे को समकोण पर समद्विभाजित करते हैं।
प्रश्न:9.क्या समांतर चतुर्भुज के विकर्ण कोणों को समद्विभाजित करते हैं? (Do diagonals of parallelogram bisect angles?):
उत्तर:समांतर चतुर्भुज एक चतुर्भुज होता है जिसकी विपरीत भुजाएँ समानांतर होती हैं। समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।एक समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
प्रश्न:10.समांतर चतुर्भुज किस आकार का होता है? (What shape is a parallelogram?):
उत्तर:एक समांतर चतुर्भुज एक चतुर्भुज है जिसमें समानांतर पक्षों के 2 जोड़े होते हैं।इन आकृतियों में एक ही रंग की भुजाएँ एक-दूसरे के समानांतर हैं।समान लंबाई की चार भुजाओं वाली एक आकृति।आकृति में समानांतर भुजाओं के दो सेट हैं और इनमें दो आसन्न भुजाएं के बीच कोण समकोण नहीं है।
प्रश्न:11.आरेख के साथ समांतर चतुर्भुज क्या है? (What is parallelogram with diagram?):
उत्तर:यूक्लिडियन ज्यामिति में एक समांतर चतुर्भुज एक सरल (गैर-स्व-प्रतिच्छेदन) चतुर्भुज होता है जिसमें समानांतर पक्षों के दो जोड़े होते हैं।एक समान्तर चतुर्भुज की सम्मुख भुजाएँ समान लंबाई की होती हैं और समांतर चतुर्भुज के सम्मुख कोण समान माप के होते हैं।
समांतर चतुर्भुज प्रतीक
समांतर चतुर्भुज प्रतीक समांतर/चतुर्भुज का दाशमिक नाम
▰ काला समांतर चतुर्भुज (Black Parallelogram)
▱ सफेद समांतर चतुर्भुज (White Parallelogram)
प्रश्न:12.क्या एक आयत और समांतर चतुर्भुज का क्षेत्रफल समान है? (Is the area of a rectangle and parallelogram the same?):
उत्तर:चूँकि समांतर चतुर्भुज और आयत समान भागों से बने होते हैं,इसलिए उनका क्षेत्रफल समान होना चाहिए।(वे क्षेत्रफल समान क्यों हैं,इसके बारे में अधिक जानने के लिए क्षेत्रफल की परिभाषा देखें।)
प्रश्न:13.समांतर चतुर्भुज के किसी भी भुजा को क्या कहा जाता है? (What is any side of a parallelogram called?):
उत्तर:एक समांतर चतुर्भुज एक चतुर्भुज है जिसमें विपरीत भुजाएं समानांतर होते हैं (और इसलिए विपरीत कोण बराबर होते हैं)।समान भुजाओं वाला एक चतुर्भुज समचतुर्भुज कहलाता है और एक समांतर चतुर्भुज जिसके सभी कोण समकोण हों,आयत कहलाता है।
प्रश्न:14.समांतर चतुर्भुज और त्रिभुजों के क्षेत्रफलों की प्रमेय कक्षा 9 (Theorems of Areas of Parallelograms and Triangles Class 9):
उत्तर:एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समान्तर रेखा युग्म के साथ स्थित हो तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
प्रश्न:15.समांतर चतुर्भुज प्रमेय कक्षा 9 (Parallelogram Theorem Class 9):
उत्तर:एक ही आधार और एक ही समांतर रेखाओं के बीच के समांतर चतुर्भुजों के क्षेत्रफल बराबर होते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा समांतर चतुर्भुज के क्षेत्रफल का प्रमेय (Theorem of Area of Parallelogram),समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल प्रमेयों के प्रमाण कक्षा 9 (Areas of Parallelograms and Triangles Class 9 Theorems Proofs) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |