Volume of Solids of Revolution
1.परिक्रमण ठोसों के आयतन का परिचय (Introduction to Volume of Solids of Revolution)-
परिक्रमण ठोसों के आयतन (Volume of Solids of Revolution) ज्ञात करने का तात्पर्य है कि जब समतल में स्थित एक स्थिर रेखा के सापेक्ष समतल क्षेत्र परिक्रमा करता है तो एक ठोस का निर्माण करता है।
उदाहरणार्थ एक अर्धवृत्ताकार पटल को इसके व्यास के सापेक्ष (परित:) परिक्रमा करता है तो यह एक ठोस गोले काम निर्माण करता है।
इसी प्रकार जब अर्ध वृत्त चाप इसके सापेक्ष परिक्रमा करता है तो यह एक गोले के पृष्ठ का निर्माण करता है।
इस प्रकार प्राप्त ठोसों के आयतन तथा पृष्ठ परिक्रमण ठोसों के आयतन तथा पृष्ठ कहलाते हैं।स्थिर रेखा को घूर्णन-अक्ष (axis of rotation) कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Evaluation of Triple Integral
2.परिक्रमण ठोसों के आयतन (Volume of Solids of Revolution),आप एक ठोस परिक्रमण का आयतन कैसे पाते हैं? (How do you find the volume of a solid revolution?),परिक्रमण के आयतन का सूत्र (volume of revolution formula)-
(1.)यदि वक्र y=f(x),x-अक्ष के परित: परिक्रमा करता है,तो परिक्रमण ठोस का आयतन (Volume) होता है।
\int _{ a }^{ b }{ \pi { y }^{ 2 }dx }
जहां f(x) अन्तराल (a,b) में एक सीमित,एक-मानीय तथा सतत् फलन है तथा घूर्णन-अक्ष अर्थात् x-अक्ष को अन्तराल (a,b) में नहीं काटता।
(If the area bounded by the curve y=f(x) ,x-axis and the ordinates x=a,x=b revolves about x-axis,the Volume of the solid generated is given by \int _{ a }^{ b }{ \pi { y }^{ 2 }dx } ,it being given that f(x) is finite single valued and continuous in the interval (a,b),y=f(x) does not cross the x-axis in the interval.)
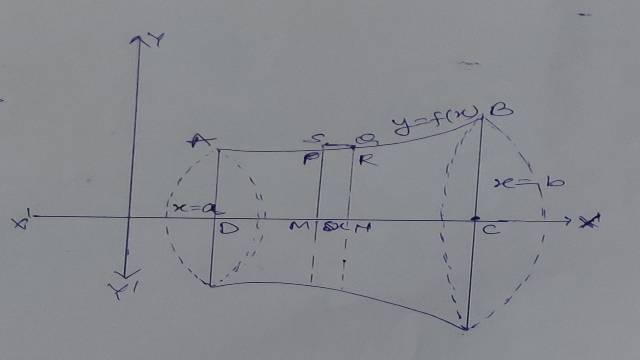
मान लो वक्र AB का समीकरण y=f(x) है और AD और BC क्रमशः x=a तथा x=b कोटियां (Ordinates) है।
वक्र पर कोई बिन्दु P(x,y) लो और मानलो कि इसकी कोटि PM है। पुनः वक्र पर P के अति निकट पर दूसरा बिन्दु Q(x+\delta x,y+\delta y)nलो और मानलो कि इसकी कोटि QN है।
अब मानलो क्षेत्रफलों APMD तथा AQND द्वारा x-अक्ष के सापेक्ष परिक्रमण ठोसों के आयतन क्रमशः V तथा V+\delta Vहै।तब स्पष्टतया क्षेत्रफल PQNM द्वारा x-अक्ष के सापेक्ष परिक्रमण ठोस का आयतन \delta Vहोगा।
अब PM=y ,QN= y+\delta y तथा MN= \delta x
आयत PRNM द्वारा परिक्रमण ठोस का आयतन=\pi { y }^{ 2 }\delta x
तथा आयत SQNM द्वारा परिक्रमण ठोस का आयतन=\pi { (y+\delta y) }^{ 2 }\delta x
यहां यह स्पष्ट है कि क्षेत्रफल PQNM द्वारा परिक्रमण ठोस का आयतन \delta Vअर्थात् आयतों PRNM तथा SQNM द्वारा परिक्रमण ठोसों के आयतनों के मध्य स्थित है
\therefore \pi { y }^{ 2 }\delta x<\delta V<\pi { (y+\delta y) }^{ 2 }\delta x
या \pi { y }^{ 2 }<\frac { \delta V }{ \delta x } <\pi { (y+\delta y) }^{ 2 }....(1)
अब सीमा लेने पर यदि \delta x\rightarrow 0 तो \delta y\rightarrow 0और तब (1) से
\pi { y }^{ 2 }<\begin{matrix} lim \\ \delta x\rightarrow 0 \end{matrix}\frac { \delta V }{ \delta x } <\pi { y }^{ 2 }
या \pi { y }^{ 2 }<\frac { dV }{ dx } <\pi { y }^{ 2 }
अतः \frac { dV }{ dx } =\pi { y }^{ 2 }....(2)
अब x=a तथा x=b सीमाओं के बीच (2) का x के सापेक्ष समाकलन करने पर-
\int _{ a }^{ b }{ \pi { y }^{ 2 }dx } =\int _{ a }^{ b }{ \frac { dV }{ dx } dx } =\int _{ a }^{ b }{ dV } ={ [V] }_{ a }^{ b }
=[V का मान जब x=b]-[V का मान जब x=a]
=क्षेत्रफल ABCD के परिक्रमण द्वारा जनित ठोस का आयतन
=वक्र के चाप AB ,x-अक्ष एवं कोटियों x=a तथा x=b से घिरे क्षेत्रफल द्वारा x के सापेक्ष परिक्रमण ठोस का आयतन
(2.)वक्र x=f(y) ,y-अक्ष एवं भुजों y=c ,y=d के मध्य घिरे क्षेत्रफल द्वारा y-अक्ष के सापेक्ष परिक्रमण-ठोस का आयतन होगा।
\int _{ c }^{ d }{ \pi { x }^{ 2 }dy }
(3.)यदि वक्र का समीकरण ध्रुवीय रूप में अर्थात् r=f\left( \theta \right) और यदि वक्र प्रारम्भिक रेखा (Initial line) के सापेक्ष परिक्रमा करे,तब इस प्रकार जनित ठोस का आयतन होगा।
\int _{ a }^{ b }{ \pi { y }^{ 2 }dx } =\int _{ \alpha }^{ \beta }{ \pi { y }^{ 2 }(\frac { dx }{ d\theta } ) } d\theta
जहां \theta =\alpha जब x=a और\theta =\beta जब x=b
परन्तु x=r\cos { \theta } ,y=r\sin { \theta }
आयतन=\int _{ \alpha }^{ \beta }{ \pi { (r\cos { \theta } ) }^{ 2 }\frac { d(r\cos { \theta } ) }{ d\theta } } d\theta
(4.) यदि वक्र का समीकरण प्राचलिक रूप में हो, अर्थात्
x=f\left( t \right) ,y=\phi (t)
हो,तो वक्र x-अक्ष एवं कोटियों x=a तथा x=b के बीच घिरे क्षेत्रफल द्वारा x-अक्ष के सापेक्ष परिक्रमण-ठोस का आयतन होगा।
\int _{ a }^{ b }{ \pi { y }^{ 2 }dx } =\int _{ m }^{ n }{ \pi { y }^{ 2 }\frac { dx }{ dt } . } dt
या \int _{ a }^{ b }{ \pi { y }^{ 2 }dx } =\int _{ m }^{ n }{ \pi { [\phi (t)] }^{ 2 }f^{ \prime }\left( t \right) } dt
जहां t=m,जब x=a और t=n जब x=b
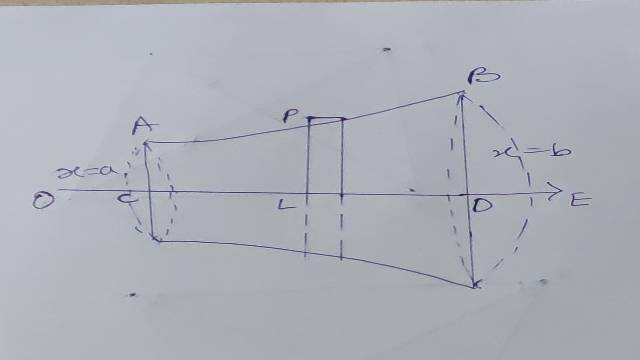
(5.)यदि वक्र AB,निर्देश-अक्षों के अलावा किसी अन्य रेखा OE (मानलो) के सापेक्ष परिक्रमा करता है,तो परिक्रमण ठोस का आयतन होगा।
\int _{ OC }^{ OD }{ \pi { (PL) }^{ 2 }d(OL) }
जहां O, घूर्णन-अक्ष OE पर एक स्थिर बिन्दु (fixed point) है तथा PL वक्र पर किसी बिन्दु P से घूर्णन-अक्ष पर लम्ब (Perpendicular) है।
(6.)यदि वक्र y=f(x),x-अक्ष के बजाय इसके समान्तर किसी रेखा y=c (मानलो) के सापेक्ष परिक्रमण करता है,तो परिक्रमण ठोस का आयतन होगा।
\int _{ a }^{ b }{ { (y-c) }^{ 2 }dx }
क्योंकि यहां वक्र के किसी बिन्दु की घूर्णन अक्ष से लाम्बिक दूरी (perpendicular distance) y-c होगी।
इसी प्रकार यदि वक्र x=f(y),y-अक्ष के बजाए इसके समान्तर किसी रेखा x=a (मानलो) के सापेक्ष परिक्रमा करता है, तो परिक्रमण ठोस का आयतन होगा।
\int _{ c }^{ d }{ { \pi (x-a) }^{ 2 }dy }
3.परिक्रमण ठोसों के आयतन के उदाहरण (Volume of Solids of Revolution Examples),परिक्रमण ठोस अभ्यास समस्याओं और समाधान (volumes of solids of revolution practice problems and solutions)-
Example-1.दीर्घवृत्त \frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1 नाभिलम्ब द्वारा कटा हुआ भाग निकटतर शीर्ष पर स्पर्श रेखा के सापेक्ष परिक्रमा करता है।इस प्रकार जनित रील का आयतन ज्ञात कीजिए।
(The part of the ellipse \frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1 cut off by a latus rectum revolves about the tangent at the nearer vertex.Find the volume of the reel thus generated.)
Solution-
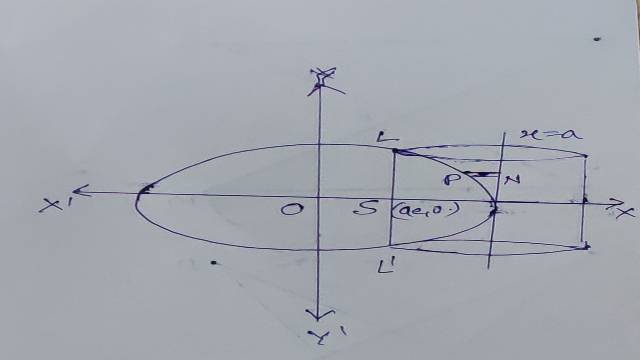
माना कि नाभिलम्ब LSL’ है।वक्र के बिन्दु P(x,y) से x=a पर लम्ब की लम्बाई=a-x
PN=OA-OK=a-x
पट्टिका द्वारा जनित आयतन=\pi { (a-x) }^{ 2 }\delta y
नाभिलम्ब की लम्बाई=\frac { 2{ b }^{ 2 } }{ a }
अतःLS=\frac { { b }^{ 2 } }{ a }
अभीष्ट आयतन==2\int _{ 0 }^{ \frac { { b }^{ 2 } }{ a } }{ \pi { (a-x) }^{ 2 }dy }
=2\pi \int _{ 0 }^{ \frac { { b }^{ 2 } }{ a } }{ [{ a }^{ 2 }-2ax+{ x }^{ 2 }]dy } \\ =2\pi \int _{ 0 }^{ \frac { { b }^{ 2 } }{ a } }{ [{ a }^{ 2 }-2a.\frac { a }{ b } \sqrt { { b }^{ 2 }-{ y }^{ 2 } } +\frac { { a }^{ 2 } }{ { b }^{ 2 } } ({ b }^{ 2 }-{ y }^{ 2 })]dy } \\ =\frac { { 2\pi a }^{ 2 } }{ { b }^{ 2 } } \int _{ 0 }^{ \frac { { b }^{ 2 } }{ a } }{ [2{ b }^{ 2 }-2b\sqrt { { b }^{ 2 }-{ y }^{ 2 } } -{ y }^{ 2 }]dy } \\ =\frac { { 2\pi a }^{ 2 } }{ { b }^{ 2 } } { [2{ b }^{ 2 }y-2b\{ \frac { 1 }{ 2 } y\sqrt { { b }^{ 2 }-{ y }^{ 2 } } +{ \frac { 1 }{ 2 } b }^{ 2 }\sin ^{ -1 }{ (\frac { y }{ b } ) } -\frac { 1 }{ 3 } { y }^{ 3 }\} ] }_{ 0 }^{ \frac { { b }^{ 2 } }{ a } }\\ =\frac { { 2\pi a }^{ 2 } }{ { b }^{ 2 } } { [\frac { 2{ b }^{ 4 } }{ a } -\frac { { b }^{ 4 } }{ { a }^{ 2 } } \sqrt { { a }^{ 2 }-{ b }^{ 2 } } -{ b }^{ 3 }\sin ^{ -1 }{ (\frac { b }{ a } ) } -\frac { 1 }{ 3 } \frac { { b }^{ 6 } }{ { a }^{ 3 } } ] }\\ =\frac { 2\pi b }{ 3a } { [2b{ a }^{ 2 }-ba\sqrt { { a }^{ 2 }{ e }^{ 2 } } -{ a }^{ 3 }\sin ^{ -1 }{ \sqrt { 1-{ e }^{ 2 } } } -\frac { 1 }{ 3 } { b }^{ 3 }] }\\ =\frac { 2\pi b }{ 3a } { [6{ a }^{ 2 }b-{ b }^{ 3 }-3ab\sqrt { { a }^{ 2 }-{ b }^{ 2 } } -3{ a }^{ 3 }\sin ^{ -1 }{ (\frac { b }{ a } ) } ] }
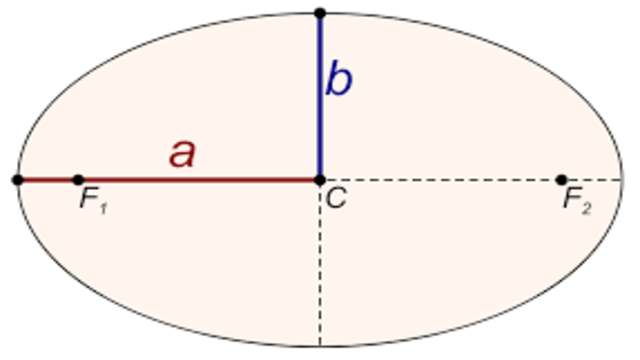
Example-2.सिद्ध कीजिए की दीर्घवृत्त \frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1 को लघुअक्ष के सापेक्ष घुमाने से जनित ठोस का आयतन, दीर्घवृत्त एवं सहायक वृत्त को दीर्घ अक्ष के सापेक्ष घुमाने से जनित आयतनों का मध्यानुपाती होता है।
(Prove that volume of solid generated by the revolution of the ellipse\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1 about it’s minor axis is the mean proportional between those generated by the revolution of the ellipse and of the auxiliary circle about the major axis.)
Solution-दीर्घवृत्त को लघु अक्ष अर्थात् y-अक्ष के परित घुमाने पर क्षेत्रफल y=0 तथा y=b भुज द्वारा घिरा हुआ है।
अतः अभीष्ट आयतन=2\int _{ 0 }^{ b }{ \pi { x }^{ 2 }dy } \\ { V }_{ 1 }=2\pi \int _{ 0 }^{ b }{ \frac { { a }^{ 2 } }{ { b }^{ 2 } } ({ b }^{ 2 }-{ y }^{ 2 })dy } \\ =\frac { { 2\pi a }^{ 2 } }{ { b }^{ 2 } } { [{ b }^{ 2 }y-\frac { { y }^{ 3 } }{ 3 } ] }_{ 0 }^{ b }\\ =\frac { { 2\pi a }^{ 2 } }{ { b }^{ 2 } } { [{ b }^{ 3 }-\frac { { b }^{ 3 } }{ 3 } ] }\\ =\frac { { 2\pi a }^{ 2 } }{ { b }^{ 2 } } { [\frac { 2{ b }^{ 3 } }{ 3 } ] }\\ =\frac { { 4\pi a }^{ 2 }b }{ 3 }
दीर्घवृत्त को दीर्घ अक्ष के परित घुमाने पर क्षेत्रफल x=0 तथा x=a कोटियों द्वारा घिरा हुआ है।
अतः अभीष्ट आयतन { V }_{ 2 }=2\int _{ 0 }^{ a }{ \pi { y }^{ 2 }dx } \\ =2\pi \int _{ 0 }^{ a }{ \frac { { b }^{ 2 } }{ { a }^{ 2 } } ({ a }^{ 2 }-{ x }^{ 2 })dx } \\ =\frac { 2\pi { b }^{ 2 } }{ { a }^{ 2 } } { [{ a }^{ 2 }x-\frac { { x }^{ 3 } }{ 3 } ] }_{ 0 }^{ a }\\ =\frac { { 2\pi b }^{ 2 } }{ { a }^{ 2 } } { [{ a }^{ 3 }-\frac { { a }^{ 3 } }{ 3 } ] }\\ =\frac { { 2\pi b }^{ 2 } }{ { a }^{ 2 } } { [\frac { 2{ a }^{ 3 } }{ 3 } ] }\\ =\frac { { 4\pi ab }^{ 2 } }{ 3 }
सहायक वृत्त को दीर्घ अक्ष के सापेक्ष घुमाने पर क्षेत्रफल x=0 तथा x=a कोटियों द्वारा घिरा हुआ है।
अतः अभीष्ट आयतन { V }_{ 3 }=2\int _{ 0 }^{ a }{ \pi { y }^{ 2 }dx } \\ =2\int _{ 0 }^{ a }{ \pi ({ a }^{ 2 }-{ x }^{ 2 })dx } \\ =2\pi { [{ a }^{ 2 }x-\frac { { x }^{ 3 } }{ 3 } ] }_{ 0 }^{ a }\\ =2\pi { [{ a }^{ 3 }-\frac { { a }^{ 3 } }{ 3 } ] }\\ =2\pi { [\frac { 2{ a }^{ 3 } }{ 3 } ] }\\ =\frac { 4\pi { a }^{ 3 } }{ 3 }
मध्यानुपाती V= \sqrt { { V }_{ 3 }{ V }_{ 2 } } \\ =\sqrt { \frac { { 4\pi ab }^{ 2 } }{ 3 } \times \frac { 4\pi { a }^{ 3 } }{ 3 } } \\ =\sqrt { \frac { 16{ \pi }^{ 2 }{ a }^{ 4 }{ b }^{ 2 } }{ 9 } } \\ =\frac { { 4\pi a }^{ 2 }b }{ 3 }
अतः{ V }_{ 1 }=V
Example-3.उस दीर्घवृत्त द्वारा जनित दीर्घाक्ष एवं लघु-अक्ष गोलाभों के आयतन ज्ञात कीजिए जिनकी दीर्घ अक्ष एवं लघु अक्षें क्रमशः{ (24\pi ) }^{ \frac { 1 }{ 3 } } एवं { (3\pi ) }^{ \frac { 1 }{ 3 } } है।
(Find the volumes of the oblate and prolate spheroids generated by an ellipse whose major and minor axes are { (24\pi ) }^{ \frac { 1 }{ 3 } } and { (3\pi ) }^{ \frac { 1 }{ 3 } }.)
Solution-
दीर्घवृत्त \frac { { x }^{ 2 } }{ { \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } } } +\frac { { y }^{ 2 } }{ \frac { { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } } =1 को दीर्घाक्ष के परित घुमाने पर जनित आयतन { V }_{ 1 }=2\int _{ 0 }^{ \frac { { (24\pi ) }^{ \frac { 1 }{ 3 } } }{ 2 } }{ \pi { y }^{ 2 }dx } \\ { V }_{ 1 }=2\pi \int _{ 0 }^{ \frac { { (24\pi ) }^{ \frac { 1 }{ 3 } } }{ 2 } }{ \frac { { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } \times \frac { 4 }{ { (24\pi ) }^{ \frac { 2 }{ 3 } } } { \left[ \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } -{ x }^{ 2 } \right] }dx } \\ { V }_{ 1 }=2\pi \frac { { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } \times \frac { 4 }{ { (24\pi ) }^{ \frac { 2 }{ 3 } } } { \left[ \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } x-\frac { { x }^{ 3 } }{ 3 } \right] }_{ 0 }^{ \frac { { (24\pi ) }^{ \frac { 1 }{ 3 } } }{ 2 } }\\ \\ =\frac { 2\pi { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ { (24\pi ) }^{ \frac { 2 }{ 3 } } } \left[ \frac { 24\pi }{ 8 } -\frac { 24\pi }{ 24 } \right] \\ =\frac { 2\pi { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ { (24\pi ) }^{ \frac { 2 }{ 3 } } } 2\pi \\ =4{ \pi }^{ 2 }\frac { { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ { (24\pi ) }^{ \frac { 2 }{ 3 } } } \\ =4{ \pi }^{ 2 }{ (\frac { 1 }{ 8 } ) }^{ \frac { 2 }{ 3 } }=4{ \pi }^{ 2 }\times \frac { 1 }{ 4 } ={ \pi }^{ 2 }
दीर्घ वृत्त को लघु अक्ष के परित घुमाने पर जनित
अभीष्ट आयतन { V }_{ 2 }=2\int _{ 0 }^{ \frac { { (3\pi ) }^{ \frac { 1 }{ 3 } } }{ 2 } }{ \pi { x }^{ 2 }dx } \\ { V }_{ 2 }=2\pi \int _{ 0 }^{ \frac { { (3\pi ) }^{ \frac { 1 }{ 3 } } }{ 2 } }{ \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ { (3\pi ) }^{ \frac { 2 }{ 3 } } } \left[ \frac { { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } -{ y }^{ 2 } \right] dy } \\ =2\pi \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ { (3\pi ) }^{ \frac { 2 }{ 3 } } } { \left[ \frac { { (3\pi ) }^{ \frac { 2 }{ 3 } } }{ 4 } y-\frac { { y }^{ 3 } }{ 3 } \right] }_{ 0 }^{ \frac { { (3\pi ) }^{ \frac { 1 }{ 3 } } }{ 2 } }\\ =2\pi \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ { (3\pi ) }^{ \frac { 2 }{ 3 } } } \left( \frac { 3\pi }{ 8 } -\frac { 3\pi }{ 24 } \right) \\ =2\pi \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ { (3\pi ) }^{ \frac { 2 }{ 3 } } } .\frac { \pi }{ 4 } \\ =\frac { { \pi }^{ 2 } }{ 2 } \frac { { (24\pi ) }^{ \frac { 2 }{ 3 } } }{ { (3\pi ) }^{ \frac { 2 }{ 3 } } } \\ =\frac { { \pi }^{ 2 } }{ 2 } .4\\ =2{ \pi }^{ 2 }
इन उदाहरणों के द्वारा परिक्रमण ठोसों के आयतन (Volume of Solids of Revolution) को समझा जा सकता है।
4.परिक्रमण ठोसों के आयतन की समस्याएं (Volume of Solids of Revolution Problems)-
(1.)कैटिनरी y=c\cosh { (\frac { x }{ c } ) } के एक चाप को x-अक्ष के चारों ओर घुमाने से बने ठोस का आयतन ज्ञात कीजिए।
(Find the volume generated by the revolution of the catenary y=c\cosh { (\frac { x }{ c } ) } about x-axis.)
(2.)वक्रx={ t }^{ 2 },y=t-\frac { 1 }{ 3 } { t }^{ 3 } के लूप को x-अक्ष के सापेक्ष घुमाने से जनित ठोस का आयतन ज्ञात कीजिए।
(Find the volume generated by the revolution of the loop of the curvex={ t }^{ 2 },y=t-\frac { 1 }{ 3 } { t }^{ 3 } about x-axis.)
(3.) प्रदर्शित कीजिए कि साइक्लाॅइड x=a(\theta +\sin { \theta } ),y=a(1-\cos { \theta } ),0\le \theta \le \pi को y-अक्ष के सापेक्ष घुमाने से जनित ठोस का आयतन \pi { a }^{ 3 }(\frac { 3 }{ 2 } { \pi }^{ 2 }-\frac { 8 }{ 3 } ) है।
(4.)साइक्लाॅइडx=a(\theta +\sin { \theta } ),y=a(1-\cos { \theta } ) को शीर्ष पर स्पर्श रेखा के सापेक्ष घुमाने से बनी रील का आयतन है।
(Show that the volume of the reel formed by the revolution of the cycloid x=a(\theta +\sin { \theta } ),y=a(1-\cos { \theta } ) about the tangent at the vertex is{ \pi }^{ 2 }{ a }^{ 3 }.)
(5.) निम्नलिखित वक्र की लूप को x-अक्ष के सापेक्ष घुमाने से बने ठोसों का आयतन ज्ञात कीजिए।
(Find the volume of solid formed by revolution of the loop of the following curves,about x-axis.)
{ y }^{ 2 }(a-x)={ x }^{ 2 }(a+x)
उपर्युक्त सवालों को हल करने पर परिक्रमण ठोसों के आयतन (Volume of Solids of Revolution) ठीक से समझ में आ जाएगा।
5.परिक्रमण का आयतन (Volume of revolution), ठोस का आयतन क्या है? (What is the volume of the solid?)-
परिक्रमण का एक ठोस समतल में एक रेखा के बारे में समतल में एक फ़ंक्शन को घुमाकर प्राप्त एक तीन-आयामी वस्तु है।इस ठोस की आयतन की गणना समाकलन के माध्यम से की जा सकती है।आयतन ज्ञात करने के सामान्य तरीके हैं डिस्क विधि, शेल विधि और पेप्पस का केन्द्रक प्रमेय।
6.परिक्रमण के ठोस पदार्थ कौन से हैं? (Which are the solids of revolution?)-
एक प्रतिनिधि डिस्क परिक्रमण के एक ठोस के तीन आयामी आयतन तत्व है।परिक्रमण के एक ठोस का आयतन को खोजने के लिए दो सामान्य तरीके डिस्क विधि और समाकलन की शैल विधि हैं।
Also Read This Article:-Double Integral in Polar Coordinates
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |