Evaluation of Triple Integral
1.त्रि समाकलन का मान ज्ञात करना का परिचय (Introduction to Evaluation of Triple Integral)-
त्रि समाकलन का मान ज्ञात करना (Evaluation of Triple Integral ) सीखेंगे।त्रि समाकलन का सीधा-सादा अर्थ है किसी फलन का तीन बार समाकलन करना।सामान्यतया किसी क्षेत्र का तीन बार समाकलन करने की आवश्यकता तब पड़ती है जब हम उसका आयतन ज्ञात करना चाहते हों।
माना कि त्रिविम समष्टि में (Three dimensional space) में V कोई क्षेत्र है।मान लो फलन f(xy,z) क्षेत्र V के प्रत्येक बिन्दु पर परिभाषित है।
क्षेत्र V को प्रारम्भिक आयतनों (Elementary Volumed) \delta { V }_{ 1 },\delta { V }_{ 2 },.....,\delta { V }_{ n } में विभाजित कीजिए।प्रत्येक उपभाग में स्वेच्छ बिन्दु (arbitrary point) लो।निम्न योगफल पर विचार करते हैं-
\overset { n }{ \underset { k=1 }{ \sum { \quad } } } f\left( { x }_{ k },{ y }_{ k },{ z }_{ k } \right) \delta { V }_{ k }...(1)
विभाजित क्षेत्रों की संख्या n इस प्रकार अनन्त होने दो कि की अधिकतम सीमा शून्य की ओर अग्रसर हो।यदि इन प्रतिबन्धों के सीमा का अस्तित्व
\underset { n\rightarrow \infty }{ lim } \overset { n }{ \underset { k=1 }{ \sum { \quad } } } f\left( { x }_{ k },{ y }_{ k },{ z }_{ k } \right) \delta { V }_{ k }...(2)
(Existence) हो जो विभाजित क्षेत्रों के उप-विभाजन की विधि (mode of subdivision) से स्वतन्त्र हो तो उस सीमा को क्षेत्र V पर f(x,y,z) का त्रिसमाकलन (Triple Integration) कहते हैं और इसे निम्न प्रकार से प्रकट करते हैं:
\int { \int { \int _{ V }^{ \quad }{ f\left( x,y,z \right) } dV } }
अतः \int { \int { \int _{ V }^{ \quad }{ f\left( x,y,z \right) } dV } } =\underset { n\rightarrow \infty }{ lim } \overset { n }{ \underset { k=1 }{ \sum { \quad } } } f\left( { x }_{ k },{ y }_{ k },{ z }_{ k } \right) \delta { V }_{ k }
यह दिखाया जा सकता है कि सीमा का अस्तित्व होगा यदि क्षेत्र V की सीमा (boundary) पर या भीतर सभी बिन्दुओं पर f(x,y,z) संतत (continuous) हो या खण्डश: संतत (piecewise continuous) हो।
Also Read This Article:-convert integral to polar coordinates
2.त्रि समाकलन का मान ज्ञात करना (Evaluation of Triple Integral )-
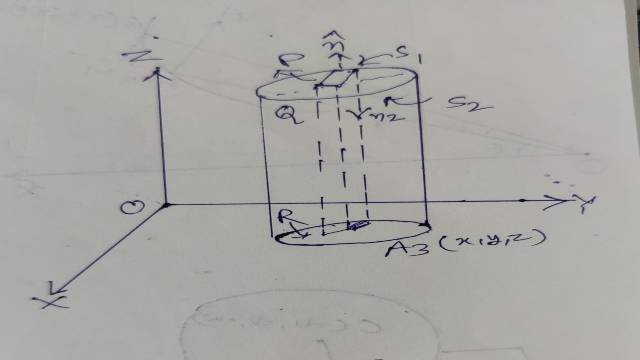
माना त्रिविम समष्टि में V कोई क्षेत्र है।क्षेत्र V को तीन निर्देशांक तलों (Coordinate planes)के समान्तर तल खींचकर छोटे-छोटे घनों (coboids) में विभाजित करो।
आयतन V को सभी उर्ध्वाधर स्तम्भों (Vertical Columns) के आयतनों का योग माना जा सकता है जिनकी निम्न सीमा (lower boundary) पृष्ठ (Surface) z={ z }_{ 1 }\left( x,y \right) (मान लो) तथा उच्च सीमा (upper boundary), पृष्ठ (surface)z={ z }_{ 2 }\left( x,y \right) से घिरी हुई है।इन स्तम्भों के आधार क्षेत्र\delta { A }_{ r } है जो कि xy समतल के किसी क्षेत्र को घेरे हुए है।
अतः सर्वप्रथम क्षेत्र \delta { A }_{ r } पर खड़े स्तम्भ घन का योग करते हैं,फिर xy-तल के क्षेत्र A पर प्रत्येक स्तम्भ के आयतन का योग करते हैं। अतः
\sum { \quad } f\left( { x }_{ k },{ y }_{ k },{ z }_{ k } \right) \delta { V }_{ k }=\underset { r }{ \sum { \quad } } \left\{ \underset { \quad }{ \sum { \quad } f\left( { x }_{ r },{ y }_{ r },{ z }_{ r } \right) \delta z } \right\} \delta { A }_{ r }..(1)
जहां बिन्दु \left( { x }_{ k },{ y }_{ k },{ z }_{ k } \right) क्षेत्र \delta { A }_{ r } पर खड़े k वें घन में स्थित है।
अब सीमा लेने पर,जब \delta { A }_{ r }\rightarrow 0 तथा \delta z\rightarrow 0 तो (1) को निम्न प्रकार से लिखा जा सकता है।
\underset { \delta { A }_{ r }\rightarrow 0 }{ lim } \sum { \quad } f\left( { x }_{ k },{ y }_{ k },{ z }_{ k } \right) \delta { V }_{ k }=\int { \int _{ A }^{ \quad }{ \left\{ \int _{ { z }_{ 1 }\left( x,y \right) }^{ { z }_{ 2 }\left( x,y \right) }{ f\left( x,y,z \right) } \right\} } } dA
या \int { \int { \int _{ V }^{ \quad }{ f\left( x,y,z \right) } dV } } =\int { \int _{ A }^{ \quad }{ \left\{ \int _{ { z }_{ 1 }\left( x,y \right) }^{ { z }_{ 2 }\left( x,y \right) }{ f\left( x,y,z \right) } \right\} } } dA...(2)
अब यदि क्षेत्र A वक्रों y={ y }_{ 1 }\left( x \right) ,y={ y }_{ 2 }\left( x \right) , x=a तथा x=b से घिरा हुआ हो तो (2) को निम्न प्रकार लिखा जा सकता है:
\int { \int { \int _{ V }^{ \quad }{ f\left( x,y,z \right) } dV } } =\int _{ b }^{ a }{ \int _{ { y }_{ 1 }\left( x \right) }^{ { y }_{ 2 }\left( x \right) }{ \left\{ \int _{ { z }_{ 1 }\left( x,y \right) }^{ { z }_{ 2 }\left( x,y \right) }{ f\left( x,y,z \right) } dz \right\} dydx } }
या \int { \int { \int _{ V }^{ \quad }{ f\left( x,y,z \right) } dV } } =\int _{ b }^{ a }{ \int _{ { y }_{ 1 }\left( x \right) }^{ { y }_{ 2 }\left( x \right) }{ \int _{ { z }_{ 1 }\left( x,y \right) }^{ { z }_{ 2 }\left( x,y \right) }{ f\left( x,y,z \right) } dxdydz } }
जहां सर्वप्रथम x तथा y को अचर मानते हुए z के सापेक्ष समाकलन किया जाता है,इसके बाद x को अचर मानते हुए y के सापेक्ष समाकलन किया जाता है और अन्त में x के सापेक्ष समाकलन किया जाता है।
3.त्रि समाकलन का मान ज्ञात करना (Evaluation of Triple Integral ) पर आधारित सवाल,ट्रिपल इंटीग्रल की हल की गई समस्याएं (Triple integrals solved problems),ट्रिपल इंटीग्रल उदाहरण (Triple integral examples )-
निम्नलिखित त्रि-समाकलों का मान ज्ञात कीजिए-
(Evaluate the following triple integrals)
Question-1.\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ z }^{ 2 } } }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ y }^{ 2 }-{ z }^{ 2 } } }{ \left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } \right) dxdydz } } }
Solution-\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ z }^{ 2 } } }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ y }^{ 2 }-{ z }^{ 2 } } }{ \left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } \right) dxdydz } } } \\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ z }^{ 2 } } }{ { \left[ \frac { { x }^{ 3 } }{ 3 } +x{ y }^{ 2 }+x{ z }^{ 2 } \right] }_{ 0 }^{ \sqrt { { a }^{ 2 }-{ y }^{ 2 }-{ z }^{ 2 } } } } } dydz\\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ z }^{ 2 } } }{ { \quad } } } [\frac { 1 }{ 3 } { \left( { a }^{ 2 }-{ y }^{ 2 }-{ z }^{ 2 } \right) }^{ \frac { 3 }{ 2 } }+\sqrt { { a }^{ 2 }-{ y }^{ 2 }-{ z }^{ 2 } } { y }^{ 2 }+\sqrt { { a }^{ 2 }-{ y }^{ 2 }-{ z }^{ 2 } } { z }^{ 2 }]dydz\\ put\quad y=\sqrt { { a }^{ 2 }-{ z }^{ 2 } } \sin { \theta } \Rightarrow dy=\sqrt { { a }^{ 2 }-{ z }^{ 2 } } \cos { \theta } d\theta
जब y=0 तो \theta =0 जब y=\sqrt { { a }^{ 2 }-{ z }^{ 2 } } तो \theta =\frac { \pi }{ 2 }
=\int _{ 0 }^{ a }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { \quad } } } [\frac { 1 }{ 3 } { [{ a }^{ 2 }-{ z }^{ 2 }-({ a }^{ 2 }-{ z }^{ 2 })\sin ^{ 2 }{ \theta } ] }^{ \frac { 3 }{ 2 } }+\sqrt { { a }^{ 2 }-{ z }^{ 2 }-({ a }^{ 2 }-{ z }^{ 2 })\sin ^{ 2 }{ \theta } } ({ a }^{ 2 }-{ z }^{ 2 })\sin ^{ 2 }{ \theta } +(\sqrt { { a }^{ 2 }-{ z }^{ 2 }-({ a }^{ 2 }-{ z }^{ 2 })\sin ^{ 2 }{ \theta } } ){ z }^{ 2 }]({ a }^{ 2 }-{ z }^{ 2 })\cos { \theta } d\theta dz\\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { \quad } } } [\frac { 1 }{ 3 } { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ \frac { 3 }{ 2 } }{ (1-\sin ^{ 2 }{ \theta } ) }^{ \frac { 3 }{ 2 } }+{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ \frac { 3 }{ 2 } }\sqrt { 1-\sin ^{ 2 }{ \theta } } \sin ^{ 2 }{ \theta } +{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ \frac { 1 }{ 2 } }(\sqrt { 1-\sin ^{ 2 }{ \theta } } ){ z }^{ 2 }]({ a }^{ 2 }-{ z }^{ 2 })\cos { \theta } d\theta dz\\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \quad } } { \quad }[\frac { 1 }{ 3 } { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ \frac { 3 }{ 2 } }\cos ^{ 3 }{ \theta } +{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ \frac { 3 }{ 2 } }\cos { \theta } \sin ^{ 2 }{ \theta } +{ z }^{ 2 }{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ \frac { 1 }{ 2 } }\cos { \theta } ]\sqrt { ({ a }^{ 2 }-{ z }^{ 2 }) } \cos { \theta } d\theta dz\\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { \quad } } } [\frac { 1 }{ 3 } { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }\cos ^{ 4 }{ \theta } +{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }\cos ^{ 2 }{ \theta } \sin ^{ 2 }{ \theta } +{ ({ a }^{ 2 }-{ z }^{ 2 }) }{ z }^{ 2 }\cos ^{ 2 }{ \theta } ]d\theta \\ =\int _{ 0 }^{ a }{ \quad } [\frac { 1 }{ 3 } \frac { \Gamma (\frac { 4+1 }{ 2 } )\Gamma (\frac { 0+1 }{ 2 } ) }{ 2\Gamma (\frac { 4+0+2 }{ 2 } ) } { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }+{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }\frac { \Gamma (\frac { 2+1 }{ 2 } )\Gamma (\frac { 2+1 }{ 2 } ) }{ 2\Gamma (\frac { 2+2+2 }{ 2 } ) } +{ { z }^{ 2 }({ a }^{ 2 }-{ z }^{ 2 })\frac { \Gamma (\frac { 2+1 }{ 2 } )\Gamma (\frac { 0+1 }{ 2 } ) }{ 2\Gamma (\frac { 2+0+2 }{ 2 } ) } }]d\theta \\ =\int _{ 0 }^{ a }{ \quad } [\frac { 1 }{ 3 } \frac { \frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } \sqrt { \pi } }{ 2\times 2 } { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }+{ ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }\frac { \frac { 1 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } \sqrt { \pi } }{ 2\times 2 } +{ ({ a }^{ 2 }-{ z }^{ 2 }){ z }^{ 2 }\frac { \frac { 1 }{ 2 } \sqrt { \pi } \sqrt { \pi } }{ 2\times 1 } }]d\theta \\ =\int _{ 0 }^{ a }{ [\frac { 1 }{ 16 } \pi { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }+\frac { 1 }{ 16 } { ({ a }^{ 2 }-{ z }^{ 2 }) }^{ 2 }\pi +\frac { 1 }{ 4 } \pi { ({ a }^{ 2 }-{ z }^{ 2 }){ z }^{ 2 } }] } d\theta \\ put\quad z=a\sin { \theta } \Rightarrow dz=a\cos { \theta } d\theta
जब z=0 तब \theta =0 जब z=a तब \theta =\frac { \pi }{ 2 }
=\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \quad \quad } [\frac { 1 }{ 16 } \pi { ({ a }^{ 2 }-{ a }^{ 2 }\sin ^{ 2 }{ \theta } ) }^{ 2 }+\frac { 1 }{ 16 } { ({ a }^{ 2 }-{ a }^{ 2 }\sin ^{ 2 }{ \theta } ) }^{ 2 }\pi +\frac { 1 }{ 4 } \pi { ({ a }^{ 2 }-{ a }^{ 2 }\sin ^{ 2 }{ \theta } ){ a }^{ 2 }\sin ^{ 2 }{ \theta } }]a\cos { \theta } d\theta \\ =\pi a\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \quad } [\frac { 1 }{ 16 } { a }^{ 4 }\cos ^{ 4 }{ \theta } +\frac { 1 }{ 16 } { a }^{ 4 }\cos ^{ 4 }{ \theta } +\frac { 1 }{ 4 } { a }^{ 4 }\cos ^{ 4 }{ \theta } { \sin ^{ 2 }{ \theta } }]\cos { \theta } d\theta \\ =\frac { \pi }{ 4 } { a }^{ 5 }\int _{ 0 }^{ \frac { \pi }{ 2 } }{ [\frac { 1 }{ 4 } \cos ^{ 5 }{ \theta } +\frac { 1 }{ 4 } \cos ^{ 5 }{ \theta } +\cos ^{ 3 }{ \theta } { \sin ^{ 2 }{ \theta } }] } d\theta \\ =\frac { \pi }{ 4 } { a }^{ 5 }[\frac { 1 }{ 4 } \frac { \Gamma (\frac { 5+1 }{ 2 } )\Gamma (\frac { 0+1 }{ 2 } ) }{ 2\Gamma (\frac { 5+0+2 }{ 2 } ) } +\frac { \Gamma (\frac { 5+1 }{ 2 } )\Gamma (\frac { 0+1 }{ 2 } ) }{ 2\Gamma (\frac { 5+0+2 }{ 2 } ) } +{ \frac { \Gamma (\frac { 3+1 }{ 2 } )\Gamma (\frac { 2+1 }{ 2 } ) }{ 2\Gamma (\frac { 3+2+2 }{ 2 } ) } }]\\ =\frac { \pi }{ 4 } { a }^{ 5 }[\frac { 1 }{ 4 } (\frac { 2\sqrt { \pi } }{ 2.\frac { 5 }{ 2 } .\frac { 3 }{ 2 } .\frac { 3 }{ 2 } \sqrt { \pi } } )+\frac { 1 }{ 4 } .\frac { 2\sqrt { \pi } }{ 2.\frac { 5 }{ 2 } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } } +\frac { \frac { 1 }{ 2 } \sqrt { \pi } }{ 2.\frac { 5 }{ 2 } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } } ]\\ =\frac { \pi }{ 4 } { a }^{ 5 }[\frac { 2 }{ 15 } +\frac { 2 }{ 15 } +\frac { 2 }{ 15 } ]\\ =\frac { \pi }{ 4 } { a }^{ 5 }[\frac { 6 }{ 15 } ]\\ =\frac { \pi }{ 10 } { a }^{ 5 }
Question-2.\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ 3 }{ \int _{ 0 }^{ 4 }{ ({ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 })dxdydz } } }
Solution–\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ 3 }{ \int _{ 0 }^{ 4 }{ ({ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 })dxdydz } } } \\ =\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ 3 }{ { [\frac { { x }^{ 3 } }{ 3 } +x{ y }^{ 2 }+x{ z }^{ 2 }] }_{ 0 }^{ 4 } } } dydz\\ =\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ 3 }{ { [\frac { 64 }{ 3 } +4{ y }^{ 2 }+4{ z }^{ 2 }] } } } dydz\\ =\int _{ 0 }^{ 2 }{ { [\frac { 64 }{ 3 } y+\frac { 4 }{ 3 } { y }^{ 3 }+4{ yz }^{ 2 }] }_{ 0 }^{ 3 } } dz\\ =\int _{ 0 }^{ 2 }{ { [64+36+12{ z }^{ 2 }] } } dz\\ =\int _{ 0 }^{ 2 }{ { [100z+12{ z }^{ 2 }] } } dz\\ ={ [100+\frac { 12{ z }^{ 3 } }{ 3 } ] }_{ 0 }^{ 2 }\\ =200+4{ (2) }^{ 3 }\\ =200+32\\ =232
Question-3.\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ \int _{ 0 }^{ \frac { { x }^{ 2 }+{ y }^{ 2 } }{ 4 } }{ dxdydz } } }
Solution–\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ \int _{ 0 }^{ \frac { { x }^{ 2 }+{ y }^{ 2 } }{ 4 } }{ dxdydz } } } \\ =\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ { [Z] }_{ 0 }^{ \frac { { x }^{ 2 }+{ y }^{ 2 } }{ 4 } } } } dydx\\ =\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ [\frac { { x }^{ 2 }+{ y }^{ 2 } }{ 4 } ] } } dydx\\ =\frac { 1 }{ 4 } \int _{ 0 }^{ 2 }{ { [{ x }^{ 2 }y+\frac { { y }^{ 3 } }{ 3 } ] }_{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } } } dx\\ =\frac { 1 }{ 4 } \int _{ 0 }^{ 2 }{ { [{ x }^{ 2 }\sqrt { 2x-{ x }^{ 2 } } +\frac { 1 }{ 3 } { (2x-{ x }^{ 2 }) }^{ \frac { 3 }{ 2 } }] } } dx\\ put\quad x=2\sin ^{ 2 }{ \theta } \Rightarrow dx=4\sin { \theta } \cos { \theta } d\theta
When x=0 then \theta =0 when x=2 then \theta =\frac { \pi }{ 2 }
=\frac { 1 }{ 4 } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \quad } [4\sin ^{ 4 }{ \theta } \sqrt { 4\sin ^{ 2 }{ \theta } -4\sin ^{ 4 }{ \theta } } +\frac { 1 }{ 3 } { (4\sin ^{ 2 }{ \theta } -4\sin ^{ 4 }{ \theta } ) }^{ \frac { 3 }{ 2 } }]4\sin { \theta } \cos { \theta } d\theta \\ =\frac { 1 }{ 4 } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \quad } [4\sin ^{ 4 }{ \theta } (2\sin { \theta } )\sqrt { 1-\sin ^{ 2 }{ \theta } } +\frac { 1 }{ 3 } \times 8\sin ^{ 3 }{ \theta } { (1-\sin ^{ 2 }{ \theta } ) }^{ \frac { 3 }{ 2 } }]4\sin { \theta } \cos { \theta } d\theta \\ =\frac { 1 }{ 4 } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ [8\sin ^{ 5 }{ \theta } \cos { \theta } +\frac { 8 }{ 3 } \sin ^{ 3 }{ \theta } \cos ^{ 3 }{ \theta } ] } 4\sin { \theta } \cos { \theta } d\theta \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ [8\sin ^{ 6 }{ \theta } \cos ^{ 2 }{ \theta } +\frac { 8 }{ 3 } \sin ^{ 4 }{ \theta } \cos ^{ 4 }{ \theta } ] } d\theta \\ =[\frac { 8\Gamma (\frac { 6+1 }{ 2 } )\Gamma (\frac { 2+1 }{ 2 } ) }{ 2\Gamma (\frac { 6+2+2 }{ 2 } ) } +\frac { 8 }{ 3 } \frac { \Gamma (\frac { 4+1 }{ 2 } )\Gamma (\frac { 4+1 }{ 2 } ) }{ 2\Gamma (\frac { 4+4+2 }{ 2 } ) } ]\\ =[4.\frac { \frac { 5 }{ 2 } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } .\frac { 5 }{ 2 } \sqrt { \pi } }{ 2\times 3! } +\frac { 8 }{ 3 } \frac { \frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } }{ 2\times 4! } ]\\ =[4.\frac { \frac { 5 }{ 2 } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } .\frac { 5 }{ 2 } \pi }{ 2\times 3\times 2 } +\frac { 8 }{ 3 } \frac { \frac { 3 }{ 2 } .\frac { 1 }{ 2 } .\frac { 3 }{ 2 } .\frac { 1 }{ 2 } \pi }{ 2\times 4\times 3\times 2\times 1 } ]\\ =[\frac { 5 }{ 32 } \pi +\frac { 1 }{ 32 } \pi ]\\ =\frac { 6 }{ 32 } \pi \\ =\frac { 3 }{ 16 } \pi
Question-4.\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a\sin { \theta } }{ \int _{ 0 }^{ \frac { ({ a }^{ 2 }-{ r }^{ 2 }) }{ a } }{ r } } } d\theta drdz
Solution-\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a\sin { \theta } }{ \int _{ 0 }^{ \frac { ({ a }^{ 2 }-{ r }^{ 2 }) }{ a } }{ r } } } d\theta drdz\\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a\sin { \theta } }{ r{ [z] }_{ 0 }^{ \frac { ({ a }^{ 2 }-{ r }^{ 2 }) }{ a } } } } drd\theta \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a\sin { \theta } }{ \frac { r({ a }^{ 2 }-{ r }^{ 2 }) }{ a } } } drd\theta \\ =\frac { 1 }{ a } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a\sin { \theta } }{ ({ a }r^{ 2 }-{ r }^{ 3 }) } } drd\theta \\ =\frac { 1 }{ a } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { [\frac { { a }^{ 2 }{ r }^{ 2 } }{ 2 } -\frac { { r }^{ 4 } }{ 4 } ] }_{ 0 }^{ a\sin { \theta } } } d\theta \\ =\frac { 1 }{ a } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { [\frac { { a }^{ 2 } }{ 2 } .{ a }^{ 2 }\sin ^{ 2 }{ \theta } -\frac { { a }^{ 4 }\sin ^{ 4 }{ \theta } }{ 4 } ] } } d\theta \\ =\frac { { a }^{ 3 } }{ 2 } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { [\sin ^{ 2 }{ \theta } -\frac { \sin ^{ 4 }{ \theta } }{ 2 } ] } } d\theta \\ =\frac { { a }^{ 3 } }{ 2 } [\frac { \Gamma (\frac { 2+1 }{ 2 } )\Gamma (\frac { 0+1 }{ 2 } ) }{ 2\Gamma (\frac { 2+0+2 }{ 2 } ) } +\frac { 1 }{ 2 } \frac { \Gamma (\frac { 4+1 }{ 2 } )\Gamma (\frac { 0+1 }{ 2 } ) }{ 2\Gamma (\frac { 4+0+2 }{ 2 } ) } ]\\ =\frac { { a }^{ 3 } }{ 2 } [\frac { \frac { 1 }{ 2 } \sqrt { \pi } \sqrt { \pi } }{ 2\times 1 } -\frac { 1 }{ 2 } .\frac { \frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } \sqrt { \pi } }{ 2\times 2 } ]\\ =\frac { { a }^{ 3 } }{ 2 } [\frac { \pi }{ 4 } -\frac { 3\pi }{ 32 } ]\\ =\frac { { a }^{ 3 } }{ 2 } [\frac { 8\pi -3\pi }{ 32 } ]\\ =\frac { { 5\pi a }^{ 3 } }{ 64 }
इस प्रकार उपर्युक्त उदाहरणों के हल द्वारा त्रि समाकलन का मान ज्ञात करने (Evaluation of Triple Integral ) को समझ सकते हैं।
4.ट्रिपल इंटीग्रल का अनुप्रयोग (Application of triple integral)-
(1.)एक समांतर चतुर्भुज [a, b] × [c, d] × [r, s] पर एक फ़ंक्शन f (x, y, z) का ट्रिपल समाकल ,समाकल योग (रीमैन योग) की सीमा के रूप में परिभाषित किया गया है।
(2.)दो फलनों के योग का ट्रिपल समाकल इन फलनों के समाकल के योग के बराबर है।
5.ट्रिपल इंटीग्रल परिभाषा (Triple integral definition)-
त्रि-समाकलन को हम इस फलन के गुणनफल की सीमा के रूप में पारिभाषित कर सकते हैं।द्वि-समाकल, पुनरावृत्त द्वि-समाकल के स्थान पर त्रि-समाकल, पुनरावृत्त त्रि-समाकल के समतुल्य है।
6.ट्रिपल इंटीग्रल वॉल्यूम (Triple integral volume)-
D के आयतन V को ट्रिपल इंटीग्रल द्वारा दर्शाया जाता है, V=∭DdV. द्वारा दर्शाया गया है।\int _{ a }^{ b }{ \int _{ { g }_{ 2 }x }^{ { g }_{ 1 }x }{ \int _{ { f }_{ 2 }(x,y) }^{ { f }_{ 1 }(x,y) }{ dzdydx } } } =\int _{ a }^{ b }{ \int _{ { g }_{ 2 }x }^{ { g }_{ 1 }x }{ (\int _{ { f }_{ 2 }(x,y) }^{ { f }_{ 1 }(x,y) }{ dz } )dydx } } ।उपरोक्त पुनरावृत्त समाकल का मूल्यांकन ट्रिपल समाकलन है।
Also Read This Article:-Length of plane curves (Rectification)
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |