SA of Solids of Revolution
1.परिक्रमण ठोसों का पृष्ठीय क्षेत्रफल (SA of Solids of Revolution),परिक्रमण ठोस का पृष्ठीय क्षेत्रफल (Surface Area of Solid of Revolution):
- परिक्रमण ठोसों का वक्र पृष्ठीय क्षेत्रफल (SA of Solids of Revolution) किसी चाप अथवा वक्र द्वारा अक्षों के परित: अतवा किसी रेखा के सापेक्ष परिक्रमण से जनित होता है।यहाँ पृष्ठीय क्षेत्रफल से तात्पर्य घेरे गए पृष्ठीय क्षेत्रफल से है क्योंकि किसी चाप द्वारा पृष्ठ ही जनित होता है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Surface Area of Solid of Revolution
2.परिक्रमण ठोसों का पृष्ठीय क्षेत्रफल के साधित उदाहरण (SA of Solids of Revolution Solved Examples):
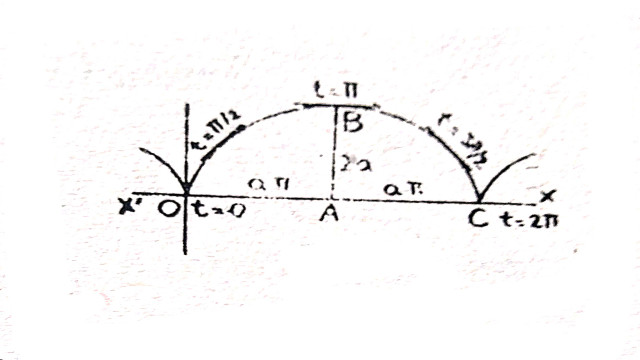
Example:1.प्रदर्शित कीजिए कि साइक्लाॅइड x=a\left({\theta}-\sin{\theta}\right),y=a\left(1-\cos{\theta}\right) को रेखा y=0 के सापेक्ष घुमाने से जनित पृष्ठ क्षेत्रफल है।
(Show that the area of the surface generated by the revolution of the cycloid x=a\left({\theta}-\sin{\theta}\right),y=a\left(1-\cos{\theta}\right) about the line y=0 is.)
Solution:साइक्लाॅइड का समीकरण:x=a\left({\theta}-\sin{\theta}\right),y=a\left(1-\cos{\theta}\right)
{\theta} के सापेक्ष अवकलन करने पर:
\frac{dx}{d\theta}=a\left(1-\cos{\theta}\right)
\frac{dy}{d\theta}=a\sin{\theta}
\frac{ds}{d\theta}=\sqrt{\left(\frac{dx}{d\theta}\right)^{2}+\left(\frac{dy}{d\theta}\right)^{2}}
=\sqrt{a^{2}\left(1-\cos{\theta}\right)^{2}+\left(a\sin{\theta}\right)^{2}}
=\sqrt{a^{2}\left(1-2\cos{\theta}+\cos^{2}{\theta}\right)+a^{2}\sin^{2}{\theta}}
=a\sqrt{1-2\cos{\theta}+cos^{2}{\theta}+\sin^{2}{\theta}}
=a\sqrt{1+1-2\cos{\theta}}
=a\sqrt{2-2\cos{\theta}}
\sqrt{2}a\sqrt{1-\cos{\theta}}
अभीष्ट पृष्ठीय क्षेत्रफल=
=2 × \int_{{\theta}=0}^{\pi}2{\pi}y ds
=4{\pi}\int_{0}^{\pi}y\left(\frac{ds}{d\theta}\right).{d\theta}
=4{\pi}\int_{0}^{\pi}a\left(1-\cos{\theta}\right).\sqrt{2}a\sqrt{1-\cos{\theta}}{d\theta}
=4\sqrt{2}{\pi}a^{2}\int_{0}^{\pi}\left(2\sin^{2}{\frac{\theta}{2}}\right)^{\frac{3}{2}}{d\theta}
=16{\pi}a^{2}\int_{0}^{\pi}\sin^{3}{\frac{\theta}{2}}{d\theta}
\text{ Put }{\frac{\theta}{2}}={\phi}
\Rightarrow{d\theta}=2{d\phi}
\text{ जब }{\theta}=0 \text{ तो }{\phi}=0
\text{ जब }{\theta}={\pi} \text{ तो }{\phi}={\frac{\pi}{2}}
=16{\pi}a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{3}{\phi}.{2d\phi}
=32{\pi}a^{2}\frac{\Gamma{\left(\frac{3+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{3+0+2}{2}\right)}}
=32{\pi}a^{2}\frac{\sqrt{\pi}}{2.\frac{3}{2}.\frac{1}{2}\sqrt{\pi}}
\frac{64}{3}{\pi}a^{2}
Example:2.कार्डिआइड r=a\left(1-\cos{\theta}\right) को प्रारम्भिक रेखा के सापेक्ष घुमाने से बने ठोस का पृष्ठ ज्ञात कीजिए।
(Find the surface of the solid obtained by revolving the cardiod r=a\left(1-\cos{\theta}\right) about its initial line.)
Solution:कार्डिआइड की समीकरण:r=a\left(1-\cos{\theta}\right)
{\theta} के सापेक्ष अवकलन करने पर:
\frac{dr}{d\theta}=a\sin{\theta}
\frac{ds}{d\theta}=\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}
=\sqrt{a^{2}\left(1-\cos{\theta}\right)^{2}+a^{2}\sin^{2}{\theta}}
=a\sqrt{1-2\cos{\theta}+\cos^{2}{\theta}+sin^{2}{\theta}}
=a\sqrt{2-2\cos{\theta}}
=\sqrt{2}a\sqrt{1-\cos{\theta}}
अभीष्ट पृष्ठीय क्षेत्रफल=\int_{\alpha}^{\beta}2{\pi}r\sin{\theta} ds
=\int_{0}^{\pi}2{\pi}r\sin{\theta}\frac{ds}{d\theta}{d\theta}
=2{\pi}\int_{0}^{\pi}a\left(1-\cos{\theta}\right)\sin{\theta}.\sqrt{2}a\sqrt{1-\cos{\theta}}{d\theta}
=2\sqrt{2}{\pi}a^{2}\int_{0}^{\pi}\left(1-\cos{\theta}\right)^{\frac{3}{2}}\sin{\theta}{d\theta}
=2\sqrt{2}{\pi}a^{2}\int_{0}^{\pi}\left(2\sin^{2}{\theta}\right)^{\frac{3}{2}}2\sin{\frac{\theta}{2}}\cos{\frac{\theta}{2}}{d\theta}
=2\sqrt{2}{\pi}a^{2}\int_{0}^{\pi}2\sqrt{2}\sin^{3}{\frac{\theta}{2}}2\sin{\frac{\theta}{2}}\cos{\frac{\theta}{2}}{d\theta}
=16{\pi}a^{2}\int_{0}^{\pi}\sin^{4}{\frac{\theta}{2}}\cos{\frac{\theta}{2}}{d\theta}
\text{ Put }{\frac{\theta}{2}}={\phi}
\Rightarrow{d\theta}=2{d\phi}
\text{ जब }{\theta}=0 \text{ तो }{\phi}=0
\text{ जब }{\theta}={\pi} \text{ तो }{\phi}={\frac{\pi}{2}}
=32{\pi}a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{4}{\phi}\cos{\phi}
=32{\pi}a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{1+2}{2}\right)}}{2\Gamma{\left(\frac{4+1+2}{2}\right)}}
=32{\pi}a^{2}\frac{\frac{3}{2}\frac{1}{2}\sqrt{\pi}}{2 × \frac{5}{2}.\frac{3}{2}.\frac{1}{2}.\sqrt{\pi}}
=\frac{32}{5}{\pi}a^{2}
Example:3.वक्र r=2a\cos{\theta} को प्रारम्भिक रेखा के सापेक्ष घुमाने से जनित ठोस के पृष्ठ का क्षेत्रफल ज्ञात कीजिए।
(Find the area of the surface generated by revolving the curve r=2a\cos{\theta} about the initial line.)
Solution:वक्र का समीकरण:r=2a\cos{\theta}
{\theta} के सापेक्ष अवकलन करने पर:
\frac{dr}{d\theta}=-2a\sin{\theta}
\frac{ds}{d\theta}=\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}
=\sqrt{\left(2a\cos{\theta}\right)^{2}+\left(-2a\sin{\theta}\right)^{2}}
=\sqrt{4a^{2}\cos^{2}{\theta}+4a^{2}\sin^{2}{\theta}}
=\sqrt{4a^{2}\left(\cos^{2}{\theta}+\sin^{2}{\theta}\right)}
\Rightarrow \frac{ds}{d\theta}=2a
अभीष्ट पृष्ठीय क्षेत्रफल=\int_{\alpha}^{\beta}2{\pi}r\sin{\theta} ds
=
=\int_{\alpha}^{\beta}2{\pi}r\sin{\theta}\frac{ds}{d\theta}{d\theta}
=\int_{0}^{\frac{\pi}{2}}2{\pi}.2a\cos{\theta}.\sin{\theta}.2a{d\theta}
=\int_{0}^{\frac{\pi}{2}}8{\pi}.a^{2}\cos{\theta}\sin{\theta}{d\theta}
=8{\pi}.a^{2}\left[\frac{\sin^{2}{\theta}}{2}\right]_{0}^{\frac{\pi}{2}}
=4{\pi}.a^{2}
Example:4.लैमनिस्केट r^{2}=a^{2}\cos{2\theta} को प्रारम्भिक रेखा के सापेक्ष घुमाने से बने ठोस का पृष्ठ ज्ञात कीजिए। (Find the surface of the solid formed by the revolution of the lemniscate r^{2}=a^{2}\cos{2\theta} about the initial line.)
Solution:लैमनिस्केट का समीकरण:[kayex]r^{2}=a^{2}\cos{2\theta}[/katex]
{\theta} के सापेक्ष अवकलन करने पर:
2r\frac{dr}{d\theta}=-2a^{2}\sin{2\theta}\\
\Rightarrow \frac{dr}{d\theta}=-\frac{a^{2}\sin{2\theta}}{r}\\
\frac{ds}{d\theta}=\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}
=\sqrt{r^{2}+\left(-\frac{a^{2}\sin{2\theta}}{r}\right)^{2}}
=\sqrt{r^{2}+\frac{a^{4}sin^{2}{2\theta}}{r^{2}}}
=\sqrt{a^{2}\cos{2\theta}+\frac{a^{2}sin^{2}{2\theta}}{\cos{2\theta}}}\\ =a\sqrt{\frac{\cos^{2}{2\theta}+\sin^{2}{2\theta}}{\cos{2\theta}}}
=a\sqrt{\frac{1}{\cos{2\theta}}}
=\frac{a}{\sqrt{\cos{2\theta}}}
अभीष्ट वक्र पृष्ठीय क्षेत्रफल=
=2 × \int_{\alpha}^{\beta}2{\pi}r\sin{\theta} ds
=2 × \int_{\alpha}^{\beta}2{\pi}r\sin{\theta}\frac{ds}{d\theta}{d\theta}
4{\pi}\int_{0}^{\frac{\pi}{4}}r\sin{\theta}.\frac{a}{\sqrt{\cos{2\theta}}}{d\theta}
[\because y=r\sin{\theta}]
4{\pi}a\int_{0}^{\frac{\pi}{4}}a\sqrt{\cos{2\theta}}\sin{\theta}.\frac{1}{\sqrt{\cos{2\theta}}}{d\theta}
=4{\pi}a^{2}\int_{0}^{\frac{\pi}{4}}\sin{\theta}{d\theta}
=4{\pi}a^{2}\left[-\cos{\theta}\right]_{0}^{\frac{\pi}{4}}
=4{\pi}a^{2}\left[-\cos{\frac{\pi}{4}}+\cos{0}\right]
=4{\pi}a^{2}\left(1-\frac{1}{\sqrt{2}}\right)
Example:5.-\frac{1}{2}{\pi}\leq {\theta}\leq{\frac{1}{2}} के अन्तर्गत कार्डिआइड r=a\left(1+\cos{\theta}\right) के चाप को रेखा {\theta}=\frac{1}{2}{\pi} के सापेक्ष घुमाया जाता है।इस प्रकार जनित पृष्ठ का क्षेत्रफल ज्ञात कीजिए। (The arc of the cardioid
r=a\left(1+\cos{\theta}\right) included between -\frac{1}{2}{\pi}\leq {\theta}\leq{\frac{1}{2}} is rotated about the line {\theta}=\frac{1}{2}{\pi}.Find the area of the surface generated.) Solution:कार्डिआइड की समीकरण:r=a\left(1+\cos{\theta}\right)
{\theta} के सापेक्ष अवकलन करने पर:
\frac{dr}{d\theta}=-a\sin{\theta}
\frac{ds}{d\theta}=\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}
=\sqrt{a^{2}\left(1+\cos{\theta}\right)^{2}+a^{2}\sin^{2}{\theta}}
=a\sqrt{1+2\cos{\theta}+\cos^{2}{\theta}+sin^{2}{\theta}}
=a\sqrt{2+2\cos{\theta}} =\sqrt{2}a\sqrt{1+\cos{\theta}}
अभीष्ट पृष्ठीय क्षेत्रफल=
\int_{\alpha}^{\beta}2{\pi}y ds
\int_{\alpha}^{\beta}2{\pi}r\sin{\theta} ds
=\int_{0}^{\frac{\pi}{2}}r\sin{\theta}\frac{ds}{d\theta}{d\theta}
=2{\pi}\int_{0}^{\frac{\pi}{2}}a\left(1+\cos{\theta}\right)\sin{\theta}.\sqrt{2}a\sqrt{1+\cos{\theta}}{d\theta}
=2\sqrt{2}{\pi}a^{2}\int_{0}^{\frac{\pi}{2}}\left(1+\cos{\theta}\right)^{\frac{3}{2}}\sin{\theta}{d\theta}
\text{ Put }1+\cos{\theta}=t
\Rightarrow -\sin{\theta}{d\theta}=dt
\text{ जब }{\theta}=0 \text{ तो }t=2
\text{ जब }{\theta}=\frac{\pi}{2} \text{ तो }t=1
=2\sqrt{2}{\pi}a^{2}\int_{2}^{1}\left(-t^{\frac{3}{2}}\right)dt
=2\sqrt{2}{\pi}a^{2}\int_{1}^{2}\left(t^{\frac{3}{2}}\right)dt
=2\sqrt{2}{\pi}a^{2}\left[\frac{2}{5}t^{\frac{5}{2}}\right]_{1}^{2}
=2\sqrt{2}{\pi}a^{2}\left[\frac{2}{5}2^{\frac{5}{2}}-\frac{2}{5}\right] =\frac{4\sqrt{2}{\pi}a^{2}}{5}\left[2^{\frac{5}{2}}-1\right]
=\frac{4\sqrt{2}{\pi}a^{2}}{5}\left[4\sqrt{2}-1\right]
=\frac{4{\pi}a^{2}}{5}\left[8-\sqrt{2}\right]
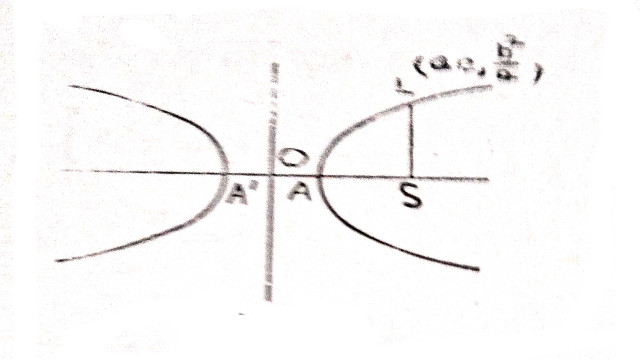
Example:6.समकोणीय अतिपरवलय x^{2}-y^{2}=a^{2} के शीर्ष से नाभिलम्ब के एक सिरे तक चाप को x-अक्ष के सापेक्ष चार समकोण घुमाने से बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (Find the area of the surface swept out by the arc of the rectangle hyperbola x^{2}-y^{2}=a^{2}, extending from the vertex to the end of the latus rectum, when roated through four right angles about the axis of x.)
Solution:अतिपरवलय \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 के लिए A(a,0) तथा L\left(ae,\frac{b^{2}}{a}\right) है। तथा b^{2}=a^{2}\left(e^{1}-1\right) दिए हुए अतिपरवलय में b=a
a^{2}=a^{2}\left(e^{1}-1\right)
\Rightarrow e^{2}=2
\Rightarrow e=\pm{\sqrt{2}}
अतः L\left(\sqrt{2}a,a\right) है।
अतिपरवलय की समीकरण:x^{2}-y^{2}=a^{2}
x के सापेक्ष अवकलन करने पर:
2x-2y\frac{dy}{dx}=0\\
\Rightarrow \frac{dy}{dx}=\frac{x}{y}\\
\frac{ds}{dx}=\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}
=\sqrt{1+\frac{x^{2}}{y^{2}}}
=\sqrt{\frac{x^{2}+y^{2}}{y^{2}}}
=\frac{\sqrt{x^{2}+x^{2}-a^{2}}}{y} =\frac{\sqrt{2x^{2}-a^{2}}}{y}
\frac{\sqrt{2}\sqrt{x^{2}-\left(\frac{a}{2}\right)^{2}}}{y}
अभीष्ट पृष्ठीय क्षेत्रफल=
\int_{a}^{\sqrt{2}a}2{\pi}y\frac{ds}{dx}.dx
=\int_{a}^{\sqrt{2}a}2{\pi}y\frac{\sqrt{2}\sqrt{x^{2}-\left(\frac{a}{2}\right)^{2}}}{y} dx
=2\sqrt{2}{\pi}\int_{a}^{\sqrt{2}a}\sqrt{x^{2}-\left(\frac{a}{2}\right)^{2}} dx
=2\sqrt{2}{\pi}[\frac{x}{2}\sqrt{\left(x^{2}-\frac{a^{2}}{2}\right)}-\frac{a^{2}}{4}\log{\left\{x+\sqrt{x^{2}-\frac{a^{2}}{2}}\right\}]_{a}^{\sqrt{2}a}}
=2\sqrt{2}{\pi}[\frac{a}{\sqrt{2}}\sqrt{\frac{3}{2}}a-\frac{a^{2}}{4}\log{\left\{\sqrt{2}a+\sqrt{\frac{3}{2}}a\right\}}\\-\frac{a}{2}\sqrt{a^{2}-\frac{a^{2}}{2}}+\frac{a^{2}}{4}\log{\left\{a+\frac{1}{\sqrt{2}a}\right\}}]
=2\sqrt{2}{\pi}[\frac{\sqrt{3}}{2}a^{2}-\frac{a^{2}}{2\sqrt{2}}+\frac{a^{2}}{4}\log{\left\{\frac{a+\frac{1}{\sqrt{2}}a}{\sqrt{2}a+\sqrt{\frac{3}{2}}a}\right\}}]
=\frac{2\sqrt{2}}{2\sqrt{2}}{\pi}a^{2}[\sqrt{6}-1+\frac{1}{\sqrt{2}}\log{\left(\frac{\sqrt{2}+1}{2+\sqrt{3}}\right)}]
={\pi}a^{2}[\sqrt{6}-1+\frac{1}{\sqrt{2}}\log{\left(\frac{\sqrt{2}+1}{2+\sqrt{3}}\right)}]
उपर्युक्त उदाहरणों के द्वारा परिक्रमण ठोसों का पृष्ठीय क्षेत्रफल (SA of Solids of Revolution),परिक्रमण ठोस का वक्र पृष्ठीय क्षेत्रफल (Surface Area of Solid of Revolution) को समझ सकते हैं।
Also Read This Article:Volume of Solid of Revolution Examples
3.परिक्रमण ठोसों का पृष्ठीय क्षेत्रफल (CSA of Solids og Revolution),परिक्रमण ठोस का पृष्ठीय क्षेत्रफल (Surface Area of Solid of Revolution) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.गामा फलन के मुख्य सूत्र लिखो।(Write the main formula of the gamma function):
उत्तर:गामा फलन के मुख्य निम्न हैं: (1.)\Gamma{\left(n+1\right)=n\Gamma{n}}
(2.)\Gamma{\left(1\right)}=1
(3.)\Gamma{\left(n+1\right)}=n!
(4.)\Gamma{\left(\frac{1}{2}\right)}=\sqrt{\pi}
(5.)\int_{0}^{\frac{\pi}{2}}\sin^{m}{x}\cos^{n}{x} dx=\frac{\Gamma{\left(\frac{m+1}{2}\right)}\Gamma{\left(\frac{n+1}{2}\right)}}{2\Gamma{\left(\frac{m+n+2}{2}\right)}}
प्रश्न:2.पृष्ठ को परिभाषित करो।(Define Surface):
उत्तर:पृष्ठ वह ज्यामितीय आकृति है जिसके बिन्दुओं के निर्देशांक Z=f(x,y) या F(x,y,z)=0 जैसे समीकरण अथवा x=X(u,v),y=Y(u,v),z=Z(u,v) जैसे प्राचलिक समीकरण को सन्तुष्ट करते हैं।उदाहरणार्थ x^{2}+y^{2}+z^{2}=4 उस गोले के पृष्ठ का समीकरण जिसकी त्रिज्या 2 है और जिसका केन्द्र (0,0,0) पर है।
प्रश्न:3.प्रारम्भिक रेखा किसे कहते हैं? (What is the initial line called?):
उत्तर:यदि वक्र का समीकरण ध्रुवीय रूप में अर्थात् r=f\left({\theta}\right)हो तो x-अक्ष (भुज) को प्रारम्भिक रेखा (initial line) कहा जाता हैं।
प्रश्न:4.परिक्रमण ठोसों के पृष्ठीय क्षेत्रफल के सूत्र लिखो।(Write the formulas for the surface area of the solids of revolution ):
उत्तर:परिक्रमण ठोसों की भिन्न-भिन्न स्थितियों के लिए अलग-अलग सूत्र हैं।ये भिन्न-भिन्न स्थितियों के सूत्र निम्न हैं:
(1.)x-अक्ष के सापेक्ष परिक्रमण से जनित ठोस का पृष्ठीय क्षेत्रफल=\int_{a}^{b}2{\pi}y dx
ds=\sqrt{1+\left(\frac{dy}{dx}\right)^{2}} dx
(2.)y-अक्ष के सापेक्ष परिक्रमण से जनित ठोस का पृष्ठीय क्षेत्रफल=\int_{c}^{d}2{\pi}y dx
(3.)यदि वक्र का समीकरण ध्रुवीय रूप में हो तो वक्र को प्रारम्भिक (Initial line) के सापेक्ष परिक्रमण से जनित ठोस का पृष्ठीय क्षेत्रफल=
\int_{\alpha}^{\beta}2{\pi}r\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}{d\theta}
(4.)यदि वक्र का समीकरण प्राचलिक रूप में हो तथा वक्र x-अक्ष के सापेक्ष परिक्रमण करें तो जनित ठोस का पृष्ठीय क्षेत्रफल=
\int_{{t}_{1}}^{{t}_{2}}2{\pi}y\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}dt
(5.)यदि वक्र AB रेखा OE के सापेक्ष परिक्रमण करता है तो जनित ठोस का पृष्ठीय क्षेत्रफल=
\int_{\text{OC}}^{\text{OD}}2{\pi}\left(\text{PL}\right)ds
- उपर्युक्त प्रश्नों के उत्तर द्वारा परिक्रमण ठोसों का पृष्ठीय क्षेत्रफल (SA of Solids of Revolution),परिक्रमण ठोस का वक्र पृष्ठीय क्षेत्रफल (Surface Area of Solid of Revolution) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
SA of Solids of Revolution
परिक्रमण ठोसों का पृष्ठीय क्षेत्रफल
(SA of Solids of Revolution)
SA of Solids of Revolution
परिक्रमण ठोसों का वक्र पृष्ठीय क्षेत्रफल (SA of Solids of Revolution) किसी चाप अथवा वक्र द्वारा अक्षों के
परित: अतवा किसी रेखा के सापेक्ष परिक्रमण से जनित होता है।यहाँ पृष्ठीय क्षेत्रफल से
तात्पर्य घेरे गए पृष्ठीय क्षेत्रफल से है क्योंकि किसी चाप द्वारा पृष्ठ ही जनित होता है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |