Mathematician Rene Descartes
1.गणितज्ञ रेने देकार्त (Mathematician Rene Descartes),रेने देकार्त (Rene Descartes):
- गणितज्ञ रेने देकार्त (Mathematician Rene Descartes) का जन्म 31 मार्च सन् 1596 ईस्वी को फ्रांस के तुरेन नामक स्थान में सन् 1596 ईस्वी में हुआ।उनके पिता धनाढ्य थे।रेने देकार्त बहुत कमजोर बालक थे।उनके पिता चाहते थे कि उनका पुत्र आराम का जीवन व्यतीत करें।उनकी औपचारिक शिक्षा 8 वर्ष की आयु में प्रारंभ हुई। उनकी शिक्षा-दीक्षा ईसाई धर्म में हुई।शीरीरिक दृष्टि से कमजोर होने के कारण वे अपने बिस्तर के ही इर्द-गिर्द सुबह का समय व्यतीत करते थे।जब चिन्तन करते थे तो बिस्तर में लेटे-लेटे करते थे।
- पैतृक सम्पत्ति प्रचुर मात्रा में होने की वजह से बिना किसी नौकरी या पेशे के ही देकार्त ने स्वतंत्र जीवन निर्वाह किया।रेने देकार्त फ्रांसीसी दार्शनिक,मनोवैज्ञानिक,रसायनज्ञ,भौतिकविद्,ब्रह्मांड विज्ञानी एवं शरीर विज्ञान विज्ञानी भी थे।इन ज्ञान-शास्त्रों में भी समान अधिकार रखते थे।
- एक सुबह उनके जीवन में महत्त्वपूर्ण घटना हुई। उस सुबह उन्होंने विश्लेषणात्मक ज्यामिति (Analytical Geometry) की खोज की।अपने बिस्तर पर लेटे हुए उनकी आंखें एक मक्खी पर टिकी।उन्होंने देखा कि वह कमरे की छत पर रेंग रही थी।उनके मस्तिष्क में एक गणितीय समस्या उभरी:”इस मक्खी के रेंगने के मार्ग का गणितीय भाषा में विवरण देना” इस समस्या ने उनके मस्तिष्क में विश्लेषणात्मक ज्यामिति को जन्म दिया।
- देकार्त अपने समय के सुविख्यात गणितज्ञ थे और यही कारण है कि रचना करने में वे गणितीय विधि से बहुत प्रभावित हुए।गणित में सबसे पहले स्वयंसिद्धों की स्थापना की जाती है और तब उसके आधार पर निगमनात्मक रीति से अन्य निष्कर्ष स्थापित किए जाते हैं।देकार्त ने दर्शन में भी असाक्षात रूप से इसी प्रणाली का अनुकरण किया है।रेने देकार्त को आधुनिक गणित का पिता कहा जाता है।
- बुद्धिवाद,विज्ञानवाद इत्यादि देकार्त की मुख्य देन है।देकार्त उस युग में हुए थे जिसमें धार्मिक संस्था की प्रभुता विशेष थी और उसे छोड़कर बुद्धि के आधार पर सत्यता की स्थापना करने का प्रयास तो उनकी निर्भीकता तथा स्वतंत्रता का ठोस प्रमाण है। इसका परिणाम यह हुआ कि धीरे-धीरे विचारक स्वतंत्र होने लगे और अंधविश्वास तथा निरर्थक पुरानी लीकों को छोड़कर नई दिशा में प्रगति करने लग गए।विचार स्वातन्त्र्य के पक्ष को स्वीकार करने के कारण देकार्त की विधि ने दार्शनिकों के लिए मैग्नाकार्टा का अधिकार सुलभ कर दिया है।
- परंतु सही मायने में देकार्त का महत्त्व गणितीय विधि को अपनाने में है।गणित का वह सिद्धांत है जिसके अनुसार गणित की पद्धति तथा खोजें किसी भी ज्ञान की एकमात्र पद्धति तथा सत्यता की कसौटी है।चूँकि देकार्त के समय में और खासकर उनके लिए गणित ही विज्ञान का विशेष अंग था इसलिए उन्होंने दर्शन में गणित की परंपरा को चलाने की कोशिश की है और इस परंपरा को प्राय: सभी आधुनिक दार्शनिकों ने अपनाया है।अब गणित की अपनी कुछ विशेषताएं हैं जिनका स्थान स्पिनोजा,कांट इत्यादि के दर्शन में मिलेगा।गणित विज्ञानों में महत्त्वपूर्ण स्थान रखता है और इसलिए आगे चलकर गणितवाद और वैज्ञानिकवाद में बदल गया।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Crown of Greek Mathematics Edoxus
(1.)रेने देकार्त गणितज्ञ योगदान (Rene Descartes Mathematician Contribution):
- यूक्लिड की ज्यामिति के बारे में प्रमुख बात यह है कि इसकी सारी आकृतियां एक समतल पर खींची जाती है।दूसरी बात यह है कि इस ज्यामिति की आकृतियों के कोणों तथा रेखाओं को मापना पड़ता है अर्थात् यूक्लिड की ज्यामिति एक मापीय ज्यामिति है।इस ज्यामिति में लंबाईयाँ नहीं,कोण नहीं बदलते।
- परंतु ऐसी ज्यामितियाँ भी है जिनमें कोण तथा लम्बाईयाँ बदल जाती है।यदि किसी वस्तु का चित्र तैयार किया जाए या फोटो उतारा जाए तो इनमें मूलवस्तु के कोण तथा इसकी लंबाईयाँ बदल जाती है।ज्यामिति को प्रक्षेप ज्यामिति कहते हैं।फ्रांस के दो गणितज्ञ देकार्त (1593-1662) तथा पास्कल (1623-62) इस ज्यामिति के संस्थापक माने जाते हैं।यूरोप के चित्रकारों ने प्रक्षेप-ज्यामिति के विकास में खूब योग दिया।
- देकार्त ने एक बहुत ही उपयोगी नई ज्यामिति को जन्म दिया।इस ज्यामिति को निर्देशांक ज्यामिति (कोर्डिनेट ज्योमेट्री) का नाम दिया गया है।इस ज्यामिति की कुछ बातों को आगे की आकृतियों से समझा जा सकता है।
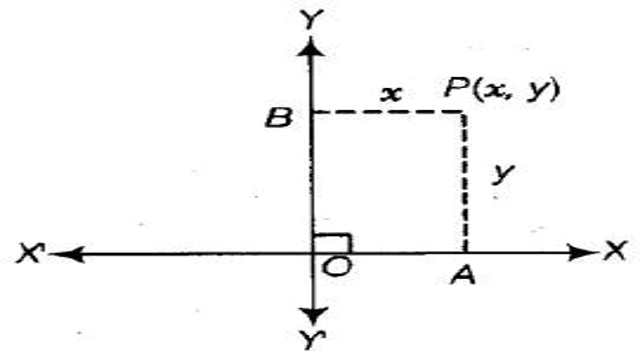
- प्रथम आकृति में समतल पर एक-दूसरे को समकोण में काटती हुई दो सीधी रेखाएं हैं।इन रेखाओं को निर्देश-रेखाएं कहते हैं।अब मान लो कि इन निर्देश-रेखाओं के समतल में कोई वक्र है और इस वक्र पर p(x,y) एक बिंदु है।तब y-अक्ष से p बिंदु की दूरी होगी x और x-अक्ष से इसकी दूरी होगी y।इसलिए समतल में p बिंदु की स्थिति को दो निर्देशांको x तथा y से व्यक्त किया जाता है और इसे p(x,y) लिखा जाता है।इस प्रकार किसी भी बिंदु या वक्र की स्थिति को निर्देशांकों में व्यक्त किया जा सकता है।
- एक उदाहरण से इस बात को ओर आसानी से समझा जा सकता है:निम्न आकृति में निर्देश-रेखाओं के काट-बिंदु पर एक वृत्त का केंद्र स्थित है।हम जानते हैं की परिधि के सभी बिंदु वृत्त के केंद्र से समान दूरी पर होते हैं।आकृति में परिधि के किसी भी बिंदु के निर्देशांक होंगे R(a,b) और परिधि पर किसी भी बिंदु की केंद्र से दूरी होगी OR।
- अब यह एक समकोण त्रिभुज है।तब शुल्व प्रमेय (पाइथागोरस प्रमेय) के अनुसार:
OR^2=a^2+b^2 - परिधि पर कोई भी बिंदु लिया जाए तो हमें वृत्त के लिए यही समीकरण प्राप्त होगा।
OR^2=a^2+b^2 क्या है?यह तीन राशियों के बीच एक संबंध है।यदि निर्देशांक मान संख्या में दिए जाएं तो हम वृत्त के आकार को जान सकते हैं।वास्तव में OR^2=a^2+b^2 व्यापक रूप से वृत्त का समीकरण है। - यदि वृत्त की आकृति न भी दी गई हो केवल समीकरण ही दिया गया हो तो इससे हम वृत्त के बारे में सभी बातें जान सकते हैं।
इसी प्रकार सभी वक्रों के लिए समीकरण प्राप्त किए जा सकते हैं और इनसे उनका अध्ययन किया जा सकता है।इसलिए इस ज्यामिति को वैश्लेषिक ज्यामिति (एनेलिटिकल ज्योमेट्री) भी कहते हैं। समतल पर खींचे गए वक्रों तथा आकृतियों के लिए केवल दो निर्देशांकों की आवश्यकता होती है।परंतु हमारे दैनिक जीवन का संसार तीन आयामों (विमितियों) का है।इसलिए ठोस वस्तुओं की ज्यामिति के लिए तीन निर्देशांकों की जरूरत पड़ती है।इस प्रकार की ज्यामिति भी है और यह उच्च कक्षाओं में पढ़ाई जाती है।परंतु अभी ज्यामितियों का सिलसिला समाप्त नहीं हुआ है।यूक्लिड के सिद्धांतों के विरोध में भी कई ज्यामितियों का निर्माण हुआ है।इन्हें अ-यूक्लिडीय ज्यामितियों का नाम दिया गया है। - ला ज्योमेट्री (La Geometric) गणित को देकार्त की प्रमुख देन है।सार रूप में इसके महत्त्व को स्काॅट (Scot) ने चार बिंदुओं में इस प्रकार प्रस्तुत किया है:
- (1.)इनवेरिएण्ट्स के सिद्धांत पर प्रथम पत्र (He make the first step towards the theory of invariants,which of later stages deretativises the system of reference and removes arbitrariness)
- (2.)बीजगणित और ज्यामिति को अन्तर्सम्बन्धित किया (Algebra makes it possible to recognise the typical problems in geometry and to bring together problems which in geometrical dress would not appear to be related at all.)
- (3.)बीजगणित को ज्यामिति को देन (Algebra inports into geometry the most natural principales of division and most natural hierarchy of method.)
- (4.)सॉल्वेबिलिटी संबंधी (No long can question of solvability and geometrical possibility be decided elegantly, quickly and fully from the parallel algebra,without it they cannot be decided at all.)
इनकी प्रमुख रचनाएं इस प्रकार: - (1.) Meditations on first philosophy (1641)
- (2.)I Principia philosophical (1644).
चार भागों में I Principles of human knowledge, II Principles of material things, III of the visible world.IV the earth - ख्याति प्राप्त गणितज्ञ और दार्शनिक होने के कारण स्वीडन की रानी क्रिस्टीना (Queen Christina) ने इनसे शिक्षा ग्रहण करने के लिए इन्हें आमंत्रित किया।ये सन् 1649 ईस्वी में वहां गए।यही उनको अपने स्वभाव के विपरीत 11:00 बजे जागने के बजाय 5:00 बजे प्रातः जागना पड़ा।ऐसे में वहां की ठंड को सहन नहीं कर सके।अतः निमोनिया से पीड़ित होकर 11 फरवरी 1650 को उनका देहांत हो गया।
- उपर्युक्त आर्टिकल में गणितज्ञ रेने देकार्त (Mathematician Rene Descartes),रेने देकार्त (Rene Descartes) के बारे में बताया गया है।
Also Read This Article:Mathematician Sridharacharya
हास्य-व्यंग्य (Humor-Satire):
मॉं (मोहन से):तुम्हारी रिपोर्ट कार्ड में इस बार इतने कम नम्बर कैसे आए हैं?
मोहन:मॉ,आप ही तो हमेशा कह्ती हो कि आदमी को थोड़े मे संतोष करना चाहिए.
नसीहत:चाण्क्य नीति में कहा है कि:
“संतोषस्त्रिषु कर्तव्य:स्वदारे भोजने धने.
त्रिषु चैव न कर्तव्योअध्ययने तपदानयो:.”
अर्थात अपनी पत्नी,भोजन और धन इन तीन में संतोष रखना चाहिए परंतु अध्ययन,तप और ज्ञान इन तीनों में कभी संतोष न्हीं करना चाहिए.
2.गणितज्ञ रेने देकार्त (Mathematician Rene Descartes),रेने देकार्त (Rene Descartes) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.देकार्त के लिए सबसे प्रसिद्ध क्या है? (What is Descartes most famous for?):
उत्तर:देकार्त को पहले आधुनिक दार्शनिक के रूप में शुरुआत की गई है।वह ज्यामिति (Geometry) और बीजगणित (Algebra) के बीच एक महत्वपूर्ण संबंध बनाने के लिए प्रसिद्ध है,जिसने बीजीय समीकरणों के माध्यम से ज्यामितीय समस्याओं को हल करने की अनुमति दी।
प्रश्न:2.रेने देकार्त सिद्धांत क्या था? (What was René Descartes theory?):
उत्तर:देकार्त ने जन्मजात ज्ञान (innate knowledge) के सिद्धांत का तर्क दिया और कहा कि सभी मनुष्य परमेश्वर की उच्च शक्ति के माध्यम से ज्ञान के साथ पैदा हुए थे।यह जन्मजात ज्ञान का यह सिद्धांत था जिसका बाद में दार्शनिक जॉन लाॅक (John Locke) (1632-1704),एक अनुभवजन्य द्वारा मुकाबला किया गया था। अनुभववाद (Empiricism) मानती है कि सभी ज्ञान अनुभव (experience) के माध्यम से प्राप्त किया जाता है।
प्रश्न:3.देकार्त मुख्य विचार क्या थे? (What were Descartes main ideas?):
उत्तर:विद्वानों का मानना है कि देकार्त कम से कम तीन जन्मजात विचारों (innate ideas) को पहचानता है:परमेश्वर का विचार (idea of God) मन का विचार (परिमित (finite)) (the idea of mind) और शरीर का विचार (अनिश्चित) (the idea of body)।
प्रश्न:4.रेने देकार्त का योगदान क्या है? (What is the contribution of Rene Descartes?):
उत्तर:रेने देकार्त ने विश्लेषणात्मक ज्यामिति (Analytical Geometry) का आविष्कार किया और वैज्ञानिक विधि के एक अनिवार्य हिस्से के रूप में संदेह (skepticism) पेश किया।उन्हें इतिहास के महानतम दार्शनिकों में से एक माना जाता है।उनकी विश्लेषणात्मक ज्यामिति एक जबरदस्त वैचारिक सफलता थी,जो ज्यामिति और बीजगणित के पहले अलग क्षेत्रों को जोड़ती थी।
प्रश्न:5.देकार्त ने दुनिया को कैसे बदल दिया? (How did Descartes change the world?):
उत्तर:रेने देकार्त को आम तौर पर आधुनिक दर्शन का पिता (father of modern philosophy) माना जाता है।वह दार्शनिक आंदोलन में पहला प्रमुख हस्ती था जिसे तर्कवाद (Rationalism) के रूप में जाना जाता है,ज्ञान प्राप्त करने के साधन के रूप में कारण के उपयोग के आधार पर दुनिया को समझने की एक विधि थी।
उपर्युक्त प्रश्नों के उत्तर द्वारा गणितज्ञ रेने देकार्त (Mathematician Rene Descartes),रेने देकार्त (Rene Descartes) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Mathematician Rene Descartes
गणितज्ञ रेने देकार्त (Mathematician Rene Descartes)
Mathematician Rene Descartes
गणितज्ञ रेने देकार्त (Mathematician Rene Descartes) का जन्म 31 मार्च सन् 1596 ईस्वी को फ्रांस के तुरेन नामक स्थान
में सन् 1596 ईस्वी में हुआ।उनके पिता धनाढ्य थे।रेने देकार्त बहुत कमजोर बालक थे।
उनके पिता चाहते थे कि उनका पुत्र आराम का जीवन व्यतीत करें।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |