Mathematician Archimedes
Contents
hide
1.गणितज्ञ आर्किमिडीज (Mathematician Archimedes),आर्किमिडीज (Archimedes):
- गणितज्ञ आर्किमिडीज (Mathematician Archimedes) का जन्म साइराक्यूज (Syracuse) (सिसिली द्वीप) में 287 ईस्वी पूर्व में हुआ था।उनकी शिक्षा सिकंदरिया के विश्वविद्यालय में हुई थी।बहुत संभव है की आर्किमिडीज के जन्म के समय यूक्लिड अभी जीवित थे।आर्किमिडीज ने यूक्लिड के किसी शिष्य से ज्यामिति पढ़ी होगी।
- आर्किमिडीज के भुल्लकड़ स्वभाव के बारे में सभी ने एक-दो किस्से अवश्य सुने होंगे।वह किस्सा तो अवश्य सुना होगा जिसमें वे नंगे ही सड़क पर दौड़ पड़ते हैं,यह चिल्लाते हुए कि: ‘यूरेका,’यूरेका’ अर्थात् मैंने पा लिया,मैंने पा लिया!
आर्किमिडीज एक ग्रीक वैज्ञानिक थे।उन्होंने एक सिद्धांत की खोज की जो उन्हीं के नाम से विख्यात है।यह सिद्धांत उन्होंने यह देखने के बाद खोजा कि नहाने के टब में घुसने पर पानी बाहर बहने लगता है।वे सड़कों पर यूरेका (Eureka),यूरेका चिल्लाते हुए भागे जिसका अर्थ है “मैंने पा लिया है”। - इस ज्ञान का उपयोग उन्होंने राजा के मुकुट में उपयोग हुए सोने की शुद्धता को मापने के लिए किया।
उनके यांत्रिकी तथा ज्यामिति में किए गए कार्यो ने उन्हें प्रसिद्ध कर दिया।उत्तोलक,घिरनी तथा पहिया और धुरी के विषय में उनके ज्ञान ने ग्रीक सेना को रोमन सेना के विरुद्ध लड़ाई में बहुत सहायता की। - आर्किमिडीज ने विज्ञान के क्षेत्र में अनेक मौलिक आविष्कार किए।उन्होंने समतल तथा ठोस ज्यामिति में बहुत-सी नहीं बातें खोजी।उन्होंने यांत्रिकी तथा द्रव स्थिति विज्ञान के सवालों के लिए ज्यामिति का इस्तेमाल किया था।पहले के ज्यामितिकारों ने वृत्त को वर्ग में बदलने की कोशिश की थी।आर्कमिडीज ने परवलय (पैराबोला) को वर्गाकार देने का प्रयत्न किया।यूदोक्सु तथा यूक्लिड ने गोल तथा सिलेंडर पर जो बातें लिखी थी,आर्किमिडीज ने उन बातों को आगे बढ़ाया।यूक्लिड के ‘मूलतत्त्व’ की ज्यामिति को आगे बढ़ाकर आर्किमिडीज ने वक्र रेखाओं से आबद्ध समतल आकृतियों के क्षेत्रफलों को ज्ञात करने की विधि खोज निकाली।इसी विधि का विकास न्यूटन तथा लाइबनिट्ज ने किया और कलन शास्त्र को जन्म दिया।
- सिलेंडर तथा गोल के आयतन की खोज को आर्किमिडीज बड़ा महत्त्व देते थे।इसीलिए उन्होंने इच्छा जाहिर की थी कि मृत्यु के बाद उनकी समाधि पर सिलेंडर से घिरे हुए गोल की आकृति बना दी जाए!उनकी मृत्यु 212 ईस्वी पूर्व में हुई थी।
- आर्किमिडीज की इस अंतिम इच्छा से अंदाजा लगा सकते हैं कि वे ज्यामिति से कितना प्यार करते थे। यह भी अंदाजा लगा सकते हैं कि यूक्लिड तथा उनके ग्रंथ के लिए आर्किमिडीज के मन में कितना अधिक आदर भाव रहा होगा।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Crown of Greek Mathematics Eudoxus
(1.)आर्कमिडीज का सिद्धांत (Principle of Archimedes):
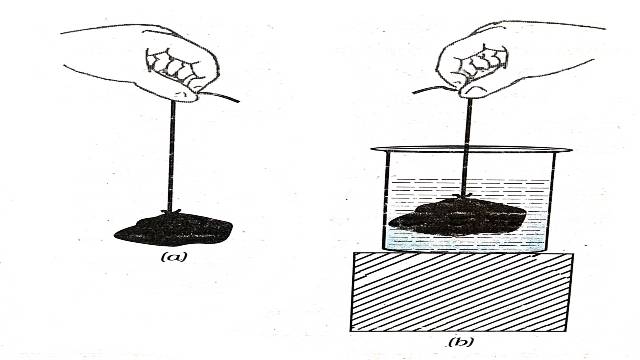
- किसी द्रव में पूर्ण अथवा आंशिक रूप से डूबी हुई वस्तु के भार में कमी उसके द्वारा हटाए हुए द्रव की मात्रा के समान होती है।
- प्रयोग:एक पत्थर का टुकड़ा लीजिए और इसे कमानीदार तुला या रबड़ की डोरी के एक सिरे से बांधिए।तुला या डोरी को पकड़कर पत्थर को लटकाएं।पत्थर के भार के कारण रबड़ की डोरी की लंबाई में वृद्धि या कमानीदार तुला का पाठ्यांक नोट कीजिए।
- अब पत्थर को एक बर्तन में रखे पानी में धीरे से डुबोइए।आप देखेंगे कि जैसे ही पत्थर को धीरे-धीरे पानी में नीचे ले जाते हैं,डोरी की लंबाई में या तुला के पाठ्यांक में कमी आती है।तथापि जब पत्थर पानी में पूरी तरह डूब जाता है तो उसके बाद कोई परिवर्तन नहीं दिखाई देता।डोरी के प्रसार या तुला की माप में कमी उत्प्लावन बल के कारण होता है।
- हम जानते हैं कि रबड़ की डोरी की लंबाई में परिवर्तन या तुला के पाठ्यांक में वृद्धि,पत्थर के भार के कारण होती है।क्योंकि पत्थर को पानी में डुबाने पर इन वृद्धियों में कमी आ जाती है।इसका अर्थ है कि पत्थर पर ऊपर की दिशा में कोई बल लगता है।इसके परिणामस्वरूप रबड़ की डोरी पर लगने वाला नेट बल कम हो जाता है और इसीलिए लंबाई की वृद्धि में भी कमी आ जाती है।जैसाकि ऊपर उल्लेख किया जा चुका है कि पानी द्वारा ऊपर की ओर लगाया गया यह बल उत्प्लावन बल कहलाता है।
- यह उत्प्लावन बल भिन्न-भिन्न द्रवों में एक ही वस्तु के लिए अलग-अलग होता है।
जैसे गिलास के पानी में बर्फ है तो बर्फ के पिघलने पर पानी गिलास के बाहर नहीं आएगा क्योंकि बर्फ के पिघलने पर प्राप्त जल का आयतन उसके द्वारा हटाए गए जल के आयतन के समान ही होगा।अगर गिलास में जल के स्थान पर अन्य द्रव लिया जाए जिसका घनत्व पानी के घनत्व से अधिक है तो बर्फ के पिघलने पर प्राप्त जल का आयतन उसके द्वारा हटाए गए द्रव के आयतन से अधिक होगा अतः गिलास से द्रव बाहर आएगा।अगर द्रव का घनत्व पानी से कम हो तो इसका विपरीत परिणाम देखने को मिलेगा। - आर्किमिडीज के सिद्धांत के बहुत से अनुप्रयोग हैं। यह जलयानों तथा पनडुब्बियों के डिजाइन बनाने में काम आता है।दूग्धमापी,जो दूध के किसी नमूने की शुद्धता की जांच करने के लिए प्रयुक्त होते हैं तथा हाइड्रोमीटर जो द्रवों का घनत्व मापने के लिए प्रयुक्त होते हैं,इसी सिद्धांत पर आधारित है।
(2.)गणितज्ञ आर्किमिडीज का गणित में योगदान (Contribution of Mathematician Archimedes):
- आर्किमिडीज एक यूनानी गणितज्ञ,भौतिक विज्ञानी, इंजीनियर और खगोल शास्त्री थे।हालांकि उनके बारे में बहुत कम लिखित जानकारी मिलती है।उन्हें सभी सदियों के सर्वश्रेष्ठ तीन महान् गणितज्ञों आइज़क न्यूटन,कार्ल फ्रैडरिक गाउस में गिनती की जाती है।आर्किमिडीज ने आधुनिक कैलकुलस और विश्लेषण लगाने के लिए असीम रूप से छोटे और थकावट विधि को लागू किया और ज्यामिति प्रमेय की एक श्रृंखला को सिद्ध किया (Modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems.)।इसके साथ ही उन्होंने एक वृत्त का क्षेत्रफल,गोले का पृष्ठीय क्षेत्रफल और आयतन,दीर्घवृत्त का क्षेत्रफल (area of ellipse),एक परवलय के तहत क्षेत्रफल (The area under a parabola),परिक्रमण के परवलयज के एक खंड का आयतन (The volume of a segment of a paraboloid of revolution),परिक्रमण के अतिपरवलय के एक खंड का आयतन (The volume of a segment of a hyperboloid of revolution) और एक सर्पिल का क्षेत्रफल (area of a spiral) ज्ञात किया।
- उनकी अन्य गणितीय उपलब्धियों में पाई का एक सन्निकटन मान 3\frac{1}{7} (लगभग 3.1429) और 3\frac{10}{71} (लगभग 3.1408) के बीच ज्ञात करना था जो पाई के मान 3.1416 के सन्निकट था।
- वह भौतिक घटनाओं के लिए गणित को लागू करने वाले पहले लोगों में से एक थे जिन्होंने हाइड्रोस्टैटिक्स (Hydrostatics) और स्टैटिक्स (Statics) की स्थापना की।इस क्षेत्र में आर्किमिडीज की उपलब्धियों में लीवर के सिद्धांत का प्रमाण (proof of the principle of the lever),गुरुत्वाकर्षण के केंद्र की अवधारणा का व्यापक उपयोग (The widespread use of the concept of center of gravity) और उत्प्लावन बल के नियम का प्रतिपादन शामिल है (Enunciation of the law of buoyancy)। उन्हें अपने सिरेक्यूज को रोमन सेना के आक्रमण से बचाने के लिए नवीन मशीनों जैसे कि उनके स्क्रु पंप (Srew pump),कंपाउंड कुली (Compound pulleys) और रक्षात्मक युद्ध मशीनों को डिजाइन करने का श्रेय दिया जाता है।जिससे रोमन सिपाही आर्किमिडीज से बहुत डरने लगे।वे आर्किमिडीज को ज्यामिति का महादानव कहने लगे।इससे प्रभावित होकर रोमन सेनापति मार्कस क्लाॅडियस मार्सेलस (Marcus Claudius Marcellus) आर्किमिडीज का सम्मान करना चाहता था।
- आर्किमिडीज ने 12-गाॅन (12 भुजाओं की आकृति) की भुजा की गणना की जो कि सम बहुभुज की भुजाओं की पुनरावृति है।आर्किमिडीज एक तरह अविभाज्य (इनफिनिटिमल्स के लिए एक अग्रदूत (a precursor to infinitesibles) का उपयोग करने में सक्षम था जो आधुनिक समाकलन (Modern Integral Calculus) के समान है। विरोधाभास पद्धति के माध्यम से वह सटीकता की एक स्वेच्छ डिग्री के लिए समस्याओं का उत्तर दे सकता था जबकि उसकी उस सीमा को निर्दिष्ट करता था जिसके भीतर उत्तर निहित था।इस तकनीक को थकावट की विधि (Method of Exhaustion) के रूप में जाना जाता है और उन्होंने इसे आकृतियों के क्षेत्रफलों (Area of Figures) और π के मान का अनुमान लगाने के लिए नियोजित किया।
- एक वृत्त के मापन में उसने एक वृत के बाहर एक बड़ा सम षट्भुज और फिर वृत के अंदर एक छोटा सम षट्भुज और प्रत्येक सम बहुभुज के भुजाओं की संख्या को उत्तरोत्तर दोगुना करते हुए,प्रत्येक बहुभुज के एक भुजा की लंबाई की गणना करके ऐसा किया।जैसे-जैसे भुजाओं की संख्या बढ़ती है, यह एक वृत्त का अधिक सटीक सन्निकटन बन जाता है।ऐसे चार चरणों के बाद,जब बहुभुजों में प्रत्येक में 96 भुजाएं थी,वह यह निर्धारित करने में सक्षम था कि π का मान 3\frac{1}{7} (लगभग 3.1429) और 3\frac{10}{71} (लगभग 3.1408) के बीच है जो इसके वास्तविक मान 3.1416 के अनुरूप है।उन्होंने यह भी साबित किया कि एक वृत्त का क्षेत्रफल π को वृत्त की त्रिज्या के वर्ग से गुणा करने के बराबर होता है।
- गोला और सिलेंडर पर आर्किमिडीज यह बताते हैं कि किसी भी परिणाम को पर्याप्त गुना में जोड़ने पर दिए गए परिणाम से अधिक होगा।आज यह वास्तविक संख्या के आर्किमिडियन गुणधर्म (Archimedean Property of real numbers) के रूप में जाना जाता है।
- आर्किमिडीज एक सर्कल (Curcle) के मापन \frac{265}{153} लगभग (लगभग 1.732026) और \frac{1351}{780} (लगभग 1.7320508) के बीच स्थित 3 के वर्गमूल का मान देता है।वास्तविक मान 1.7320508 है जो इसे बहुत सटीक अनुमान बनाता है।
- अनन्त श्रृंखला (Infinite Series):
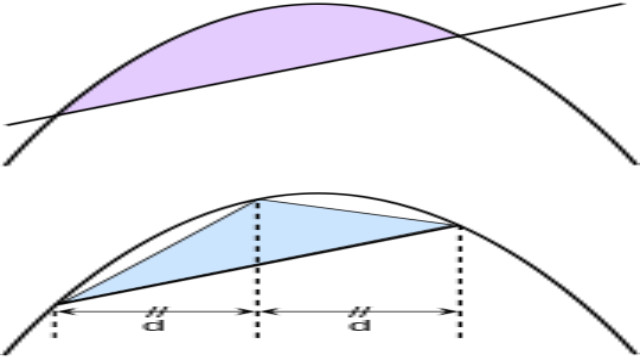
- एक प्रमाण है कि ऊपरी आकृति में परवलयिक खंड का क्षेत्रफल परवलय के क्षेत्रकलन से निचली आकृति में अंकित त्रिभुज के \frac{4}{3} बराबर है।परवलय के क्षेत्रकलन (Quadrature of parabola) में आर्किमिडीज ने साबित किया कि परवलय और एक सीधी रेखा से घिरा एक संबंधित खुदा हुआ त्रिभुज के क्षेत्रफल का \frac{4}{3} गुना है जैसा कि दाईं ओर की आकृति में दिखाया गया है।उन्होंने समस्या के समाधान को अनंत ज्यामितीय श्रृंखला के रूप में सामान्य अनुपात \frac{1}{4} के साथ व्यक्त किया:
\Sigma_{n=0}^{\infin{}} 4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+4^{-4}+\cdot\cdot\cdot=\frac{4}{3}
- यदि इस श्रृंखला का पहला पद त्रिभुज का क्षेत्रफल है तो दूसरा दो त्रिभुजों के क्षेत्रफल का योग है जिनके आधार दो छोटी छेदक रेखाएँ हैं और जिनका तीसरा शीर्ष वह स्थान है जहां पर परवलय की धुरी के समानांतर रेखा है और जो आधार के मध्य बिंदु से होकर गुजरता है,परवलय को काटता है।इस प्रूफ में \frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\frac{1}{256}+... श्रृंखला की विविधता का उपयोग किया गया है जिसका योग \frac{1}{3} है।
(3.)गणतज्ञ आर्किमिडीज का सम्मान (गणितज्ञ आर्किमिडीज (Honour of Mathematician Archimedes):
- गणित का नोबेल पुरस्कार माना जाने वाला फील्ड्स मेडल में आर्किमिडीज का एक चित्र होता है।विज्ञान और गणित के इतिहासकार लगभग सार्वभौमिक रूप से इस बात से सहमत है कि आर्किमिडीज पुरातन काल से बेहतरीन गणितज्ञ थे।एरिक टेंपल बेल ने लिखा है:सभी इतिहास के 3 महानतम गणितज्ञों की किसी भी सूची में आर्किमिडीज का नाम शामिल होगा।इसी तरह अल्फ्रेड नॉर्थ व्हाइटहेड और जाॅर्ज एफ सीमन्स ने आर्किमिडीज के बारे में कहा है:यदि हम विचार करें कि अन्य सभी लोगों ने गणित और भौतिकी में हर महाद्वीप पर और हर सभ्यता में समय की शुरुआत से लेकर 17 वीं शताब्दी तक पश्चिमी यूरोप में क्या हासिल किया है तो आर्किमिडीज की उपलब्धियां इस सबसे अधिक महत्वपूर्ण है।वह अपने आप में एक महान सभ्यता थे।रेवील नेट्ज,स्टैनफोर्ड विश्वविद्यालय में ग्रीक गणित और खगोल विज्ञान में प्रोफेसर आर्किमिडीज के लिए कहते हैं:चूँकि आर्किमिडीज ने कैलकुलस के निर्माण के लिए किसी ओर की तुलना में अधिक नेतृत्व किया और चूँकि वह भौतिक दुनिया में गणित के अनुप्रयोग के अग्रणी थे इसलिए यह पता चला कि पश्चिम विज्ञान आर्किमिडीज के लिए फुटनोट की एक श्रृंखला है। इस प्रकार यह पता चला कि आर्किमिडीज अब तक जीवित रहने वाले सबसे महत्वपूर्ण वैज्ञानिक हैं।
- उपर्युक्त आर्टिकल में गणितज्ञ आर्किमिडीज (Mathematician Archimedes),आर्किमिडीज (Archimedes) के बारे में बताया गया है।
(4.)गणितज्ञ आर्किमिडीज का परिवार (Family of Mathematician Archimedes):
- गणितज्ञ आर्किमिडीज (Mathematician Archimedes) के परिवार के बारे में कोई जानकारी उपलब्ध नहीं है।उन्होंने शादी की थी या नहीं की थी।यदि की थी तो उनके कितने पुत्र तथा पुत्रियाँ थी,इसके बारे में कोई जानकारी उपलब्ध नहीं है।उनके पिता फ़िडियास (Phidias) बताया जाता है।
Also Read This Article:Mathematician Euclid
(5.)गणितज्ञ आर्किमिडीज का निष्कर्ष (Conclusion of Mathematician Archimedes):
- गणितज्ञ आर्किमिडीज (Mathematician Archimedes) सच्चे अर्थों में कर्मयोगी थे।गीता के अनुसार कर्म दो प्रकार से किया जाता है सकाम कर्म एवं निष्काम कर्म।सकाम कर्म बंधनों में डालने वाला है परंतु निष्काम कर्म बंधनों से मुक्त करने वाला है।इसलिए निष्काम कर्म करने वाला ही सच्चे अर्थों में कर्मयोगी होता है।क्योंकि कर्म किए बिना कोई भी व्यक्ति किसी भी क्षण भी नहीं रह सकता है।निष्काम कर्म अर्थात् जिसकी फल प्राप्ति में कोई आसक्ति नहीं है।गणितज्ञ आर्किमिडीज (Mathematician Archimedes) अंतिम समय भी अपने कर्म गणित की गवेषणा कार्य में ही लीन थे।उन्होंने विजयी रोमी सेना के सैनिक तथा सेनापति मार्सेलिस की आज्ञा तथा बंधन को स्वीकार नहीं किया।
गणितज्ञ आर्किमिडीज (Mathematician Archimedes) आजीवन अपनी मौज में ही जिए और अपनी मौज में ही मरे।वास्तव में आज हम गणित का जो स्वरूप देख रहे हैं तथा दैनिक जीवन में गणित का लाभ उठा रहे हैं इसके पीछे गणितज्ञ आर्किमिडीज (Mathematician Archimedes),गणितज्ञा हाइपेटिया जैसे कर्मयोगियों का त्याग,तप,समर्पण ही है।उन्होंने गणित का संपूर्ण कार्य पूरी मानव जाति के कल्याण हेतु ही किया है।अपने प्राणों की परवाह न करते हुए भी सेनापति मार्सेलिस का हुकुम नहीं माना।जीवनभर उन्होंने अहंकार रहित होकर कर्म किया। गणित से वे कितना प्रेम करते थे,यह इस कथन से ही प्रगट हो जाता है कि उन्होंने अपनी अंतिम इच्छा जाहिर की थी कि उनकी समाधि पर सिलेंडर से बनी गोल की आकृति बना दी जाए। - उपर्युक्त विवरण में गणितज्ञ आर्किमिडीज (Mathematician Archimedes),आर्किमिडीज (Archimedes) की समीक्षा की गई है।
2.गणितज्ञ आर्किमिडीज (Mathematician Archimedes),आर्किमिडीज (Archimedes) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.आर्किमिडीज ने गणित में क्या खोजा? (What did Archimedes discover in mathematics?):
उत्तर:गणितज्ञ आर्किमिडीज को प्राचीन इतिहास का सबसे महान गणितज्ञ माना जाता है और सभी समय के महानतम में से एक।आर्किमिडीज ने आधुनिक कलन और विश्लेषण का अनुमान लगाया है,जिसमें असीम रूप से छोटे की अवधारणा और थकावट की विधि (method of exhaustion) को प्राप्त करने और कड़ाई से साबित करने के लिए ज्यामितीय प्रमेयों की एक श्रृंखला शामिल है।
प्रश्न:2.आर्किमिडीज किसलिए प्रसिद्ध है? (What is Archimedes famous for?):
उत्तर:गणितज्ञ आर्किमिडीज (Mathematician Archimedes)आर्किमिडीज (जन्म 287 ईसा पूर्व, सिरैक्यूज़,सिसिली [इटली] (Syracuse, Sicily [Italy]) तथा मृत्यु 212/211 ईसा पूर्व, सिरैक्यूज़),प्राचीन ग्रीस में सबसे प्रसिद्ध गणितज्ञ और आविष्कारक थे।आर्किमिडीज विशेष रूप से एक गोले की सतह और आयतन और उसके परिबद्ध बेलन (surface and volume of a sphere and its circumscribing cylinder) के बीच संबंध की खोज के लिए महत्वपूर्ण है।
प्रश्न:3.आर्किमिडीज को गणित का जनक क्यों कहा जाता है? (Why Archimedes is known as father of mathematics?):
उत्तर:आर्किमिडीज को गणित और विज्ञान में उनके उल्लेखनीय आविष्कारों के कारण गणित का जनक माना जाता है।वह सिरैक्यूज़ के राजा हिरो द्वितीय की सेवा में था (King Hiero II of Syracuse)। उस समय उन्होंने कई आविष्कार किए।
सबसे उत्कृष्ट उपलब्धि के इस चरण का उपयोग गणित में एक वृत्त की माप की गणना के लिए किया जाता है।
प्रश्न:4.आर्किमिडीज ने किसका आविष्कार और खोज की थी? (What did Archimedes invent and discover?):
उत्तर:गणितज्ञ आर्किमिडीज (Mathematician Archimedes) तीसरी शताब्दी ईसा पूर्व में, आर्किमिडीज ने यांत्रिकी (mechanics) और हाइड्रोस्टैटिक्स (hydrostatics) के विज्ञान का आविष्कार किया।लीवर (levers) और पुली (pulleys) के नियमों की खोज की जो हमें छोटे बलों का उपयोग करके भारी वस्तुओं को स्थानांतरित करने की अनुमति देते हैं।भौतिकी की सबसे मौलिक अवधारणाओं में से एक का आविष्कार किया – गुरुत्वाकर्षण का केंद्र (center of gravity)।
प्रश्न:5.क्या आर्किमिडीज ने पाई का आविष्कार किया था? (Did Archimedes invent pi?):
उत्तर:π की पहली गणना सिरैक्यूज़ के आर्किमिडीज़ (287-212 ईसा पूर्व) द्वारा की गई थी,जो प्राचीन दुनिया के महानतम गणितज्ञों में से एक थे।आर्किमिडीज जानता था कि उसने π का मान नहीं पाया था बल्कि उन सीमाओं के भीतर केवल एक सन्निकटन पाया था।इस प्रकार, आर्किमिडीज ने दिखाया कि π का मान 3 1/7 और 3 10/71 के बीच है।
प्रश्न:6.आर्किमिडीज के सिद्धांत की खोज कैसे हुई? (How was the Archimedes principle discovered?):
उत्तर:आर्किमिडीज ने मुकुट के वजन के बराबर सोना और चांदी का एक द्रव्यमान लिया।उस आर्किमिडीज ने अपने सिद्धांत की खोज की जब उसने अपने बाथटब में पानी को ऊपर उठते देखा और वह “यूरेका (Eureka)!” चिल्लाते हुए नग्न होकर बाहर निकला।”मैंने इसे पाया है!” को कहानी का बाद का अलंकरण माना जाता है
प्रश्न:7.आर्किमिडीज का सबसे बड़ा आविष्कार क्या था? (What was Archimedes greatest invention?):
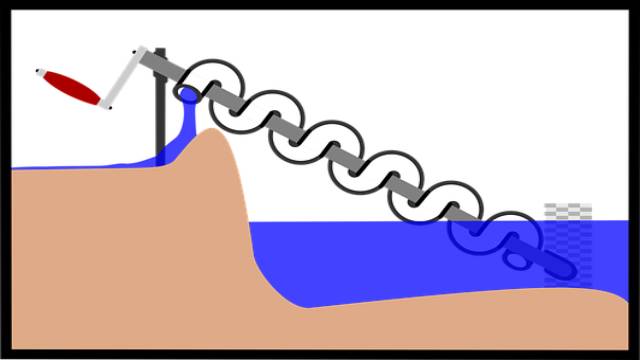
उत्तर:आर्किमिडीज अपने आविष्कारों और वैज्ञानिक खोजों के लिए प्रसिद्ध थे।इनमें से सबसे प्रसिद्ध थे आर्किमिडीज का पेंच (पानी जुटाने के लिए एक उपकरण जो आज भी फसल सिंचाई और सीवेज उपचार संयंत्रों में उपयोग किया जाता है) और आर्किमिडीज का उतप्लावन का सिद्धांत (Archimedes’ principle of buoyancy)
उपर्युक्त प्रश्नों के उत्तर द्वारा गणितज्ञ आर्किमिडीज (Mathematician Archimedes),आर्किमिडीज (Archimedes):
Mathematician Archimedes
गणितज्ञ आर्किमिडीज (Mathematician Archimedes)
Mathematician Archimedes
गणितज्ञ आर्किमिडीज (Mathematician Archimedes) का जन्म साइराक्यूज (Syracuse) (सिसिली द्वीप) में 287 ईस्वी पूर्व में हुआ था।
उनकी शिक्षा सिकंदरिया के विश्वविद्यालय में हुई थी।बहुत संभव है की आर्किमिडीज के जन्म के समय यूक्लिड अभी जीवित थे।
आर्किमिडीज ने यूक्लिड के किसी शिष्य से ज्यामिति पढ़ी होगी।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
