mathematical GIFs that will make mathematics finally make sense
Contents
hide
1
आवश्यक गणितीय जीआईएफ जो गणित को आखिरकार बना देगा (mathematical GIFs that will make mathematics finally make sense):
आवश्यक गणितीय जीआईएफ जो गणित को आखिरकार बना देगा (mathematical GIFs that will make mathematics finally make sense):
- आवश्यक गणितीय जीआईएफ जो गणित को आखिरकार बना देगा (mathematical GIFs that will make mathematics finally make sense) में बताया गया है कि जीआईएफ गणित को अर्थयुक्त बना देता है.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Who gets to be called a mathematician
1.आवश्यक गणितीय जीआईएफ जो गणित को आखिरकार बना देगा (mathematical GIFs that will make mathematics finally make sense):
- हां, गणित की पाठ्यपुस्तकें पाठ के उबाऊ, स्थिर खंडों, संख्याओं और सूत्रों से भरी होती हैं। और कोई नहीं, विशेष रूप से छात्र लंबे ट्यूटोरियल की तरह नहीं हैं। तो, छात्र, हमारा भविष्य, सबसे कठिन विषय, गणित, स्कूल में कैसे सीखेंगे?
- इन स्थितियों में, मुझे लगता है कि गणित को पढ़ाने का एक वैकल्पिक तरीका है। यह “GIFs है।” हाँ, उन अजीब छोटी वीडियो क्लिप जो आप हमेशा ट्विटर पर देख रहे हैं। आप यह पूछ सकते हैं;
- “उन नासमझ चलती छवियों को शिक्षा के लिए कैसे इस्तेमाल किया जा सकता है?”
और मैं कह सकता हूं कि सौभाग्य से, वास्तव में हमारे कक्षाओं में GIF का उपयोग करने के कई तरीके हैं। हालांकि जीआईएफ एनिमेशन का उपयोग तकनीकी उपकरण के रूप में किया जाता है जो गणित शिक्षा में बहुत दुर्लभ है, आप इन एनिमेशनों के साथ उन चीजों को कर सकते हैं जो आप सादे पाठ के साथ नहीं कर सकते। उदाहरण के लिए, छात्रों को बार-बार निर्देश बताने के बजाय, बस प्रत्येक चरण के लिए एक GIF बनाएं। और फिर छात्र इसे महत्वपूर्ण और समाधान या सूत्र के सभी भागों को देखेंगे और याद रखेंगे। आप अपने छात्रों को सीखते और हँसाते रहेंगे। यह आपके विद्यालय में सबसे अच्छे शिक्षक होने का एक अच्छा तरीका हो सकता है।
Also Read This Article:GIF
- यदि आप अभी तक अच्छे हैं, तो आइए कुछ खूबसूरत गणितीय GIF पर नज़र डालें और जानें!
2.14 / pi क्या है और यह 3.14something क्यों है?(What is π/pi and why is it 3.14something?):
- 14 / pi क्या है और यह 3.14something क्यों है?
आइए एक वृत्त को मापने का प्रयास करें। व्यास और त्रिज्या सीधी रेखाएँ हैं। हम उन्हें एक शासक के साथ आसानी से माप सकते हैं। लेकिन परिधि पाने के लिए, यह इतना आसान नहीं है। एक वृत्त और व्यास की परिधि के बीच संबंध इतना अनूठा है। जब हम व्यास द्वारा परिधि को विभाजित करते हैं, तो हमें हमेशा एक ही नंबर मिलेगा, चाहे सर्कल कितना भी बड़ा या छोटा हो। लेकिन दिलचस्प बात यह है कि हम इसे दो पूरे संख्याओं के अनुपात के रूप में व्यक्त नहीं कर सकते। हम केवल पास हो सकते हैं। यह अंकों की एक श्रृंखला है, जो 3.14159 से शुरू होती है और हमेशा के लिए जारी रहती है! इसीलिए, हर बार अनंत अंकों को लिखने की कोशिश करने के बजाय, हम ग्रीक अक्षर i / pi का उपयोग करना पसंद करते हैं। - यहां तक कि छात्रों को केवल s के पहले 2 अंकों की आवश्यकता होती है, दसियों वैज्ञानिक और गणितज्ञ mystery के रहस्य का पता लगाने की कोशिश कर रहे हैं। उनके पास सुपर पावर क्वांटम कंप्यूटर हैं और अब तक उन्होंने दो क्वाड्रिलियन अंकों तक की गणना की है। और एक आदमी है जिसने is के पहले 67,000 अंकों को याद किया है।
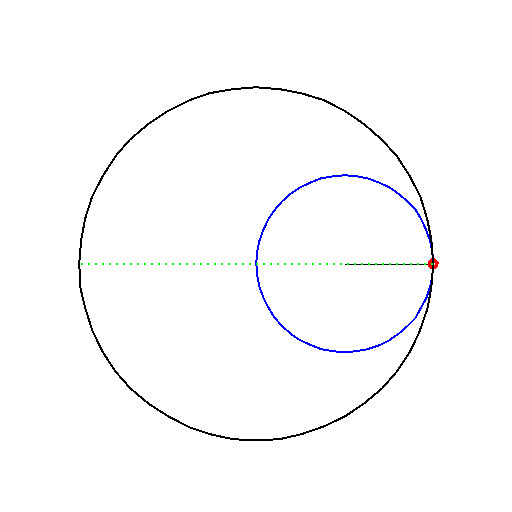
- Tusi Couple
प्रश्न: क्या होता है जब हम एक सर्कल को एक सर्कल के अंदर रोल करते हैं जो वास्तव में दो बार बड़ा होता है? - उत्तर: मुझे पता है, सिर में चित्र बनाना बहुत कठिन है। यही कारण है कि GIF का उपयोग करना आपके लिए एक सही तरीका है।
3.पूरे सर्कल को कवर करने के लिए हमें कितने आर्क्स चाहिए? (How many arcs do we need to cover the entire circle?):
- चाप की लंबाई r है और परिधि 2 .r है। इसका मतलब है कि परिधि को कवर करने के लिए हमें 2π आर्क्स की आवश्यकता होगी।
4.एक ही खंड में कोण समान क्यों हैं?(Why are the angels in the same segment equal?):
- इस प्रमाण के लिए, आप इतने सारे पाठ और ज्यामितीय शब्दों का उपयोग कर सकते हैं, लेकिन अधिकांश छात्र समझ नहीं पाएंगे।
- यदि वे कॉलेज के छात्र नहीं हैं, तो एक GIF पूरी तरह से काम करेगा।
Also Read This Article:Guesswork often leads different minds to same conclusion
5.एक वृत्त का क्षेत्रफल क्या है? (What is the area of a circle?):
- शुरुआत में, हाई स्कूल के छात्रों के लिए, क्षेत्र का मतलब सामान्य रूप से “ऊंचाई का आधार” होता है। लेकिन जब वे देखते हैं कि वे उस सर्कल के हैं जो “² टाइम्स आर” है, तो वे क्यों पूछ सकते हैं?
- एक दीर्घवृत्त कैसे आकर्षित करें? एक एनीमेशन जो दीर्घवृत्त की व्याख्या करता है। छोटे वर्गों द्वारा चिह्नित दो बिंदुओं को दीर्घवृत्त का “फॉसी” कहा जाता है।
- 2 दीर्घवृत्त होते हैं, जिनकी ऊँचाई उनकी चौड़ाई से आधी होती है, एक वृत्त में जुड़ जाते हैं।
6.पहली प्रमुख संख्या और फाइबोनैचि श्रृंखला क्या हैं? (What are the first prime numbers and Fibonacci series?):
- एक अभाज्य संख्या 1 से अधिक एक पूर्ण संख्या है, जिसके केवल कारक 1 और स्वयं हैं एक कारक एक संपूर्ण संख्या है जिसे समान रूप से दूसरी संख्या में विभाजित किया जा सकता है।
- फाइबोनैचि श्रृंखला संख्याओं की एक श्रृंखला है जिसमें प्रत्येक संख्या दो पूर्ववर्ती संख्याओं का योग है। सबसे सरल श्रृंखला 1, 1, 2, 3, 5, 8, आदि है।
Eratosthenes एनीमेशन की चलनी
गणित केवल एक्स के लिए हल नहीं कर रहा है, यह भी पता लगा रहा है कि क्यों। - फाइबोनैचि संख्याओं के कई और अनुप्रयोग हैं। यदि आप उन्हें करीब से देखते हैं, तो आपको उनके अंदर दबी हुई फाइबोनैचि संख्या दिखाई देगी। उदाहरण के लिए, यदि आप बड़ी संख्या को छोटी संख्या से विभाजित करते हैं, तो ये अनुपात करीब 1.618 के करीब और करीब हो जाते हैं, जिसे कई लोग गोल्डन रेशियो के रूप में जानते हैं, एक ऐसी संख्या जिसने सदियों से गणितज्ञों, वैज्ञानिकों और कलाकारों को मोहित किया है।
7.हम कैसे जानते हैं कि a² + b² = c P (पायथागॉरियन प्रमेय)[How do we know that a² + b² = c² (Pythagorean Theorem)]:
- पाइथागोरस प्रमेय, नियम जो एक सही त्रिकोण के लिए कहता है, एक तरफ का वर्ग प्लस दूसरी तरफ का वर्ग कर्ण के वर्ग के बराबर है।
- दूसरे शब्दों में, a² + b² = c words। यह कथन ज्यामिति के सबसे मौलिक नियमों में से एक है।
लेकिन हम कैसे जानते हैं कि प्रमेय हर सही त्रिकोण के लिए सही है?
क्योंकि हम इसे साबित कर सकते हैं। - सबूत मौजूदा गणितीय नियमों और तर्क का उपयोग करते हैं कि यह प्रदर्शित करने के लिए कि एक प्रमेय को हर समय सही होना चाहिए।
- यदि आप वास्तव में खुद को विश्वास दिलाना चाहते हैं, तो आप एक समकोण त्रिभुज के चारों ओर एक-दूसरे से जुड़े समान गहराई के तीन वर्ग बक्से के साथ एक टर्नटेबल का निर्माण कर सकते हैं। यदि आप पानी के साथ सबसे बड़ा वर्ग भरते हैं और टर्नटेबल को स्पिन करते हैं, तो बड़े वर्ग का पानी दो छोटे लोगों को पूरी तरह से भर देगा।
पाइथागोरस प्रमेय। - हम एक गोले पर तीन 90 डिग्री के कोण के साथ एक त्रिकोण कैसे खींच सकते हैं?
बहुभुज का बाहरी कोण 360 के बराबर क्यों होता है?
हम हलकों का उपयोग करके एक वर्ग का निर्माण कैसे कर सकते हैं?
8.हेबरडैशर समस्या (The Haberdasher Problem):
- इस पहेली के लिए, तीन कटौती के साथ, हमें एक समभुज त्रिकोण को एक वर्ग में विभाजित करना होगा।
एफओआईएल विधि और प्रथम के योग क्या हैं
9.पहली n प्राकृतिक संख्या के FOIL विधि और योग क्या हैं? (What are the FOIL method and Sum of the First n Natural Numbers?):
- प्राथमिक बीजगणित में, एफओआईएल दो द्विपद को गुणा करने का एक मानक तरीका है।
- प्रत्येक द्विपद के पहले (“पहले” शब्दों को एक साथ गुणा किया जाता है)
बाहरी (“बाहर” शब्द कई गुना हैं – अर्थात, पहले द्विपद का पहला शब्द और दूसरे का दूसरा शब्द)
भीतर (“अंदर” शब्द कई गुना हैं – पहले द्विपद का दूसरा शब्द और दूसरे का पहला शब्द)
अंतिम (प्रत्येक द्विपद की “अंतिम” शर्तें गुणा की जाती हैं) - “एफओआईएल” विधि आसानी से द्विपद को गुणा करने के लिए
- आई लव यू टू, मैथ!
I LOVE YOU TOO, MATH! - उपर्युक्त आर्टिकल में आवश्यक गणितीय जीआईएफ जो गणित को आखिरकार बना देगा (mathematical GIFs that will make mathematics finally make sense) के बारे में बताया गया है.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |