Geometric Proof of Difference of Squares
1.ज्यामितीय निरूपण का परिचय (Introduction to Geometric Representation),वर्गों के अंतर का ज्यामितीय प्रमाण (Geometric Proof of Difference of Squares):
- वर्गों के अंतर का ज्यामितीय प्रमाण (Geometric Proof of Difference of Squares) अर्थात ज्यामितीय रचनाओं का अध्ययन कुछ स्वयं सिद्ध कथनों तथा अवधारणाओं के आधार पर किया जाता है जहाँ व्यक्ति का खोज करने का गुण सदैव महत्त्वपूर्ण रहता है तथा गणनाएं सदैव सहायक की भूमिका में उपस्थित रहती हैं। इस विधि को संश्लेषिक विधि (Synthetic Approach) कहते हैं ।ऐसी स्थिति में कभी-कभी समस्याओं को हल करना कठिन हो जाता है अतः सभी ज्यामितीय समस्याओं को एक समान रूप से हल करने के लिए यह आवश्यक है कि व्यक्ति के खोज करने वाले गुण के प्रभाव को नगण्य बना दिया जाए तथा गणनाओं को मुख्य आधार प्रदान कर दिया जाए। ज्यामितीय निरूपण इस प्रकार के कार्य में अत्यन्त सहायक सिद्ध हुआ है। इस पद्धति में हम रेखाचित्र द्वारा संख्याओं को निरूपित करते हैं एवं ज्यामितीय चित्रों का अध्ययन करते हैं अतः इसे ज्यामितीय निरूपण कहते हैं।चूँकि यह पद्धति ज्यामिति के चित्रों के विश्लेषण पर आधारित होती है अतः इसे वैश्लेषिक ज्यामिति (Analytic Geometry) भी कहते हैं। ज्यामिति गणित विज्ञान की एक शाखा है जिसमें रेखाचित्रों, रेखाओं, रेखाखण्डों, तलों तथा ठोस पिण्डों के गुणों और उनके आकार, विस्तार एवं स्थिति का अध्ययन किया जाता है।
- प्राचीनकाल में इस गणित में भूमिमापन का कार्य किया जाता था। परन्तु वर्तमान समय में प्रत्येक क्षेत्र में इसका प्रयोग होता। प्लेटो ने अपने घर के दरवाजे पर पर लिख रखा था कि जो व्यक्ति ज्यामिति नहीं जानता वह यहाँ प्रवेश नहीं पा सकता है। ज्यामिति के अध्ययन के लिए अच्छे स्तर की तर्क एवं सोचने की शक्ति की आ आवश्यकता होती है। प्लेटो ने यही सोचकर शायद यह नियम अपनाया होगा। आधुनिक युग में यूक्लिड की प्रसिद्ध पुस्तक “The Elements” ज्यामितिशास्त्र का स्रोत माना जाता है। भारत में यज्ञ करने के लिए ज्यामिति का उपयोग किया जाता है। भारत के गणितज्ञों में ब्रह्मगुप्त, भास्कराचार्य, वराहमिहिर, आर्यभट्ट का इस क्षेत्र में अतुलनीय योगदान रहा है।
- यूक्लिड द्वारा ज्यामिति का संगठित विवेचन लगभग 1800 A. D. तक व्यापक रूप से स्वीकार किया जाता है यह बीजगणित के अत्यन्त धीमे विकास के कारण हुआ। लगभग 1600 A. D. के आसपास बीजगणित का स्वरूप संक्षिप्त भाषा के रूप में प्रारम्भ हुआ जिसके द्वारा कठिन एवं पेचीदा सम्बन्धों को बीजगणित की भाषा में लिखना सम्भव हुआ। इसी काल में विश्लेषिक ज्यामिति (Analytic Geometry) की खोज हुई जिससे परम्परागत ज्यामिति की समस्याओं को यांत्रिक तरीके से समस्याओं में प्रकट किया जा सका।
- यूनान के लोगों ने सर्वप्रथम निगमनात्मक चिंतन से, सुस्पष्ट तथ्यों के आधार पर, प्रमेयों को सिद्ध किया। फिर भी उन्नीसवीं शताब्दी के आरम्भ तक लोगों ने इस प्रणाली को तर्कसंगत आधार प्रदान करने में सफलता प्राप्त नहीं की।
अब आधुनिक गणित में तर्क के आधार पर संरचनाओं का निर्माण किया जाता है जिससे यह स्पष्ट है कि अभिगृहितों से विभिन्न नियमों को निष्पादित किया जा सकता है तथा इससे समझने की शक्ति का विकास होता है। - आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:the case for mathematics in writing classes
Also Read This Article:Difference of two squares
2.वर्गों के अंतर का ज्यामितीय प्रमाण(Geometric Proof of Difference of Squares): a² – b²
- दो वर्गों का अंतर एक वर्ग संख्या को दूसरे वर्ग संख्या से घटाता है। और ये संख्या पूर्ण वर्ग नहीं होगी। शुक्र है, वर्गों के अंतर को आसानी से फैक्टर किया जा सकता है।
- a² – b² गणित में सर्वव्यापी है और यह बीजगणित के लिए सुपरक्लिफ्रेगिलिस्टिसएक्सपायलीडोसियस भी है।
यदि हम बीजगणितीय रूप से बोलते हैं:
(a + b) (a – b) = a² + ba – ab -b²= a² – b² - लेकिन a² – b²का प्रतिनिधित्व करने के लिए एक अलग और सुंदर तरीका है। हम इस एकल अवधारणा के कई निरूपण कर सकते हैं। यह गणित की सुंदरता है। उदाहरण के लिए, ज्यामितीय वस्तुएं बीजीय सूत्रों और समीकरणों की कल्पना करने के लिए बहुत शक्तिशाली हैं।
- *** बीजगणित के ज्यामितीय सिद्धों के बारे में एक सुंदर किताब है जिसे कहा जाता है:द एलिमेंट्स ऑफ यूक्लिड। आप इसे प्यार करेंगे अगर आपके पास है!
आइए इसके बारे में ज्यामितीय रूप से थोड़ा विचार करें।
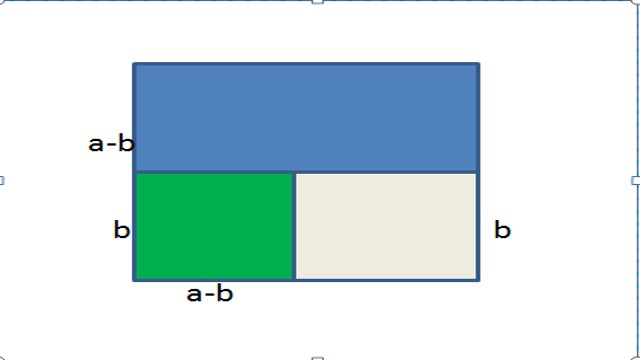
नीचे के इस नीले आकार में a² – b²का एक क्षेत्र है।और हम एक बीजीय पहचान को फिर से व्यवस्थित करके प्रकट कर सकते हैं।
- ऐसा करने के लिए, पहले हम एक कट बनाते हैं और आकृति को दो अलग-अलग आयतों में विभाजित करते हैं; नीला एक और पीला एक।नीली आयत की ऊँचाई अब (a – b) है और हरे आयत की ऊँचाई स्पष्ट रूप से b है।
- अब, यदि हम पीले आयत को पलटाते हैं और नीली आयत के बगल में रखते हैं, तो हम अपनी पुन: व्यवस्थित करते हैं। चूंकि एक आयत का क्षेत्रफल ऊंचाई की चौड़ाई है,संयुक्त आयत का क्षेत्र है;
(a + b)(a – b)।
- इस आयत में मूल आकार के समान क्षेत्र है! जिसका मतलब है;
- a² – b² = (a + b) (a – b)
कभी-कभी ज्यामितीय रूप से बीजगणित की समस्या का प्रतिनिधित्व करने के दिलचस्प परिणाम हो सकते हैं! - उपर्युक्त आर्टिकल में वर्गों के अंतर का ज्यामितीय प्रमाण (Geometric Proof of Difference of Squares) के बारे में बताया गया है.
Also Read This Article:how to make every student expert in mathematics
Geometric Proof of Difference of Squares
वर्गों के अंतर का ज्यामितीय प्रमाण
(Geometric Proof of Difference of Squares)
Geometric Proof of Difference of Squares
वर्गों के अंतर का ज्यामितीय प्रमाण (Geometric Proof of Difference of Squares) अर्थात
ज्यामितीय रचनाओं का अध्ययन कुछ स्वयं सिद्ध कथनों तथा अवधारणाओं के
आधार पर किया जाता है जहाँ व्यक्ति का खोज करने का गुण सदैव महत्त्वपूर्ण रहता है
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
