Equal Chords and Distances From Centre
1.समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Equal Chords and Distances From Centre),समान जीवाएँ और उनकी केन्द्र से दूरियाँ कक्षा 9 (Equal Chords and Distances From Their Centre Class 9):
समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Equal Chords and Distances From Centre) के बारे में अध्ययन करेंगे।समान जीवाओं की केन्द्र से दूरियों को प्रमेय व उदाहरणों द्वारा समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Circle Class 9
2.समान जीवाओं पर आधारित प्रमेय (Theorem Based on Equal Chords):
प्रमेय (Theorem):10.6.एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र से (या केन्द्रों से) समान दूरी पर होती हैं।
दिया है (Given):एक वृत्त,जिसका केन्द्र O है और जीवा AB=जीवा CD है।तथा OP \perp AB और OQ \perp CD
सिद्ध करना है (To Prove):OP=OQ
रचना (Construction):OB और OC को मिलाया।
उपपत्ति (Proof):केन्द्र से जीवा पर लम्ब जीवा को समद्विभाजित करता है।
\therefore BP=\frac{1}{2} AB और CQ=\frac{1}{2} CD
परन्तु AB=CD (दिया है)
\therefore BP=CQ
अब \triangle OPB और \triangle OQC में
OB=OC (एक ही वृत्त की त्रिज्याएँ)
\angle OPB=\angle OQC=90^{\circ}
BP=CQ (सिद्ध किया है)
RHS सर्वांगसमता गुणधर्म से
\triangle OPB \cong \triangle OQC
अतः OP=OQ (CPCT से)
प्रमेय (Theorem):10.7.एक वृत्त के केन्द्र से समदूरस्थ जीवाएँ लम्बाई में समान होती है।
दिया है (Given):एक वृत्त जिसका केन्द्र O है।AB और CD दो जीवाएँ हैं।OP \perp AB और OQ \perp CD और OP=OQ
सिद्ध करना है (To Prove):AB=CD
रचना (Construction):OA और OC को मिलाया।
उपपत्ति (Proof):\triangle OAP और \triangle OCD में
OA=OC (एक ही वृत्त की त्रिज्याएँ)
OP=OQ (दिया है)
\angle OPA=\angle OQC=90^{\circ}
RHS सर्वांगसमता गुणधर्म से
\triangle OAP \cong \triangle OCD \\ \therefore AP=CQ (CPCT से)
केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
\therefore AP=\frac{1}{2} AB और CQ=\frac{1}{2} CD \cdots(2)
(1) और (2) से:
AB=CD
3.समान जीवाएँ और उनकी केन्द्र से दूरियाँ के उदाहरण (Equal Chords and Distances From Centre Examples):
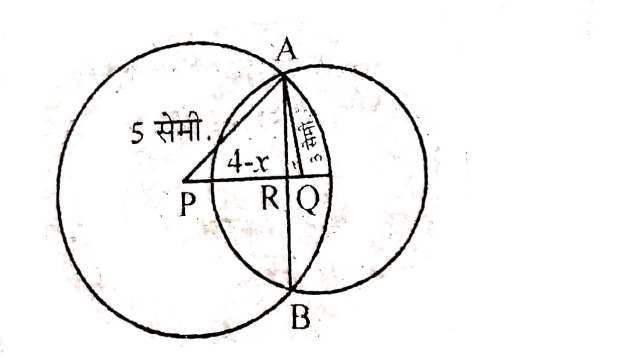
Example:1.5 cm और 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है।उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
Solution:AP=5 सेमी,AQ=3 सेमी
माना QR=x तथा PR=4-x
अब समकोण \triangle ARP में
AR^2=A P^2-P R^2 \\ =5^2-(4-x)^2 \\=25-\left(16-8 x+x^2\right) \\ =25-16+8 x-x^2 \\ \Rightarrow A R^2=9+8 x-x^2 \cdots(1)
समकोण \triangle ARQ में
AR^2 =A Q^2-Q R^2 \\ =3^2-x^2 \\ \Rightarrow A R^2=9-x^2 \ldots(2)
(1) व (2) से:
9+8 x-x^2=9-x^2 \\ \Rightarrow 8 x=0 \Rightarrow x=0
अतः Q व R सम्पाती है फलतः AR=3 सेमी
AB=2×AR=2×3=6 सेमी
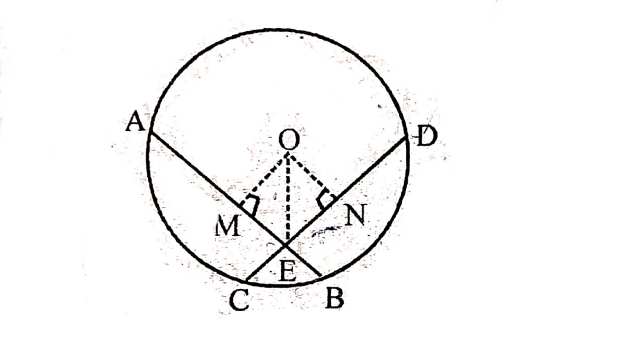
Example:2.यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें,तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।
Solution:दिया है (Given):एक वृत्त, जिसका केन्द्र O है।जीवा AB=जीवा CD है जो कि E पर प्रतिच्छेद करती है। O M \perp A B, ON \perp CD और OE को मिलाया गया है।
सिद्ध करना है (To Prove):AE=DE और CE=BE
उपपत्ति (Proof):\triangle OME और \triangle ONE में
OE=OE (उभयनिष्ठ है)
OM=ON
(समान जीवाएँ केन्द्र से समदूरस्थ होती हैं)
\angle OME=\angle ONE=90^{\circ}
RHS सर्वांगसमता गुणधर्म से
\triangle OME \cong \triangle ONE
ME=NE (CPCT से)…. (1)
AM=\frac{1}{2} AB तथा DN=\frac{1}{2} CD \ldots(2)
(केन्द्र से जीवा पर लम्ब,जीवा को समद्विभाजित करता है)
परन्तु AB=CD (दिया है)…. (3)
(2) व (3) से:
AM=DN ….. (4)
(1) व (4) को जोड़ने पर:
ME+AM=NE+DN
\Rightarrow AE=DE
इसी प्रकार CE=BE
Example:3.यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें,तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
Solution:दिया है (Given):एक वृत्त, जिसका केन्द्र O है, में जीवा AB=जीवा CD जो कि E पर प्रतिच्छेद करती हैं।OE को मिलाया गया है।
सिद्ध करना है (To Prove): \angle OEA=\angle OED
रचना (Construction): OM \perp AB और ON \perp CD खींचा।
उपपत्ति (Proof):\triangle OME और \triangle ONE में
OE=OE (उभयनिष्ठ है)
OM=ON
(बराबर जीवाएँ केन्द्र से समदूरस्थ होती हैं)
\angle OME=\angle ONE=90^{\circ}
RHS सर्वांगसमता गुणधर्म से
\triangle OME \cong \triangle ONE \\ \angle OEM=\angle OEN (CPCT से)
\Rightarrow \angle OEA=\angle OED
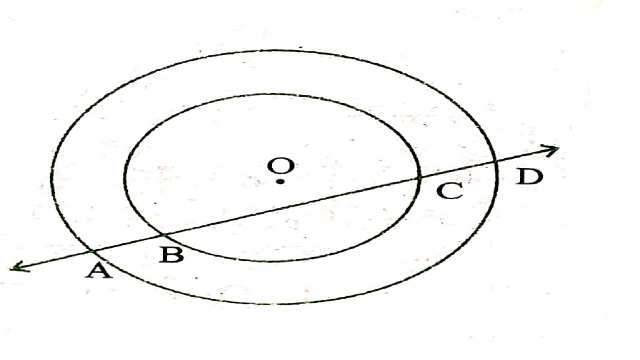
Example:4.यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है,A,B,C और D पर प्रतिच्छेद करे,तो सिद्ध कीजिए AB=CD है (देखिए आकृति)।
Solution:दिया है (Given):दो संकेन्द्रीय वृत्त जिनका केन्द्र O है।एक रेखा इन दो वृत्तों को A,B,C और D पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove):AB=CD
रचना (Construction): OM \perp BC खींचा।
उपपत्ति (Proof):चूँकि BC छोटे वृत्त की एक जीवा है और OM \perp BC
\therefore BM=CM ….. (1)
(केन्द्र से जीवा पर लम्ब,जीवा को समद्विभाजित करता है।)
पुनः AD बड़े वृत्त की एक जीवा है और OM \perp AD
\therefore AM=DM …… (2)
(केन्द्र से जीवा पर लम्ब इसे समद्विभाजित करता है।)
(2) में से (1) घटाने पर:
AM-BM=DM-CM
\Rightarrow AB=CD
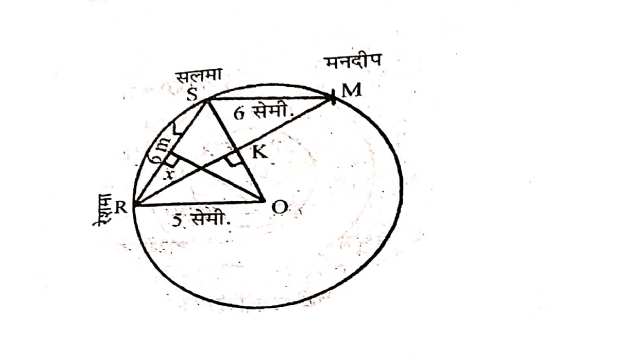
Example:5.एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा,सलमा एवं मनदीप खेल रही हैं।रेशमा एक गेंद को सलमा के पास,सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है।यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो,तो रेशमा और मनदीप के बीच दूरी क्या है?
Solution:रेशमा,सलमा और मनदीप को क्रमशः बिन्दु R,S और M द्वारा दर्शाया।माना OK=x,OR=OS=5 m,OS-OK=5-x
समकोण \triangle RKS में
RK^2=RS^2-KS^2 \\ =6^2-(5-x)^2 \\=36-\left(25-10 x+x^2\right) \\=36-25+10 x-x^2 \\ \Rightarrow R k^2=11+10 x-x^2 \ldots(1)
समकोण \triangle RKO में
RK^2=OR^2-OK^2=5^2-x^2=25-x^2 \cdots(2)
(1) व (2) से:
11+10 x-x^2=25-x^2 \\ \Rightarrow 10 x=14 \Rightarrow x=1.4
(2) में रखने परः
RK^2=25-(1.4)^2=25-1.96=23.04 \\ \Rightarrow R K=\sqrt{23.04}=4.8 m
अतः RM=2×RK=2×4.8=9.6 m
Example:6.20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है।तीन लड़के अंकुर,सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हुए हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है।प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
Solution:माना AB=BC=CA=x मीटर
रचना (Construction): AOD \perp BC खींची।
अब BD=\frac{x}{2}, O D=\frac{20}{2}=10
पाइथागोरस प्रमेय से:
OD^2=O B^2-B D^2 \\ \Rightarrow 10^2 =20^2-\left(\frac{x}{2}\right)^2 \\ \Rightarrow 100=400-\frac{x^2}{4} \\ \Rightarrow \frac{x^2}{4}=300 \\ \Rightarrow x^2=1200 \\ \Rightarrow x=\sqrt{1200} \\ \Rightarrow x=20 \sqrt{3}
अतः प्रत्येक फोन की डोरी की लम्बाई=20 \sqrt{3} मीटर
उपर्युक्त उदाहरणों के द्वारा समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Equal Chords and Distances From Centre),समान जीवाएँ और उनकी केन्द्र से दूरियाँ कक्षा 9 (Equal Chords and Distances From Their Centre Class 9) को समझ सकते हैं।
4.समान जीवाएँ और उनकी केन्द्र से दूरियाँ पर आधारित सवाल (Questions Based on Equal Chords and Distances From Centre):
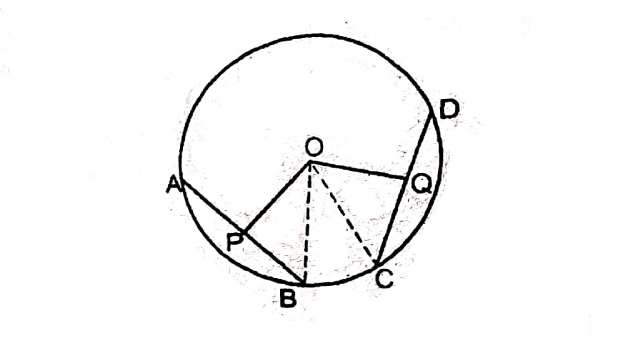
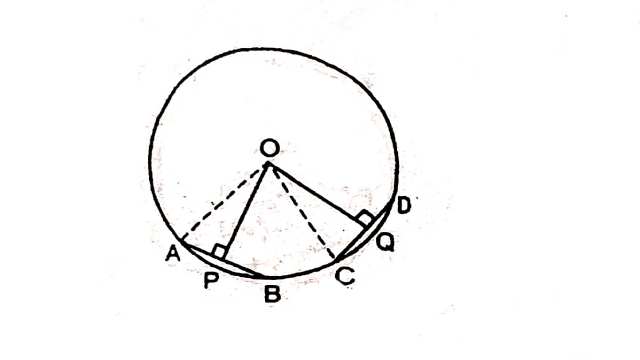
(1.)आकृति में,AB=CB और O वृत्त का केन्द्र है।सिद्ध कीजिए कि \angle ABC का समद्विभाजक BO है।
(2.)चित्र में AB और AC वृत्त की दो समान जीवाएँ हैं।O वृत्त का केन्द्र है।यदि OD \perp AB और OE \perp AC हो,तो सिद्ध कीजिए कि ADE एक समद्विबाहु त्रिभुज है।
उपर्युक्त सवालों को हल करने पर समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Equal Chords and Distances From Centre),समान जीवाएँ और उनकी केन्द्र से दूरियाँ कक्षा 9 (Equal Chords and Distances From Their Centre Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Area of Triangles and Parallelograms
5.समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Frequently Asked Questions Related to Equal Chords and Distances From Centre),समान जीवाएँ और उनकी केन्द्र से दूरियाँ कक्षा 9 (Equal Chords and Distances From Their Centre Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.वृत्त किसे कहते हैं? (What is a Circle?):
उत्तर:एक तल पर उन सभी बिन्दुओं का समूह,जो तल के एक स्थिर बिन्दु से एक स्थिर दूरी पर स्थित हों,एक वृत्त कहलाता है।
प्रश्न:2.वृत्त की त्रिज्या किसे कहते है? (What is the Radius of a Circle?):

उत्तर:स्थिर बिन्दु को वृत्त का केन्द्र (Centre) कहते हैं तथा स्थिर दूरी को वृत्त की त्रिज्या (radius) कहते हैं।
प्रश्न:3.दीर्घचाप और लघुचाप किसे कहते हैं? (What is Manor Arc and Minor Arc?):
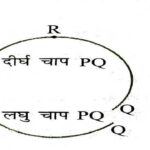
उत्तर:दो बिन्दुओं के बीच वृत्त के भाग को,एक चाप (arc) कहते हैं।आकृति में बिन्दुओं P तथा Q के बीच के वृत्त के भागों को देखिए।आप पाएंगे कि दोनों भागों में से एक बड़ा है तथा एक छोटा है।लघुचाप PQ को \overset{\frown}{PQ} से व्यक्त करते हैं तथा दीर्घचाप को PQ को \overset{\frown}{PRQ} से,जहाँ R चाप पर P तथा Q के बीच कोई बिन्दु है।
उपर्युक्त प्रश्नों के उत्तर द्वारा समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Equal Chords and Distances From Centre),समान जीवाएँ और उनकी केन्द्र से दूरियाँ कक्षा 9 (Equal Chords and Distances From Their Centre Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Equal Chords and Distances From Centre
समान जीवाएँ और उनकी केन्द्र से दूरियाँ
(Equal Chords and Distances From Centre)
Equal Chords and Distances From Centre
समान जीवाएँ और उनकी केन्द्र से दूरियाँ (Equal Chords and Distances From Centre) के
बारे में अध्ययन करेंगे।समान जीवाओं की केन्द्र से दूरियों को प्रमेय व उदाहरणों द्वारा समझेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.