Conformal Mapping in Complex Analysis
1.सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Conformal Mapping in Complex Analysis),अनुकोण प्रतिचित्रण (Conformal Mapping):
सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Conformal Mapping in Complex Analysis) के इस आर्टिकल में z-समतल से w-समतल में प्रतिचित्रण का विवेचन किया गया है।अब यदि w,z का एक वैश्लेषिक फलन है तब w-समतल में w के मानों को बिन्दुओं से निरूपित करते हैं इनके समवर्ती z के मानों को z-समतल में बिन्दुओं से निरूपित करते हैं।इसको दूसरे शब्दों में यह भी कहते हैं कि w-समतल का बिन्दु z-समतल के अपने समवर्ती बिन्दु को निरूपित करता है और व्यापक रूप से z-समतल के प्रदेश (Domain) w-समतल के अपने समवर्ती प्रदेश द्वारा मान चित्रित होते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Convergence of Series Complex Analysis
2.सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण पर आधारित उदाहरण (Examples Based on Conformal Mapping in Complex Analysis):
Example:1.प्रदर्शित कीजिए कि w=2 z-z^2 डिस्क \left|z\right|<1 के w-क्षेत्रफल के क्षेत्र D में अनुकोण प्रतिचित्रण करता है।
(Show that w=2 z-z^2 maps the disc \left|z\right|<1 conformally onto a region D in the w-plane.)
Solution: w=2z-z^2 \\ \Rightarrow w=2(x+i y)-(x+i y)^2 \\ =2 x+2 i y-\left(x^2-y^2+2 i x y\right) \\ w=2 x-x^2+y^2+i(2 y-2 x y) \\ \Rightarrow u+i v=2 x-x^2+y^2+i(2y-2xy) \\ u=2 x-x^2+y^2, v=2 y-2 x y \\ \frac{\partial u}{\partial x}=2-2 x, \frac{\partial v}{\partial y}=2-2 x, \frac{\partial v}{\partial x}=-2 y, \frac{\partial u}{\partial y}=2 y
अतः \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}, \frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}
जो कि कोशी-रीमान समीकरण हैं।अतः w वैश्लेषिक है फलतः रूपान्तरण w अनुकोणीय है।
Example:3.उन बिन्दुओं को प्राप्त कीजिए जहाँ प्रतिचित्रण f(z)=3 z+z^2 अनुकोणी नहीं है।
(Find the points where the mapping f(z)=3 z+z^2 is not conformal.)
Solution: f(z)=3 z+z^2 \\ \frac{d f(z)}{d z}=3+2 z \\ \frac{d f(z)}{d z}=0 सेः
z+2 z=0 \\ z=-\frac{3}{2}
Example:4.दिया हुआ है कि एक त्रिभुज के जिसके शीर्ष 3+4i,-3-4i तथा – 5i हैं।निम्न रूपान्तरणों के अन्तर्गत प्रतिबिम्ब ज्ञात करियेः
(Given a triangle with vertices at 3+4i,-3-4i and – 5i,find the images for the transformation):
Example:4(i).w=z+5i
Solution:w=z+5i
z=3+4i
w=3+4i+5i=3+9i
z=-3-4i
w=-3-4i+5i=-3+i
z=-5i
w=-5i+5i=0
3+9i,-3+i,0
Example:4(ii).w=iz+(2-i)
Solution:w=iz+(2-i)
z=3+4i
w=i(3+4i)+(2-i)
w=3i-4+2-i
w=-2+2i
z=-3-4i
w=i(-3-4i)+(3-i)
=-3i+4+2-i
w=6-4i
z=-5i
w=i(-5i)+(2-i)
=5+2-i
w=7-i
-2+2i,6-4i,7-i
Example:4(iii).w=(2+i)z-3
Solution:w=(2+i)z-3
z=3+4i
w=(2+i)(3+4i)-3
=6+11i-4-3
w=-1+11i
z=-3-4i
w=(2+i)(-3-4i)-3
=-9-11i+4
w=-5-11i
z=-5i
w=(2+i)(-5i)-3
=-10i+5-3
w=2-10i
-1+11i,-5-11i,2-10i
Example:5.प्रदर्शित करिए कि दोनों रूपान्तरण
w=\frac{z+i}{z-i} और w=\frac{i+z}{i-z} \\ |W| \leq 1 को निम्न अर्धतल I(z) \leq 0 में रूपान्तरित करता है।
(Show that both the transformations
w=\frac{z+i}{z-i} and w=\frac{i+z}{i-z}
transform |W| \leq 1 into the lower half plane I(z) \leq 0)
Solution: w=\frac{i+i}{z-i} \\ \overline{w}=\frac{\overline{z+i}}{\overline{z-i}}=\frac{\bar{z}-i}{\bar{z}+i} \\ w \overline{w}-1 =\frac{z+i}{z-i} \cdot \frac{\bar{z}-i}{\bar{z}+i}-1 \\ =\frac{z \bar{z}-i z+i z-i^2-(z \bar{z}+z i-i \bar{z}-i^{2})}{\mid z-i\mid^2} \\ =\frac{-2 i z+2 i \bar{z}}{\mid z-i \mid^2} \\ =\frac{2 i(\bar{z}-z)}{|z-i|^2} \\ =\frac{2 i(-2 i y)}{|z-i|^2}=\frac{4 y}{|z-i|^2}=\frac{4 I(z)}{|z-i|^2}
इसी प्रकार w=\frac{i+z}{i-z} से
|w|^2-1=\frac{4 y}{|z-1|^2} \quad\left[ \because I(z)=y \right]
(i) जब |w|=1 तब y=0 अर्थात् z-समतल का वास्तविक अक्ष
(ii) |w|<1 तब y<0 अर्थात् z-समतल निम्न अर्धतल इस प्रकार |W| \leq 1 को निम्न अर्धतल I(z) \leq 0 में रूपान्तरित करता है।
Example:6.प्रदर्शित करिए कि दोनों रूपान्तरण w=\frac{1+z}{1-z} तथा w=\frac{z+1}{z-1} को अर्धतल में रूपान्तरित करता है। (Show that both the transformations w=\frac{1+z}{1-z} and w=\frac{z+1}{z-1} transform |W| \leq 1 into the half plane Re(z) \leq 0)
Solution: w=\frac{1+z}{1-z} \\ \bar{w} =\frac{\overline{1+z}}{1-z}=\frac{1+\bar{z}}{1-\bar{z}} \\ w \bar{w}-1 =\frac{1+z}{1-\bar{z}} \cdot \frac{1+\bar{z}}{1-\bar{z}}-1 \\ =\frac{1+\bar{z}+z+z \bar{z}-(1-\bar{z}-z+z \bar{z})}{|1-z|^2} \\ =\frac{2(z+\bar{z})}{\mid 1-z \mid^2} \\ \Rightarrow \left|w^2\right|-1 =\frac{4 \cdot \operatorname{Re}(z)}{|1-z|^2}
इसी प्रकार w=\frac{z+1}{z-1} सेः
|w|^2-1=\frac{4 x}{|1-z|^2}=\frac{4 Re(z)}{|1-z|^2} \left[\because \operatorname{Re}(z)=x \right](i)जब |w|=1 तब x=0 अर्थात् z-समतल का काल्पनिक अक्ष
(ii)जब |w|<1 तब x<0 अर्थात् Re(z) \leq 0 अतः z-समतल बायां अर्धतल
Example:7.रूपान्तरण w=i \frac{1-z}{1+z} के अन्तर्गत प्रदर्शित करिए कि वृत्त |z|=1 के भीतरी भाग का निरूपण w-समतल में वास्तविक अक्ष के ऊपर का तल,ऊपरी अर्धवृत्त का धन अर्ध-वास्तविक अक्ष तथा निम्न अर्धवृत्त का ऋणात्मक अर्ध वास्तविक अक्ष में रूपान्तरित होते हैं। (In the transformation w=i \frac{1-z}{1+z}, show that the interior of the circle |z|=1 is represented in the w-plane by the plane above the real axis, the upper semi-circle into positive half or real axis and lower semi-circle into negative half of the real axis.)
Solution: w=i \frac{1-z}{1+z} \\ \Rightarrow u+i v=i \frac{(1-x-i y)}{1+x+i y} \\ =\frac{i-i x+y}{1+x+i y} \times \frac{1+x-i y}{1+x-i y} \\ \Rightarrow u+i v=\frac{2 y-i\left(x^2+y^2-1\right)}{(1+x)^2+y^2} \\ \Rightarrow u=\frac{2 y}{(1+x)^2+y^2}, v=-\frac{\left(x^2+y^2-1\right)}{(1+x)^2+y^2}
v=0 के संगत x^2+y^2-1=0 \Rightarrow |z|=1
z-समतल में ऊपरी अर्धवृत्त में y धनात्मक है अतः u धनात्मक है अर्थात् w-समतल में वास्तविक अक्ष के ऊपर का तल। पुनः z-समतल का निम्न अर्धवृत्त, y धनात्मक है और u ऋणात्मक है अर्थात् w-समतल के वास्तविक अक्ष का ऋणात्मक अर्धतल। |z|=1, x^2+y^2<1 अर्थात् x^2+y^2=1 ऋणात्मक है तथा v धनात्मक है अर्थात् w-समतल के वास्तविक अक्ष का ऊपरी अर्धतल में रूपान्तरित होता है।
Example:8.रूपान्तरण w=\frac{i z+1}{z+i} को z-समतल में वृत्त |z|=1 के अन्तः एवं बाहरी भाग की प्रतिचित्रण प्राप्त करने के लिए विवेचन कीजिए। (Discuss the application of the transformation w=\frac{i z+1}{z+i} to the areas in the z-plane which are respectively inside and outside the circle |z|=1)
Solution: w=\frac{i z+1}{z+i} \\ \Rightarrow u+i v =\frac{i(x+i y)+1}{x+i y+i} \\ =\frac{i(x+i y)+1}{x+i(1+y)} \cdot \frac{x-i(1+y)}{x-i(1+y)} \\ \Rightarrow u+i v=\frac{2 x+i \left(x^2+y^2-1\right)}{x^2+(1+y)^2}
तुलना करने परः v=\frac{x^2+y^2-1}{x^2+(1+y)^2}=\frac{|z|^{2}-1}{x^2+(1+y)^2}
जब v=0 अर्थात् |z|=1 इकाई वृत्त की सीमा v>0 अर्थात् w-समतल के ऊपरी तल के संगत |z| >1 अर्थात् |z| =1 का बाहरी भाग
v<0 अर्थात् w-समतल का निम्न अर्धतल के संगत |z|<1 अर्थात् वृत्त |z|=1 के अन्दर का भाग।
Example:10.सिद्ध कीजिए कि रूपान्तरण w=\frac{5-4 z}{4 z-2} वृत्त |z|=1 को w-समतल में इकाई त्रिज्या के वृत्त में रूपान्तरित करता है।
(Prove that the transformation w=\frac{5-4 z}{4 z-2} transform the circle |z|=1 into a circle of radius unity in the w-plane):
Solution: w=\frac{5-4 z}{4 z-2} \\ \Rightarrow 4 w z-2 w=5-4 z \\ \Rightarrow 4 w z+4 z=5+2 w \\ \Rightarrow z=\frac{5+2 w}{4(w+1)} \\ \mid z \mid^2=z \bar{z}=1 \\ z \bar{z}=\frac{5+2 w}{4(w+1)} \cdot \frac{5+2 \bar{w}}{4(\bar{w}+1)} \\ \Rightarrow 1=\frac{4 w \bar{w}+10(w+\bar{w})+25}{16[w \bar{w}+(w+\bar{w})+1]} \\ \Rightarrow 4 w \bar{w}+10(w+\bar{w})+25=16[w \bar{w}+(w+\bar{w})+1] \\ \Rightarrow 12 w \bar{w}+6(w+\bar{w})-9=0 \\ \Rightarrow 12\left(u^2+v^2\right)+6 \times 2 u-9=0 \\ \Rightarrow u^2+v^2+u-\frac{3}{4}=0
यह एक वृत्त की समीकरण है जिसका केन्द्र \left(-\frac{1}{2}, 0\right) तथा त्रिज्या=\sqrt{\left(\frac{1}{2}\right)^2+0^2+\frac{3}{4}}=1 अर्थात् इकाई
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Conformal Mapping in Complex Analysis),अनुकोण प्रतिचित्रण (Conformal Mapping) को समझ सकते हैं।
3.सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण के सवाल (Conformal Mapping in Complex Analysis Questions):
(1.)सिद्ध करो कि रूपान्तरण w=\frac{2 z+3}{z-4} में वृत्त का x^2+y^2-4 x=0 रूपान्तरण सरल रेखा 4u+3=0 में करता है तथा स्पष्ट करें कि वृत्त में रूपान्तर क्यों नहीं होता है?
(Show that the transformation w=\frac{2 z+3}{z-4} transform the circle x^2+y^2-4 x=0 into straight line 4u+3=0 and explain why the curve is not a circle)
(2.)सिद्ध करों कि दोनों रूपान्तरण
w=\frac{1-z}{1+z} तथा w=\frac{z-1}{z+1}
|w| \leq 1 को अर्द्धतल Re(z) \geq 1 में रूपान्तरित करता है।
(Show that both the transformation
w=\frac{1-z}{1+z} and w=\frac{z-1}{z+1}
transform |w| \leq 1 into half plane Re(z) \geq 1.)
उपर्युक्त सवालों को हल करने पर सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Conformal Mapping in Complex Analysis),अनुकोण प्रतिचित्रण (Conformal Mapping) को ठीक से समझ सकते हैं।
Also Read This Article:-Analytic Functions in Complex Analysis
4.सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Frequently Asked Questions Related to Conformal Mapping in Complex Analysis),अनुकोण प्रतिचित्रण (Conformal Mapping) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सम्मिश्र विश्लेषण में रूपान्तरण या प्रतिचित्रण से क्या तात्पर्य है? (What Do You Mean Transformation or Mapping in Complex Analysis?):
उत्तरःयदि वास्तविक चर x का वास्तविक फलन f(x) हो तो y=f(x),x-अक्ष एवं y-अक्ष के बिन्दुओं के मध्य संगति (correspondence) स्थापित करता है।इस सम्बन्ध को हम xy-तल में वक्र द्वारा निरूपित कर सकते हैं।परन्तु जब f(z) सम्मिश्र चर राशि z का सम्मिश्र फलन है तो w=f(z) के लिये ऐसा कोई सुविधाजनक आलेखी निरूपण सम्भव नहीं है।क्योंकि प्रत्येक सम्मिश्र चरों w एवं z के लिए एक समतल की आवश्यकता होती है।इसके बावजूद फलन w=f(z) के संगत बिन्दुओं z=x+iy एवं w=u+iv के समुच्चयों को दो अलग-अलग समतलों जिन्हें क्रमशः z तथा w-समतल कहते हैं,पर प्रदर्शित करके फलन के बारे में कुछ जानकारी प्राप्त की जा सकती है।
माना कि w=f(z)=u+iv जहाँ u=u(x,y) तथा v=v(x,y)…. (1)
अब f के प्रान्त D में z-समतल के प्रत्येक बिन्दु के संगत w-समतल में एक बिन्दु (u,v) विद्यमान होगा।z-समतल एवं w-समतल के बिन्दुओं के मध्य समीकरणों (1) से परिभाषित संगति को प्रतिचित्रण या रूपान्तरण कहते हैं तथा इन दो समतलों में संगत बिन्दुओं के समुच्चय को एक-दूसरे का प्रतिबिम्ब (Image) कहते हैं।
प्रश्न:2.अनुकोण प्रतिचित्रण की परिभाषा दीजिए। (Define the Conformal Mapping):
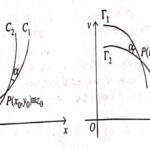
उत्तर:माना कि रूपान्तरण u=u(x,y),v=v(x,y) के अन्तर्गत z-समतल का बिन्दु P\left(x_0, y_0\right) [माना \left(x_0, y_0\right)=z_0 ] w-समतल के बिन्दु p^{\prime}\left(u_0, v_0\right) [माना \left(u_0, v_0\right)=w_0 ] पर प्रतिचित्रत होता है।माना कि अवकलनीय चापों C_1 तथा C_2 का प्रतिच्छेदन बिन्दु है।अब बिन्दु w-समतल का बिन्दु p^{\prime}\left(w_0\right) का समवर्ती है।साथ ही यह भी माना कि वक्र C_1 पर Z_1 तथा C_2 वक्र पर Z_2 कोई बिन्दु है तथा w_1 एवं w_2 क्रमशः \Gamma_1 तथा \Gamma_2 के समवर्ती बिन्दु है।माना w_1 तथा w_2 क्रमशः वक्र \Gamma_1 तथा \Gamma_2 की रचना करते हैं अर्थात् वक्र C_1 तथा C_2 क्रमशः वक्र \Gamma_1 तथा \Gamma_2 पर प्रतिचित्रत होते हैं और \Gamma_1 तथा \Gamma_2 का प्रतिच्छेदन बिन्दु p^{\prime}\left(w_0\right) है।तब यदि रूपान्तरण इस प्रकार है कि वक्र C_1 तथा C_2 के मध्य का कोण p\left( z_{0} \right) पर \Gamma_1 तथा \Gamma_2 वक्र तथा के मध्य कोण p^{\prime}\left(w_0\right) पर समान है।साथ में यदि दोनों समतलों पर दोनों चित्रों में कोण की एक अभिदिशा है तब ऐसे रूपान्तरण अथवा प्रतिचित्रण को अनुकोण निरूपण कहते हैं।
प्रश्न:3.अनुकोण प्रतिचित्रण के लिए पर्याप्त प्रतिबन्ध क्या है? (What are the Sufficient Conditions for Conformal Mapping?):
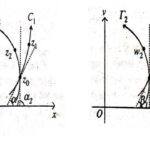
उत्तर:प्रमेय (Theorem):माना f(z),z का एक विश्लेषिक फलन z-समतल के प्रदेश D में है तथा यह भी माना कि D में f^{\prime}(z) \neq 0 तब प्रतिचित्रण w=f(z), प्रदेश D के प्रत्येक बिन्दु पर अनुकोण है।
(Let f(z) be an analytic function of z in a region D of the z-plane and let f^{\prime}(z) \neq 0 in D.Then the mapping w=f(z) is conformal at all points of D.)
उपपत्ति (Proof):माना कि z-समतल में दो अवकलनीय वक्र C_1 तथा C_2 हैं जिनका प्रतिच्छेदन बिन्दु z_{0} है तथा इस बिन्दु z_{0} पर दो निश्चित स्पर्श रेखाएँ हैं जो वास्तविक अक्ष के साथ \alpha_1 तथा \theta_2 कोण बनाती हैं।माना कि z_1 और z_2 वक्र C_1 तथा C_2 पर z_{0} के निकट दो बिन्दु इस प्रकार हैं z_1 और z_2 बिन्दु z_{0} से समान दूरी r है (जहाँ r अति अल्प संख्या है)।इसलिए
z_1-z_0=r e^{i \theta_{1}} , z_2-z_0=r e^{i \theta_2} साथ ही तब,जब r \rightarrow 0 तो \theta_1 \rightarrow \alpha_1 तथा \theta_2 \rightarrow \alpha_2
माना कि के समवर्ती बिन्दु w-समतल पर एक बिन्दु w_{0} है और बिन्दु z_1 और z_2 के समवर्ती क्रमशः बिन्दु w_1 तथा w_2 हैं।अब कोई बिन्दु वक्र के अनुदिश z_{0} से z_{1} को गमन करता है तो उसका प्रतिबिम्ब बिन्दु w-समतल में \Gamma_1 वक्र के अनुदिश w_{0} से w_{1} को गमन करता है।इसी प्रकार जब कोई बिन्दु वक्र c_{2} के अनुदिश z_{0} से z_{2} गमन करता है तो उसका प्रतिबिम्ब w-समतल में वक्र \Gamma_2 के अनुदिश w_{0} से w_{2} को गमन करता है।
माना w_1-w_0=\lambda_1 e^{i \phi_1} ; w_2-w_0=\lambda_{2} e^{i \phi_2}
चूँकि f(z),बिन्दु z_{0} पर विश्लेषित है अतः f^{\prime}\left(z_0\right) विद्यमान है।
अब विश्लेषिक फलन की परिभाषा के अनुसार
f^{\prime}\left(z_0\right)=\lim_{z_1 \rightarrow z_{0}} \frac{f\left(z_1\right)-f\left(z_0\right)}{z_1-z_0} \\ =\lim_{z_1 \rightarrow z_0} \frac{w_1-w_0 }{z_1-z_0} \\ \Rightarrow \lambda e^{i \phi}=\lim_{r \rightarrow 0} \frac{\lambda_1 e^{i \phi_1}}{r e^{i \theta_1}}
[ \because f^{\prime}\left(z_0\right) \neq 0 तथा w-समतल में माना कि f^{\prime}\left(z_0\right)=\lambda e^{i \phi} ]
\Rightarrow \lambda=\lim \frac{\lambda_{1}}{r}=\mid f^{\prime}\left(z_0\right) \mid तथा \lim \left(\phi_{1}-\theta_1\right)=\phi
या \beta_1-\alpha_1=\phi या \beta_1=\alpha_1+\phi
इसी प्रकार सिद्ध कर सकते हैं कि
\beta_2=\alpha_2+\phi
इससे हम देखते हैं कि वक्र \Gamma_1 तथा \Gamma_2 के प्रतिच्छेदन बिन्दु w_{0} पर निश्चित स्पर्श रेखाएँ हैं जो वास्तविक अक्ष के साथ क्रमशः \alpha_{1}+\phi तथा \alpha_{2}+\phi कोण बनाती हैं और इसलिए वक्र \Gamma_1 तथा \Gamma_2 के मध्य बिन्दु w_{0} पर कोण \beta_2-\beta_1=\alpha_2-\alpha_1 है।
अतः वक्र \Gamma_1 तथा \Gamma_2 का प्रतिच्छेदन वही है जो वक्र C_{1} तथा C_{2} का है इसके अतिरिक्त दोनों कोणों की एक ही अभिदिशा है।
उपर्युक्त दोनों कोणों के कारण रूपान्तरण w=f(z) अनुकोण प्रतिचित्रण करता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Conformal Mapping in Complex Analysis),अनुकोण प्रतिचित्रण (Conformal Mapping) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Conformal Mapping in Complex Analysis
सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण
(Conformal Mapping in Complex Analysis)
Conformal Mapping in Complex Analysis
सम्मिश्र विश्लेषण में अनुकोण प्रतिचित्रण (Conformal Mapping in Complex Analysis) के
इस आर्टिकल में z-समतल से w-समतल में प्रतिचित्रण का विवेचन किया गया है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








