1.आप सम्मिश्र परिरेखा (कन्टूर) समाकलन को कैसे हल करते हैं?(How do you Solve Complex Contour Integration?),परिरेखा (कन्टूर) समाकलन (Contour Integration)-

सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) के लिए हम अवशेष कलन की विधियों के प्रयोग से वास्तविक निश्चित समाकलों के मूल्यांकन का विवेचन एवं निरूपण करेंगे।कोशी अवशेष प्रमेय की सहायता से वास्तविक निश्चित समाकलों का मूल्यांकन आसानी से किया जा सकता है।इसके लिए उचित परिरेखा का चयन इस प्रकार करते हैं कि फलन की समस्त विचित्रताएं C के अन्दर रहे।इन विचित्र बिन्दुओं पर अवशेष का मूल्यांकन करें तथा कोशी अवशेष प्रमेय का उपयोग करके समाकलन का मूल्यांकन करते हैं।
(1.)\int_{0}^{2 \pi} f(\cos \theta, \sin \theta) d \theta प्रकार के समाकलन का मूल्यांकन-
यहां हम मानकर चलते हैं कि f(\cos \theta, \sin \theta) , \cos \theta \text{ व } \sin \theta के बहुपदों का परिमेय फलन है तथा समाकलन की सीमाओं में परिबद्ध फलन है।
इस प्रकार के समाकलों के मूल्यांकन के लिए परिरेखा C मूलबिन्दु के केन्द्रित इकाई त्रिज्या का वृत्त लेते हैं।C पर स्थित किसी भी z के लिए

|z|=1 \Rightarrow z=e^{i \theta}, d z=i e^{i \theta}  d \theta=\frac{d z}{iz}
इन मानों को समाकलन में प्रतिस्थापित करने पर-

\int_{0}^{2 \pi} f(\cos \theta, \sin \theta) d \theta=\int_{C} F(z) d z
प्राप्त करते हैं, यहां यह F(z) परिमेय फलन है जिसकी C पर कोई विचित्रता नहीं है। अतः कोशी अवशेष प्रमेय के अनुसार

\int_{c} f(z) d z=2 \pi i \sum R^{+}
यहां पर \sum R^{+} वृत्त के अन्दर स्थित F(z) की विचित्रताओं के अवशेषों का योग है।
(2.)परिरेखा समाकलन सम्बन्धित प्रमेय (Theorem Related with Contour Integration)-
प्रमेय (Theorem):1.मान लें कि AB वृत्त |z-a|=r का चाप \alpha \leq \theta<\beta है।यदि \lim _{z \rightarrow a}(z-a) f(z)=k तथा k अचर राशि है तो

\lim _{r \rightarrow 0} \int_{A B} f(z) d z=i(\beta-\alpha) k
यहां AB पर समाकलन वामावर्त दिशा में किया गया है।
(Let AB the arc \alpha \leq \theta<\beta of the circle |z-a|=r,If

\lim _{r \rightarrow 0} \int_{A B} f(z) d z=i(\beta-\alpha) k
the integration along AB is taken along anticlockwise direction.)
उपपत्ति (Proof):चूंकि \lim _{z \rightarrow a}(z-a) f(z)=k इसलिए किसी वास्तविक संख्या के लिए इस प्रकार कि संख्या प्राप्त की जा सकती है कि
|(z-a) f(z)-k|<\varepsilon जब भी |z-a|<r
अर्थात् \varepsilon \rightarrow 0 यथा z \rightarrow a \text { तथा } r \rightarrow 0 मान लें कि

(z-a) \cdot f(z)-k=\eta(z)
यहां पर |z-a|<r के लिए \mid \eta(z) <\epsilon तो

f(z)=\frac{k+\eta(z)}{z-a}
अतः \int_{A B} f(z) d z =\int_{A B} \frac{K+\eta(z)}{z-a} d z \\ =K \int_{\alpha}^{\beta} \frac{i r e^{i \theta} d \theta}{r e^{i \theta}}+\int_{A B} \frac{\eta(z)}{z-a} d z   \because AB \text{ पर } z-a=r i e^{i \theta}

=K i(\beta-\alpha)+\int_{A B} \frac{\eta (z)}{z-a} d z
अब \left|\int_{A B} f(z) d z-K i(\beta-\alpha)\right|=\left|\int_{A B} \frac{\eta(z)}{z-a} d z\right|<\varepsilon(\beta-\alpha) \rightarrow 0
यथा \varepsilon \rightarrow 0
इस प्रकार \lim _{x \rightarrow 0} \int_{A B} f(z) d z=i(B-\alpha) k
प्रमेय (Theorem):2.मान लें कि AB वृत्त |z|=R का चाप \alpha \leq \theta \leq \beta है।यदि \lim _{z \rightarrow \infty} z f(z)=k तथा k अचर राशि है तो

\lim _{R \rightarrow \infty} \int_{A B} f(z) d z=i(B-\alpha) K
यहां AB पर समाकलन वामावर्त दिशा में किया गया है।
(Let AB be the arc of the circle
|z|=R If \lim _{z \rightarrow \infty} z f(z)=k_{r}
Where k is a constant,then \lim _{R \rightarrow \infty} \int_{AB} f(z) d z=i(\beta-\alpha)K
the integration along AB taken in anticlockwise direction.)
उपपत्ति (Proof):इसका प्रमाण उपर्युक्त प्रमेय के अनुसार किया जा सकता है।
प्रमेय (Theorem):3.यदि 0 \leq \theta \leq \frac{\pi}{2} तो

\frac{2 \theta}{\pi} \leq \sin \theta \leq \theta  या  \frac{2}{\pi} \leq \frac{\sin \theta}{\theta} \leq 1
(If 0 \leq \theta \leq \frac{\pi}{2} then \frac{2 \theta}{\pi} \leq \sin \theta \leq \theta  or  \frac{2}{\pi} \leq \frac{\sin \theta}{\theta} \leq 1)
उपपत्ति (Proof): चूंकि cosx अन्तराल में हासमान फलन है इसलिए परास 0 \leq x \leq \theta में y=\cos x के रेखाचित्र का औसत कोटि भी निरन्तर हासमान है।
चूंकि औसत कोटि का मान

\frac{1}{\theta} \int_{0}^{\theta} \cos x d x=\frac{\sin \theta}{\theta}
है, इसलिए \theta=0 पर औसत कोटि cos0=1  के बराबर है।
अतः \theta=\frac{\pi}{2} तो औसत कोटि \frac{\sin \pi / 2}{\pi / 2}=\frac{2}{\pi} के बराबर है।
अतः जब \theta \leq \theta \leq \frac{\pi}{2} तो 1 \geq \frac{\sin \theta}{\theta} \geq \frac{2}{\pi}
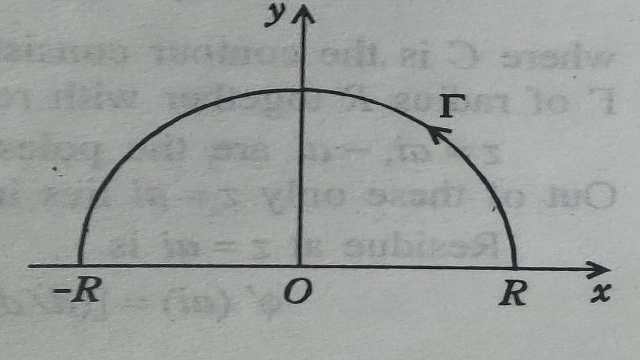
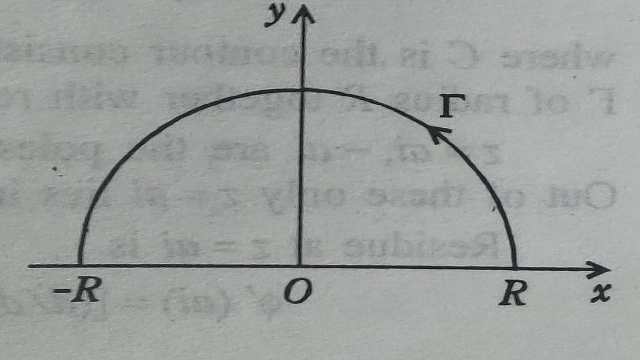
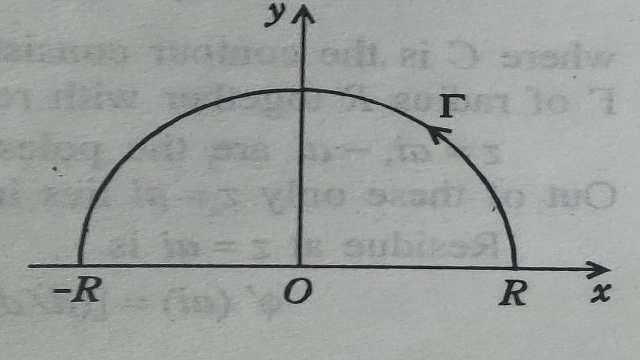
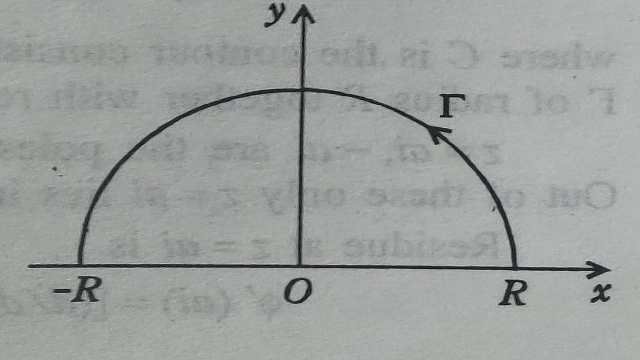
प्रमेय:4(जोरदां ).मान लें m>0 तथा \gamma अर्धवृत्त |z|=R है तथा फलन f(z) निम्न प्रतिबन्धों को सन्तुष्ट करता है:
(i)f(z) उपरि अर्धतल में अनन्तकी फलन है:
(ii)जब |z| \rightarrow \infty तो 0 \leq \arg z \leq \pi के लिए f(z) एकसमानत: 0 की ओर अग्रसर होता है।तो \lim _{R \rightarrow \infty} \int e^{i m x} f(z) d z=0
(Let m>0 and be a semicircle with centre at the origin and radius R ,and let f(z) satisfies the Conditions:
(i)f(z) is meromorphic in the upper half plane.
(ii)uniformly as |z| \rightarrow \infty for 0 \leq \arg z \leq \pi then

\lim _{R \rightarrow \infty} \int e^{i m z} f(z) d z=0
उपपत्ति (Proof):हम R को इतना वृहत् लेते हैं कि f(z) की सभी विचित्रताएं अर्द्धवृत्त के अन्दर रहे तथा कोई भी परिधि पर नहीं रहे।
चूंकि \lim _{R \rightarrow \infty} f(z)=0 इसलिए |z|=R पर पर्याप्त वृहत z के लिए |f(z)|<\varepsilon अब \left|\int_{\gamma} e^{i m z} f(z) d z\right| \leq \int_{r}\left|e^{i m z}\right||f(z)||d z| \\ \leq \varepsilon \int_{0}^{\pi}\left|e^{i m z}\right| |d z| \quad[ \because |f(z)|<\varepsilon] \\ \leq \varepsilon \int_{0}^{\pi}\left|e^{i m(R \cos \theta+i R \sin \theta)}\right| \mid R e^{i \theta \cdot i d \theta]} \\\left[\because z=R e^{i \theta}\right] \\ \leq \varepsilon \int_{0}^{T}\left|e^{i m R \cos \theta} \cdot e^{-m R \sin \theta}\right| R d \theta\\ \leq \varepsilon \int_{0}^{\pi} e^{-m R \cdot \sin \theta} \cdot R d \theta=2 \sum R \int_{0}^{\pi / 2} e^{-m R \sin \theta} d \theta \\ \left[| e^{i m R \cos \theta}\mid=1\right] \\ \leq 2 \sum R \int_{0}^{\pi / 2} e^{ \frac{-2m R \theta}{\pi}} d\theta (जोरदां असमिका द्वारा) 

\leq \frac{\pi \varepsilon}{\pi}\left(1-\bar{e}^{m R}\right)
अतः \int_{r} e^{i m z} f(z) d z \mid<\frac{\pi }{m} \sum \left(1-e^{-m R}\right)
जब R \rightarrow \infty तथा \varepsilon \rightarrow \infty हो तो असमिका का दक्षिण पक्ष शून्य को अग्रसर होता है।
परिणामत: \lim _{R \rightarrow \infty} \int_{\gamma} e^{i m z} f(z) d z=0
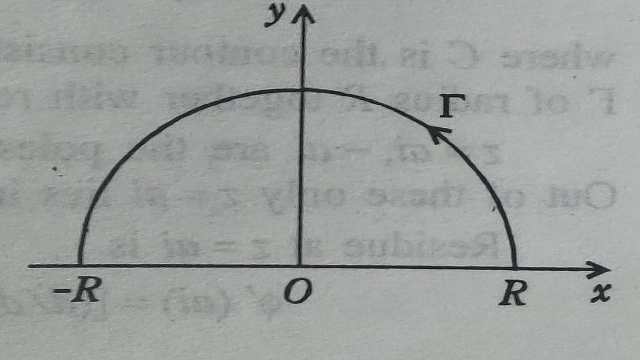
प्रमेय(Theorem):5.यदि फलन f(z) निम्न प्रतिबन्धों को सन्तुष्ट करता है
(i)f(z) उपरि z-अर्धतल में अनन्तकी फलन है,
(ii)वास्तविक अक्ष पर f(z) के अनन्तक नहीं है,
(iii) 0 \leq \arg z \leq \pi के लिए zf(z) \rightarrow 0 एकसमानत: यथा
(iv) \int_{0}^{\infty} f(x) d x तथा \int_{-\infty}^{\infty} f(x) d x दोनों अभिसारी हैं,
तो \int_{-\infty}^{\infty} f(x) d x=2 \pi i \varepsilon R^{+} यहां पर फलन के उपरि z-अर्धतल में स्थित अनन्तकों पर अवशेषों का योग है।
(Let f(z) be a function of complex variable z satisfying the following conditions.
(i)f(z) is meromorphic in the upper half of the z-plane.
(ii)f(z) has no poles on the real axis,
(iii) uniformly,as zf(z) \rightarrow 0, for 0 \leq \arg z \leq \pi
(iv)both \int_{0}^{\infty} f(x) d x and \int_{-\infty}^{\infty} f(x) d x  converge.
then \int_{-\infty}^{\infty} f(x) d x=2 \pi i \varepsilon R^{+}, where denotes the sum of the residues of f(z) at its poles in the upper half of z-plane.)
उपपत्ति (Proof):मान लें कि परिरेखा C के भाग (i) वास्तविक अक्ष पर -R व R के मध्य अन्त;खण्ड (ii)उपरि अर्धतल में अर्धवृत्त \gamma :|z|=R है। यहां पर R इतना वृहत् लिया गया है कि f(z) के सभी अनन्तक C के अन्दर स्थित है।अब समाकल \int_{C} f(z) d z को लीजिए।

\int_{C} f(z) d z=\int_{-R}^{R} f(x) d x+\int_{\gamma } f(z) d z-2 \pi i \varepsilon R^{+}...(1)
किसी भी धन \varepsilon \rightarrow 0 के लिए, परिकल्पना (iii) के अनुसार पर्याप्त वृहत् R लेने पर,वृत्त \gamma पर प्रत्येक z के लिए |zf(z)|<\varepsilon
अतः इस प्रकार के R के लिए 

\int_{\gamma}^{\pi} f(z) \cdot d z\left|=\int_{0}^{\pi} f\left(R e^{i \theta}\right) \cdot R e^{i \theta} i d \theta\right| \leq \varepsilon \pi \rightarrow 0
यथा R \rightarrow \infty, \varepsilon \rightarrow 0
अब परिकल्पना (iv) के अनुसार

\int_{-\infty}^{\infty} f(x) d x=\lim_{R \rightarrow \infty} \int_{R}^{R} f(x) d x
समीकरण (1) के दोनों पक्षों में सीमा R \rightarrow \infty लेने पर-

\int_{-\infty}^{\infty} f(x) d x=2 \pi i \varepsilon R^{+}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Residue in Complex Analysis

2.सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने के उदाहरण (Solve Complex Contour Integration Examples),कन्टूर समाकलन हल सहित उदाहरण (Contour Integration Solved Examples),परिरेखा समाकलन के उदाहरण (Contour Integration Examples),कन्टूर समाकलन अवशेष प्रमेय के उदाहरण (Contour Integration Residue Theorem Examples)-

सिद्ध कीजिए (Prove that):
Example-1.\int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta}=\frac{2 \pi}{\sqrt{\left(a^{2}-b^{2}\right)}},(a>b>0)
Solution–\int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta}=\frac{2 \pi}{\sqrt{\left(a^{2}-b^{2}\right)}}
माना कि I=\int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta}
इस समाकलन की कन्टूर (परिरेखा) इकाई त्रिज्या का वृत्त है क्योंकि \thetaकी सीमा 0 से 2 \pi है।
समाकलन में z=e^{i \theta}, d \theta=\frac{d z}{i z} प्रतिस्थापन करने पर-

I=\frac{1}{i} \int_{c} \frac{d z}{\left[a+\frac{b}{2}\left(z+\frac{1}{2}\right)\right] z}
[यहां पर C इकाई त्रिज्या वाला वृत्त C:|Z|=1 है]

=\frac{1}{i} \int_{c} \frac{2 d z}{2 a z+b z^{2}+b} \\ =\frac{1}{b i} \int_{c} \frac{2 d z}{\left(z^{2}+\frac{2 a z}{b}+1\right)} \\ =\frac{2}{b i} \int_{c} \frac{d z}{\left[z-\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right)\right] \left[z+ \left(\frac{a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]} =\int_{c} g(z) d z \\ g(z)=\frac{2}{b i} \frac{1}{\left[z-\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]\left[z+\left(\frac{a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]}
स्पष्टत: g(z) के अनन्तक हैं।ये अनन्तक समीकरण (z^{2}+\frac{2 a z}{b}+1) के मूल हैं।
माना z=\frac{-a+\sqrt{a^{2}-b^{2}}}{b}=\alpha
तथा z=\frac{-a-\sqrt{a^{2}-b^{2}}}{b}=\beta
तो z=\alpha तथा z=\beta सरल अनन्तक है एवं \alpha \beta =1
चूंकि |\alpha|=\left|\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right|<1
इसलिए |\beta|=\left|\frac{-a-\sqrt{a^{2}-b^{2}}}{b}\right|>1
अतः एक ही अनन्तक z=\alpha,C के अन्दर स्थित है।
z=\alpha पर g(z) का अवशेष=\lim _{z \rightarrow \alpha}(z-\alpha) g(z) \\ =\lim _{z \rightarrow \alpha} \left(\frac{\theta}{b i}\right)(z-\alpha) \cdot \frac{1}{(z-\alpha)(z-\beta)} \\ =\frac{2}{b i} \cdot \frac{1}{(\alpha-\beta)} \\ =\frac{2}{b i} \cdot \frac{1}{\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}+\frac{a+\sqrt{a^{2}-b^{2}}}{b}\right)} \\ =\frac{2}{b i} \cdot \frac{b}{2 \sqrt{a^{2}-b^{2}}} \\ =-\frac{i}{\sqrt{a^{2}-b^{2}}}=\sum R^{+}
अब कोशी अवशेष के अनुप्रयोग से

\int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta} =2 \pi i \sum R^{+} \\ =2 \pi i\left(\frac{-i}{ \sqrt{a^{2}-b^{2}}}\right) \\ \int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta} =\frac{2 \pi}{\sqrt{a^{2}-b^{2}}}

उपर्युक्त उदाहरण के द्वारा सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को समझ सकते हैं।
Example-2.\int_{0}^{2 \pi} \frac{\sin ^{2} \theta d \theta}{a+b \cos \theta}=\frac{2 \pi}{b^{2}}\left[a-\sqrt{\left(a^{2}-b^{2}\right)}\right] ;(a>b>0)
Solution–\int_{0}^{2 \pi} \frac{\sin ^{2} \theta d \theta}{a+b \cos \theta}=\frac{2 \pi}{b^{2}}\left[a-\sqrt{\left(a^{2}-b^{2}\right)}\right]
माना कि I=\int_{0}^{2 \pi} \frac{\sin ^{2} \theta d \theta}{a+b \cos \theta}
इस समाकलन की कन्टूर (परिरेखा) इकाई त्रिज्या का वृत्त है क्योंकि \theta की सीमा 0 से 2 \pi है।
समाकलन में z=e^{i \theta} ; d \theta=\frac{d z}{i z} प्रतिस्थापन करने पर-

I=-\frac{1}{4 i} \int_{c} \frac{\left(z-\frac{1}{2}\right)^{2} d z}{\left[a+\frac{b}{2}\left(z+\frac{1}{z}\right)\right] z} \\ =-\frac{1}{4 i} \int_{c} \frac{\left(z^{2}-1\right)^{2} d z}{z^{2}\left[a z+\frac{b z^{2}}{2}+\frac{b}{2}\right]} \\ =-\frac{1}{4 i b} \int_{c} \frac{2\left(z^{2}-1\right)^{2} d z}{z^{2}\left( z^{2}+\frac{2 a z}{b}+1\right)}
[यहां पर C इकाई त्रिज्या वाला वृत्त c:|z|=1 है]

=-\frac{1}{2 i b} \int_{c} \frac{ {\left(z^{2}-1\right)^{2}}d z}{z^{2}\left[z-\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]\left[z +\left(\frac{a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]} \\ g(z)=-\frac{1}{2 i b} \frac{\left(z^{2}- 1\right)^{2}}{z^{2}\left[z-\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]\left[z+(\frac{a+\sqrt{a^{2}-b^{2}}}{b})\right]}
अब g(z) का z=0 पर कोटि-2 का अनन्तक हैं, z=\alpha एवं z=\beta पर सरल अनन्तक हैं जबकि \alpha व \beta,(z^{2}+\frac{2 a}{b} z+1)=0 के मूल हैं अर्थात्
\alpha=\frac{-a+\sqrt{a^{2}-b^{2}}}{b}  तथा \beta=\frac{-a-\sqrt{a^{2}-b^{2}}}{b}
चूंकि a>b>0 , इसलिए |\beta|>a / b>1 लेकिन |\alpha \beta|=1 अतः

|\alpha |<1
इस प्रकार सरल अनन्तक z=\alpha वृत्त के अन्दर स्थित है तथा सरल अनन्तक z=\beta वृत्त के बाहर स्थित है।
अब g(z) का z=\alpha पर अवशेष

R_{1} =\lim _{z \rightarrow \alpha}(z-\alpha) g(z) \\ =\lim _{z \rightarrow \alpha}(z-\alpha) \cdot \frac{\left.z^{2} -1\right)^{2}}{(-2 i b) z^{2}(z-\alpha)(z+\beta)} \\ =\frac{\left(\alpha^{2}-\alpha \beta\right)^{2}}{\alpha^{2}(-2 i b)(\alpha-\beta)} \\ =\frac{(\alpha-\beta)^{2}}{(-2 i b)(\alpha-\beta)} \\ =\frac{\alpha-\beta}{-2 i b} \\ =\frac{\left(-\frac{a+\sqrt{{a}^{2}-b^{2}}}{b}+\frac{a+\sqrt{a^{2}-b^{2}}}{b}\right)}{-2 i b} \\ =\frac{2 \sqrt{a^{2}-b^{2}}}{-2 i b^{2}} \\ \Rightarrow R_{1} =\frac{\sqrt{a^{2}-b^{2}}}{-i b^{2}}=\frac{i \sqrt{a^{2}-b^{2}}}{b^{2}}
g(z) का z=0 पर अवशेष ज्ञात करने के लिए हम \frac{\left(z^{2}-1\right)^{2}}{z^{2}(-2 i b)(z-\alpha)(z-\beta)} का घात श्रेणी प्रसार करते हैं।
यह प्रसार है-

=-\frac{1}{2 i b z^{2}}\left(1-2 z^{2}+z^{4}\right)\left(1+\frac{2 a}{b} z+z^{2}\right)^{-1} \\ =\frac{1}{2 i b z^{2}}\left(1-2 z^{2}+z^{4}\right)\left[x-2\left(\frac{a}{b}\right) z+z^{2}+\left(\frac{2 a}{b} z+z^{2}\right)^{2}\right]
अब g(z) के घात श्रेणी प्रसार में का गुणांक उपर्युक्त घात श्रेणी प्रसार में z के \frac{1}{z} गुणांक के बराबर है। अतः g(z) का अनन्तक z=0 पर अवशेष

R_{2} =-\frac{1}{2 i b}\left(-\frac{2 a}{b}\right) \\ =\frac{a}{i b^{2}} \\ \Rightarrow R_{2} =\frac{-a i}{b^{2}} \\ \sum R^{+}=R_{1}+R_{2} =\frac{i \sqrt{a^{2}-b^{2}}}{b^{2}}-\frac{a i}{b^{2}}
अब कोशी अवशेष के अनुप्रयोग से

\int_{0}^{2 \pi} \frac{\sin ^{2} \theta d \theta}{a+b \cos \theta} =2 \pi i \sum R^{+} \\ =2 \pi i\left(\frac{i \sqrt{a^{2}-b^{2}}}{b^{2}}-\frac{a i}{b^{2}}\right) \\ \Rightarrow \int_{0}^{2 \pi} \frac{\sin ^{2} \theta d \theta}{a+b \cos \theta} =\frac{2 \pi}{b^{2}}\left(a-\sqrt{a^{2}-b^{2}}\right)

उपर्युक्त उदाहरण के द्वारा सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को समझ सकते हैं।
Example-3.\int_{0}^{2 \pi} \frac{d \theta}{(a+b \cos \theta)^{2}}=\frac{2 \pi a}{\left(a^{2}-b^{2}\right)^{3 / 2}},(a>b>0)
Solution–\int_{0}^{2 \pi} \frac{d \theta}{(a+b \cos \theta)^{2}}=\frac{2 \pi a}{\left(a^{2}-b^{2}\right)^{3 / 2}}
माना कि I=\int_{0}^{2 \pi} \frac{d \theta}{(a+b\cos \theta)^{2}}
इस समाकलन की कन्टूर (परिरेखा) इकाई त्रिज्या का वृत्त है क्योंकि \theta की सीमा 0 से 2 \pi है।
समाकलन में z=e^{i \theta}, d \theta=\frac{d z}{i z} प्रतिस्थापन करने पर-

I =\frac{1}{i} \int_{c} \frac{d z}{\left[a+\frac{b}{2}\left(z+\frac{1}{2}\right)\right]^{2} z} \\ =\frac{1}{i} \int_{c} \frac{4 z d z}{\left(2 a z+b z^{2}+b\right)^{2}} \\ =\frac{4}{i} \int_{c} \frac{2 d z}{b^{2}\left(z^{2}+\frac{2 a}{b} z+1\right)^{2}} \\ =\frac{4}{i b^{2}} \int_{c} \frac{z d z}{\left(z^{2}+\frac{z a z}{b}+1\right)^{2}}
[यहां पर C इकाई त्रिज्या वाला C:|z|=1 वृत्त है]

I=\frac{4}{i b^{2}} \int_{c} \frac{z d z}{\left[z-\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]^{2}\left[z +\frac{\left(a+ \sqrt{a^{2}+b^{2}}\right)}{b}\right]^{2}}=\int_{c} g(z) d z \\ g(z)=\frac{4}{i b^{2}} \frac{z}{\left[z-\left(\frac{-a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]^{2}\left[z+\left(\frac{a+\sqrt{a^{2}-b^{2}}}{b}\right)\right]^{2}}
अब: g(z) का z=\alpha तथा z=\beta कोटि-2 का अनन्तक हैं।जबकि \alpha व \beta , \left(z^{2}+\frac{2a}{b} z+1\right)=0 के मूल हैं।
जहां \alpha=\frac{-a+\sqrt{a^{2}-b^{2}}}{b}, \beta=\frac{-a-\sqrt{a^{2}-b^{2}}}{b}
चूंकि aa>b>0 इसलिए लेकिन
इस प्रकार द्विकोटि का अनन्तक z=\alpha वृत्त के अन्दर स्थित है तथा द्विकोटि का अनन्तक z=\beta वृत्त C के बाहर स्थित है।
अब g(z) का z=\alpha पर अवशेष
g(z)=\frac{4}{i b^{2}} \cdot \frac{1}{(z-\alpha)^{2}} \phi(z) (माना)

\phi^{\prime}(\alpha)=\left[\phi^{\prime}(z)\right]_{z=\alpha} \\ =\frac{4}{i b^{2}}\left[\frac{(z-\beta)^{2}-2 z(z-\beta)}{(z-\beta)^{4}} \right]_{z=\alpha} \\ =\frac{4}{i b^{2}}\left[\frac{(\alpha-\beta)^{2}-2 \alpha(\alpha-\beta)}{(\alpha-\beta)^{4}}\right] \\ =\frac{-4 i}{b^{2}} \cdot \frac{-(\alpha+\beta)}{(\alpha-\beta)^{3}} \\ =\frac{4 i}{b^{2}} \frac{\left(-\frac{a+\sqrt{a^{2}-b^{2}}}{b}+\frac{a-\sqrt{a^{2}-b^{2}}}{b}\right)}{\left(-\frac{a +\sqrt{a^{2}-b^{2}}}{b}+\frac{a+ \sqrt{a^{2}-b^{2}}}{b}\right)^{3}} \\ =\frac{4 i}{b^{2}} \frac{\left(-\frac{2 a}{b}\right)}{\left(2 \sqrt{a^{2}-b^{2}}\right)^{3}} \\ =\frac{-a i}{\left(a^{2}-b^{2}\right)^{3 / 2}}=\sum R^{+}
अब कोशी अवशेष के अनुप्रयोग से

\int_{0}^{2 \pi} \frac{d \theta}{\left(a+b\cos \theta)^{2}\right.} =2 \pi i \sum R^{+} \\ =2 \pi i\left(\frac{-a i}{\left(a^{2}-b^{2}\right)^{3 / 2}}\right) \\ \Rightarrow \int_{0}^{2 \pi} \frac{d \theta}{(a+b \cos \theta)^{2}} =\frac{2 \pi a}{\left(a^{2}-b^{2}\right)^{3 / 2}}
Example-4. \int_{0}^{\pi} \frac{\cos 2 \theta d \theta}{1-2 a \cos \theta+a^{2}}=\frac{\pi a^{2}}{1-a^{2}},(-1<a<1)
Solution– \int_{0}^{\pi} \frac{\cos 2 \theta d \theta}{1-2 a \cos \theta+a^{2}}=\frac{\pi a^{2}}{1-a^{2}}
माना कि I=\int_{0}^{\pi} \frac{\cos 2 \theta d \theta}{1-2 a \cos \theta+a^{2}} \\ = \frac{1}{2} \int_{0}^{2 \pi} \frac{\cos 2 \theta d \theta}{1-2 a \cos \theta+a^{2}} \\ =\frac{1}{2} \text{Real part of} \int \frac{e^{i 2 \theta}}{1-2 a \cos \theta+a^{2}} d \theta
Put z=e^{i \theta} \Rightarrow d \theta=\frac{d z}{i z} \\ =\frac{1}{2} \text{Real part of} \int \frac{z^{2}}{1-a\left(z+\frac{1}{z}\right)+a^{2}} \cdot \frac{d z}{i z} \\ =\frac{1}{2} \text{Real part of} \int_{c} \frac{z^{2}}{c(1-a z)(z-a)} d z \\ =\frac{1}{2} \text{Real part of} \int f(z) d z
C इकाई त्रिज्या का वृत्त है।
(1-a z)(z-a)=0 \Rightarrow z=a,\frac{1}{a} जो कि f(z) के सरल अनन्तक हैं।z=a सरल अनन्तक है जो वृत्त के अन्दर स्थित है।
अतः z=a पर अवशेष=\lim _{z \rightarrow a}(z-a) f(z) \\ =\lim _{z \rightarrow a}(z-a) z^{2} \\ =\lim _{z \rightarrow a} \frac{z^{2}}{i(1-a z)} \\ =\frac{a^{2}}{i\left(1-a^{2}\right)}=\sum R^{+}
अब कोशी अवशेष के अनुप्रयोग से

\int_{c} f(z) d z =2 \pi i \sum R^{+} \\ =2 \pi i \cdot \frac{a^{2}}{\hat{i}\left(1-a^{2}\right)} \\ =\frac{2 \pi a^{2}}{\left(1-a^{2}\right)}
अतः \int_{0}^{\pi} \frac{\cos 2 \theta}{1-2 a \cos \theta+a^{2}} d \theta=\frac{1}{2} \text{Real part of} \int_{c} f(z) d z \\ \Rightarrow \int_{0}^{\pi} \frac{\cos 2 \theta}{1-2 a \cos \theta+a^{2}}=\frac{\pi a^{2}}{\left(1-a^{2}\right)}
Example-5. \int_{0}^{\infty} \frac{d x}{1+x^{2}}=\frac{\pi}{2}
Solution–\int_{0}^{\infty} \frac{d x}{1+x^{2}}=\frac{\pi}{2}
माना \int_{c} f(z) d z=\int_{c} \frac{d z}{1+z^{2}} जहां C कन्टूर है।

कोशी अवशेष प्रमेय से-

\int_{C} f(z) d z=\int_{-R}^{R} \frac{d x}{1+x^{2}}+\int_{F} \frac{d z}{1+z^{2}}=2 \pi i \sum R^{+}.....(1) \\ \lim _{R \rightarrow \infty} z f(z)=\lim _{z \rightarrow \infty} \frac{z}{1+z^{2}}=0
अतः \lim _{R \rightarrow \infty} \int \frac{d z}{1+z^{2}}=0
पुनः z=\pm i,f(z) के सरल अनन्तक हैं। इनमें से z=i वृत्त C के अन्दर स्थित है।
अतः z=i पर अवशेष=\lim _{z \rightarrow i}(z i) f(z) \\ =\lim _{z \rightarrow i} \frac{(z-i) \cdot 1}{\left(z^{2}+1\right)} \\ =\lim _{z \rightarrow i}(z-i) \frac{1}{(z+i)(z+i)} \\ =\lim _{z \rightarrow i} \frac{1}{(z+i)} \\ \sum R^{+}=\frac{1}{2 i}
समीकरण (1) में मान रखने पर-

\int_{-\infty}^{\infty} \frac{d x}{1+x^{2}}=2 \pi i \cdot \frac{1}{2 i} \\ \Rightarrow 2 \int_{0}^{\infty} \frac{d x}{1+x^{2}}=\pi \\ \Rightarrow \int_{0}^{\infty} \frac{d x}{1+x^{2}}=\pi / 2

उपर्युक्त उदाहरण के द्वारा सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को समझ सकते हैं।
Example-6.\int_{-\infty}^{\infty} \frac{x^{2} d x}{\left(x^{2}+a^{2}\right)^{3}}=\frac{\pi}{8 a^{3}},(a>0)
Solution–\int_{-\infty}^{\infty} \frac{x^{2} d x}{\left(x^{2}+a^{2}\right)^{3}}=\frac{\pi}{8 a^{3}}
माना \int_{c} f(z) d z=\int_{c} \frac{z^{2}}{\left(z^{2}+a^{2}\right)^{3}} d z
जहां C कन्टूर है।

कोशी अवशेष प्रमेय से-

\int_{C} f(z) d z=\int_{-R}^{R} \frac{x^{2}}{\left(x^{2}+a^{2}\right)^{3}} d x+\int \frac{z^{2} d z}{\left(z^{2}+a^{2}\right)^{3}}=2 \pi i \sum R^{+}.....(1)
जबकि \lim _{R \rightarrow \infty} z f(z)=\lim _{z \rightarrow \infty} z \cdot \frac{z^{2}}{\left(z^{2}+a^{2}\right)^{3}}=0
अतः \lim _{R \rightarrow \infty} \int_{-} \frac{z^{2}}{\left(z^{2}+a^{2}\right)^{3}} d z=0 \\ z^{2}+a^{2}=0 \Rightarrow z=\pm a i,f(z) कोटि-3 के अनन्तक है।
इनमें z=ai वृत्त के अन्दर स्थित है।
अतः z=ai पर अवशेष=\frac{1}{2!}\left[\frac{d^{2}}{d z^{2}} \frac{z^{2}}{(z+a i)^{3}}\right]_{z=a i} \\ = \frac{1}{2 !}\left[\frac{d}{d z} \frac{(z+a i)^{3}.2 z-z^{2} \cdot 3(z+a i)^{2}}{(z+a i)^{6}}\right]_{z=a i}\\ = \frac{1}{2}\left[\frac{d}{d z} \frac{2 z( z+a i)-3 z^{2}}{(z+a i)^{4}}\right]_{z=a i} \\= \frac{1}{2}\left[\frac{d}{d z} \frac{2 z^{2}+2 a z i-3 z^{2}}{(z+a i)^{4}}\right]_{z=a i} \\  =\frac{1}{2}\left[\frac{d}{d z} \frac{2 a z i-z^{2}}{(z+a i)^{4}}\right]_{z=a i} \\ =\frac{1}{2}\left[\frac{(z+a i)^{4}(2 a i-2 z)-\left(2 a z i-z^{2}\right) \cdot 4(z+a i)^{3}}{(z+a i)^{8}}\right]_{z=a i}\\ = \frac{1}{2}\left[\frac{(z+a i)(2 a i-2 z)-4\left(2 a z i-z^{2}\right)}{(z+a i)^{5}}\right]_{z=a i} \\ =\frac{1}{2}\left[\frac{2 a i z-2 z^{2}+2 a^{2}-2 a i z-8 a z i+4 z^{2}}{(z+a i)^{5}}\right]_{z=a i} \\ =\frac{1}{2}\left[\frac{-2 a^{2}+2 z^{2}-8 a z i}{(z+a i)^{5}}\right]_{z=a i} \\=\frac{1}{2}\left[\frac{-4 a^{2}+8 a^{2}}{(2 a i)^{5}}\right] \\ =\frac{2 a^{2}}{32 a^{5} i} \\ \sum R^{+} =\frac{a^{2}}{16 a^{5} i}=\frac{1}{16 a^{3} i}
समीकरण (1) से-

\int_{-\infty}^{\infty} \frac{z^{2}}{\left(z^{2}+a^{2}\right)^{3}} d z =2 \pi i \sum R^{+} \\ =2 \pi i\left(\frac{1}{16 a^{3} i}\right) \\ \Rightarrow \int_{-\infty}^{\infty} \frac{z^{2}}{\left(z^{2}+a^{2}\right)^{3}} =\frac{\pi}{8 a^{3}}

उपर्युक्त उदाहरण के द्वारा सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को समझ सकते हैं।
Example-7.\int_{-\infty}^{\infty} \frac{x^{2} d x}{\left(x^{2}+1\right)^{2} \cdot\left(x^{2}+2 x+2\right)}=\frac{7 \pi}{50}
Solution–\int_{-\infty}^{\infty} \frac{x^{2} d x}{\left(x^{2}+1\right)^{2} \cdot\left(x^{2}+2 x+2\right)}=\frac{7 \pi}{50}
माना \int_{c} f(z)=\int \frac{z^{2} d z}{\left(z^{2}+1\right)^{2}\left(z^{2}+2 z+2\right)}
जहां C कन्टूर है।

कोशी अवशेष प्रमेय से-

\int_{c} f(z) d z=\int_{\gamma} \frac{z^{2} d z}{\left(z^{2}+1\right)^{2}\left(z^{2}+2 z+2\right)}+\int_{-R}^{R}\frac{x^{2} d z}{\left(x^{2}+1\right)^{2}\left(x^{2}+2x+2\right)}=2 \pi i \sum R^{+}.....(1)
जबकि \lim _{R \rightarrow \infty} zf(z)=\lim _{z \rightarrow \infty} z \cdot \frac{z^{2} d z}{\left(z^{2}+ 1\right)^{2}\left(z^{2}+2 z+2\right)}=0
अतः \lim _{z \rightarrow \infty} \int \frac{z^{2} d z}{\left(z^{2}+1\right)^{2}\left(z^{2}+2 z+2\right)} =0 \\ z^{2}+1=0 \Rightarrow z=\pm i, z^{2}+2 z+2=0 \\  \Rightarrow z =\frac{-2 \pm \sqrt{(2)^{2}-8}}{2} \\ z =\frac{-2 \pm 2 i}{2} \\ \Rightarrow z =-1 \pm i
अतः f(z) के अनन्तक है z=\pm i, z=-1 \pm i
z=\pm i कोटि-2 तथा z=-1 \pm i साधारण अनन्तक हैं।
इनमें से z=i ,z=-1+i ,C के अन्दर स्थित है।
z=i पर अवशेष=\lim _{z \rightarrow i} \frac{d}{d z} (z-i)^{2} \frac{z^{2}}{(z+i)^{2}(z-i)^{2}\left(z^{2}+2 z+2\right)} \\ =\lim _{z \rightarrow i} \frac{d}{d z} \frac{z^{2}}{d x i^{2}\left(z^{2}+2 z+z\right)} \\ =\lim _{z \rightarrow i} \frac {(z+i)^{2} \left(z^{2}+2 z+2\right) \cdot 2^{2}-z^{2}\left[2(z+c)\left(z^{2}+2 z+2\right)+(z+i)^{2}(2 z+2)\right]}{(z+i)^{4} \left(z^{2}+2 z+2\right)^{2}} \\ =\lim _{z \rightarrow i} \frac{2 z(z+i)\left(z^{2}+2 z+2\right)-z^{2}\left[2 z^{2}+4 z+4+(z+i)(2 z+2)\right]}{(z+i)^{3}\left(z^{2}+2 z+2\right)^{2}} \\ =\lim _{z \rightarrow i} \frac{\left(2 z^{2}+2 z i\right) \left(z^{2} +2 z+2\right)-z^{2}\left[2 z^{2}+4 z+4+2 z^{2}+2 z+2 z i+2 i\right]}{(z+i)^{3}\left(z^{2}+2 z+2\right)^{2}} \\ =\lim _{z \rightarrow i} \frac{\left(2 i^{2}+2 i^{2}\right)\left(i^{2}+2 i+2\right)-i^{2}\left(4 i^{2}+6 i-2+4+2 i\right)}{(i+i)^{3}\left(i^{2}+2 i+2\right)^{2}} \\ =\lim _{z \rightarrow i} \frac{\left(4 i^{2}\right)(2 i+1)+(-4+8 i+2)}{(2 i)^{3}(2 i+1)^{2}} \\ =\lim _{z \rightarrow i} \frac{-4(2 i+1)+(8 i-2)}{(-8 i)(2 i+1)^{2}} \\ =\lim _{z \rightarrow i} \frac{-8 i-4+8 i-2}{(-8 i)(2 i+1)^{2}} \\ =\lim _{z \rightarrow i} \frac{-6}{(-8 i)(2 i+1)^{2}} \\ =\lim _{z \rightarrow i} \frac{-6}{(-8 i)(-4+1+4i)} \\ =\lim _{z \rightarrow i} \frac{3}{4 i(4 i-3)} \\ =\lim _{z \rightarrow i} \frac{3}{4 (4 i^{2}-3i)} \\ =\lim _{z \rightarrow i} \frac{3}{-4 (3 i+4)}

z=-1+i पर अवशेष=\lim _{z \rightarrow(-1+i)} \frac{(z+1-i) z^{2}}{(z+i)^{2}(z-i)^{2}(z+1-i)(z+1+i)} \\ =\lim _{z \rightarrow(-1+i)} \frac{z^{2}}{(z+i)^{2}(z-i)^{2}(z+1+i)} \\ =\frac{(-1+i)^{2}}{(-1+i+i)^{2}(-1+i-i)^{2}(-1+i+1+i)} \\ =\frac{(-1+i)^{2}}{(-1+i+i)^{2}(-1+i-i)^{2}(-1+i+1+i)} \\ =\frac{1-1-2 i}{(2 i-1)^{2}(-1)^{2}(2 i)} \\ =\frac{-2 i}{2 i\left(4 i^{2}+1-4 i\right)} \\ =\frac{-1}{(-4 i-3)} \\ =\frac{1}{(4 i+3)}
अतः \sum R^{+} =-\frac{3}{4(3 i+4)}+\frac{1}{4 i+3} \\ =\frac{-3(4 i+3)+4(3 i+4)}{4\left(12 i^{2}+9 i+16 i+12\right)} \\ =\frac{-12 i-9+12 i+16}{4(25 i)} \\ \sum R^{+}=\frac{7}{100 i}
समीकरण (1) से-

=\sum_{\infty}^{\infty} \frac{x^{2} d x}{\left(x^{2}+1\right)^{2}\left(x^{2}+2 x+2\right)}=2 \pi i \sum R^{+} \\ =2 \pi i\left(\frac{7}{100 i}\right) \\ \Rightarrow \sum_{-\infty}^{\infty} \frac{x^{2} d x}{\left(x^{2}+ 1\right)^{2} \left(x^{2}+2 x+2\right)}=\frac{7 \pi}{50}

उपर्युक्त उदाहरण के द्वारा सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को समझ सकते हैं।
Example-8.\int_{0}^{\infty} \frac{x^{3} \sin x}{\left(x^{2}+a^{2}\right)\left(x^{2}+b^{2}\right)}=\frac{\pi}{2\left(a^{2}-b^{2}\right)} \cdot\left(a^{2} e^{-a}-b^{2} e^{-b}\right)
Solution–\int_{c} f(z)=\int \frac{x^{3} e^{i z}}{\left(z^{2}+a^{2}\right)\left(z^{2}+b^{2}\right)}

अवशेष प्रमेय से-

\int_{c} f(z) d z=\int_{-R}^{R} f(x) d x+\int_{\gamma} f(z) d z=2 \pi i \sum R^{+}
जोरदां प्रमेय से- \lim _{R \rightarrow \infty} \int_{c} f(z) d z=0 \\ \lim _{R \rightarrow \infty} \int_{-R}^{R} f(x) d x=2 \pi i \sum R^{+} \Rightarrow \int_{-\infty}^{\infty} f(x) d x=2 \pi i \sum R^{+}.....(1) \\ z^{2}+a^{2}=0 \Rightarrow z=\pm ai, z^{2}+b^{2}=0 \Rightarrow z=\pm bi
अतः साधारण अनन्तक हैं।,C के अन्दर स्थित है।
z=ai पर अवशेष R_{1}=\lim_{z \rightarrow i a}(z-i a) f(z) \\=\lim _{z \rightarrow i a} \frac{ (z-i a) z^{3} e^{i z} }{(z+i a)(z+i b)(z-i b)} \\ =\lim _{z \rightarrow i a} \frac{z^{3} e^{i z} }{(z+i a)(z+i b)(z-i b)} \\ =\frac{(i a)^{3} e^{i(i a)}}{(i a+i a)(i a+i b)(i a-(b)} \\ \Rightarrow R_{1} =\frac{-i a^{3}-a}{-2 i a\left(b^{2}-a^{2}\right)}=-\frac{a^{2} e^{-a}}{2 \cdot\left(b^{2}-a^{2}\right)}
z=ib पर अवशेष R_{2}= \lim _{z \rightarrow i b}(z-i b) f(z) \\ = \lim _{z \rightarrow i b} \frac{(z-c b) \cdot z^{3} e^{i z}}{\left(z^{2}+a^{2}\right)(z+i b)(z-i b)} \\ = \lim _{z \rightarrow i b} \frac{z^{3} e^{i z}}{\left(a^{2}+a^{2}\right)(z+i b)} \\ = \frac{(i b)^{3} e^{i(i b)}}{\left((i b)^{2}+ a^{2}\right) i b} \\ =-\frac{i b^{3} e^{-b}}{\left(a^{2}-b^{2}\right) 2 b} \\ \Rightarrow R_{2}=-\frac{b^{2} e^{-b}}{2\left(a^{2}-b^{2}\right)} \\ \sum R^{+}=R_{1}+R_{2}=-\frac{a^{2} e^{-a}}{2 \left(b^{2}-a^{2}\right)}-\frac{b^{2} e^{-b}}{2\left(a^{2}-b^{2}\right)} \\ =\frac{a^{2} e^{-a}}{2 \left(a^{2}-b^{2}\right)}-\frac{b^{2} e^{-b}}{2\left(a^{2}-b^{2}\right)} \\ \Rightarrow \sum R^{+}=\frac{1}{2\left(a^{2}-b^{2}\right)} \left(a^{2} e^{-a}-b^{2} e^{-b}\right)
(1) से-\int_{-\infty}^{\infty} \frac{x^{3} e^{i n}}{\left(x^{2}+a^{2}\right)\left(x^{2}+b^{2}\right)} d x =2 \pi c \sum R^{+} \\=2 \pi i \cdot \frac{1}{2\left(a^{2}-b^{2}\right)}\left(a^{2} e^{-a}-b^{2} e^{-b}\right) \\ \Rightarrow \int_{\infty}^{\infty} \frac{x^{3}\left(\cos x+i \sin x\right)}{\left(x^{2} +a^{2}\right)\left(x^{2}+b^{2}\right)} d x =\frac{\pi i}{a^{2}-b^{2}}\left(a^{2} e^{-a}-b^{2} e^{-b}\right)
काल्पनिक व वास्तविक भागों की तुलना करने पर-

\int_{-\infty}^{\infty} \frac{x^{3} \sin x}{\left(x^{2}+a^{2}\right)\left(x^{2}+b^{2}\right)} d x=\frac{\pi}{\left(a^{2}-b^{2}\right)}\left(a^{2} e^{-a}-b^{2} e^{-b}\right) \\ \Rightarrow \int_{0}^{0} \frac{x^{3} \sin x}{\left(x^{2}+ a^{2}\right)\left(x^{2}+b^{2}\right)} d x=\frac{\pi}{2\left(a^{2}-b^{2}\right)}\left(a^{2} e^{-a}-b^{2} e^{-b}\right)
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को समझ सकते हैं।

3.सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने की समस्याएं (Solve Complex Contour Integration Problems)-

परिरेखा समाकलन द्वारा सिद्ध कीजिए कि
(Use the method of countour integration to prove that):

(1).) \int_{0}^{2 \pi} \frac{d \theta}{1+a^{2}-2 a \cos \theta}=\frac{2 \pi}{1-a^{2}}, 0<a<1 \\ (2.) \int_{0}^{\pi} \frac{a d \theta}{a^{2}+\cos ^{2} \theta}=\frac{\pi}{\left.\sqrt{\left(1+a^{2}\right.}\right)}, a>0 \\ (3.) \int_{0}^{\pi} \frac{\sin^{4} \theta d \theta}{a+b \cos \theta}=\frac{\pi}{b^{4}}\left(a^{2}-b^{2}\right)^\frac{3}{2}-a^{3}+\frac{3}{2} a b^{2} a>b>0 \\ (4.) \int_{0}^{2 \pi} \frac{\cos 2 \theta}{5+4 \cos \theta} d \theta=\frac{\pi}{6}

उपर्युक्त सवालों को हल करके सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को ठीक से समझ सकते हैं।

4.परिरेखा समाकल से क्या मतलब है? (What is meant by contour integral?),कन्टूर समाकल को कैसे हल करें? (How to solve contour integrals?)-

परिरेखा समाकलन सम्मिश्र समतल में दिए गए परिरेखा (कन्टूर) के आसपास परिरेखा समाकल के मूल्यों की गणना करने की प्रक्रिया है।होलोमोर्फिक फलनों की वास्तव में आश्चर्यजनक गुणधर्मों के परिणामस्वरूप, परिरेखा के अंदर सम्मिश्र अवशेषों के मूल्यों को संक्षेप में इस तरह के समाकल भाग की आसानी से गणना की जा सकती है।

5.आप सम्मिश्र परिरेखा समाकलन कैसे हल करते हैं? (How do you solve complex contour integration?)-

परिरेखा समाकलन में, परिरेखा (कन्टूर) वक्र की एक सटीक परिभाषा प्रदान करते हैं जिस पर एक समाकल उपयुक्त रूप से परिभाषित किया जा सकता है।सम्मिश्र समतल में एक वक्र के रूप में परिभाषित किया गया है।
परिरेखा समाकलन एक शक्तिशाली तकनीक है,जो सम्मिश्र विश्लेषण पर आधारित है, जो हमें कुछ ऐसे इंटीग्रल्स को हल करने की अनुमति देती है जो अन्यथा मुश्किल या हल करना असंभव है।
परिरेखा समाकलन द्वारा समाकलन ज्ञात करने की विधि ऊपर दी गई है।

6.आप समाकलन के लिए परिरेखा कैसे चुनते हैं? (How do you choose contour for integration?)-

एक साधारण परिरेखा (कन्टूर) के लिए बंद परिरेखा (कन्टूर) को एक या एक से अधिक अनन्तकों को जोड़ना होगा अन्यथा समाकल शून्य है।यदि समतल में एक या एक से अधिक “कटौती” होती है, तो स्थिति अधिक सम्मिश्र है और मामले के आधार पर मामले को संभालने की आवश्यकता है।(एक कट एक फंक्शन द्वारा उत्पन्न होता है जैसे कि वर्गमूल या लघुगणक।)

7.इंजीनियरिंग में कन्टूर समाकलन का अनुप्रयोग (Application of contour integration in engineering)-

परिरेखा समाकलन एन्ट्रापी अध्ययन में प्रकट होता है और अवशेषों के सिद्धांत की रीढ़ है जो बदले में, कुछ अनुचित इंटीग्रल्स का मूल्यांकन करने के लिए कई प्रसिद्ध अनुप्रयोगों का पता लगाता है, और फ्यूरियर, लाप्लास और जेड ट्रांसफॉर्म की गणना करने के लिए एक फोर्टियरी, उन सभी में बुनियादी उपकरण परिचालन कैलकुलस और सिग्नल विश्लेषण, सीएफ।
उपर्युक्त उदाहरणों,प्रश्नों के उत्तर तथा सवालों को हल करके सम्मिश्र परिरेखा (कन्टूर) समाकलन द्वारा हल करने (Solve Complex Contour Integration) को भली-भांति समझ सकते हैं।

Also Read This Article:-Argument Principle and Rouche Theorem

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here