Complex Contour Integration Examples
1.सम्मिश्र कन्टूर समाकलन उदाहरण का परिचय (Introduction to Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration)-
इससे पूर्व आर्टिकल्स सम्मिश्र परिरेखा समाकलन को सम्मिश्र कन्टूर समाकलन (Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration) उदाहरणों के द्वारा समझ चुके हैं।इस आर्टिकल में कुछ ओर विशिष्ट उदाहरणों के द्वारा परिरेखा समाकलन को समझेंगे।
कॉम्प्लेक्स प्लेन में कर्व्स – कॉम्प्लेक्स एनालिसिस के गणितीय क्षेत्र में कन्टूर इंटीग्रेशन कॉम्प्लेक्स प्लेन में पथ के साथ कुछ इंटीग्रल्स के मूल्यांकन की एक विधि है।कंटूर समाकल,अवशेषों की गणना,सम्मिश्र विश्लेषण की एक विधि से निकटता से संबंधित है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Contour Integration
2.सम्मिश्र कन्टूर समाकलन उदाहरण (Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration Examples),कन्टूर समाकलन साॅल्वड उदाहरण (Contour Integration Solved Examples)-
Example-1.फलन \frac{e^{i z^{2}}}{z} को उपयुक्त परिरेखा पर समाकलन करते हुए सिद्ध कीजिए कि \int_{0}^{\infty} \frac{\sin x^{2}}{x} d x=\frac{\pi}{4} तथा निगमन कीजिए कि \int_{0}^{\infty} \frac{\sin x}{x} d x=\frac{\pi}{2}
(By integrating \frac{e^{i z^{2}}}{z} round a suitable contour,prove that \int_{0}^{\infty} \frac{\sin x^{2}}{x} d x=\frac{\pi}{4} ,also deduct that \int_{0}^{\infty} \frac{\sin x}{x} d x=\frac{\pi}{2} .)
Solution-माना \int_{c} \frac{e^{i z^{2}}}{z} d z=\int_{c} f(z) d z
जहां C वृत्त का भाग है। अतः अवशेष प्रमेय से-
\int_{C} f(z) d z=\int_{\rho}^{R} f(x) d x+\int_{\Gamma} f(z) d z+\int_{R}^{\rho} f(i y) i dy+\int_{\gamma} f(z) d z=0.....(1)
अब \left|\int_{\Gamma} f(z) d z\right| \leq \int_{0}^{\frac{\pi}{2}} \left| \frac{\exp \left(i R e^{i 2 \theta}\right)}{R e^{i \theta}} R i e^{i \theta} \right| d \theta \\ \leq \int_{0}^{\frac{\pi}{2}} e^{-R^{2} \cdot \sin 2 \theta} d \theta \rightarrow 0 जब R \rightarrow \infty \\ \int_{\gamma} f(z) d z=\int_{\frac{\pi}{2}}^{0} \frac{exp\left(i e^{2} e^{(i2 \theta)}\right)}{\rho e^{ i \theta}} e i e^{i \theta} d \theta \\ =i \int_{\frac{\pi}{2}}^{0}[1+0(\rho)] d \theta \\ =-\frac{i \pi}{2}
अतः जब R \rightarrow \infty, \rho \rightarrow 0, समीकरण (1) से-
\int_{0}^{\infty} f(x) d x+\int_{\infty}^{0} f(i y) i d y-i \frac{\pi}{2}=0 \\ \Rightarrow \int_{0}^{\infty} \frac{e^{i x^{2}}}{x} d x-\int_{0}^{\infty} \frac{e^{-i y^{2}}}{i y} d y=\frac{i \pi}{2} \\ \Rightarrow \int_{0}^{\infty} \frac{e^{i x^{2}}-e^{-i x^{2}}}{x} d x=\frac{i \pi}{2} \\ \Rightarrow \int_{0}^{\infty} \frac{2 i \sin x^{2}}{x} d x=\frac{i \pi}{2} \\ \Rightarrow \int_{0}^{\infty} \frac{\sin x^{2}}{x} d x=\frac{\pi}{4} \cdots(2)
अब x=\sqrt{t} , समीकरण (2) में रखने पर-
\int_{0}^{\infty} \frac{\sin t}{\sqrt{t}} \cdot \frac{d t}{2 \sqrt{t}}=\frac{\pi}{4} \\ \Rightarrow \int \frac{\ sin t}{t} d t= \frac{\pi}{2}
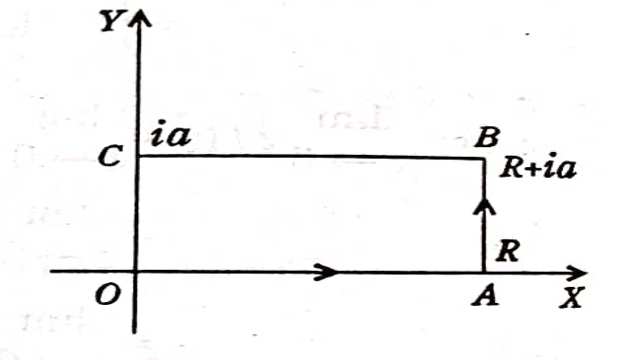
Example-2.एक आयत जिसके सम्मिश्र तल में शीर्ष बिन्दु O,R,R+ia,ia हैं,पर e^{-z^{2}} का समाकलन करते हुए सिद्ध कीजिए कि
(By integrating e^{-z^{2}} round the rectangle whose vertices are O,R,R+ia,ia show that):
(i) \int_{0}^{\infty} e^{-x^{2}} \cos (2 a x) d x=\frac{-e^{a^{2}}}{2} \sqrt{\pi} \\ (ii) \int_{0}^{\infty} e^{-x^{2}} \sin (2 a x) d x=e^{-a^{2}} \int_{0}^{a} e^{y^{2}} d y
Solution–\int_{C} e^{-z^{2}} d z=\int_{C} f(z) d z
जहां C एक आयत है जिसकी भुजाएं हैं x=0,x=R,y=0,y=a
f(z) के अन्दर C का कोई अनन्तक नहीं है अतः अवशेष प्रमेय से-
\int f(z) d z=\int_{0}^{R} f(x) d x+\int_{0}^{a} f(R+i y) i d y+\int_{R}^{0} f(x+i a) d x +\int_{a} f(iy) i dy=0 \\ \Rightarrow I_{1}+I_{2}+I_{3}+I_{4}=0 \cdots (1)
अब \left|I_{1}\right| =\int_{0}^{a} e^{-(R+i y)^{2}} i d y \mid \\ \leq \int_{0}^{a} \mid e^{-R^{2}+y^{2}-2 i R y} i \mid d y \\ \leq \int_{0}^{a} e^{-R^{2}} \cdot e^{y^{2}} d y \rightarrow 0 जब R \rightarrow \infty
जब R \rightarrow 0 तो समीकरण (1) से-
\int_{0}^{\infty} e^{-x^{2}} d x + \int_{0}^{\infty} e^{-(x+i a)^{2}} d x+\int_{a}^{0} i e^{y^{2}} d y=0 \\ \Rightarrow e^{a^{2}} \int_{0}^{\infty} e^{-x^{2}} \cdot e^{-i 2 a x} d x+i \int_{0}^{a} e^{y^{2}} d y=\frac{\sqrt{\pi}}{2}
दोनों पक्षों के वास्तविक और काल्पनिक भागों की तुलना करने पर-
e^{a^{2}} \cdot \int_{0}^{\infty} e^{-x^{2}} \cdot \cos 2 a x d x=\frac{\sqrt{\pi}}{2}
तथा -e^{a^{2}} \int_{0}^{\infty} e^{-x^{2}} \sin 2 a x d x+\int_{0}^{a} e^{y^{2}} d y=0 \\ \Rightarrow \int_{0}^{\infty} e^{-x^{2}} \sin 2 a x=e^{-a^{2}} \int_{0}^{a} e^{y^{2}} d y
Example-3.फलन \log \left(1-e^{2 i z}\right) को उपयुक्त परिरेखा पर समाकलन करते हुए सिद्ध कीजिए कि
(Integrating \log \left(1-e^{2 i z}\right) round a suitable contour, prove that):
\int_{0}^{\pi} \log (\sin x) d x=-\pi \log 2
Solution–\int_{C} \log \left(1-e^{i 2 z}\right) d z=\int_{C} f(z) d z
जहां C आयत है अतः अवशेष प्रमेय से-
\int_{c} f(z) d z=\int_{\rho_{1}}^{\pi-\rho_{2}} f(x) d x+\int_{\gamma_{2}} f(z) d z+\int_{\rho_{2}}^{n} f(\pi+i y) d y +\int_{\pi}^{0} f(x+i n) d x+\int_{n}^{\rho_{1}} f(i y) id y +\int_{\gamma_{1}} f(z) d z=0 \\ I_{1}+I_{2}+I_{3} +I_{4} +I_{5}+I_{6}=0 \\ I_{3}=\int_{\rho_{2}}^{n} \log \left(1-e^{2 i(\pi+i y)} \right)i d y=\int_{\rho_{2}}^{n} i \log \left(1-e^{-2 y}\right) d y
तथा I_{5}=\int_{n}^{\rho_{1}} \log \left(1-e^{2 i(i y)}\right) i d y=\int_{n}^{\rho_{1}} i \log \left(1-e^{-2 y}\right) d y
जब n \rightarrow \infty, \quad \rho_{1} \rightarrow 0, \rho_{2} \rightarrow 0 \\ I_{3}+I_{5} =\int_{0}^{\infty} i \log \left(1-e^{-2 y}\right) d y+\int_{\infty}^{0} i \log \left(1-e^{-2 y}\right) d y \\ =\int_{0}^{\infty} i \log \left(1-e^{-2 y}\right) d y-\int_{0}^{\infty} i \log \left(1-e^{-2 y}\right) d y=0 \\ \lim _{z \rightarrow 0} z f(z) =\lim _{z \rightarrow 0} z \log \left(1-e^{i 2 z}\right) \\ =\lim _{z \rightarrow 0} \frac{\log \left(1-e^{i 2 z}\right)}{\frac{1}{z}}\left(\frac{\infty}{\infty} \text { form }\right) \\ =\lim _{z \rightarrow 0} \frac{-2 i e^{i 2 z}\left\{\frac{1}{\left(1-e^{i 2 z} \right)}\right\}}{\left(-1 / z^{2}\right)} (\text { DL Hospital Rule} ) \\ = \lim _{z \rightarrow 0} \frac{2 i z^{2} e^{i 2 z}}{1-e^{i 2 z}}\left(\frac{0}{0} \text { form } \right) \\ =\lim_{z \rightarrow 0} \frac{4 i z e^{i 2 z}+2 i z^{2} e^{i 2} z \cdot 2 i}{-2 i \cdot e^{i 2 z}} (\text { DL Hospital Rule} )\\ =0 \\ \lim _{\rho_{1} \rightarrow 0} I_{6}=0
इसी प्रकार
I_{2} \rightarrow 0 जब \rho_{2} \rightarrow 0 \\ I_{4} =\int_{\pi}^{0} \log \left(1-e^{i 2(x+i n)}\right) d x \\ =\int_{\pi}^{0} \log \left(1-e^{i 2 x} e^{-2 x}\right) d x \rightarrow 0 जब n \rightarrow \infty
n \rightarrow \infty, \quad \rho_{1} \rightarrow 0, \rho_{2} \rightarrow 0 तब समीकरण (1) से-
\int_{0}^{\pi} f(x) d x=0 या \int_{0}^{\pi} \log\left(1-e^{i 2 x}\right)=0 \\ \int_{0}^{\pi} \log \left\{e^{i x}\left(e^{-i x}-e^{i x}\right)\right\} d x=0
या \int_{0}^{\pi} \left\{ \int e^{i x}(-2 i \sin x) \right\} d x=0 \\ \Rightarrow \int_{0}^{\pi} i x d x+\int_{0}^{\pi} \log 2 d x+\int_{0}^{\pi} \log (-i) d x+\int_{0}^{\pi} \log (\sin x) d x=0 \\ \Rightarrow i \frac{\pi^{2}}{2}+\pi \log 2+(-i \frac {\pi}{2}) \pi+\int_{0}^{\pi} \log (\sin x)=0 \\ \Rightarrow \int_{0}^{\pi} \log (\sin x) d x=-\pi \log 2
Example-4.यदि a>0 तो सिद्ध कीजिए कि (a>0 then prove that):
P \int_{-\infty}^{\infty} \frac{\cos x}{a^{2}-x^{2}} d x=\frac{\pi}{a} \sin a
Solution–\int_{c} f(z) d z=\int_{c} \frac{e^{i z}}{a^{2}-z^{2}} d z
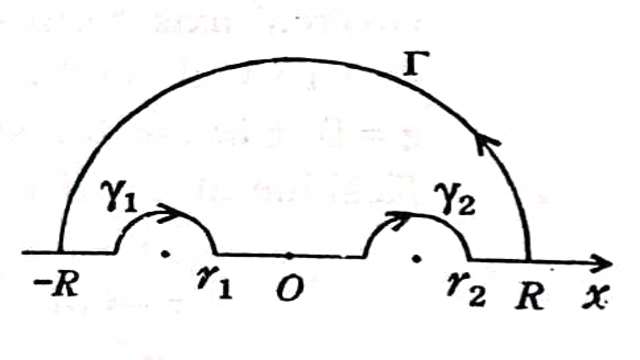
जहां C परिरेखा है जिसमें R त्रिज्या का वृहत अर्द्ध वृत्त \Gamma शामिल है तथा z=a तथा z=-a है। \gamma_{1} तथा \gamma_{2} छोटे अर्द्धवृत्त हैं जिनकी त्रिज्या r_{1} तथा r_{2} व केन्द्र z=-a और z=a है।
z=a तथा z=-a पर दन्तुरण द्वारा टाल दिया गया है अतः कोशी अवशेष प्रमेय से-
\int_{C} f(z) d z=\int_{\Gamma} f(z) d z+\int_{-R}^{-\left(a+r_{1}\right)} f(x) d x+\int_{\gamma_{1}} f(z) d z+\int_{-(a-r_{1})}^{a-r_{2}} f(x) d x +\int_{\gamma_{2}} f(z) d z+\int_{a+r_{2}}^{R} f(x) d x=0 .....(1)
जब z \rightarrow \infty तो \frac{1}{a^{2}-z^{2}} \rightarrow 0
अतः जोरदां उपप्रमेय से-
\lim _{R \rightarrow \infty} \int_{\Gamma} f(z) d z =0 \\ \lim _{z \rightarrow-a}(a+z) f(z) =\lim _{z \rightarrow -a} \frac{e^ {i z}}{a-z}-\frac{e^{-i a}}{2 a} \\ \lim _{r_{1} \rightarrow 0} \int_{\gamma_{1}} f(z) d z =i \frac{e^{-i a}}{2 a}(0-\pi) \\ =-\frac{i \pi}{2 a}{e}^{-i a}
इसी प्रकार \lim _{r_{2} \rightarrow 0} \int_{\gamma_{2}} f(z) d z=i \frac{\pi}{2 a} e^{i a}
जब R \rightarrow \infty, r_{1} \rightarrow 0, r_{2} \rightarrow 0 तो समीकरण (1) से-
\int_{-\infty}^{-a} f(x) d x+\left(-i \frac{\pi}{2 a} e^{-i a}\right)+\int_{-a}^{a} f(x) d x+\frac{i \pi}{2 a} e^{i a}+\int_{a} ^{\infty} f(x) d x=0 \\ \Rightarrow p \int_{-\infty}^{\infty} f(x) d x=-i \frac{\pi}{2 a}\left(e^{i a}-e^{-i a}\right) \\ \Rightarrow p \int_{-\infty}^{\infty} \frac{e^{i x}}{a^{2}-x^{2}} d x=\frac{\pi}{a} \sin a
दोनों पक्षों के वास्तविक और काल्पनिक भागों की तुलना करने पर-
p \int_{-\infty}^{\infty} \frac{\cos x}{a^{2}-x^{2}} d x=\frac{\pi}{a} \sin a
तथा P \int_{-\infty}^{\infty} \frac{\sin x}{a^{2}-x^{2}} d x=0
Example-5.सिद्ध कीजिए कि (prove that):
\int_{0}^{\infty} \cos x^{2} dx =\int_{0}^{\infty} \sin x^{2} d x=\frac{1}{2} \sqrt{\frac{\pi}{2}}
Solution–\int_{c} f(z) d z =\int_{c}{e}^{-z^{2}} d z
जहां C वृत्त का चाप है। अतः कोशी अवशेष प्रमेय से-
\int_{C} f(z) d z=\int_{O A} f(x) d x+\int_{A B} f(z) d z+\int_{B O} f(z) d z=0.....(1) \\ \left|\int_{A B} f(z) d z\right|= \left|\int_{\Gamma} f(z) d z\right| \\ \leq \int_{0}^{\alpha}\left|\exp \left(-{R}^{2} e^{i 2 \theta}\right) R i e^{i \theta} \right| d \theta \\ \leq \int_{0}^{\alpha} e^{-R^{2} \cos 2 \theta} R d \theta \\ \leq \frac{1}{2} R \int_{\frac{\pi}{2}-2 \alpha}^{\frac{\pi}{2}} \exp \left(-R^{2} \sin \phi\right) d \phi[2 \theta=\frac{\pi}{2}- \phi] \\ \leq \frac{1}{2} R \int_{\frac{\pi}{2}-2 \alpha}^{\frac{\pi}{2}} e x p\left\{ -\left(\frac{2 R^{2}}{\pi \phi}\right)\right\} d \phi
[जोरदां असमिका से]
\leq \frac{\pi}{4 R}\left[exp \left\{-\frac{2 R^{2}}{\pi}\left(\frac{\pi}{2}-2 \alpha\right)\right\}-\bar{e}^{R^{2}}\right] \rightarrow 0
जब R \rightarrow \infty जबकि \alpha \leq \frac{\pi}{4}
अतः R \rightarrow \infty समीकरण (1) से-
\int_{0}^{\infty} e^{-x^{2}} d x-\int_{0}^{\infty} \exp \left(-r^{2} e^{i 2 \alpha}\right) e^{i \alpha} dr=0 \\ \Rightarrow \int_{0}^{\infty} e^{-x^{2} \cos 2 \alpha} e^{-i x^{2} \sin 2 \alpha} d x=e^{-i \alpha} \int_{0}^{\infty} e^{-x^{2}} d x \\ \Rightarrow \int_{0}^{\infty} e^{-x^{2} \cos 2 \alpha} e^{-i x^{2} \sin 2 \alpha} d x=\frac{\sqrt{\pi}}{2} e^{-i \alpha}
दोनों पक्षों के वास्तविक और काल्पनिक भागों की तुलना करने पर-
\int_{0}^{\infty} e^{-x^{2} \cos 2 \alpha}{2} \cos \left(x^{2} \sin 2 \alpha\right) d x= \frac{\sqrt{\pi}}{2} \cos \alpha
तथा \int_{0}^{\infty} e^{-x^{2} \cos 2 \alpha} \sin \left(x^{2} \sin 2 \alpha\right) d x=\frac{\sqrt{\pi}}{2} \sin \alpha
\alpha=\frac{\pi}{4} रखने पर-
\int_{0}^{\infty} \cos x^{2} d x=\frac{1}{2} \sqrt{\frac{\pi}{2}}, \int_{0}^{\infty} \sin x^{2} d x=\frac{1}{2} \sqrt{\frac{\pi}{2}}
अतः \int_{0}^{\infty} \cos x^{2} d x=\int_{0}^{\infty} \sin x^{2} d x=\frac{1}{2} \sqrt{\frac{\pi}{2}}
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र कन्टूर समाकलन उदाहरण (Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration) को समझ सकते हैं।
3.सम्मिश्र कन्टूर समाकलन की समस्याएं (Complex Contour Integration Problems),कन्टूर समाकलन की समस्याएं,परिरेखा समाकलन की समस्याएं (Contour Integration Problems)-
मान ज्ञात कीजिए (Evaluate):
(1) \int_{-\infty}^{\infty} \frac{\cos x d x}{\left(x^{2}+a^{2}\right)\left(x^{2}+b^{2}\right)}, \quad(a>b>0) \\ (2) \int_{0}^{\infty} \frac{\cos x}{\left(x^{2}+a^{2}\right)^{2}} d x (a>0)
(3.)यदि m>0 तो सिद्ध कीजिए कि (If m>0 then prove that):
P \int_{-\infty}^{\infty} \frac{\cos m x}{x-b} d x=-\pi \sin (m b)
(4.)मान ज्ञात कीजिए (Evaluate):
\int_{-\infty}^{\infty} \frac{x \sin \pi x}{x^{2}+2 x+5} d x
उत्तर (Answers): (1)\frac{\pi}{a^{2}-b^{2}}\left(\frac{e^{-b}}{b}-\frac{e^{-a}}{a}\right) \\ (2)\frac{\pi}{4 a^{3}}(1-m a) e^{-m a} \\ (4) -\pi e^{-2 \pi}
उपर्युक्त सवालों को हल करने पर सम्मिश्र कन्टूर समाकलन उदाहरण (Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration) को ठीक से समझ सकते हैं।
Also Read This Article:-Solve Complex Contour Integration
4.सम्मिश्र कन्टूर समाकलन उदाहरण (Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration) में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.सम्मिश्र विश्लेषण में कन्टूर समाकलन क्या है? (What is contour integration in complex analysis?)
उत्तर-कन्टूर समाकलन सम्मिश्र समतल में दिए गए कन्टूर के आसपास कन्टूर समाकल के मूल्यों की गणना करने की प्रक्रिया है।होलोमोर्फिक फलनों की वास्तव में आश्चर्यजनक गुणधर्म के परिणामस्वरूप, कन्टूर के अंदर सम्मिश्र अवशेषों के मूल्यों को संक्षेप में आसानी से इस तरह के समाकल की गणना की जा सकती है।
प्रश्न:2.आप सम्मिश्र कन्टूर समाकलन को कैसे हल करते हैं? (How do you solve complex contour integration?)
उत्तर-विभिन्न प्रकार के निश्चित समाकलनों का मान निकालने के लिए दन्तुरण सहित या दन्तुरण रहित वृत्ताकार या अर्धवृत्ताकार परिरेखाओं का प्रयोग किया जाता है।इसके अलावा कुछ प्रकार के समाकलनों का मान ज्ञात करने के लिए दन्तुरण सहित या दन्तुरण रहित परिरेखाओं जैसे वृत्त का चतुर्थांश, वृत्त खण्ड,आयत आदि का प्रयोग भी करते हैं।
प्रश्न:3.आप सम्मिश्र समाकलन कैसे करते हैं? (How do you do complex integration?)
उत्तर-कन्टूर मीट (Meet) सिंगुलेरिटीज (singularities)। याद रखें कि सम्मिश्र समतल में एक बंद कन्टूर के साथ एक फलन के समाकल मूल्यांकन में, हम हमेशा कन्टूर को स्थानांतरित कर सकते हैं।
वक्र के अन्दर स्थित अनन्तकों पर कोशी अवशेष प्रमेय द्वारा अवशेष ज्ञात करके उनका योगफल परिरेखा समाकलन होता है।
प्रश्न:4.सम्मिश्र रेखा समाकल क्या है? (What is complex line integral?)
सम्मिश्र रेखा समाकल की परिभाषा
उत्तर-माना एक सम्मिश्र चर का एक संतत सम्मिश्र-मूल्यवान फ़ंक्शन है, और C को सम्मिश्र समतल पैरामीट्रिज्ड द्वारा एक चिकनी वक्र बनाते हैं Z(t) =x(t)+iy(t) जहां t,a और b के बीच परिवर्तित होता है।फिर C के ऊपर f की सम्मिश्र लाइन इंटीग्रल द्वारा दी गई है।
प्रश्न:5.कन्टूर समाकल को कैसे हल करें? (How to Solve Contour Integrals?)
उत्तर-कोशी अवशेष प्रमेय की सहायता से वास्तविक निश्चित समाकलों का मूल्यांकन आसानी से किया जा सकता है। इसके लिए हम उचित परिरेखा का चयन इस प्रकार करते हैं कि फलन की समस्त विचित्रताएं C के अन्दर रहें।इन विचित्र बिन्दुओं पर अवशेष का मूल्यांकन करके तथा कोशी अवशेष प्रमेय का उपयोग करके समाकलन का मूल्यांकन करते हैं।
प्रश्न:6.कन्टूर समाकलन प्रकार 2 (Contour Integration Type 2),कन्टूर समाकलन प्रकार 3 (Contour Integration Type 3)
उत्तर-यदि फलन के अनन्तक वास्तविक अक्ष पर स्थित हैं परिरेखा पर फलन का संभालने नहीं किया जा सकता है। लेकिन इन अनन्तकों को टालने के लिए,इन अनन्तकों को केन्द्र मानते हुए छोटी त्रिज्या वाले अर्धवृत्तों का निर्माण करते हैं।इस प्रक्रिया को अर्धवृत्तीय परिरेखा का दन्तुरण (indenting) कहते हैं।इस रूपान्तरित (modified) परिरेखा पर फलन विश्लेषिक रहता है तथा कोशी अवशेष प्रमेय तथा अन्य प्रमेयों की सहायता से फलन का समाकलन किया जा सकता है।
बहुमानी फलनों का समाकलन भी अर्धवृत्तीय परिरेखा के दन्तुरण विधि द्वारा किया जा सकता है। इसमें शाखा बिन्दु को उसी बिन्दु पर केन्द्रित उपरि अर्धतल में स्थित छोटी त्रिज्या वाले वृत्त द्वारा टाला जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र कन्टूर समाकलन उदाहरण का परिचय (Introduction to Complex Contour Integration Examples),कन्टूर समाकलन,परिरेखा समाकलन (Contour Integration) को आसानी समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |