Area of Quadrilateral
1.चतुर्भुज का क्षेत्रफल (Area of Quadrilateral),निर्देशांक ज्यामिति में चतुर्भुज का क्षेत्रफल(Area of Quadrilateral Coordinate Geometry):
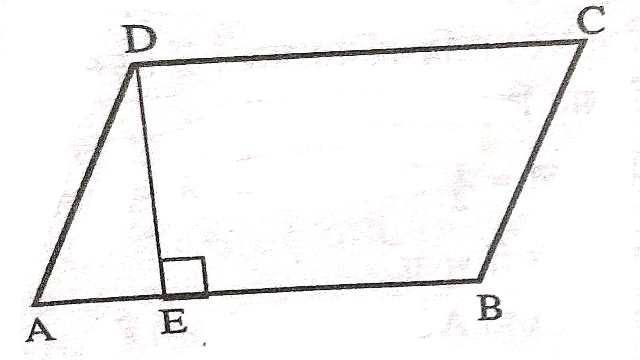
चतुर्भुज का क्षेत्रफल (Area of Quadrilateral) :समतलीय आकृति कहलाती है।किसी चतुर्भुज को उसके विवरणों द्वारा दो त्रिभुजों में विभाजित किया जा सकता है।चित्रानुसार चतुर्भुज ABCD को विकर्ण AC दो त्रिभुजों \triangle ABC एवं \triangle ACD त्रिभुज में विभक्त करता है।अतः चतुर्भुज ABCD का क्षेत्रफल दोनों त्रिभुजों के क्षेत्रफल के योग के बराबर होगा।चतुर्भुज के शीर्ष B एवं D से विकर्ण AC पर लम्ब क्रमशः BE एवं DF खींचिए।
अतः. \triangle ABC का क्षेत्रफल=\frac{1}{2} \times AC \times BE
तथा \triangle ACD का क्षेत्रफल=\frac{1}{2} \times AC \times DF
अर्थात् चतुर्भुज ABCD का.क्षेत्रफल=\triangle ABC का क्षेत्रफल+\triangle ACD का क्षेत्रफल
=\frac{1}{2} \times AC \times BE +\frac{1}{2} \times AC \times DF \\ =\frac{1}{2} \times AC \times (BE+DF)
अतः चतुर्भुज का क्षेत्रफल=\frac{1}{2} \times \text{ विकर्ण } \times \text{ (विकर्ण पर डाले गए लंबो का योग)}
समान्तर चतुर्भुज का क्षेत्रफल (Area of Parallelogram):
ऐसा चतुर्भुज जिसकी सम्मुख भुजाएं परस्पर समांतर एवं समान हो समांतर चतुर्भुज कहलाता है।
(1.)समांतर चतुर्भुज का क्षेत्रफल=आधार × ऊँचाई
=AB × DE
(2.)समान्तर चतुर्भुज का विकर्ण चतुर्भुज को दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करता है।
अतः समांतर चतुर्भुज का क्षेत्रफल=2 ×(\triangle ABC का क्षेत्रफल)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Baudhayan Theorem
2.चतुर्भुज का क्षेत्रफल के उदाहरण (Area of Quadrilateral Examples):
Example:1.चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके विकर्ण की लम्बाई 12 सेमी है तथा सम्मुख शीर्षों से डाले गए लम्बों की लम्बाई क्रमशः 7 सेमी एवं 8 सेमी है।
Solution:चतुर्भुज का क्षेत्रफल=\frac{1}{2} \times \text{ विकर्ण } \times \text{ (विकर्ण पर डाले गए लंबो का योग)} \\ =\frac{1}{2} \times 12 \times (7+8) \\ =\frac{1}{2} \times 12 \times 15 =90 वर्ग सेमी
Example:2.एक समांतर चतुर्भुजाकार खेल के मैदान का क्षेत्रफल 2000 वर्ग मीटर है।यदि इसका आधार 50 मीटर हो तो मैदान की ऊंचाई ज्ञात कीजिए।
Solution:समांतर चतुर्भुज का क्षेत्रफल=आधार × ऊंचाई
\Rightarrow 2000=50 × \text { ऊंचाई } \\ \Rightarrow \text { ऊंचाई } =\frac{2000}{50} \\ \Rightarrow \text { ऊंचाई } =40 मीटर
Example:3.चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाएं क्रमशः AB=3 सेमी,BC=4 सेमी,CD=6 सेमी एवं DA=5 सेमी है तथा विकर्ण AC=5 सेमी है।
Solution:चतुर्भुज ABCD का क्षेत्रफल=\triangle ABC का क्षेत्रफल+\triangle ACD का क्षेत्रफल
\triangle ABC में AB=3 सेमी,BC=4 सेमी,AC=5 सेमी
अतः का अर्द्ध परिमाप s=\frac{3+4+5}{2}=\frac{12}{2} \\ \Rightarrow s=6
\triangle ABC का क्षेत्रफल=\sqrt{s(s-a)(s-b)(s-c)} \\ =\sqrt{6(6-3)(6-4)(6-5)} \\ =\sqrt{6 \times 3 \times 2 \times 1} \\ =\sqrt{36} \\ ar( \triangle ABC )=6 वर्ग सेमी
में AC=5 सेमी,CD=6 सेमी,DA=5 सेमी
अतः अर्द्ध परिमाप s=\frac{5+6+5}{2} \\ \Rightarrow s=8
\triangle ACD का क्षेत्रफल=\sqrt{s(s-a)(s-b)(s-c)} \\ =\sqrt{8(8-5)(8-6)(8-5)} \\ =\sqrt{8 \times 3 \times 2 \times 3} \\ =\sqrt{144} \\ =12 वर्ग सेमी
अतः चतुर्भुज का ABCD का क्षेत्रफल=6+12=18 वर्ग सेमी
Example:4.चतुर्भुज. का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाएं क्रमशः 9सेमी,40 सेमी,28 सेमी एवं 15 सेमी है तथा इसकी प्रथम दो भुजाओं के मध्य समकोण है।
Solution:विकर्ण AC=\sqrt{ \text{ आधार }^{2}+\text{ लंब }^{2}} \\ =\sqrt{AB^{2}+BC^{2}} \\ =\sqrt{9^{2}+40^{2}} \\=\sqrt{81+1600} \\ =\sqrt{1681} \\ \Rightarrow AC=41
चतुर्भुज ABCD का क्षेत्रफल=\triangle ABC का क्षेत्रफल+\triangle ACD का क्षेत्रफल
\triangle ABC का क्षेत्रफल=\frac{1}{2} \times \text{ आधार }× \text{ ऊँचाई } \\=\frac{1}{2} \times AB \times BC \\ =\frac{1}{2} \times 9 \times 40 \\ \Rightarrow ar( \triangle ABC )=180 वर्ग सेमी
\triangle ACD में AC=41सेमी,CD=28 सेमी,AD=15 सेमी
अतः अर्द्ध परिमाप s=\frac{41+28+15}{2}=\frac{84}{2} \\ \Rightarrow s=42
\triangle ACD का क्षेत्रफल=\sqrt{s(s-a)(s-b)(s-c)} \\ =\sqrt{42(42-41)(42-28)(42-15)} \\ =\sqrt{42 \times 1 \times 14 \times 27} \\ =\sqrt{2 \times 3 \times 7 \times 2 \times 7 \times 3 \times 3 \times 3}\\ =\sqrt{2 \times 2 \times 3 \times 3 \times 3 \times 3 \times 7 \times 7}\\ =2 \times 3 \times 3 \times 7 \\ ar( \triangle ACD )=126 वर्ग सेमी
चतुर्भुज ABCD का क्षेत्रफल=180+126=306 वर्गसेमी
Example:5.एक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो आसन्न भुजाएं क्रमशः 50 सेमी एवं 40 सेमी हो तथा विकर्ण 30 सेमी हो।
Solution:समांतर चतुर्भुज का क्षेत्रफल=2 × त्रिभुज का क्षेत्रफल
त्रिभुज में a=50 सेमी,b=40 सेमी,c=30 सेमी
अर्द्ध परिमाप s=\frac{50+40+30}{2}=\frac{120}{2} \\ \Rightarrow s=60 सेमी
त्रिभुज का क्षेत्रफल=\sqrt{s(s-a)(s-b)(s-c)} \\ =\sqrt{60(60-50)(60-40)(60-30)} \\ =\sqrt{60 \times 10 \times 20 \times 30} \\ =\sqrt{2 \times 3 \times 2 \times 3 \times 10 \times 10 \times 10 \times 10}\\ =2 \times 3 \times 10 \times 10 \\ =600 वर्ग सेमी
अतः चतुर्भुज का क्षेत्रफल=2 × 600
=1200 वर्गसेमी
Example;:6.समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके एक विकर्ण की लम्बाई 52 सेमी तथा विकर्ण के सम्मुख शीर्षों से. लम्बों की दूरियां क्रमशः 3.5 सेमी है।
Solution:समान्तर चतुर्भुज का क्षेत्रफल
=\frac{1}{2} \times \text{ विकर्ण } \times \text{ (विकर्ण पर डाले गए लंबो का योग)} \\ =\frac{1}{2} \times 5.2 \times (3.5+3.5) \\ =\frac{1}{2} \times 5.2 \times 7 =18.2 वर्ग सेमी
Example:7.समान्तर चतुर्भुज का क्षेत्रफल का आधार 18 मीटर एवं क्षेत्रफल 174.60 वर्ग मीटर हो तो इसकी ऊंचाई लिखिए।
Solution:समान्तर चतुर्भुज का क्षेत्रफल=आधार × ऊँचाई
\Rightarrow 174.60=18 × \text { ऊंचाई } \\ \Rightarrow \text { ऊंचाई } =\frac{174.60}{18} \\ \Rightarrow \text { ऊंचाई } =9.7 मीटर
Example:8.दो विभिन्न रंगों के कपड़ों के त्रिभुजाकार टुकड़ों को जोड़कर एक छाता बनाया जाता है।प्रत्येक टुकड़े की माप 20 सेमी,50 सेमी और 50 सेमी है।छाते में कितना कपड़ा लगा है?
Solution:त्रिभुज में a=20 सेमी,b=50 सेमी,c=50 सेमी
अर्ध परिमाप s=\frac{a+b+c}{2} \\ =\frac{20+50+50}{2}=\frac{120}{2} \\ \Rightarrow s=60 सेमी
त्रिभुज का क्षेत्रफल=\sqrt{s(s-a)(s-b)(s-c)} \\ =\sqrt{60(60-20)(60-50)(60-50)} \\ =\sqrt{60 \times 40 \times 10 \times 10} \\ =\sqrt{6 \times 4 \times 10 \times 10 \times 10 \times 10 }\\ =2 \times 10 \times 10 \sqrt{6} \\ =200\sqrt{6} वर्ग सेमी
10 त्रिभुजाकार टुकड़ों अर्थात छाते में लगे कपड़े का क्षेत्रफल=10 \times 200 \sqrt{6} \\ =2000 \sqrt{6} वर्गसेमी
Example:9.दी गई आकृति में समांतर चतुर्भुज ABCD का क्षेत्रफल 17.49 वर्गसेमी है।यदि लम्ब DE=3.3 सेमी हो तो AB भुजा की.लंबाई ज्ञात कीजिए।
Solution:समान्तर चतुर्भुज का क्षेत्रफल=आधार × ऊँचाई
17.49=AB \times DE \\ 17.49=AB × 3.3 \\ \Rightarrow AB=\frac{17.49}{3.3} \\ =5.3 सेमी
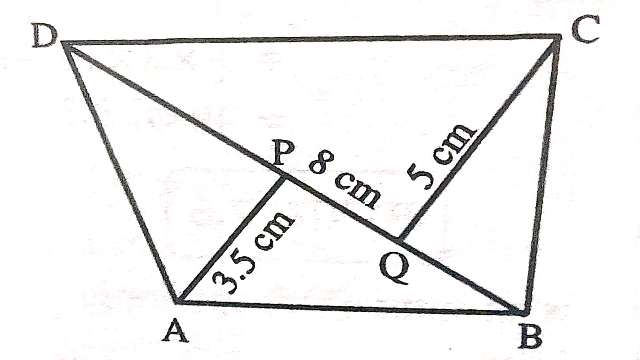
Example:10.चतुर्भुज ABCD में विकर्ण BD=8 सेमी अन्तर्लम्ब AP=3.5 सेमी और अन्तर्लम्ब CQ=5 सेमी है,तो चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
Solution:
चतुर्भुज ABCD का क्षेत्रफल=\frac{1}{2} \times \text{ विकर्ण } \times \text{ (विकर्ण पर डाले गए लंबो का योग)} \\=\frac{1}{2} \times BD \times (AP+QC)\\ =\frac{1}{2} \times 8 \times (3.5+5) \\ = 4 \times 8.5 =34 वर्ग सेमी
उपर्युक्त उदाहरणों के द्वारा चतुर्भुज का क्षेत्रफल (Area of Quadrilateral),निर्देशांक ज्यामिति में चतुर्भुज का क्षेत्रफल(Area of Quadrilateral Coordinate Geometry) को समझ सकते हैं।
3.चतुर्भुज का क्षेत्रफल की समस्याएं (Area of Quadrilateral Problems):
(1.)एक चतुर्भुज का विकर्ण 10 सेमी एवं विकर्ण पर सम्मुख शीर्षों से डालें गए लम्बों की लम्बाई क्रमशः 6 सेमी एवं 4 सेमी हो तो चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
(2.) एक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी ऊंचाई 15 मीटर तथा आधार 10 मीटर हो।
(3.) किसी समांतर चतुर्भुज की दो आसन्न भुजाएं क्रमशः 5 सेमी एवं 4 सेमी है तथा विकर्ण 7 सेमी है।समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर (Answers):(1.)50 वर्गसेमी (2.)150 वर्गमीटर (3.)8 \sqrt{6} वर्गसेमी
उपर्युक्त सवालों को हल करने पर चतुर्भुज का क्षेत्रफल (Area of Quadrilateral),निर्देशांक ज्यामिति में चतुर्भुज का क्षेत्रफल(Area of Quadrilateral Coordinate Geometry) को ठीक से समझ सकते हैं।
Also Read This Article:-Theorem of Area of Parallelogram
4.चतुर्भुज का क्षेत्रफल (Area of Quadrilateral),निर्देशांक ज्यामिति में चतुर्भुज का क्षेत्रफल(Area of Quadrilateral Coordinate Geometry) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.चतुर्भुज के क्षेत्रफल का सूत्र क्या है? (What is the formula of the Area of Quadrilateral?):
उत्तर:यदि विकर्ण और शीर्षों से लंबों की लंबाई दी गई है, तो चतुर्भुज के क्षेत्रफल की गणना इस प्रकार की जाती है: चतुर्भुज का क्षेत्रफल = (½) × विकर्ण लंबाई × शेष दो शीर्षों से खींचे गए लंबों की लंबाई का योग।
[Area of quadrilateral = (½) × diagonal length × sum of the length of the perpendiculars drawn from the remaining two vertices]
प्रश्न:2.चतुर्भुज ABCD का क्षेत्रफल कितना है? (What is the area of quadrilateral ABCD?):
उत्तर:उपरोक्त आकृति से,चतुर्भुज ABCD का क्षेत्रफल= ∆BCD का क्षेत्रफल + ∆ABD का क्षेत्रफल।अत: चतुर्भुज ABCD का क्षेत्रफल =(\frac{1}{2}) × d × h_{1}+ (\frac{1}{2}) × d × h_{2}=(\frac{1}{2}) × d × (h_{1}+ h _{2} )
प्रश्न:3.आप एक अनियमित चतुर्भुज का क्षेत्रफल कैसे ज्ञात करते हैं? (How do you find the area of a irregular quadrilateral?):
उत्तर:ऐसे अनियमित चतुर्भुजों का क्षेत्रफल ज्ञात करने के लिए,तीन चरणों वाली रणनीति का पालन करें:
चतुर्भुज को दो त्रिभुजों में विभाजित करके एक विकर्ण की रचना करें जो ज्ञात अन्त: कोण (interior angle) को विचलित (disturb) न करे।
त्रिभजों के सूत्रों का उपयोग करके प्रत्येक त्रिभुज के क्षेत्रफल की गणना करें।
उन दोनों त्रिभुजों के क्षेत्रफलों को जोड़ें।यही चतुर्भुज का क्षेत्रफल होगा।
प्रश्न:4.चतुर्भुज का विकर्ण कौन सा है? (Which is diagonal of quadrilateral?):
उत्तर:एक चतुर्भुज के एक शीर्ष (one vertex) से विपरीत शीर्ष (opposite vertex) पर खींचा गया रेखाखंड चतुर्भुज का विकर्ण कहलाता है।एक सामान्य चतुर्भुज में दो विकर्ण होते हैं।
प्रश्न:5.एक अनियमित चतुर्भुज क्या है? (What is an irregular quadrilateral?):
उत्तर:एक अनियमित चतुर्भुज एक ऐसा चतुर्भुज है जो नियमित नहीं है,इसलिए इसकी सभी भुजाओं की लंबाई समान नहीं होती है।
प्रश्न:6.आप एक अनियमित चतुर्भुज को कैसे विभाजित करते हैं? (How do you divide an irregular quadrilateral?):
उत्तर:एक चतुर्भुज को समान क्षेत्रफलों में विभाजित करें
A से होकर MD के समानांतर एक रेखा खींचिए जो CD से P पर मिलती है।
B से होकर MC के समांतर एक रेखा खींचिए जो CD से Q पर मिलती है।
प्रश्न:7.क्या एक अनियमित चतुर्भुज में समकोण हो सकता है? (Can an irregular quadrilateral have a right angle?):
उत्तर:नहीं।एक चतुर्भुज के अन्त: और बाह्य दोनों कोणों (internal and external angles) का योग 360° होना चाहिए।चूँकि एक अधिक कोण (obtuse angle) 90° से अधिक और 180° से कम का कोण होता है,इसलिए 4 अधिक कोणों का योग कम से कम 360° से अधिक होना चाहिए,जो एक चतुर्भुज के लिए संभव नहीं है।
प्रश्न:8.चतुर्भुज आकृति कैसी दिखती है? (What is a quadrilateral shape look like?):
उत्तर:एक चतुर्भुज एक चार भुजाओं वाली द्वि-आयामी आकृति है।निम्नलिखित 2D आकार सभी चतुर्भुज हैं: वर्ग (square),आयत (rectangle), समचतुर्भुज (rhombus),समलंब (trapezium),समांतर चतुर्भुज (parallelogram) और पतंग (kite)।
प्रश्न:9.चतुर्भुज क्या है चित्र सहित समझाइए? (What is quadrilateral explain with diagram?):
उत्तर:ज्यामिति में,एक चतुर्भुज को एक बंद,दो-आयामी आकार के रूप में परिभाषित किया जा सकता है जिसमें चार सीधी भुजाएँ होती हैं।बहुभुज में चार शीर्ष (vertices) या कोने (corners) होती हैं।हम अपने आस-पास की विभिन्न चीजों में चतुर्भुज का आकार पा सकते हैं,जैसे शतरंज की बिसात (chess board),ताश के पत्तों का डेक (a deck of cards),पतंग (a kite),पॉपकॉर्न का टब (a tub of popcorn),साइन बोर्ड (a sign board) और तीर में (in an arrow)।
प्रश्न:10.क्या किसी चतुर्भुज का क्षेत्रफल और परिमाप समान हो सकता है? (Can a quadrilateral have the same area and perimeter?):
उत्तर:लेकिन अगर लंबाई और चौड़ाई दोनों विषम हैं,तो क्षेत्रफल विषम होगा,जिसका अर्थ है कि परिमाप (perimeter) का क्षेत्रफल के समान होना असंभव है।किनारों (edges) के साथ प्रत्येक वर्ग चार कोने वाले वर्गों को छोड़कर,परिमाप की एक इकाई के लिए जिम्मेदार है।वे परिमाप की दो इकाइयों के लिए जिम्मेदार हैं लेकिन क्षेत्रफल की केवल एक इकाई है।
प्रश्न:11.चतुर्भुज के परिमाप का सूत्र क्या होता है? (What is the formula for perimeter of a quadrilateral?):
उत्तर:सूत्र a+b+c+d=परिमाप है।उदाहरण के लिए,मान लीजिए कि एक चतुर्भुज की भुजाएँ 1, 5, 3 और 4 इंच लंबी हैं।परिमाप 1 + 5 + 3 + 4 या 13 इंच के बराबर होती है।
प्रश्न:12.परिमाप और क्षेत्रफल क्या है? (What is perimeter and area?):
उत्तर:परिमाप एक आकृति के बाहर की दूरी है अर्थात् किसी भी आकृति की सभी भुजाओं का योग परिमाप होती है।क्षेत्रफल किसी आकृति के अंदर के स्थान को मापता है।
प्रश्न:13.आप परिमाप और क्षेत्रफल का परिचय कैसे देते हैं? (How do you introduce perimeter and area?):
उत्तर:क्षेत्रफल और परिमाप सिखाने के लिए 8 रचनात्मक तरीके
एक क्षेत्रफल और परिमाप एंकर चार्ट बनाएं।एंकर चार्ट से शुरू करें!
अपनी कक्षा को सजाएं।
जब आप सीखते हैं तो नाश्ता करें (Snack while you learn)।
पैटर्न ब्लॉक बाहर खींचो (Pull out the pattern blocks)।
एक परिमाप व्यक्ति ड्रा करें (Draw a Perimeter Person)।
एक गणित मोज़ेक बनाओ (Make a math mosaic)।
लेगो ईंटों के साथ क्षेत्रफल और परिमाप का अन्वेषण करें (Explore area and perimeter with LEGO bricks)।
ब्लॉक लेटर नाम लिखें (Write block letter names)।
प्रश्न:14.क्या चतुर्भुज उत्तल है या अवतल? (Is a quadrilateral convex or concave?):
उत्तर:एक चतुर्भुज एक चार भुजाओं वाला बहुभुज है जिसे इसके गुणों के आधार पर कई श्रेणियों में वर्गीकृत किया जा सकता है।चतुर्भुज को उत्तल या अवतल के रूप में वर्गीकृत किया जा सकता है।यदि चतुर्भुज का अन्त: कोण 180 डिग्री से अधिक है,तो वह अवतल (concave) होता है।यदि चतुर्भुज का प्रत्येक अन्त:कोण 180° से कम हो तो वह उत्तल चतुर्भुज (convex) होता है।
प्रश्न:15.किस चतुर्भुज में समकोण नहीं है? (Which quadrilateral does not have right angles?):
उत्तर:समचतुर्भुज (rhombus)
एक समचतुर्भुज एक चतुर्भुज होता है जिसकी 4 बराबर भुजाएँ होती हैं।समान लंबाई की चार भुजाओं वाली एक आकृति।आकृति में समानांतर भुजाओं के दो सेट हैं और इनमें समकोण नहीं है।समान लंबाई की चार भुजाओं वाली एक आकृति।
प्रश्न:16.चतुर्भुज के 4 गुण क्या हैं? (What are the 4 properties of a quadrilateral?):
उत्तर:एक चतुर्भुज 4 भुजाओं वाला बंद आकार का होना चाहिए।एक चतुर्भुज के सभी अन्त: कोणों (internal angles) का योग 360° तक होता है
समचतुर्भुज (Rhombus):
विपरीत कोण बराबर होते हैं।
सभी भुजाएँ समान हैं और विपरीत भुजाएँ एक दूसरे के समानांतर हैं।
विकर्ण एक दूसरे को लंबवत समद्विभाजित करते हैं।
किन्हीं दो आसन्न कोणों (adjacent angles) का योग 180° होता है
प्रश्न:17.उत्तल चतुर्भुज का माप क्या है? (What is the measure of the convex quadrilateral?):
उत्तर:एक उत्तल चतुर्भुज के कोणों की मापों का योग 360° होता है क्योंकि उत्तल चतुर्भुज दो त्रिभुजों से बना होता है। हाँ,यह गुण एक चतुर्भुज के लिए भी सही है जो उत्तल नहीं है।ऐसा इसलिए है क्योंकि किसी भी चतुर्भुज को दो त्रिभुजों में विभाजित किया जा सकता है।
प्रश्न:18.अवतल चतुर्भुज की परिभाषा क्या है? (What is the definition of concave quadrilateral?):
उत्तर:एक अवतल चतुर्भुज के कोणों का योग 360° होता है।
अत: एक अवतल चतुर्भुज के सभी कोणों का अभीष्ट योग 360∘ है।नोट: किसी भी साधारण बहुभुज की तरह,एक अवतल बहुपद के आंतरिक कोणों का योग 180∘×(n−2) होता है,जहां n भुजाओं की संख्या होती है।
अवतल चतुर्भुज चार भुजा वाले बहुभुज होते हैं जिनका एक अन्त: कोण 180∘ से बड़ा होता है।हम अवतल चतुर्भुजों की पहचान इस तथ्य का उपयोग करके कर सकते हैं कि इसका एक विकर्ण आंशिक रूप से या पूरी तरह (partially or completely) से चतुर्भुज के बाहर स्थित है।
प्रश्न:19.उत्तल और अवतल चतुर्भुज की परिभाषा क्या है? (What is the definition of convex and concave quadrilateral?):
उत्तर:उत्तल चतुर्भुज: एक चतुर्भुज उत्तल चतुर्भुज कहलाता है,यदि चतुर्भुज के किन्हीं दो शीर्षों को मिलाने वाला रेखाखंड एक ही क्षेत्र (region) में हो।अवतल चतुर्भुज में कम से कम एक कोण प्रतिवर्त (वृहत कोण) कोण होता है,अर्थात 180° से बड़ा कोण।
प्रश्न:20.उत्तल चतुर्भुज कितने प्रकार के होते हैं? (How many types of convex quadrilateral are there?):
उत्तर:चतुर्भुज के प्रकार -आयत (Rectangle) ,वर्ग (Square),समचतुर्भुज (Rhombus),समांतर चतुर्भुज (Parallelogram)|
प्रश्न:21.चतुर्भुज से क्या तात्पर्य है? (What is meant by quadrilateral?):
उत्तर:एक चतुर्भुज एक चौकोर,आयत या समचतुर्भुज की तरह चार भुजाओं वाला बहुभुज होता है।अभी आप जिस कंप्यूटर स्क्रीन को देख रहे हैं, वह संभवत: एक चतुर्भुज के आकार की है।चतुर्भुज एक आकृति है जिसके बारे में आप ज्यामिति में सीखेंगे।जब आप चतुर्भुज शब्द देखते हैं, तो “चार भुजाएँ” सोचें।
प्रश्न:22.आयत एक उत्तल चतुर्भुज क्यों है? (Why rectangle is a convex quadrilateral?):
उत्तर:एक आयत एक उत्तल चतुर्भुज है क्योंकि इसका शीर्ष ऊपर उठा हुआ है और इसके दोनों विकर्ण इसके आंतरिक भाग में स्थित हैं।
प्रश्न:23.उत्तल चतुर्भुज से आप क्या समझते हैं? (What do you mean by convex quadrilateral?):
उत्तर:एक उत्तल चतुर्भुज एक चतुर्भुज है जिसमें सभी अन्त: कोण 180 डिग्री से कम होते हैं और सभी विकर्ण चतुर्भुज के भीतर स्थित होते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा चतुर्भुज का क्षेत्रफल (Area of Quadrilateral),निर्देशांक ज्यामिति में चतुर्भुज का क्षेत्रफल(Area of Quadrilateral Coordinate Geometry) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
