Baudhayan Theorem
1.बौधायन प्रमेय (Baudhayan Theorem),बौधायना प्रमेय (Baudhayana Theorem):
बौधायन प्रमेय (Baudhayan Theorem) से हमें समकोण त्रिभुज पर एक बहुत महत्त्वपूर्ण परिणाम प्राप्त होता है।यह प्रयेय पाइथागोरस प्रमेय(Pythagoras Theorem) के नाम से भी विख्यात है।
प्रमेय (Theorem):1.किसी समकोण त्रिभुज में कर्ण पर बना वर्ग अन्य दोनों भुजाओं पर बने वर्गों के योग के बराबर होता है।
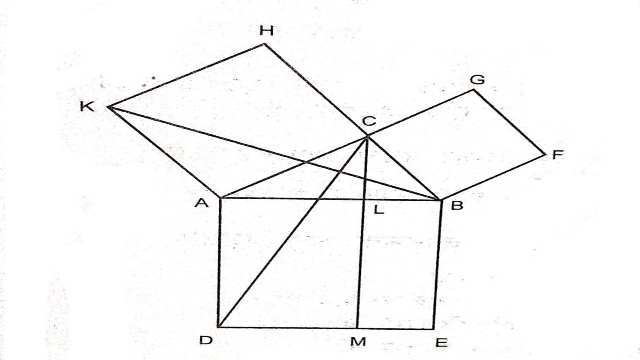
दिया है (Given):\triangle ABC में , \angle C समकोण है और भुजाओं AB,BC और CA पर बने वर्ग क्रमशः ADEB,CBFG और ACHK हैं।
सिद्ध करना है (To Prove):वर्ग ADEB=वर्ग ACHK+वर्ग CBFG
रचना (Construction):C से BE के समान्तर रेखा CM खींची जो AB को L पर प्रतिच्छेद करती है।BK एवं CD को मिलाया।
उपपत्ति (Proof):\angle BAD=\angle CAK=90^{\circ}
दोनों पक्षों में \angle CAB जोड़ने पर:
\angle BAD + \angle CAB=\angle CAK+\angle CAB \\ \Rightarrow \angle CAD=\angle BAK \cdots(1)
अब \triangle BAK और \triangle CAD में
AB=CD [वर्ग ABED की भुजाएं]
\angle BAK=\angle CAD[(1) से]
AK=AC [वर्ग ACHK की भुजाएं]
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle BAK \cong \triangle CAD \cdots(2)
पुनः \angle BCA=\angle ACH=90^{\circ} \\ \angle BCA+\angle ACH=180^{\circ}
अर्थात् BCH एक सरल रेखा है।
CH \parallel AK (वर्ग ACHK की सम्मुख भुजाएं)
\triangle BAK और वर्ग ACHK एक ही आधार AK तथा समान्तर रेखाओं AK एवं BH के मध्य स्थित हैं।
अतः \triangle BAK =\frac{1}{2} \text { वर्ग } ACHK \cdots(3)
इसी प्रकार \triangle ADC और आयत ADML एक ही आधार AD और समान्तर रेखाओं AD एवं CM के मध्य स्थित हैं,अतः
\triangle CAD =\frac{1}{2} \text { आयत } ADML \cdots(3)
समीकरण (2),(3) और (4) से:
\triangle CAD=\triangle BAK =\frac{1}{2} \text { वर्ग } ACHK \\=\frac{1}{2} \text { आयत } ADML
\therefore वर्ग ACHK=आयत ADML …….(5)
इसी प्रकार वर्ग CBFG=आयत LMEB ……..(6)
(5) और (6) से:
आयत ADML+आयत LMEB=वर्ग ACHK+वर्ग CBFG
वर्ग ADEB=वर्ग ACHK+वर्ग CBFG
प्रमेय (Theorem):2.(बौधायन प्रमेय का विलोम) (Converse of Baudhayan Theorem):
किसी त्रिभुज में यदि एक भुजा का वर्ग अन्य दोनों भुजाओं के वर्गों के योग के बराबर हो तो इस भुजा के सामने का कोण समकोण होता है।
दिया है (Given):\triangle ABC में,AB^{2}+BC^{2}=AC^{2}
सिद्ध करना है (To Prove):\angle B=90^{\circ}
रचना (Construction):\triangle PQR इस प्रकार बनाया कि \angle Q=90^{\circ} हों और PQ=AB एवं QR=BC हों।
उपपत्ति (Proof): \triangle PQR में बौधायन प्रमेय (Baudhayan Theorem) से
PR^{2}=PQ^{2}+QR^{2}
परन्तु PQ=AB और QR=BC
अतः PR^{2}=AB^{2}+BC^{2} \cdots(1)
दिया हुआ है कि
AC^{2}=AB^{2}+BC^{2}
समीकरण (1) और (2) से:
PR=AC
अब \triangle ABC एवं \triangle PQR में
PQ=AB (रचना से)
QR=BC (रचना से)
PR=AC [(3) से]
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle ABC \cong \triangle PQR अतः \angle B=\angle Q=90^{\circ}
अर्थात् \angle B=90^{\circ}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Theorem of Area of Parallelogram
2.बौधायन प्रमेय के उदाहरण (Baudhayan Theorem Examples):
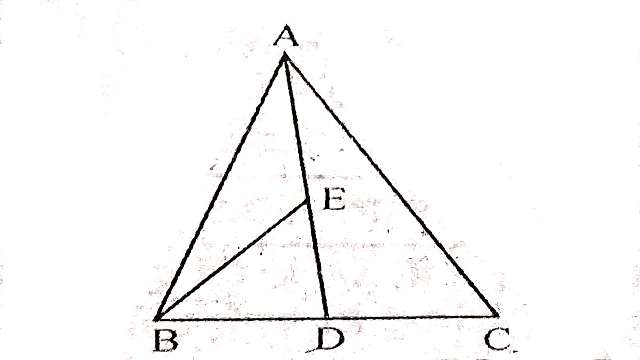
Example:1.\triangle ABC में,E माध्यिका AD का मध्य-बिन्दु है।दर्शाइए कि ar ( BED)=\frac{1}{4} ar(ABC)
Solution:दिया है (Given):\triangle ABC में,E माध्यिका AD का मध्य-बिन्दु है।
सिद्ध करना है (To Prove): ar( BED)=\frac{1}{4} ar(ABC)
उपपत्ति :-\triangle ABC में चूंकि AD माध्यिका है
ar(\triangle ABD)=ar(\triangle ACD)=\frac{1}{2} ar(\triangle ABC) \cdots(1)
(\because त्रिभुज की माध्यिका त्रिभुज को बराबर क्षेत्रफल वाले दो त्रिभजों में विभाजित करतीं है)
\triangle ABD में चूंकि BE एक माध्यिका है।
ar(\triangle BED)=ar(\triangle BEA)=\frac{1}{2} ar(\triangle ABD) \cdots(2)
(\because त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है)
समीकरण (1) से:
ar(\triangle BED)=\frac{1}{2} ar(\triangle ABD) \\ =\frac{1}{2} .\frac{1}{2} ar(\triangle ABC) \\ \Rightarrow ar(\triangle BED)=\frac{1}{4} ar(\triangle ABC)
Example:2.चित्र में ABCD और EFGD दो समान्तर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिन्दु है।तब ar(DPC)=ar(EFGD) है।
Solution:दिया है (Given):ABCD और EFGD दो समान्तर चतुर्भुज है तथा G भुजा CD का मध्य-बिन्दु है।
उपपत्ति (Proof):\triangle DPC तथा समान्तर चतुर्भुज एक ही आधार DC तथा समान भुजाओ AB व CD के मध्य स्थित है
अतः ar(\triangle DPC)=\frac{1}{2} ar(ABCD) \cdots(1)
समान्तर चतुर्भुज ABCD और EFGD का आधार क्रमशः DC व DG है जहाँ G,DC का मध्य-बिन्दु है तथा दोनों समान समान्तर भुजाओं के मध्य स्थित हैं अतः
ar(\triangle EFGD)=\frac{1}{2} ar(ABCD) \cdots(2)
(1) व (2) से:
ar(\triangle DPC)=ar( EFGD)
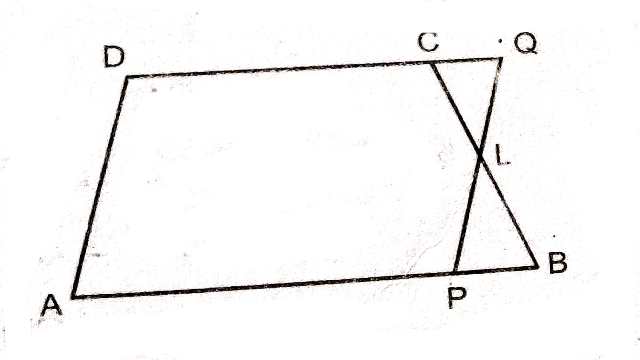
Example:3.एक समलम्ब चतुर्भुज ABCD में AB \parallel DC तथा L भुजा BC का मध्य-बिन्दु है।L से होकर एक रेखा खींची PQ \parallel AD गई है जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है।सिद्ध कीजिए कि ar(ABCD)=ar(APQD)
Solution:दिया है (Given):समलम्ब चतुर्भुज ABCD में AB \parallel DC तथा PQ \parallel AD है।साथ ही PL=QL है।
सिद्ध करना है (To Prove):ar(ABCD)=ar(APQD)
उपपत्ति (Proof):\triangle PBL तथा \triangle QCL में
PL=QL (दिया है)
\angle BPL=\angle CQL(एकान्तर कोण)
\angle BLP=\angle CLQ(शीर्षाभिमुख कोण)
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Congruence property)
\triangle PBL \cong \triangle QCL \\ ar(\triangle PBL)=ar(\triangle CQL) \cdots(1)
(सर्वांगसम त्रिभुजों के क्षेत्रफल समान होते हैं)
ar(ABLQDA)=ar(ABLQDA) …….(2)
(2) में से (1) घटाने पर:
ar(ABLQDA)-ar(\triangle PBL)=ar(ABLQDA)-ar(\triangle CQL) \\ \Rightarrow ar(APQD)=ar(ABCD)
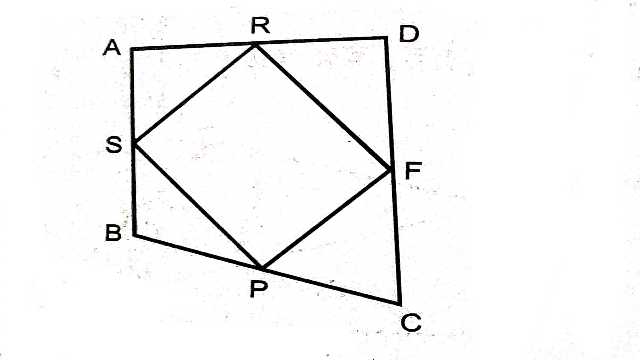
Example:4.यदि किसी चतुर्भुज की भुजाओं के मध्य बिन्दुओं को क्रम से मिलाया जाता है तो सिद्ध कीजिए कि इस प्रकार बने समान्तर चतुर्भुज का क्षेत्रफल दिए हुए चतुर्भुज के क्षेत्रफल का आधा होता है।
Solution:दिया है (Given):चतुर्भुज ABCD की भुजाओं के मध्य बिन्दुओं को मिलाने पर समान्तर चतुर्भुज PFRS है।
सिद्ध करना है (To Prove):\frac{1}{2} ar(ABCD)=ar(PFRS)
रचना (Construction):BD को मिलाया तथा BD पर लम्ब AL खींचा।
उपपत्ति (Proof):\triangle ABD में S व R मध्य-बिन्दु है अतः
SR \parallel BD, SR=\frac{1}{2} BD तथा ML=\frac{1}{2} AL \cdots(1)
\triangle ABD \text{ का क्षेत्रफल }=\frac{1}{2} \times \text{ आधार } \times \text{ ऊँचाई } \\ ar(\triangle ABD) =\frac{1}{2} \times BD \times AL \cdots(2)
समान्तर चतुर्भुज STUR का क्षेत्रफल=आधार × ऊँचाई
=TU × ML
=\frac{1}{2} BD \times \frac{1}{2} AL[(1) से]
ar(STUR)=\frac{1}{4} BD \times AL
(1) व (2) से:
\frac{1}{2} ar(\triangle ABD)=ar(STUR) \cdots(4)
इसी प्रकार \frac{1}{2} ar(\triangle PCF)=ar(PFUT) \cdots(5)
(4) व (5) को जोड़ने पर:
\frac{1}{2} ar(\triangle ABD)+ \frac{1}{2} ar(\triangle PCF)=ar(STUR)+ar(PFUT) \\ \Rightarrow \frac{1}{2} ar(ABCD)=ar(PFRS)
Example:5.एक समबाहु त्रिभुज \triangle ABC में,AD भुजा BC पर लम्बवत हो तो सिद्ध कीजिए कि 3AB^{2}=4 AD^{2}
Solution:दिया है (Given):\triangle ABC समबाहु त्रिभुज है अर्थात् AB=BC=AC तथा AD \perp BC है।
सिद्ध करना है (To Prove):3AB^{2}=4 AD^{2}
उपपत्ति (Proof):समकोण \triangle ABD में
AB^{2}=AD^{2}+BD^{2}(बौधायन प्रमेय से)
\Rightarrow AB^{2}=AD^{2}+\left ( \frac{AB}{2} \right )^{2}(BD=DC)
[समबाहु त्रिभुज का शीर्षलम्ब सम्मुख भुजा को समद्विभाजित करता है)
\Rightarrow AB^{2}=AD^{2}+\frac{AB^{2}}{4} \\ \Rightarrow AB^{2}-\frac{AB^{2}}{4}=AD^{2} \\ \Rightarrow \frac{4 AB^{2}-AB^{2}}{4}=AD^{2} \\ \Rightarrow \frac{3 AB^{2}}{4}=AD^{2} \\ \Rightarrow 3 AB^{2}=4 AD^{2}
Example:6.एक अधिककोण \triangle ABC में कोण C अधिक कोण हैं।AD \perp BC है और BC को आगे बढ़ाने पर D पर मिलता है।सिद्ध कीजिए कि AB^{2}=AC^{2}+BC^{2}+2 BC \cdot CD
Solution:दिया है (Given): \triangle ABC अधिक कोण त्रिभुज है तथा है।
सिद्ध करना है (To Prove):AB^{2}=AC^{2}+BC^{2}+2 BC \cdot CD
उपपत्ति (Proof):\triangle ADB एक समकोण त्रिभुज है जिसका कोण D समकोण है।अतः
AB^{2}=AD^{2}+DB^{2} (By Baudhayan Theorem)
=AD^{2}+(DC+BC)^{2} \\ AB^{2}=AD^{2}+DC^{2}+BC^{2}+2BC \cdot CD \cdots(1)
समकोण \triangle ADB में
AC^{2}=AD^{2}+DC^{2}(By Baudhayan Theorem)….(2)
(1) व (2) से:
AB^{2}=AC^{2}+BC^{2}+2 BC \cdot CD
Example:7.आयत ABCD के अन्दर कोई बिन्दु O है।सिद्ध कीजिए कि OB^{2}+OD^{2}=OA^{2}+OC^{2}
Solution:दिया है (Given):O एक बिन्दु आयत ABCD के अन्तर्गत है।
सिद्ध करना है (To Prove):OB^{2}+OD^{2}=OA^{2}+OC^{2}
रचना (Construction):PQ \parallel BC खींचा।
उपपत्ति (Proof):ABCD एक आयत है।
\angle B=\angle C=90^{\circ}
AD \parallel BC तथा AB \parallel DC
PQ \parallel BC (रचना से)
PQ \parallel AD \parallel BC
BC \perp AB और BC \parallel PQ \\ PQ \perp AB
इसी प्रकार PQ \perp DC \\ \angle APO=\angle BPO =\angle CQO=\angle DQO=90^{\circ}
APQD और BPQL एक आयत है।
AP=DQ और BP=CQ
समकोण \triangle BPO में OB^{2}=OP^{2}+BP^{2}(By Baudhayan Theorem)
OB^{2}=OP^{2}+CQ^{2} (\because BP=CQ) \cdots(1)
समकोण \triangle DQO में OD^{2}=OQ^{2}+DQ^{2} (By Baudhayan Theorem)
OD^{2}=OQ^{2}+AP^{2} (\because DQ=AP) \cdots(2)
समकोण \triangle APO में OA^{2}=OP^{2}+AP^{2}(By Baudhayan Theorem) ….(3)
समकोण \triangle CQO में OC^{2}=OQ^{2}+CQ^{2} (By Baudhayan Theorem)….(4)
(1) और (2) को जोड़ने पर:
OB^{2}+OD^{2}=OP^{2}+CQ^{2}+OQ^{2}+AP^{2} \\ =(OP^{2}+AP^{2})+(CQ^{2}+OQ^{2}) \\ \Rightarrow OB^{2}+OD^{2}=OA^{2}+OC^{2}[(3) और (4) से ]
उपर्युक्त उदाहरणों के द्वारा बौधायन प्रमेय (Baudhayan Theorem),बौधायना प्रमेय (Baudhayana Theorem) को समझ सकते है।
3.बौधायन प्रमेय की समस्याएं (Baudhayan Theorem Problems):
(1.) एक व्यक्ति 10 मीटर पूर्व की ओर जाता है और तब 30 मीटर उत्तर की ओर जाता है।उसकी प्रारंभिक स्थान से दूरी ज्ञात कीजिए।
(2.)एक सीढ़ी दीवार के साथ इस प्रकार रखी हुई है कि इसका नीचे का सिरा दीवार से 7 मीटर दूर है।यदि इसका दूसरा सिरा 24 मीटर ऊंची एक खिड़की तक पहुंचे तो सीढ़ी की लंबाई ज्ञात कीजिए।
(3.)एक समबाहु त्रिभुज के शीर्षलम्ब और क्षेत्रफल ज्ञात कीजिए जिसकी भुजा की लंबाई a है।
(4.)एक वर्ग के विकर्ण की लंबाई ज्ञात कीजिए जिसकी प्रत्येक भुजा 4 मीटर है।
उत्तर( (Answers):(1) 10 \sqrt{10} \text { मीटर } \\ (2.)25 \text { मीटर } \\ (3)\frac{\sqrt{3}}{2} a ,\frac{\sqrt{3}}{4} a^{2} \\ (4) 4 \sqrt{2}
उपर्युक्त सवालों को हल करने पर बौधायन प्रमेय (Baudhayan Theorem),बौधायना प्रमेय (Baudhayana Theorem) को ठीक से समझ सकते हैं।
Also Read This Article:-Angles of a Triangle
4.बौधायन प्रमेय (Baudhayan Theorem),बौधायना प्रमेय (Baudhayana Theorem) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.पाइथागोरस प्रमेय के लिए प्रयुक्त सूत्र क्या है? (What is the formula used for the Pythagorean Theorem?):
उत्तर:पाइथागोरस प्रमेय का विलोम एक नियम है जिसका उपयोग त्रिभुजों को समकोण त्रिभुज,न्यूनकोण त्रिभुज या अधिक कोण त्रिभुज के रूप में वर्गीकृत करने के लिए किया जाता है।पाइथागोरस प्रमेय को देखते हुए,a^{2} + b^{2}= c^{2},तब: एक न्यून त्रिभुज के लिए, c^{2}< a^{2} + b^{2}, जहां c न्यून कोण के विपरीत भुजा है।
बौधायन सुल्व सूत्र (1000 ईसा पूर्व) को आज पाइथोगोरस प्रमेय के रूप में जाना जाता है, जिसमें कहा गया है कि एक समकोण त्रिभुज में, कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है।
प्रश्न:2.बौधायन का जन्म कब हुआ था? (When was Baudhayana born?):
उत्तर:माना जाता है कि बौधायन का जन्म लगभग 800 ईसा पूर्व हुआ था जबकि पाइथागोरस का जन्म 570 ईसा पूर्व में हुआ था।पाइथागोरस के नाम से प्रचलित लोकप्रिय प्रमेय का कहना है कि कर्ण की लंबाई का वर्ग समकोण त्रिभुज में दो अन्य भुजाओं के वर्गों के योग के बराबर होता है।
प्रश्न:3.बौधायन प्रमेय का आविष्कार किसने किया? (Who invented Baudhayana Theorem?):
उत्तर:पाइथागोरस
प्रमेय का उल्लेख भारत के बौधायन सुलब-सूत्र में मिलता है,जो 800 और 400 ईसा पूर्व के बीच लिखा गया था।फिर भी इस प्रमेय के लिए पाइथागोरस को श्रेय दिया जाने लगा।वास्तविक रूप में जो पाइथागोरस के नाम से प्रमेय प्रसिद्ध है,उसको सबसे पहले बौधायन ने खोज लिया था जिसका उल्लेख बौधायन शुल्व सूत्र में मिलता है।
प्रश्न:4.आप A^{2}+B^{2} =C^{2} को कैसे हल करते हैं? (How do you solve A^{2}+B^{2} =C^{2}?):
उत्तर:सूत्र A^{2}+B^{2} =C^{2} है,यह उतना ही सरल है जितना कि त्रिभुज की एक भुजा का वर्ग और त्रिभुज की दूसरी भुजा का वर्ग,त्रिभुज के कर्ण के वर्ग के बराबर होता है।यह नियम केवल समकोण त्रिभुज के लिए लागू होता है।
प्रश्न:5.गौगु प्रमेय क्या है? (What is Gougu Theorem?):
उत्तर:गौगु प्रमेय यह है कि “समकोण त्रिभुज में,दो दाहिनी भुजाओं के वर्गों का योग कर्ण के वर्ग के बराबर होता है।” दूसरे शब्दों में,समकोण त्रिभुज की तीन भुजाएँ (a, b, c) निम्नलिखित समीकरण को संतुष्ट करती हैं: a^{2}+b^{2} =c^{2} जहाँ a को Gou कहा जाता है,b Gu है और c Xian है।
प्रश्न:6.बौधायन ने क्या लिखा था? (What was written by Baudhayana?):
उत्तर:निस्संदेह उन्होंने धार्मिक संस्कारों के लिए नियम प्रदान करने के लिए सुल्बसूत्र लिखा था और यह लगभग निश्चित प्रतीत होगा कि बौधायन स्वयं एक वैदिक पुजारी होंगे।सुल्बसूत्रों में दिया गया गणित बलिदान के लिए आवश्यक वेदियों के सटीक निर्माण को सक्षम करने के लिए है।
हमारे विचार से बौधायन मात्र एक वैदिक पुजारी नहीं थे बल्कि एक ऋषि थे वरना आज भी लाखों की संख्या में मन्दिरों में पुजारी हैं वे कौनसी गणित अथवा ज्योतिष का विकास तथा आविष्कार करते हैं।वैदिक ऋषि ऋतम्भरा प्रज्ञा के द्वारा ऐसी ऋचाओं का निर्माण करते थे।
प्रश्न:7.विश्व का प्रथम गणितज्ञ कौन है ? (Who is the first mathematician in world?):
उत्तर:मिलेटस के थेल्स (Thales of Miletus)
सबसे पहले ज्ञात गणितज्ञों में से एक थेल्स ऑफ मिलेटस थे (c.624-c.546 ईसा पूर्व);उन्हें पहले सच्चे गणितज्ञ और पहले ज्ञात व्यक्ति के रूप में सम्मानित किया गया है, जिनके लिए गणितीय खोज का श्रेय दिया गया है।
प्रश्न:8.आधुनिक गणित के जनक कौन है ? (Who is the father of modern mathematics?):
उत्तर:रेने डेस्कर्टेस (Rene Descartes)
रेने डेसकार्टेस (Rene Descartes) (31 मार्च,1596-11 फरवरी,1650),जिसे कार्टेसियस (Cartesius) के नाम से भी जाना जाता है,एक प्रसिद्ध फ्रांसीसी दार्शनिक,गणितज्ञ और वैज्ञानिक थे।”आधुनिक दर्शन के संस्थापक”और “आधुनिक गणित के पिता” के रूप में डब किया गया,वह आधुनिक समय के सबसे महत्वपूर्ण और प्रभावशाली विचारकों में से एक के रूप में रैंक करता है।
प्रश्न:9.विश्व का सर्वश्रेष्ठ गणितज्ञ कौन है? (Who is world best mathematician?):
उत्तर:10 बेहतरीन गणितज्ञ
Hypatia (cAD 360-415) Hypatia (375-415AD), एक यूनानी महिला गणितज्ञ और दार्शनिक।
गिरोलामो कार्डानो (Girolamo Cardano)(1501-1576)
लियोनहार्ड यूलर (Leonhard Euler) (1707-1783)
कार्ल फ्रेडरिक गॉस (Carl Friedrich Gauss) (1777-1855)
जॉर्ज कैंटर (Georg Cantor) (1845-1918)
पॉल एर्डोस (Paul Erdös) (1913-1996)
जॉन हॉर्टन कॉनवे (John Horton Conway) (b1937)
ग्रिगोरी पेरेलमैन (Grigori Perelman) (b1966)
प्रश्न:11.बीजगणित के जनक कौन है ? (Who is the father of algebra?):
उत्तर:अल-ख्वारिज्मी (Al-Khwarizmi)
अल-ख्वारिज्मी (Al-Khwarizmi): बीजगणित के पिता।
प्रश्न:12.3 महान गणितज्ञ कौन हैं? (Who are the 3 greatest mathematicians?):
उत्तर:सर्वश्रेष्ठ 8 गणितज्ञ हैं:
लियोनहार्ड यूलर (Leonhard Euler)।
श्रीनिवास रामानुजन (Srinivasa Ramanujan)
कार्ल फ्रेडरिक गॉस (Carl Friedrich Gauss)।
आइजैक न्यूटन (Isaac Newton)।
यूक्लिड (Euclid)।
आर्किमिडीज (Archimedes)।
आर्यभट (Aryabhatta)।
गॉटफ्राइड डब्ल्यू (Gottfried W.)।
प्रश्न:13.क्या गणितज्ञ सबसे चतुर लोग हैं? (Are mathematicians the smartest people?):
उत्तर:नहीं,गणितज्ञ और सैद्धांतिक भौतिक विज्ञानी दुनिया के सबसे बुद्धिमान लोग नहीं हैं।शायद वे हैं यदि हम केवल तार्किक-गणितीय बुद्धि (logical-mathematical intelligence) पर विचार करते हैं,लेकिन कई अन्य पहलू हैं जिन पर विचार करने की आवश्यकता है।मल्टीपल इंटेलिजेंस (Multiple Intelligence) एंड इंटेलिजेंस फैक्टर (जी फैक्टर) [Intelligence factor (g factor)] नामक एक अवधारणा है।
प्रश्न:14.समान चिन्ह का आविष्कार किसने किया? (Who invented equal sign?):
उत्तर:रॉबर्ट रिकॉर्डे (Robert Recorde)
उत्तर:गणित के VNR Concise Encyclopedia के अनुसार,इंग्लैंड के राजा एडवर्ड VI (England’s King Edward VI) और क्वीन मैरी (Queen Mary) के रॉयल कोर्ट फिजिशियन रॉबर्ट रिकॉर्डे (Robert Recorde) द्वारा समान चिह्न का आविष्कार किया गया था।
प्रश्न:15.टेरेंस ताओ आईक्यू क्या है? (What is Terence Tao IQ?):
उत्तर:230 के उत्कृष्ट आईक्यू के साथ,टेरेंस ताओ (Terence Tao) का जन्म 17 जुलाई,1975 को ऑस्ट्रेलिया (Australia) के एडिलेड (Adelaide) में हुआ था।
प्रश्न:16.ग्रिगोरी पेरेलमैन आईक्यू क्या है? (What is Grigori Perelman IQ?):
उत्तर:ग्रिगोरी पेरेलमैन (Grigori Perelman) एक रूसी गणितज्ञ हैं जिन्होंने गणित में सबसे कठिन समस्याओं में से एक के प्रमाण के लिए $1M और नोबेल पुरस्कार (फील्ड्स मेडल) [Nobel Prize (Fields Medal)] के बराबर से लेने से.इनकार कर दिया।2019 के एक अध्ययन के आधार पर,ग्रिगोरी पेरेलमैन (Grigori Perelman) का आईक्यू 172 है।
प्रश्न:17.गणित में ≡ का क्या अर्थ होता है? (What does ≡ mean in math?):
उत्तर:≡ का अर्थ के समान
≡ का अर्थ समान है (means identical to)।यह समान है,लेकिन बिल्कुल बराबर नहीं है।इसलिए,यदि संदेह है,तो = पर टिके रहें।≈ का अर्थ है लगभग बराबर (approximately equal to) या लगभग बराबर (almost equal to)।
प्रश्न:18.समान चिन्ह किसे कहते हैं? (What is an equal sign called?):
उत्तर:बराबर चिह्न (equals sign) (ब्रिटिश अंग्रेजी,यूनिकोड कंसोर्टियम)[(British English, Unicode Consortium)] या बराबर चिह्न (equality sign) (अमेरिकी अंग्रेजी),जिसे पहले समानता चिह्न (equality sign) के रूप में जाना जाता था,गणितीय प्रतीक=है,जिसका उपयोग कुछ अच्छी तरह से परिभाषित अर्थों में समानता को इंगित करने के लिए किया जाता है।
प्रश्न:19.ग्रिगोरी पेरेलमैन अब क्या कर रहा है? (What is Grigori Perelman doing now?):
उत्तर:पेरेलमैन अपनी मां के साथ सेंट पीटर्सबर्ग (St. Petersburg) उपनगर में एक स्पार्टन अपार्टमेंट (spartan apartment) में रहता है।वह एक वायलिन बजाता है।केवल उनकी फैशन शैली इस तथ्य को धोखा देती है कि उन्होंने एक व्याख्याता के रूप में पश्चिमी विश्वविद्यालय परिसरों में समय बिताया।
प्रश्न:20.ग्रिगोरी पेरेलमैन कितनी आयु है? (How old is Grigori Perelman?):
ग्रिगोरी पेरेलमैन (Grigori Perelman)/ आयु
प्रश्न:21.क्या पेरेलमैन प्रतिभाशाली है? (Is Perelman genius?):
उत्तर:जब रूसी गणितज्ञ ग्रिगोरी ‘ग्रिशा’ पेरेलमैन (Russian mathematician Grigory ‘Grisha’ Perelman) ने अपना समाधान इंटरनेट पर पोस्ट किया,तो लोगों ने नोटिस लिया। सेंट पीटर्सबर्ग (St Petersburg)(उस समय लेनिनग्राद,Leningrad) में जन्मे,पेरेलमैन गणित के कौतुक बन गए।16 साल की उम्र में उन्होंने 1982 के अंतर्राष्ट्रीय गणितीय ओलंपियाड में एक पूर्ण स्कोर के साथ स्वर्ण पदक जीता।
प्रश्न:22.रीमैन की परिकल्पना का समाधान किसने किया? (Who Solved Riemann hypothesis?):
उत्तर:सर माइकल अतियाहो (Sir Michael Atiyah)
रीमैन परिकल्पना सात गणित की समस्याओं में से एक है जो आपको क्ले गणित संस्थान से $1 मिलियन जीत सकती है यदि आप इसे हल कर सकते हैं।ब्रिटिश गणितज्ञ सर माइकल अतिया (Sir Michael Atiyah) ने सोमवार को दावा किया कि उन्होंने 160 साल पुरानी समस्या को हल कर दिया है।अतियाह पहले ही अपने करियर में फील्ड्स मेडल (Fields Medal) और एबेल पुरस्कार (Abel Prize) जीत चुके हैं।
प्रश्न:23.पोंकारे अनुमान का समाधान किसने किया? (Who solved the Poincaré conjecture?):
उत्तर:ग्रिगोरी “ग्रिशा” पेरेलमैन (Grigori “Grisha” Perelman)
रूसी गणितज्ञ ग्रिगोरी “ग्रिशा” पेरेलमैन (Grigori “Grisha” Perelman) को पिछले साल 18 मार्च को समस्याओं में से एक,पोंकारे अनुमान (Poincaré conjecture) को हल करने के लिए पुरस्कार से सम्मानित किया गया था-अभी तक केवल एक ही हल किया गया है।पारिवारिक रूप से, उन्होंने $ 1,000,000 मिलेनियम ($1,000,000 Millennium Prize) पुरस्कार को ठुकरा दिया।
प्रश्न:24.मिलेनियम समस्या का समाधान किसने किया? (Who solved the millennium problem?):
उत्तर:ग्रिगोरी पेरेलमैन (Grigori Perelman)
रूसी गणितज्ञ ग्रिगोरी पेरेलमैन ने कई साल पहले दुनिया की सबसे जटिल गणित की समस्याओं में से एक को हल किया था।पॉइनकेयर अनुमान (Poincare Conjecture) सात मिलेनियम पुरस्कार समस्याओं में से पहला था जिसे हल किया जाना था।
प्रश्न:25.फ़र्मेट के अंतिम प्रमेय को किसने हल किया? (Who solved Fermat’s Last Theorem?):
उत्तर:एंड्रयू विल्स (Andrew Wiles)
संख्या सिद्धांत (number theory) में तीन सदी पुरानी समस्या को हल करने के लिए गणितज्ञ को प्रतिष्ठित पुरस्कार मिला।ब्रिटिश संख्या सिद्धांतकार एंड्रयू विल्स (Andrew Wiles) को फ़र्मेट के अंतिम प्रमेय (Fermat’s last theorem) के समाधान के लिए 2016 का एबेल पुरस्कार (Abel Prize) मिला है-एक ऐसी समस्या जिसने साढ़े तीन शताब्दियों तक दुनिया के कुछ महानतम दिमागों को स्तब्ध कर दिया।
उपर्युक्त प्रश्नों के उत्तर द्वारा बौधायन प्रमेय (Baudhayan Theorem),बौधायना प्रमेय (Baudhayana Theorem) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |