Trigonometry
1.त्रिकोणमिति (Trigonometry):
- त्रिकोणमिति (Trigonometry) या त्रिभुज मापन ज्यामिति की एक महत्त्वपूर्ण शाखा है।त्रिभुजों के कुछ कोण या भुजाएं ज्ञात होने पर शेष कोणों और भुजाओं का मान हम त्रिकोणमिति की सर्वसमिकाओं तथा न्यून कोणों के त्रिकोणमितीय अनुपातों द्वारा निकाल सकते हैं।इस तरह हम बहुत प्रकार के सवालों के हल ज्ञात कर सकते हैं।
- आर्यभट ने अपनी पुस्तक आर्यभटीय में त्रिकोणमिति के बारे में कुछ विशेष बातें बताई गई हैं।त्रिकोण की तीन भुजाओं और तीन कोणों के संबंधों के बारे में जो गणित रचा जाता है उसे त्रिकोणमिति कहते हैं।ज्योतिषशास्त्र में त्रिकोणमिति की बड़ी जरूरत होती है।आर्यभट ने त्रिकोणमिति में एक नई पद्धति का आविष्कार किया था।इस नई पद्धति को ज्या या भुजज्या की पद्धति कहते हैं।आजकल स्कूल-कॉलेजों में जो त्रिकोणमिति पढ़ाई जाती है वह आर्यभट की इसी पद्धति पर आधारित है।यूनान के गणितज्ञों को इस पद्धति का ज्ञान नहीं था।यह भारतीय आविष्कार पहले अरब देशों में पहुंचा और उसके बाद यूरोप में इसका प्रचार हुआ।
- आर्यभट की इस पद्धति का प्रचार विदेशों में कैसे हुआ,यह एक शब्द पर विचार करने से मालूम हो जाएगा।एक शब्द की मजेदार कहानी है।समकोण त्रिभुज की दो भुजाओं के अनुपात के लिए अंग्रेजी का एक शब्द है:’साईन’।आज से डेढ़ हजार साल पहले हमारे देश में इसी के लिए शब्द था ज्या या जीवा।यकीन करना कठिन है पर अंग्रेजी का यह ‘साइन’ शब्द ‘जीवा’ शब्द से ही बना है।आठवीं-नवीं शताब्दी में अरबी विद्वान गणित और ज्योतिष के भारतीय ग्रंथों का अरबी भाषा में अनुवाद कर रहे थे।उनके सामने संस्कृत का यह ‘जीवा’ शब्द आया तो वे चक्कर में पड़ गए।इस शब्द का अरबी में अनुवाद न करके उन्होंने इसे ज्यों का त्यों अपना लिया।अरबी लिपि में स्वरों के लिए अक्षर नहीं होते इसलिए इस ‘जीवा’ शब्द को उन्होंने ‘ज-ब’ के रूप में लिखा।
- 11वीं शताब्दी में अरबी ग्रंथों के यूरोप की लैटिन भाषा में अनुवाद होने लगे थे।यूरोप के पंडितों के सामने यह ‘ज-ब’ शब्द आया तो वे भी भौचक्के रह गए।वे नहीं जानते थे कि यह मूलतः भारत की संस्कृत भाषा का शब्द है।उन्होंने गलती से इसे अरबी भाषा का ‘जेब’ शब्द मान लिया जिसका अर्थ होता है ‘खीसा’ या ‘छाती’।इसलिए अनुवाद करते समय उन्होंने इसके लिए लैटिन का शब्द चुना ‘सिनुस्’ जिसका अर्थ होता है ‘छाती’।कहां संस्कृत का ‘जीवा’ शब्द और कहाँ छाती के अर्थवाला लैटिन का यह ‘सिनुस’ शब्द।इसी तरह ‘सिनुस’ शब्द से आज की अंग्रेजी का ‘साइन’ शब्द बना है।पर अंग्रेजी के माध्यम से त्रिकोणमिति पढ़नेवाले आज के कितने विद्यार्थी जानते हैं कि यह ‘साइन’ शब्द और त्रिकोणमिति की आधुनिक विधि मूलत: भारतीय आविष्कार है?
- इसके तुरंत बाद ‘sine’ के रूप में प्रयुक्त शब्द ‘sinus’ भी पूरे यूरोप में गणितीय पाठों में प्रयुक्त होने लगा।खगोलविद् के एक अंग्रेजी प्रोफेसर एडमंड गुंटर (1581-1626) ने पहले-पहल संक्षिप्त संकेत ‘sin’ का प्रयोग किया था।
शब्दों ‘cosine’ और ‘tangent’ का उद्गम बहुत बाद में हुआ था।cosine फलन का उद्गम पूरक कोण के sine का अभिकलन करने को ध्यान में रखकर किया गया था।आर्यभट ने इसे कोटिज्या का नाम दिया था।नाम cosinus का उद्गम एडमंड गुंटर के साथ हुआ था।1674 में अंग्रेज गणितज्ञ सर जोनास मूरे ने पहले-पहल संक्षिप्त संकेत ‘cos’ का प्रयोग किया था। - भारतीय ज्योतिष और गणित के कई आविष्कार पहले अरब देशों में पहुंचे और तदन्तर यूरोप के देशों में उनका प्रचार हुआ था।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Height and Distance in Trigonometry
(1.)त्रिकोणमिति की व्युत्पत्ति (Etymology of Trigonometry):
- उपर्युक्त विवरण से स्पष्ट है कि गणित की इस शाखा त्रिकोणमिति में सभी स्थितियों में दूरियां और ऊंचाइयां कुछ गणितीय तकनीकों को लागू करके ज्ञात किया जा सकता है।अंग्रेजी शब्द ‘trigonometry’ की व्युत्पत्ति ग्रीक शब्दों ‘tri’ (जिसका अर्थ है तीन),’gon’ (जिसका अर्थ है भुजा) और ‘metron’ (जिस अर्थ है माप) से हुई है।
- वस्तुत: त्रिकोणमिति में एक त्रिभुज की भुजाओं और कोणों के बीच के संबंधों का अध्ययन किया जाता है।प्राचीन काल में त्रिकोणमिति पर किए गए कार्य का उल्लेख मिस्र और बेबीलोन (वर्तमान इराक) में भी मिलता है।प्राचीनकाल के खगोलविद् त्रिकोणमिति का प्रयोग पृथ्वी से तारों और ग्रहों की दूरियां मापने में करते थे।आज भी इंजीनियरिंग और भौतिक विज्ञान में प्रयुक्त अधिकांश प्रौद्योगिकीय उन्नत विधियाँ त्रिकोणमितीय संकल्पनाओं पर आधारित है।
(2.)त्रिकोणमिति के अनुप्रयोग (Applications of Trigonometry):
- उपर्युक्त विवरण से स्पष्ट है कि त्रिकोणमिति एक प्राचीनतम विषय है जिसका अध्ययन सर्वप्रथम भारत से होते हुए पूरे जगत के विद्वान करने लगे हैं। त्रिकोणमिति का आविष्कार इस बात को ध्यान में रखकर किया गया था कि इसकी खगोलिकी में आवश्यकता पड़ती थी।तब से आज तक खगोलविद् इसका प्रयोग पृथ्वी से ग्रहों और तारों की दूरियां की गणना करने में करते आए हैं। त्रिकोणमिति का प्रयोग भूगोल और नौचालन में भी किया जाता है।त्रिकोणमिति के ज्ञान का प्रयोग मानचित्र बनाने और देशांतर (longitude) और अक्षांश (latitude) के सापेक्ष एक द्वीप की स्थिति ज्ञात करने में भी की जाती है।
- सर्वेक्षक शताब्दियों से त्रिकोणमिति का प्रयोग करते आ रहे हैं।19वीं शताब्दी की ‘बृहत् त्रिकोणमितीय सर्वेक्षण’ ब्रितानी भारत की एक ऐसी विशाल सर्वेक्षण परियोजना थी जिसके लिए दो बृहत्तम थियोडोलाइट (Theodolite) का निर्माण किया गया था।1852 में सर्वेक्षण करने के दौरान विश्व के सबसे ऊंचे पर्वत (एवरेस्ट) की खोज की गई थी।160 किलोमीटर से भी अधिक दूरी पर स्थित अलग-अलग छ: केंद्रों से इस पर्वत शिखर का नामकरण सर जॉर्ज एवरेस्ट के नाम पर किया गया जिसने सर्वप्रथम विशाल थियोडोलाइट को अधिकृत किया और उनका प्रयोग किया।अब ये थियोडोलाइट देहरादून में स्थित भारत सर्वेक्षण के संग्रहालय में प्रदर्शन के लिए रखे गए हैं।
- थियोडोलाइट (Theodolite):एक सर्वेक्षण यंत्र जो त्रिकोणमिति के नियमों पर आधारित है,का प्रयोग एक घूर्णी टेलिस्कोप से कोणों का मापन करने में किया जाता है।
(3.)उन्नयन कोण और अवनमन कोण (Angle of Elevation and Angle of Depression):
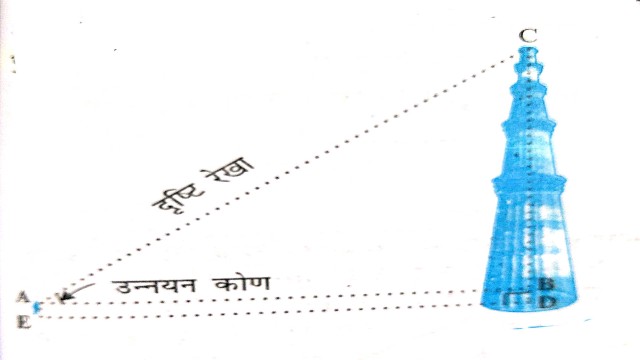
- इस आकृति में छात्र की आंख से मीनार के शिखर तक खींची गई रेखा AC को दृष्टि-रेखा (Line of Sight) कहा जाता है।छात्र मीनार के शिखर की ओर देख रहा है।दृष्टि-रेखा और क्षैतिज रेखा से बने कोण BAC को छात्र की आंख से मीनार के शिखर का उन्नयन कोण (Angle of Elevation) कहा जाता है।
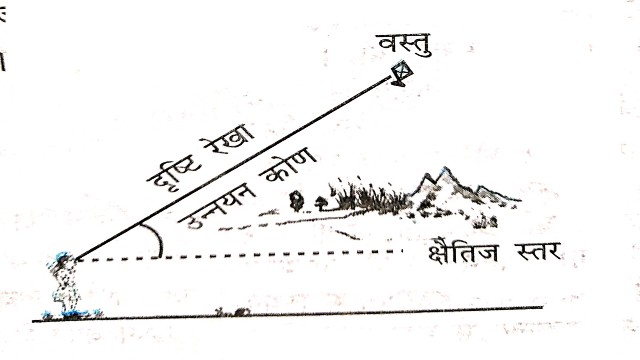
- इस प्रकार दृष्टि-रेखा प्रेक्षक की आँख के उस वस्तु के बिंदु को मिलाने वाली रेखा होती है जिसे प्रेक्षक देखता है।देखे गए बिंदु का उन्नयन कोण उस स्थिति में,दृष्टि रेखा क्षैतिज रेखा से बना कोण होता है जबकि देखा जा रहा बिंदु क्षैतिज स्तर से ऊपर होता है अर्थात् वह स्थिति जबकि वस्तु को देखने के लिए हमें अपना सिर उठाना होता है।
- बालकनी में बैठी लड़की मंदिर की सीढ़ी पर रखे गमले को नीचे की ओर देख रही है।इस स्थिति में दृष्टि-रेखा क्षैतिज स्तर से नीचे है।दृष्टि रेखा और क्षैतिज रेखा से इस प्रकार बने कोण को अवनमन कोण (Angle of Depression) कहा जाता है। अतः देखी जा रही वस्तु पर स्थित बिंदु का अवनमन कोण उस स्थिति में दृष्टि रेखा और क्षैतिज रेखा से बना कोण होता है जबकि क्षैतिज रेखा से नीचे होता है अर्थात् वह स्थिति जबकि देखे जाने वाले बिंदु को देखने के लिए हमें अपना सिर नीचे झुकाना होता है।
Also Read This Article:Complementary Angles in Trigonometry
(4.)त्रिकोणमितीय सारणियां (Trigonometric Tables):
- समकोण त्रिभुज में \sin\theta,\cos\theta,\tan\theta के अनुपात का मान भुजाओं की लंबाईयों पर निर्भर नहीं करता है बल्कि केवल कोणों पर निर्भर करता है।इन अनुपातों के मानों को 0° से 90° तक के सभी कोणों के लिए निकाल कर फिर सारणियाँ बनाई जाती है।ऐसी सारणियों को त्रिकोणमितीय सारणियाँ कहते हैं।इनकी मदद से किसी भी इच्छित अनुपात का मान ज्ञात कर सकते हैं।इन सारणियों से हम निम्न प्रकार मान प्राप्त करते हैं:
\sin60°=0.8660,\cos60°=0.5000,\tan60°=1.7321 - विशुद्ध मानों वाली त्रिकोणमितीय सारणियों का सृजन एक महत्त्वपूर्ण कार्य माना जाता था और इसने प्राचीनकाल के श्रेष्ठ गणितज्ञों को दिमागी तौर पर उलझाए रखा था।नाइकिया निवासी हिप्पार्कस (150 ईसा पूर्व);जो एक यूनानी गणितज्ञ था,संभवत पहला व्यक्ति था जिसने इन सारणियों की रचना की।उसने सूर्य और चांद के आकार तथा पृथ्वी से उनकी दूरियां मापने की कोशिश भी की थी।एक ऐसे गणित की आवश्यकता उसने महसूस की थी जिसके द्वारा पृथ्वी पर लिए गए मापों के आधार पर आकाशीय पिंडों का अनुमापन किया जा सके।त्रिकोणमिति की खोज का श्रेय उसे भी दिया जाता है।
- त्रिकोणमिति हमें समस्याओं के समाधान निकालने में कैसे मदद करती है?तो इसका उत्तर है उस विधि के द्वारा त्रिभुजन कहते हैं तथा जिसमें बहुत से त्रिभुजों के कोण मापकर फिर त्रिकोणमितीय सारणियों का इस्तेमाल किया जाता है।
- उपर्युक्त विवरण में त्रिकोणमिति (Trigonometry) के बारे में बताया गया है।
(5.)त्रिकोणमिति के सवाल (Trigonometry Questions):
- Example:1.कल्पना कीजिए कि दर्शक नदी के इस तरफ वाले किनारे के बिंदु ब पर खड़ा है।दूसरे किनारे पर वह बिंदु अ जैसे कि एक पेड़ को लेता है।अब \angle अ ब स को मापने पर उसका मान 72° आता है।दर्शक अब किनारे पर बढ़ते हुए बिन्दु स पर पहुंचता है जो नदी के किनारे पर स्थित बिंदु अ के ठीक आमने-सामने है।अतः
- \angleअ स ब=90°। अब ∆ अ ब स में \frac{\text{अ स}}{\text{ब स}}=\tan72°;\text{अ स}=30\tan72°
\Rightarrow30×3.077=92.310
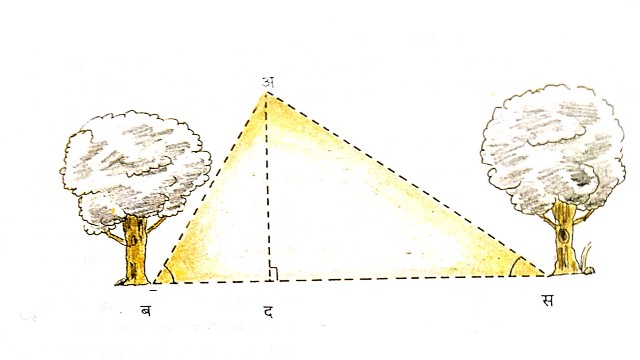
अतः नदी की चौड़ाई 92.310 मीटर है। - Example:2.मान लीजिए कि सर्वेक्षक ने दो बिंदुओं ब और स जो कि दो बड़े वृक्षों द्वारा दर्शाए गए हैं,के बीच की दूरी पहले ही ज्ञात कर ली है।वह अ ब,अ स तथा अ द की लंबाईयों को निकालना चाहता है।पर चूँकि बिंदु अ तक उसकी पहुंच नहीं है,वह इन दूरियों को सीधे-सीधे नहीं माप सकता। मगर कोणों \angleअ ब स और \angleअ स ब को तो वह माप ही सकता है।
- मान लीजिए कि ब स की लंबाई 100 मीटर है तथा \angleअ ब स=60°और \angleअ स ब=50° है।
त्रिकोणमितीय सारणियों की मदद से वह इन मानों को यूं निकाल लेता है:
\tan60°=1.732 और tan50°=1.1918 तब अ द की लंबाई को वह इस सह-संबंध द्वारा निकाल सकता है: - अ द=\frac{100(\tan60°×\tan50°)}{\tan60°+\tan50°}
अ द=\frac{100×1.7321×1.1918}{1.732+1.1918}=120.3 मीटर
अ ब=\frac{\text {अ द}}{\sin60°}
\Rightarrow\frac{120.372}{0.8690}=139 मीटर
अ ब=139 मीटर
अ स=\Rightarrow\frac{120.372}{0.7660}=157.14 मीटर
अ स=157.14 मीटर
2.त्रिकोणमिति (Trigonometry) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिकोणमिति क्या है? (What is Trigonometry?):
उत्तर:त्रिकोणमिति,गणित की शाखा कोणों के विशिष्ट फलनों और गणना के लिए उनके अनुप्रयोग से संबंधित है।सामान्यतः त्रिकोणमिति में उपयोग किए जाने वाले कोण के छह फलन होते हैं।उनके नाम और संक्षिप्त नाम sine (sin),cosine (cos),tangent (tan),cotangent (cot), secant (sec), and cosecant (csc) हैं।
प्रश्न:2.त्रिकोणमिति का उद्देश्य क्या है? (What is the Purpose?):
उत्तर:उद्देश्य (Purpose)
त्रिकोणमितीय फलनों का उपयोग ज्यामितीय आकृतियों में ज्ञात या मापे गए कोणों से अज्ञात कोणों और दूरी प्राप्त करने में किया जाता है। त्रिकोणमिति खगोल विज्ञान (astronomy),मानचित्रण,सर्वेक्षण (surveying) और तोपखाने रेंज (artillery range) खोज के रूप में ऐसे क्षेत्रों में कोणों और दूरी की गणना करने की जरूरत से विकसित की है।
प्रश्न:3.त्रिकोणमिति का आविष्कार किसने किया? (Who invented Trigonometry?):
उत्तर:त्रिकोणमिति का उद्देश्य
रचयिता
हिप्पार्कस (Hipparchus)
“यहां तक कि अगर वह यह आविष्कार नहीं किया था, Hipparchus त्रिकोणमिति के जिसका व्यवस्थित उपयोग के पहले व्यक्ति थे जिसका दस्तावेजी सबूत है.”(हीथ 257 (Heath 257)) कुछ इतिहासकार जहां तक कहते हैं कि उन्होंने त्रिकोणमिति का आविष्कार किया है। हिपआर्कस के जीवन के बारे में ज्यादा जानकारी नहीं है।ऐसा माना जाता है कि उनका जन्म बिठिया के निकेया (Nicaea in Bithynia) में हुआ था।
प्रश्न:4.त्रिकोणमिति का सूत्र क्या है? (What is the Formula of Trigonometry?):
उत्तर:त्रिकोणमिति के निर्माता
नियम
त्रिकोणमिति अनुपात के लिए त्रिकोणमिति सूत्र जब कोण इसके अलावा दिए हुए होते हैं,के रूप में दिए जाते हैं,\sin(x+ y) = \sin(x) \cos(y)+\cos(x) \sin(y)
\cos(x+ y)=\cos (x) \cos (y)-\sin(x)\sin(y) ,\tan(x + y) =\frac {\tan x+\tan y}{1-\tan x \tan y}
प्रश्न:5.तीन बुनियादी त्रिकोणमिति फार्मूला क्या है? (What is three basic Trigonometry formula?):
उत्तर:त्रिकोणमिति का सूत्र
तीन फलन
तीन बुनियादी त्रिकोणमितीय फलन साइन (sine), कोसाइन (cosine) और टेन्जेन्ट (tangent) फलन हैं।ज्या फलन (sine function) को देखकर शुरू करते हैं।
प्रश्न:6.त्रिकोणमिति की मूल बातें क्या है? (What is the basics of trigonometry?):
उत्तर:त्रिकोणमिति मूल बातें
त्रिकोणमिति में तीन बुनियादी फलन साइन (sine),कोसाइन (cosine) और टेन्जेन्ट (tangent) हैं।इन तीन फलनों के आधार पर अन्य तीन फलन जो कोटैंजेंट (cotangent),सेकेंट (secant) और कॉसेकेंट (cosecant) हैं,प्राप्त किए जाते हैं।सभी त्रिकोणमितीय अवधारणाएं इन फलनों पर आधारित हैं।
प्रश्न:7.त्रिकोणमिति सूत्र क्या है? (What is trigonometry formula?):
उत्तर:त्रिकोणमिति सूत्र त्रिकोणमिति सर्वसमिका से जुड़े विभिन्न सूत्रों के सेट हैं,जिनका उपयोग समकोण त्रिभुज की भुजाओं और कोणों के आधार पर समस्याओं को हल करने के लिए किया जाता है।इन त्रिकोणमिति सूत्रों में दिए गए कोणों के लिए साइन (sine),कॉसाइन (cosine), टेन्जेन्ट (tangent), कॉसेकेंट (cosecant), सेकेंट (secant), कोटैंजेंट (cotangent) जैसे त्रिकोणमितीय फलन शामिल हैं।
प्रश्न:8.क्या त्रिकोणमिति SOH CAH TOA है? (Is trigonometry SOH CAH TOA?):
उत्तर:Sohcahtoa:SOHCAHTOA एक स्नेमोनिक डिवाइस (mnemonic device) है जिसका उपयोग गणित में तीन सबसे आम त्रिकोणमितीय फलनों की परिभाषाओं को याद रखने के लिए किया जाता है।
Soh…Sine = \frac{Opposite}{Hypotenuse}…cah…Cosine = \frac{Adjacent}{Hypotenuse}…toa\quad Tangent=\frac{Opposite}{Adjacent}
प्रश्न:9.त्रिकोणमिति को हल करने का सबसे आसान तरीका क्या है? (What is the easiest way to solve trigonometry?):
उत्तर:त्रिकोणमिति को जीतने के 11 टिप्स
Tip 1) हमेशा अधिक जटिल पक्ष से शुरू करें।
Tip 2) साइन और कोसाइन में सबको व्यक्त करें।
Tip 3) पदों को एक ही भिन्न में मिलाएं।
Tip 4) sin²x और cos²x के बीच बदलने के लिए पाइथागोरस आइडेंटिटिज (Pythagorean Identities) का इस्तेमाल करें।
Tip 5) यह जानों कि कब डबल कोण फार्मूला लागू करना है (DAF (Double Angel Formula))
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिकोणमिति (Trigonometry) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Trigonometry
त्रिकोणमिति (Trigonometry)
Trigonometry
त्रिकोणमिति (Trigonometry) या त्रिभुज मापन ज्यामिति की एक महत्त्वपूर्ण शाखा है।त्रिभुजों के कुछ कोण या भुजाएं ज्ञात होने पर शेष कोणों और भुजाओं का मान हम त्रिकोणमिति की सर्वसमिकाओं तथा न्यून कोणों के त्रिकोणमितीय अनुपातों द्वारा निकाल सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
