Function in Maths Class 11
1.गणित में फलन कक्षा (Function in Maths Class 11),गणित में फलन (Function in Mathematics):
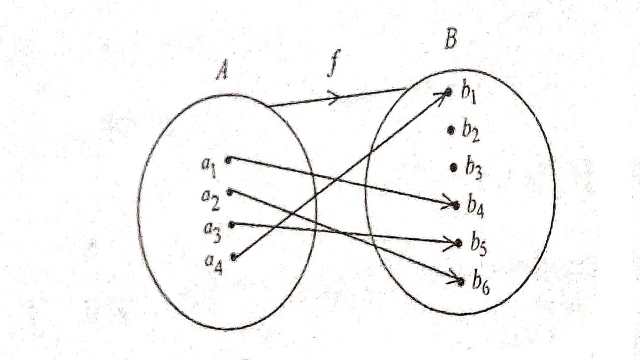
गणित में फलन कक्षा (Function in Maths Class 11) की परिभाषा इस प्रकार है।एक समुच्चय A से समुच्चय B का सम्बन्ध f एक फलन कहलाता है यदि समुच्चय A के प्रत्येक अवयव का समुच्चय B में एक और केवल एक प्रतिबिम्ब होता है।
दूसरों शब्दों में फलन f किसी अरिक्त समुच्चय A से एक अरिक्त समुच्चय B का है, इस प्रकार का सम्बन्ध कि f का प्रान्त A है तथा f के किसी भी दो भिन्न क्रमित युग्मों के प्रथम घटक समान नहीं है।
यदि f, A से B का एक फलन है तथा (a, b) \in f तो f(a)=b, जहाँ b को f के अन्तर्गत a प्रतिबिम्ब तथा a को b का पूर्व प्रतिबिम्ब कहते हैं।
A से B के फलन को प्रतीकात्मक रूप में f: A \rightarrow B निरूपित करते हैं।
वास्तविक मान फलन:
एक ऐसे फलन को जिसका परिसर वास्तविक संख्याओं का समुच्चय या उसका कोई उपसमुच्चय हो,वास्तविक मान फलन कहते हैं। यदि वास्तविक चर वाले किसी वास्तविक मान फलन का प्रान्त भी वास्तविक संख्याओं का समुच्चय अथवा उसका कोई उपसमुच्चय हो तो इसे वास्तविक फलन कहते हैं।
कुछ फलन और उनके आलेख (Some Functions and their Graphs):
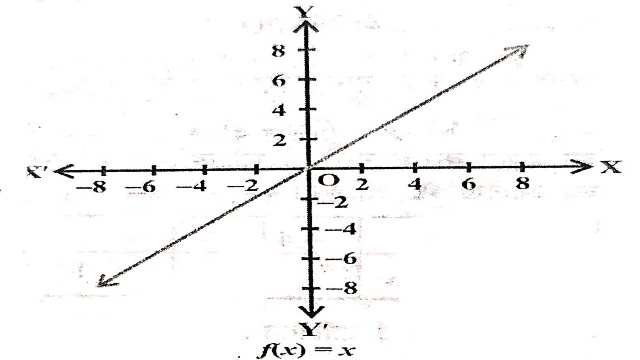
(1.)तत्समक फलन (Identity Function):
मान लीजिए R वास्तविक फलन है। y=f(x) प्रत्येक x \in R द्वारा परिभाषित एक वास्तविक मान फलन f: R \rightarrow R है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर f प्रान्त तथा परिसर R है। इसका आलेख एक सरल रेखा होता है। यह रेखा मूलबिन्दु से होकर जाती है।
(2.)अचर फलन (Constant Function):
y=f(x)=c जहाँ c एक अचर है और प्रत्येक x \in R द्वारा परिभाषित एक वास्तविक मान फलन f: R \rightarrow R है। यहाँ पर f का प्रान्त R है और उसका परिसर {c} है। f का आलेख x-अक्ष के समान्तर एक रेखा है। उदाहरण के लिए f(x)=3 प्रत्येक x \in R है तो इसका आलेख आकृति में दर्शायी रेखा है।
(3.)बहुपद फलन या बहुपदीय फलन (Polynomial Function):
फलन f: R \rightarrow R एक बहुपदीय फलन कहलाता है यदि R के प्रत्येक x के लिए y=f(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} जहाँ n एक ऋणेतर पूर्णांक है तथा a_{0}, a_{1}, a_{2}, a_{3},\cdots, a_{n} \in R
(4.)परिमेय फलन (Rational Functions):
\frac{f(x)}{g(x)} के प्रकार के फलन जहाँ f(x) तथा g(x) एक प्रान्त में x के परिभाषित बहुपदीय फलन है जिसमें g(x) \neq 0 परिमेय फलन कहलाते हैं।
(5.)मापांक फलन (Modulus Functions):
f(x)=|x| प्रत्येक x \in R द्वारा परिभाषित फलन f: R \rightarrow R मापांक फलन कहलाता है। x के प्रत्येक ऋणेतर मान के लिए f(x), x के बराबर होता है। परन्तु x के ऋण मानों के लिए, f(x) का मान x के मान के ऋण के बराबर होता है अर्थात्
f(x)=\left\{\begin{array}{l} x, x \geq 0 \\ -x, x<0 \end{array}\right.
मापांक फलन का आलेख आकृति में दिया गया है। मापांक फलन को निरपेक्ष मान फलन भी कहते हैं।
(6.)चिन्ह फलन (signum Functions):
प्रत्येक x \in R के लिए
f(x)=\left\{\begin{array}{l} 1, \text { यदि } x>0 \\ 0, \text { यदि } x=0 \\ -1, \text { यदि } x<0 \end{array}\right.
द्वारा परिभाषित फलन f: R \rightarrow R चिन्ह फलन कहलाता है। चिन्ह फलन का प्रान्त R है। परिसर समुच्चय {-1,0,1} है। आकृति में चिन्ह फलन का आलेख दर्शाया गया है।
(7.)महत्तम पूर्णांक फलन (Greatest Integer Functions):
f(x)=[x], x \in R द्वारा परिभाषित फलन f: R \rightarrow R, x से कम या x के बराबर महत्तम पूर्णांक का मान ग्रहण (धारण) करता है ऐसा फलन महत्तम पूर्णांक फलन कहलाता है। [x] की परिभाषा से हम देख सकते हैं कि
\left.\begin{array}{l} {[x]=-1 \text { यदि }-1 \leq x<0} \\ {[x]=0 \text { यदि } 0 \leq x<1} \\ {[x]=1 \text { यदि } 1 \leq x<2} \\ {[x]=2 \text { यदि } 2 \leq x<3 \text { इत्यादि }} \end{array}\right.
इस फलन का आलेख आकृति में दर्शाया गया है।
वास्तविक फलनों का बीजगणित (Algebra Between Functions):
इस अनुच्छेद में हम सीखेंगे कि किस प्रकार दो वास्तविक फलनों को जोड़ा जाता है, एक वास्तविक फलन को दूसरे से घटाया जाता है,एक वास्तविक फलन को किसी अदिश (यहाँ अदिश का अभिप्राय वास्तविक संख्या से है) से गुणा किया जाता है ;दो वास्तविक फलनों का गुणा किया जाता है तथा एक वास्तविक फलन को दूसरे से भाग दिया जाता है।
(1.)दो वास्तविक फलनों का योग
मान लीजिए कि f: X \rightarrow R तथा g : X \rightarrow R कोई दो वास्तविक फलन हैं जहाँ X \subset R तब हम (f+g): X \rightarrow R को सभी x \in X के लिए (f+g) (x)=f(x) +g(x) द्वारा परिभाषित करते हैं।
(2.)एक वास्तविक फलन में से दूसरे को घटाना
मान लीजिए कि f: X \rightarrow R तथा g: X \rightarrow R कोई दो वास्तविक फलन हैं जहाँ X \subset R तब हम (f-g) : X \rightarrow R को सभी x \in X के लिए (f-g)(x)=f(x)-g(x) द्वारा परिभाषित करते हैं।
(3.)एक अदिश से गुणा
मान लीजिए कि f : X \rightarrow R एक वास्तविक मान फलन है तथा \alpha एक अदिश राशि है। यहाँ अदिश से हमारा अभिप्राय किसी वास्तविक संख्या से है। तब गुणनफल \alpha ,X से R में एक फलन है जो (\alpha f)(x)=\alpha f(x), x \in R से परिभाषित होता है।
(4.)दो वास्तविक फलनों का गुणन दो वास्तविक फलनों f : X \rightarrow R तथा g : X \rightarrow R का गुणनफल (या गुणा) एक फलन fg : X \rightarrow R है जो सभी (fg)(x)=f(x)g(x) ;x \subset R द्वारा परिभाषित है। इसे बिन्दुशः गुणन भी कहते हैं।
(5.)दो वास्तविक फलनों का भागफल मान लीजिए कि f तथा g, X \rightarrow R द्वारा परिभाषित, दो वास्तविक फलन हैं जहाँ X \subset R. f का g से भागफल है जिसे \frac{f}{g} से निरूपित करते हैं, एक फलन है जो सभी x \in X जहाँ g(x) \neq 0 के लिए \left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}, द्वारा परिभाषित है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Relation in Maths Class 11
2.गणित में फलन कक्षा पर आधारित उदाहरण (Examples Based on Function in Maths Class 11):
Example:1.निम्नलिखित सम्बन्धों में कौनसे फलन हैं? कारण का उल्लेख कीजिए। यदि सम्बन्ध एक फलन है तो उसका परिसर निर्धारित कीजिए।
(i) {(2,1),(5,1),(8,1),(11,1),(14,1),(17,1)}
Solution:{(2,1),(5,1),(8,1),(11,1),(14,1),(17,1)}
इसके प्रान्त के प्रत्येक अवयव का अद्वितीय प्रतिबिम्ब है,अतः यह फलन है।
प्रान्त={2,5,8,11}
परिसर={1}
(ii) {(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}
Solution:{(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}
इसके प्रान्त के प्रत्येक अवयव का अद्वितीय प्रतिबिम्ब है,अतः यह फलन है।
प्रान्त ={4,6,8,10,12,14}
परिसर={1,2,3,4,5,6,7}
(iii){(1,3),(1,5),(2,5)}
Solution:{(1,3),(1,5),(2,5)}फलन नहीं है। क्योंकि इसके प्रान्त का अवयव 1 के दो प्रतिबिम्ब है अर्थात् अद्वितीय प्रतिबिम्ब नहीं है।
Example:2.निम्नलिखित वास्तविक फलनों के प्रान्त तथा परिसर ज्ञात कीजिए:
(i)f(x)=-|x|
Solution: f(x)=-|x|
स्पष्ट है कि f(x)=-|x| \leq 0: \forall x \in R
f का प्रान्त=R, तथा f का परिसर=\{x \in R: x \leq 0\}=R^{-}=(-\infty, 0)
(ii) f(x)=\sqrt{9-x^{2}}
Solution: f(x)=\sqrt{9-x^{2}}
f(x) परिभाषित नहीं है जब 9-x^{2}<0\\ \Rightarrow x^{2} > 9\\ \Rightarrow x>3 और x<-3
f(x) परिभाषित है जब -3 \leq x \leq 3
\therefore f का प्रान्त -3 \leq x \leq 3 , x \in R
अब माना कि y=\sqrt{9-x^{2}}\\ \Rightarrow y^{2}=9-x^{2}\\ \Rightarrow x^{2}=9-y^{2} \\ \therefore x=\sqrt{9-y^{2}}
f(x) परिभाषित है यदि 9-y^{2} \geq 0 \\ \Rightarrow y^{2} \leq 9\\ \Rightarrow y \leq 3, y \neq \text { Negative }
f का परिसर =y \leq 3 और y \geq 0 \\ =\{y: y \in R \text {और } 0 \leq y \leq 3\}
Example:3.एक फलन f(x) =2x-5 द्वारा परिभाषित है।निम्नलिखित के मान ज्ञात कीजिए:
(i) f(0)
Solution:f(x) =2x-5
f(0)=2×0-5
=-5
(ii) f(7)
Solution:f(x) =2x-5
f(7)=2×7-5=9
(iii) f(-3)
Solution:f(x) =2x-5
f(-3)=2×-3-5
=-6-5
=-11
Example:4.फलन ‘t’ सेल्शियस तापमान का फारेनहाइट तापमान में प्रतिचित्रण करता है जो t(c)=\frac{9 C}{5}+32 द्वारा परिभाषित है निम्नलिखित को ज्ञात कीजिए:
(i) t(0)
Solution: t(C)=\frac{9 C}{5}+32 \\ \Rightarrow t(0)=\frac{9(0)}{5}+32=32
(ii) t(28)
Solution: t(C)=\frac{9C}{5}+32 \\ \Rightarrow t(28)=\frac{9 \times 28}{5}+32 \\ =\frac{252}{5}+32 \\ =50.4+32 \\ \Rightarrow t(28)=82.4
(iii) t(-10)
Solution: t(C)=\frac{9 C}{5}+32 \\ \Rightarrow t(-10)=\frac{9 \times-10}{5}=32 \\ =-18+32 \\ \Rightarrow t(-10)=14
(iv) c का मान जब t(C)=212 \\ t(C)=\frac{9 C}{5}+32 \\ \Rightarrow 212=\frac{9 C}{5}+32 \\ \Rightarrow \frac{9 C}{5}=212-32 \\ \Rightarrow \frac{9 C}{5}=180 \\ \Rightarrow C=\frac{180 \times 5}{9} \\ \Rightarrow C=100
Example:5.निम्नलिखित में से प्रत्येक का परिसर ज्ञात कीजिए:
(i)f(x)=2-3 x, x \in R, x>0
Solution: जब x>0
तो f(x) =2-3x<0
अतः परिसर=(-\infty, 2)
(ii)f(x)=x^{2}+2,x एक वास्तविक संख्या है।
Solution: f(x)=x^{2}+2, x \in R
अतः परिसर=[2, \infty)
(iii) f(x)=x, x एक वास्तविक संख्या है।
Solution:f(x)=x, x \in R
अतः परिसर=R
उपर्युक्त उदाहरणों के द्वारा गणित में फलन कक्षा (Function in Maths Class 11),गणित में फलन (Function in Mathematics) को समझ सकते हैं।
3.गणित में फलन कक्षा के सवाल (Function in Maths Class 11 Questions):
(1.)यदि f: R \rightarrow R, f(x)=x^{2} हो तो परिसर ज्ञात कीजिए।
(2.)यदि f: R^{+} \rightarrow R जहाँ f(x)=\log x जहाँ R^{+} धनात्मक वास्तविक संख्याओं का समुच्चय है, f(R^{+}) ज्ञात कीजिए।
(1)परिसर=\{x \in R \mid 0 \leq x < \infty\}
(2) f का परिसर=f(x)=R
उपर्युक्त सवालों को हल करने पर गणित में फलन कक्षा (Function in Maths Class 11),गणित में फलन (Function in Mathematics) को ठीक से समझ सकते हैं।
Also Read This Article:-Relation Class 11
4.गणित में फलन कक्षा (Function in Maths Class 11),गणित में फलन (Function in Mathematics) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.फलन कितने प्रकार के होते हैं उनकी परिभाषा लिखिए (Write down definition of how many types of functions are there):
उत्तर:(1.)एकैकी फलन (one-one Function or Injective Function):
यदि f : A \rightarrow B एक फलन हो तो f एकैकी फलन कहलाता है यदि f के अन्तर्गत A के भिन्न-भिन्न अवयवों के B में भिन्न-भिन्न प्रतिबिम्ब हों। अर्थात् f : A \rightarrow B एकैकी है यदि a \neq b \Rightarrow f(a) \neq f (b) \forall a, b \in A
दूसरे शब्दों में
f : A \rightarrow B एकैकी है यदि f(a)=f (b) \Rightarrow a=b \forall a,b \in A
(2.)बहु-एकी फलन (Many-one Function)
समुच्चय A से समुच्चय B में परिभाषित कोई फलन f बहु-एकी फलन कहलाता है यदि f के अन्तर्गत A के दो या अधिक अवयवों का B में एक प्रतिबिम्ब है। अतः f : A \rightarrow B बहु-एकी फलन है यदि A में कम से कम दो a और b ऐसे अवयव विद्यमान है a \neq b कि परन्तु f(a)=f(b)
इस प्रकार यदि f : A \rightarrow B एक एकैकी फलन नहीं है तो वह अवश्य ही बहु-एकी फलन होगा।
(3.)आच्छादक फलन (Onto Function or Surjection):
समुच्चय A से समुच्चय B में परिभाषित कोई फलन f आच्छादक कहलाता है यदि B का प्रत्येक अवयव A के किसी न किसी अवयव का प्रतिबिम्ब हो अर्थात् B के प्रत्येक अवयव का A में कम से कम एक पूर्व-प्रतिबिम्ब वर्तमान हो।
अतः f : A \rightarrow B एक आच्छादक फलन होगा यदि b \in B \Rightarrow \exists a \in A ताकि f(a)=b
स्पष्टतः यदि f आच्छादक है तब f(A)=B अर्थात् f का सहप्रान्त=f का परिसर
टिप्पणी:यदि किसी फलन f : A \rightarrow B के लिए f के सहप्रान्त तथा परिसर बराबर नहीं है तो f आच्छादक नहीं होगा।
(4.)अर्न्तक्षेपी फलन (Into Function):
समुच्चय A से समुच्चय B में परिभाषित कोई फलन f एक अर्न्तक्षेपी फलन कहलाता है यदि कम से कम एक ऐसा अवयव विद्यमान हो जो A के किसी अवयव का प्रतिबिम्ब नहीं हो अर्थात् जिसका पूर्व प्रतिबिम्ब विद्यमान नहीं हो।
अतः f अर्न्तक्षेपी है यदि f(A) \neq B
(5.)एकैकी आच्छादक फलन (one-one onto function or Bijection):
समुच्चय A से समुच्चय B में परिभाषित कोई फलन f एकैकी आच्छादक कहलाता है यदि f एकैकी के साथ-साथ आच्छादक भी हो। अर्थात् f : A \rightarrow B एक एकैकी आच्छादक फलन होगा यदि
(a) f एकैकी है अर्थात् f(a)=f(b) \Rightarrow a=b \forall a, b \in A
(b) f आच्छादक है अर्थात् \forall b \in B \Rightarrow \exists a \in A ताकि f(a)=b
प्रश्न:2.फलन के प्रतिलोम प्रतिबिम्ब से क्या तात्पर्य है? (What is meant by Inverse image?):
उत्तर:माना f : X \rightarrow Y समुच्चय X से समुच्चय Y में एक फलन है तथा y \in Y । तब समुच्चय X के सभी अवयवों का समुच्चय जिनका f-प्रतिबिम्ब यह अवयव y है, y का प्रतिलोम प्रतिबिम्ब (Inverse image) कहलाता है तथा इसे f^{-1}(y) द्वारा निरूपित किया जाता है। अतः f^{-1}(y)={x \in X: f(x)=y} \Rightarrow f^{-1}(y) \subseteq X
प्रश्न:3.फलन का प्रान्त,सहप्रान्त और परिसर किसे कहते हैं? (What is domain Co-domain and range of function called?):
उत्तर:यदि f समुच्चय A से समुच्चय B में परिभाषित कोई फलन है तो समुच्चय A को फलन f का प्रान्त तथा समुच्चय B को फलन f का सहप्रान्त कहते हैं। समुच्चय B के उन सभी अवयवों का समुच्चय जो A के अवयवों के प्रतिबिम्ब है, f का परिसर कहलाता है। इसे f(A) द्वारा प्रदर्शित किया जाता है। अर्थात् फलन f का परिसर B के उन अवयवों का समुच्चय है जिनके पूर्व-प्रतिबिम्ब A में विद्यमान हैं।
अतः f(A)=\{f(a), a \in A\} स्पष्टतः f(A) \subseteq B
यदि फलन को क्रमित युग्मों के समुच्चय के रूप में व्यक्त किया गया हो तो f के क्रमित युग्मों के प्रथम अवयवों का समुच्चय f का प्रान्त तथा इन युग्मों के द्वितीय अवयवों का समुच्चय f का परिसर कहलाता है। अर्थात्
f का प्रान्त=\{a \mid(a, b) \in A\}, f का परिसर=\{b \mid(a, b) \in f\}
उपर्युक्त प्रश्नों के उत्तर द्वारा गणित में फलन कक्षा (Function in Maths Class 11),गणित में फलन (Function in Mathematics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Function in Maths Class 11
गणित में फलन कक्षा
(Function in Maths Class 11)
Function in Maths Class 11
गणित में फलन कक्षा (Function in Maths Class 11) की परिभाषा इस प्रकार है।एक समुच्चय A
से समुच्चय B का सम्बन्ध f एक फलन कहलाता है यदि समुच्चय A के प्रत्येक अवयव का समुच्चय B
में एक और केवल एक प्रतिबिम्ब होता है।
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
