Parallelogram in Class 9th
1.कक्षा 9वीं में समान्तर चतुर्भुज (Parallelogram in Class 9th),समान्तर चतुर्भुज कक्षा 9 (Parallelogram Class 9):
कक्षा 9वीं में समान्तर चतुर्भुज (Parallelogram in Class 9th) के इस आर्टिकल में समान्तर चतुर्भुज व उसके गुणधर्मों पर आधारित कुछ महत्त्वपूर्ण सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Inequalities in Triangles in Class 9th
2.कक्षा 9वीं में समान्तर चतुर्भुज के साधित उदाहरण (Parallelogram in Class 9th Solved Illustrations):
Illustration:1.एक समान्तर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं जो OA=3 cm और OD=2 cm है,तो AC और BD की लम्बाई ज्ञात कीजिए।
Solution:AC=2 OA=2×3=6 cm
BD=2 OD=2×2=4 cm (समान्तर चतुर्भुज के विकर्ण आपस में समद्विभाजित करते हैं)
Illustration:2.एक समान्तर चतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
Solution:कथन असत्य है।समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
Illustration:3.क्या कोण 110°,80°,70° और 95° किसी चतुर्भुज के कोण हो सकते हैं? क्यों और क्यों नहीं?
उत्तर:110°+80°+70°+95°=355°
नहीं हो सकते हैं,क्योंकि किसी भी चतुर्भुज के चारों कोणों का योग 360° होता है।
Illustration:4.क्या किसी चतुर्भुज के सभी कोण अधिक कोण हो सकते हैं? अपने उत्तर के लिए कारण दीजिए।
Solution:सभी कोण अधिक कोण नहीं हो सकते हैं क्योंकि सभी कोणों का योग 360° से अधिक हो जाएगा जो चतुर्भुज के लिए सम्भव नहीं है।
Illustration:5.एक चतुर्भुज का एक कोण 108° है तथा अन्य तीनों कोण बराबर हैं।तीनों बराबर कोणों में से प्रत्येक को ज्ञात कीजिए।
Solution:चतुर्भुज के शेष तीनों कोणों का योग=360°-108°=252°
प्रत्येक कोण=\frac{252^{\circ}}{3}=84^{\circ}
Illustration:6.ABCD एक समलम्ब है जिसमें AB \| DC और \angle A=\angle B=45^{\circ} है।इस समलम्ब के कोण C और D ज्ञात कीजिए।
Solution: \angle A+\angle B=45^{\circ}+45^{\circ}=90^{\circ} \\ \angle C+\angle D= 360^{\circ}-90^{\circ}=270^{\circ} \\ \Rightarrow \angle C=\angle D=\frac{270^{\circ}}{2}=135^{\circ}
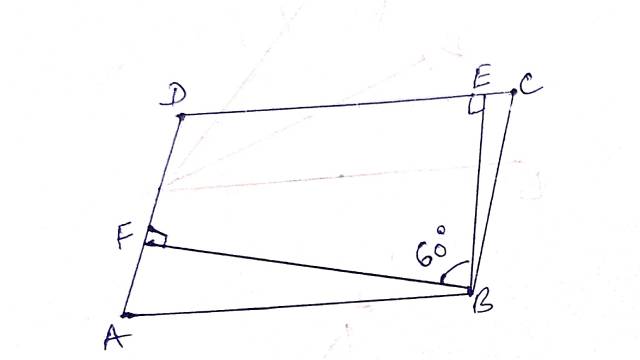
Illustration:7.एक समान्तर चतुर्भुज के एक अधिक कोण के शीर्ष से खींचे गए उस समान्तर चतुर्भुज के दो शीर्षलम्बों के बीच का कोण 60° है।इस समान्तर चतुर्भुज के सभी कोण ज्ञात कीजिए।
Solution: AF \| BC तथा BF इनको काटती है।
\angle BFA=\angle FBC (एकान्तर कोण)
\angle FBC=90^{\circ}\left(\because \angle BFA=90^{\circ}\right) \\ \Rightarrow \angle FBE+\angle EBC=90^{\circ} \\ \Rightarrow 60^{\circ}+\angle EBC=90^{\circ} \\ \Rightarrow \angle EBC=90^{\circ} -60^{\circ}=30^{\circ} \\ \triangle BCE में
\angle EBC+\angle BEC+\angle C=180^{\circ} \\ 30^{\circ}+90^{\circ}+\angle C=180^{\circ} \\ \Rightarrow \angle C=180^{\circ}-120^{\circ}=60^{\circ} \\ \angle A=\angle B (स.च. के सम्मुख कोण)
अतः \angle A=\angle B=60^{\circ} \\ \angle A +\angle B=180^{\circ} (स.च. के आसन्न कोण)
60^{\circ}+\angle B=180^{\circ} \\ \Rightarrow \angle B=180^{\circ}-60^{\circ}=120^{\circ} \\ \angle B=\angle D=120^{\circ} (स.च. के सम्मुख कोण)
अतः समान्तर चतुर्भुज के चारों कोण 60°,120°,60°,120° होंगे।
Illustration:8.एक चतुर्भुज ABCD के तीन कोण बराबर हैं।क्या यह एक समान्तर चतुर्भुज है?
Solution:नहीं,इसका समान्तर चतुर्भुज होना आवश्यक नहीं है।
Illustration:9.चतुर्भुज ABCD में, \angle A+\angle D=180^{\circ} है।इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
Solution:समान्तर चतुर्भुज के आसन्न कोणों का योग 180° होता है।अतः यह समान्तर चतुर्भुज है।
Illustration:10.ABCD एक समान्तर चतुर्भुज है।यदि इसके विकर्ण बराबर हैं,तो का मान ज्ञात कीजिए।
Solution:समान्तर चतुर्भुज के विकर्ण बराबर हों,तो वह आयत होता है अतः \angle ABC=90^{\circ}
Illustration:11.एक समचतुर्भुज के विकर्ण परस्पर बराबर और लम्ब होते हैं।क्या यह कथन सत्य है।अपने उत्तर के लिए कारण दीजिए।
Solution:यह कथन असत्य है,क्योंकि समचतुर्भुज के विकर्ण परस्पर लम्ब होते हैं,परन्तु बराबर नहीं होते हैं।
Illustration:12.एक चतुर्भुज के सभी कोण बराबर हैं।इस चतुर्भुज को कौन-सा विशेष नाम दिया गया है?
Solution:यह आयत या वर्ग हो सकता है।
Illustration:13.एक आयत के विकर्ण परस्पर बराबर और लम्ब हैं।क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
Solution:यह कथन असत्य है क्योंकि आयत के विकर्ण बराबर तो होते हैं परन्तु लम्ब नहीं होते हैं।
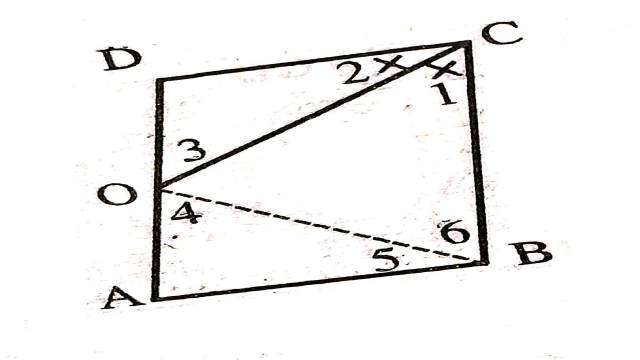
Illustration:14.आकृति में समान्तर चतुर्भुज ABCD के \angle BCD का अर्द्धक AD के मध्य बिन्दु O से गुजरता है।सिद्ध कीजिए कि OB, \angle ABC का अर्द्धक है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD में \angle 1=\angle 2 तथा AO=OD
सिद्ध करना है (To Prove): \angle 5=\angle 6
उपपत्ति (Proof): BC \| AD तथा CO इन्हें काटती है।
\therefore \angle 1=\angle 3 (एकान्तर कोण)
लेकिन \angle 1=\angle 2 (दिया है)
\because CO, \angle C का अर्द्धक है।
\therefore \angle 2=\angle 3 \Rightarrow DC=OD \cdots(1) \\ \because DC=A B (स. च. की सम्मुख भुजाएँ)… (2)
तथा OD=OA (दिया है) ….. (3)
\therefore (1),(2),(3) से OA=OB \\ \Rightarrow \angle 4=\angle 5 \cdots(4)
लेकिन \angle 4=\angle 6 (एकान्तर कोण) …..(5)
(4) तथा (5) से:
\angle 5=\angle 6 \\ \Rightarrow OB, \angle ABC का अर्द्धक है।
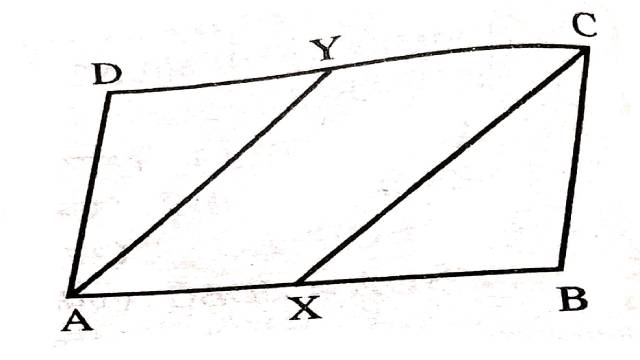
Illustration:15.आकृति में,ABCD एक समान्तर चतुर्भुज है।X और Y क्रमशः भुजाओं AB और CD के मध्य बिन्दु हैं तो सिद्ध कीजिए कि AXCY एक समान्तर चतुर्भुज है।
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है।X और Y क्रमशः भुजाओं AB और CD के मध्य बिन्दु हैं।XC और AY को मिलाया गया है।
सिद्ध करना है (To Prove):AXCY एक समान्तर चतुर्भुज है।
उपपत्ति (Proof):AB=CD (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
तथा AB \| CD (दिया हुआ है)
\therefore AX=CY
और AX \| CY
अतः AXCY एक समान्तर चतुर्भुज होगा।
Illustration:16.आकृति में,ABCD एक समान्तर चतुर्भुज है।B से CD पर लम्ब BE खींचा गया है जो CD को E पर मिलता है। सिद्ध कीजिए ABED एक समलम्ब चतुर्भुज होगा।
Solution:दिया है (Given):आकृति में ABCD एक समान्तर चतुर्भुज है।B से लम्ब BE भुजा CD को E पर मिलता है।
सिद्ध करना है (To Prove):ABED एक समान्तर चतुर्भुज है।
उपपत्ति (Proof): AB \| CD (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
\therefore AB \| ED \\ \because DA \| BC अतः AD,BE के समान्तर नहीं है।
\therefore भुजाओं का युग्म समान्तर है।
अतः ABED एक समलम्ब चतुर्भुज है।
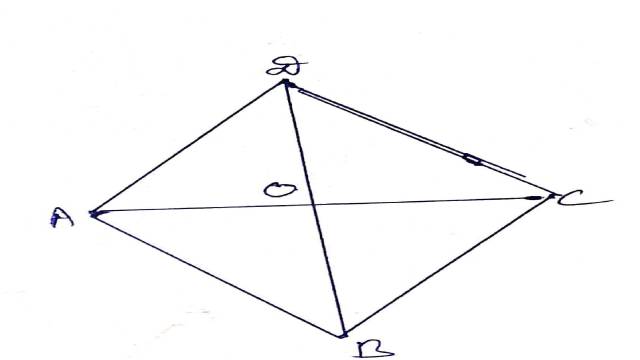
Illustration:17.यदि समान्तर चतुर्भुज का एक विकर्ण,उसके एक कोण को समद्विभाजित करता है तो वह दूसरे कोण को भी समद्विभाजित करेगा।और तब दोनों विकर्ण एक-दूसरे पर लम्ब होंगे,सिद्ध कीजिए।
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है तथा \angle ABO=\angle CBO, \angle ADO=\angle CDO
सिद्ध करना है (To Prove): AC \perp BD
उपपत्ति (Proof): \angle B=\angle D (समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं)……..(1)
\angle ABO=\angle CBO तथा \angle ADO=\angle CDO (दिया है)………..(2)
(1) व (2) से:
\angle ABO=\angle CBO=\angle ADO=\angle CDO \cdots(3)
अतः AB=AD (बराबर कोण की अभिमुख भुजाएँ) ……..(4)
\triangle ABO तथा \triangle ADO में
AB=AD (सिद्ध किया है)
OA=OA (उभनिष्ठ भुजा है)
BO=DO (स.च. के विकर्ण आपस में समद्विभाजित करते हैं)
SSS सर्वांगसमता नियम से
\triangle ABO \cong \triangle ADO
\angle AOB=\angle AOD (CPCT से)
परन्तु \angle AOB+\angle AOD=180^{\circ} (रैखिक कोण युग्म)……..(6)
(5) व (6) से:
\angle AOB=\angle AOD=90^{\circ}
अतः AO \perp BD
फलतः AC \perp BD
उपर्युक्त उदाहरणों के द्वारा कक्षा 9वीं में समान्तर चतुर्भुज (Parallelogram in Class 9th),समान्तर चतुर्भुज कक्षा 9 (Parallelogram Class 9) को समझ सकते हैं।
Also Read This Article:- Examples of Inequalities in Triangles
3.कक्षा 9वीं में समान्तर चतुर्भुज (Frequently Asked Questions Related to Parallelogram in Class 9th),समान्तर चतुर्भुज कक्षा 9 (Parallelogram Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.चतुर्भुज किसे कहते हैं? (What is a Quadrilateral?):
उत्तर:चार भुजाओं से घिरी हुई आकृति को चतुर्भुज कहते हैं।
प्रश्न:2.समान्तर चतुर्भुज के गुणधर्म लिखिए। (Write the Properties of Parallelogram):
उत्तर:(1.)समान्तर चतुर्भुज की सम्मुख भुजाएँ समान्तर होती हैं।
(2.)समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
(3.)समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती है।
(4.)समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
(5.)समान्तर चतुर्भुज की सम्मुख भुजाओं का युग्म परस्पर समान्तर और बराबर होता है।
(6.)समान्तर चतुर्भुज का विकर्ण इसे दो सर्वांगसम त्रिभुजों में बाँटता है।
प्रश्न:3.समलम्ब चतुर्भुज किसे कहते हैं? (What is a Trapezium Called?):
उत्तर:उस चतुर्भुज को समलम्ब चतुर्भुज (trapezium) कहते हैं जिसकी सम्मुख भुजाओं का एक युग्म परस्पर समान्तर हो।
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 9वीं में समान्तर चतुर्भुज (Parallelogram in Class 9th),समान्तर चतुर्भुज कक्षा 9 (Parallelogram Class 9) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Parallelogram in Class 9th
कक्षा 9वीं में समान्तर चतुर्भुज
(Parallelogram in Class 9th)
Parallelogram in Class 9th
कक्षा 9वीं में समान्तर चतुर्भुज (Parallelogram in Class 9th) के इस आर्टिकल में समान्तर चतुर्भुज
व उसके गुणधर्मों पर आधारित कुछ महत्त्वपूर्ण सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.