Irrational Numbers
1.अपरिमेय संख्याएँ (Irrational Numbers),अपरिमेय संख्याएँ परिभाषा (Irrational Numbers Definition):
एक अपरिमेय संख्या (Irrational Numbers) का दशमलव प्रसार अनवसानी अनावर्ती होता है।विलोमत: वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती (Non-terminating non-recuring) होता है,अपरिमेय होती है।
अतः अपरिमेय संख्याएँ (Irrational Numbers) वे होती है जिन्हें \frac{p}{q} के रूप में न लिखा जा सकता हो जहां p और q पूर्णांक है और q \neq 0 है।अपरिमेय संख्याएँ अपरिमित रूप से अनेक होती हैं जिसके कुछ उदाहरण निम्न है:
\sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7},\pi,0.150150015000150000….
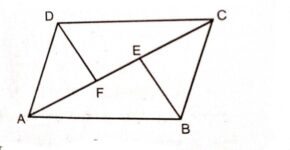
त्रिभुज \triangle ABC में AC^{2}=AB^{2}+BC^{2} \\ \Rightarrow AC^{2}=1^{2}+1^{2} \\ \Rightarrow AC =\sqrt{2}
यहाँ हमें शुल्व-नियम (पाइथागोरस प्रमेय) कर्ण के वर्ग का मान प्राप्त हुआ।लेकिन 2 का वर्गमूल क्या होगा?यदि 9,25,169 या अन्य किसी वर्ग संख्या का वर्गमूल पूछा जाता तो आसानी से उत्तर दिया जा सकता था क्योंकि इनका वर्गमूल क्रमश: 3,5 और 13 होगा।
दरअसल \sqrt{2} एक ऐसी लंबाई है जिसे स्केल से ठीक-ठीक मापा ही नहीं जा सकता है।इस विश्व की सारी वस्तुओं को मापने योग्य संख्याओं में व्यक्त नहीं किया जा सकता है।
जबकि पाइथागोरस की मान्यता थी कि इस विश्व की सभी संख्याओं को परिमेय संख्याओं में व्यक्त किया जा सकता है अर्थात् मापा जा सकता है। पाइथागोरस का ज्ञान परिमेय संख्या \frac{a}{b} के रूप में लिखी जा सकने वाली संख्याओं तक ही सीमित था।
लगभग 400 ईसवी पूर्व ग्रीस के प्रसिद्ध गणितज्ञ और दार्शनिक पाइथागोरस के अनुयायियों ने संभवत क्रोटोन के हिपाक्स ने इन अपरिमेय संख्याओं का पता लगाया था।इस खोज से पाइथागोरस की आंखें खुल गई।उसने जाना की विश्व में ऐसी भी वस्तुएँ (परिमाण) हैं जिन्हें परिमेय संख्याओं में व्यक्त नहीं किया जा सकता है।
पाइथागोरस ने इस नई खोज को बाहर के लोगों के सामने प्रकट नहीं होने दिया।उसने अपने शिष्यों को आदेश दे रखा था कि जो कोई इस खोज को बाहर प्रकट करेगा उसका बड़ा अहित होगा।लेकिन उसके शिष्य हिपाक्स ने इस रहस्य को बाहर प्रकट कर दिया जिसके कारण हिपाक्स का दुर्भाग्यपूर्ण अंत कर दिया गया।अंत में यूनान के विद्वानों को इसका पता चल गया।
सुप्रसिद्ध अपरिमेय संख्या \sqrt{2} और \pi के दशमलव प्रसार है:
\sqrt{2}=1.4142135623730950488016887242096…….
\pi=3.14159265358979323846264338327950…….
वर्षों से गणितज्ञों ने अपरिमेय संख्याओं के दशमलव प्रसार में अधिक से अधिक अंकों को उत्पन्न करने की विभिन्न तकनीक विकसित की है। उपर्युक्त का मान विभाजन विधि (Division Method) से ज्ञात किया जा सकता है।यह एक रोचक बात है कि सुल्ब-सूत्रों (जीवा-नियमों) में जो वैदिक युग (800 ईसा पूर्व-500 ईसा पूर्व) के गणितीय ग्रंथ हैं,हमें \sqrt{2} का एक सन्निकट मान प्राप्त होता है,जो यह है:
\sqrt{2}=1+\frac{1}{3}+\left ( \frac{1}{4} \times \frac{1}{3} \right )-\left ( \frac{1}{34} \times \frac{1}{4} \times\frac{1}{3} \right )=1.4142156
\pi का मान ज्ञात करना भी काफी रोचक रहा है।यूनान का प्रबुद्ध व्यक्ति आर्कमिडीज ही वह पहला व्यक्ति था जिसने \pi के दशमलव प्रसार में अंको को अभिकलित किया था।उसने यह दिखाया कि 3.140845<\pi<3.142857 होता है।आर्यभट (476-550 ईस्वी) ने जो एक महान भारतीय गणितज्ञ और खगोलविद् थे चार दशमलव स्थानों तक शुद्ध \pi का मान (3.1416) ज्ञात किया था।उच्च चाल कंप्यूटरों और उन्नत कलन विधियों (algorithms) का प्रयोग करके 1.24 ट्रिलियन से भी अधिक दशमलव स्थानों तक \pi का मान अभिकलित किया जा चुका है।
अपरिमेय संख्याएँ (Irrational Numbers) योग और गुणन के क्रमविनिमेय,साहचर्य और बंटन नियमों को संतुष्ट करती हैं।परंतु अपरिमेय संख्याओं के योग,अंतर,भागफल और गुणनफल सदा अपरिमेय नहीं होते हैं।उदाहरणार्थ:
\sqrt{2}-\sqrt{2},\sqrt{3}.\sqrt{3} और \frac{\sqrt{\pi}}{\sqrt{\pi}} अपरिमेय संख्याएँ (Irrational Numbers) हैं।
इसी प्रकार जब एक परिमेय संख्या में अपरिमेय संख्या जोड़ते हैं और एक अपरिमेय संख्या को एक परिमेय संख्या से गुणा करते हैं तो अपरिमेय संख्या प्राप्त होती है क्योंकि इन संख्याओं का भी अनवसानी अनावर्ती दशमलव प्रसार प्राप्त होता है।
उदाहरणार्थ:3+\sqrt{7} और 3 \sqrt{7}
प्रमेय (Theorem): मान लीजिए p एक अभाज्य संख्या है।यदि p,a^{2} को विभाजित करती है तो p,a को भी विभाजित करेगी जहां a एक धनात्मक पूर्णांक है।
उपपत्ति (Proof):मान लीजिए a के अभाज्य गुणनखंडन निम्नलिखित रूप के हैं: a=p_{1}p_{2}p_{3} \ldots p_{n} जहां p_{1}p_{2}p_{3} \ldots p_{n} अभाज्य संख्याएँ हैं परंतु आवश्यक रूप से भिन्न-भिन्न नहीं है।
अतः a^{2}=\left ( p_{1}p_{2}p_{3} \ldots p_{n} \right )\left ( p_{1}p_{2}p_{3} \ldots p_{n} \right ) \\ =p^{2}_{1}p^{2}_{2}p^{2}_{3} \ldots p^{2}_{n}
अब हमें दिया है किp,a^{2} को विभाजित करती है। इसलिए अंकगणित की आधारभूत प्रमेय के अनुसार;p, a^{2} का एक अभाज्य गुणनखंड है।परंतु अंकगणित की आधारभूत प्रमेय की अद्वितीयता के गुण का प्रयोग करने पर हम पाएंगे कि a^{2} के अभाज्य गुणनखंड केवल p_{1}p_{2}p_{3} \ldots p_{n} हैं।इसलिए p,a को विभाजित अवश्य करेगा।
अब हम इसकी उत्पत्ति दे सकते हैं कि \sqrt{2} एक अपरिमेय संख्या है।यह उपपत्ति इस तकनीक पर आधारित है जिसे ‘विरोधोक्ति द्वारा उपपत्ति (Proof by Contradiction)’कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Rational Numbers
2.अपरिमेय संख्याओं के उदाहरण (Irrational Numbers Examples):
Example:1.सिद्ध कीजिए कि \sqrt{5} एक अपरिमेय संख्या है।
Solution:उपपत्ति (Proof):हम इसके विपरीत यह मान लेते हैं कि \sqrt{5} एक परिमेय संख्या है।
अतः हम दो पूर्णांक a और b(\neq 0) प्राप्त कर सकते हैं कि \sqrt{5}=\frac{a}{b} है।
यदि a और b में,1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड हो तो उस उभयनिष्ठ गुणनखण्ड से भाग देकर a और b को सहअभाज्य बना सकते हैं।अतः b \sqrt{5}=a है।
दोनों पक्षों का वर्ग करने तथा पुनर्व्यवस्थित करने पर हमें 5 b^{2}=a^{2} प्राप्त होता है।
अतः a^{2},5 से विभाजित है।अतः 5,a को विभाजित करता है।
माना कि a=5c (c कोई पूर्णांक है)
\Rightarrow a^{2}=25c^{2} \\ \Rightarrow 5b^{2}=25c^{2}\left [ a^{2}=5b^{2} \right ] \\ \Rightarrow b^{2}=5c^{2}
अतः 5,b^{2} को विभाजित करता है।
\therefore 5,b को विभाजित करता है।
\because a भी 5 से विभाज्य है और b भी 5 से विभाज्य है।
\therefore 5,a और b का सार्वनिष्ठ अभाज्य गुणनखण्ड है (जो 1 के अतिरिक्त है)।
यह एक विरोधाभास है क्योंकि हमारी मान्यता के अनुसार a और b में (1 के अतिरिक्त) कोई अभाज्य गुणनखण्ड नहीं है।
हमें यह विरोधाभास अपनी त्रुटिपूर्ण कल्पना के कारण प्राप्त हुआ है कि \sqrt{5} एक परिमेय संख्या है
अतः हम निष्कर्ष निकालते हैं कि \sqrt{5} एक अपरिमेय संख्या है।
Example:2.सिद्ध कीजिए कि 3+2\sqrt{5} एक अपरिमेय संख्या है।
Solution:माना कि 3+2\sqrt{5} एक परिमेय संख्या है।
अर्थात् सहअभाज्य (Co-prime) संख्याएँ a और b (b \neq 0)प्राप्त कर सकते हैं कि
3+2\sqrt{5}=\frac{a}{b}
अतः 2\sqrt{5}=\frac{a}{b}-3
इस समीकरण को पुनर्व्यवस्थित करने पर:
\sqrt{5}=\frac{a}{2b}-\frac{3}{2}
चूँकि a और b पूर्णांक हैं इसलिए \frac{a}{2b}-\frac{3}{2} एक परिमेय संख्या है।
अर्थात् \sqrt{5} एक परिमेय संख्या है।
परन्तु इससे इस तथ्य का विरोधाभास प्राप्त होता है कि \sqrt{5} एक अपरिमेय संख्या है।
हमें यह विरोधाभास अपनी गलत कल्पना के कारण प्राप्त हुआ है कि 3+2\sqrt{5} एक परिमेय संख्या है।
अतः हम निष्कर्ष निकालते हैं कि 3+2\sqrt{5} एक अपरिमेय संख्या है।
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय है (प्रश्न 3 से 5)
Example:3.\frac{1}{\sqrt{2}}
Solution:माना \frac{1}{\sqrt{2}} परिमेय संख्या है।
अर्थात् हम सह-अभाज्य (Co-prime) संख्याएँ a और b(b \neq 0) ज्ञात कर सकते हैं कि
\frac{1}{\sqrt{2}}=\frac{a}{b}
दोनों पक्षों का वर्ग करने पर:
\left ( \frac{1}{\sqrt{2}} \right )^{2} =\left ( \frac{a}{b} \right )^{2} \\ \Rightarrow \frac{1}{2}=\frac{a^{2}}{b^{2}}
अतः b^{2},2 से भाज्य है।
\therefore b भी 2 से भाज्य है।
तब माना b=2c
\Rightarrow b^{2}=(2c)^{2} \\ \Rightarrow b^{2}=4c^{2}\left [\because b^{2}=2a^{2} \right ] \\ \Rightarrow a^{2}=2c^{2}
अतः a^{2} ,2 से भाज्य है।
\therefore a भी 2 से भाज्य है।
\therefore a और b दोनों 2 से भाज्य है।अतः a और b का (1 के अतिरिक्त) सार्वनिष्ठ अभाज्य गुणनखण्ड 2 है।
यह एक विरोधाभास है क्योंकि हमारी मान्यता के अनुसार a और b में (1 के अतिरिक्त) कोई अभाज्य गुणनखण्ड सार्वनिष्ठ नहीं है।
हमें यह विरोधाभास अपनी त्रुटिपूर्ण कल्पना के कारण प्राप्त हुआ है कि \frac{1}{\sqrt{2}} एक परिमेय संख्या है।
अतः हम निष्कर्ष निकालते हैं कि \frac{1}{\sqrt{2}} एक अपरिमेय संख्या है।
Example:4.7\sqrt{5}
Solution:माना 7\sqrt{5} एक परिमेय संख्या है।
अर्थात् हम सह-अभाज्य (Co-prime) संख्याएँ a और b(b \neq 0) प्राप्त कर सकते हैं कि
7\sqrt{5}=\frac{a}{b} \\ \Rightarrow \sqrt{5}=\frac{a}{7b}
a,b और 7 सभी पूर्णांक हैं।अतः \frac{a}{7b} एक परिमेय संख्या है।
फलतः \sqrt{5} भी एक परिमेय संख्या है।
इससे इस तथ्य का विरोधाभास प्राप्त होता है कि \sqrt{5} एक अपरिमेय संख्या है।
हमें यह विरोधाभास अपनी गलत कल्पना के कारण प्राप्त हुआ है कि 7\sqrt{5} एक परिमेय संख्या है।
अतः हम निष्कर्ष निकालते हैं कि 7\sqrt{5} एक अपरिमेय संख्या है।
Example:5. 6+\sqrt{2}
Solution:माना कि 6+\sqrt{2} एक परिमेय संख्या है।
हम ऐसे दो पूर्णांक a और b(b \neq 0) प्राप्त कर सकते हैं कि
6+\sqrt{2}=\frac{a}{b} \\ \Rightarrow \sqrt{2}=\frac{a}{b}-6 \\ \Rightarrow \sqrt{2}=\frac{a-6b}{b}
चूँकि 6,a,b पूर्णांक हैं अतः \frac{a-6b}{b} एक परिमेय संख्या है।
\therefore \sqrt{2} एक परिमेय संख्या है।
यह इस तथ्य का विरोधाभास है कि एक अपरिमेय संख्या है।
हमें यह विरोधाभास अपनी गलत कल्पना के कारण प्राप्त हुआ है कि 6+\sqrt{2} एक परिमेय संख्या है।
अतः हम निष्कर्ष निकालते हैं कि 6+\sqrt{2} एक अपरिमेय संख्या है।
Example:6.परिमेय संख्याओं \frac{5}{7} और \frac{9}{11} के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
Solution: \frac{5}{7}=0.714285714……
\frac{9}{11}=0.818181818……
अतः दोनों परिमेय संख्याओं के बीच तीन अपरिमेय संख्याएँ निम्न हैं:
0.73073007300073000073…..
0.75075007500075000075….
0.78078007800078000078….
इसी प्रकार की इन दोनों के बीच अपरिमित रूप से अनेक संख्याएँ ज्ञात कर सकते हैं।
उपर्युक्त उदाहरणों के द्वारा अपरिमेय संख्याएँ (Irrational Numbers),अपरिमेय संख्याएँ परिभाषा (Irrational Numbers Definition) को समझ सकते हैं।
3.अपरिमेय संख्याएँ के सवाल (Irrational Numbers Questions):
(1.)सिद्ध कीजिए कि \sqrt{3} एक अपरिमेय संख्या है।
(2.)दर्शाइए कि 5-\sqrt{3} एक अपरिमेय संख्या है।
(3.)\frac{1}{7} और \frac{2}{7} के बीच की एक अपरिमेय संख्या ज्ञात कीजिए।
उत्तर (Answer):
उपर्युक्त सवालों को हल करने पर अपरिमेय संख्याएँ (Irrational Numbers),अपरिमेय संख्याएँ परिभाषा (Irrational Numbers Definition) को ठीक से समझ सकते हैं।
(3.)0.150150015000150000…
Also Read This Article:-Mode of Grouped Data
4.अपरिमेय संख्याएँ (Irrational Numbers),अपरिमेय संख्याएँ परिभाषा (Irrational Numbers Definition) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.अपरिमेय संख्या उदाहरण क्या है? (What is irrational number example?):
उत्तर:एक उदाहरण दीजिए।एक अपरिमेय संख्या वास्तविक संख्या का एक प्रकार है जिसे एक साधारण भिन्न के रूप में दर्शाया नहीं जा सकता है। इसे अनुपात के रूप में व्यक्त नहीं किया जा सकता है।उदाहरण: √2, √3, √5, √11, √21,π(Pi) सभी अपरिमेय हैं।
प्रश्न:2.क्या एक अपरिमेय संख्या माना जाता है? (What is considered an irrational number?):
उत्तर:अपरिमेय संख्या,कोई भी वास्तविक संख्या जिसे दो पूर्णांक के भागफल (Quotient of two integers) के रूप में व्यक्त नहीं किया जा सकता है।उदाहरण के लिए, पूर्णांक और भिन्नों के बीच कोई संख्या नहीं है जो 2 के वर्गमूल के बराबर होती है।
इस प्रकार यह आवश्यक हो गया, गणित के इतिहास में जल्दी,संख्या की अवधारणा का विस्तार करने के लिए अपरिमेय संख्या शामिल हैं ।
प्रश्न:3.वास्तविक नंबर क्या है? (What is real number?):
उत्तर:वास्तविक संख्या संख्या है जिसमें दोनों परिमेय और अपरिमेय संख्या शामिल हैं।जैसे परिमेय संख्याएँ पूर्णांक (-2, 0, 1),भिन्नें (\frac{1}{2}, 2.5) और अपरिमेय संख्या जैसे √3, π (\frac{22}{7}) आदि सभी वास्तविक संख्या हैं।
प्रश्न:4.आप कैसे जानते हैं कि इसके परिमेय या अपरिमेय हैं? (How do you know if its rational or irrational?):
उत्तर:जवाब-अगर कोई नंबर लिखा जा सकता है या \frac{p}{q} फॉर्म में बदला जा सकता है,जहां p और q पूर्णांक है और q नॉन जीरो नंबर है तो इसे परिमेय कहा जाता है और अगर इसे इस फॉर्म में नहीं लिखा जा सकता है तो यह अपरिमेय है।
प्रश्न:5.क्या 5.676677666777 एक तर्कसंगत संख्या है? (Is 5.676677666777 a rational number?):
उत्तर:हां,क्योंकि सभी पूर्णांक दशमलव होते हैं। नहीं,क्योंकि पूर्णांक में दशमलव नहीं होता है। … जेरेमी (Jeremy) का कहना है कि 5.676677666777. एक परिमेय संख्या है क्योंकि यह एक दशमलव है जो एक पैटर्न के साथ हमेशा के लिए चला जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा अपरिमेय संख्याएँ (Irrational Numbers),अपरिमेय संख्याएँ परिभाषा (Irrational Numbers Definition) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
Irrational Numbers
अपरिमेय संख्या (Irrational Numbers)
Irrational Numbers
एक अपरिमेय संख्या (Irrational Numbers) का दशमलव प्रसार अनवसानी अनावर्ती होता है।विलोमत: वह
संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती (Non-terminating non-recuring) होता है,अपरिमेय होती है।
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
