Properties of Parallelograms Diagonals
1.समांतर चतुर्भुज विकर्ण के गुणधर्म (Properties of Parallelograms Diagonals),समान्तर चतुर्भुज के गुणधर्म कक्षा 9 (Properties of Parallelogram Class 9)-
इस आर्टिकल में समांतर चतुर्भुज विकर्ण के गुणधर्मों (Properties of Parallelograms Diagonals) को कुछ प्रमेयों के माध्यम से समझने का प्रयत्न करेंगे।इससे पूर्व आर्टिकल में हमने समांतर चतुर्भुज की कुछ विशेष आकृतियों के बारे में बताया था।
प्रमेय (Theorem):1.यदि समान्तर चतुर्भुज के विकर्ण समान हों तो वह एक आयत होता है।
दिया है (Given):ABCD एक समान्तर चतुर्भुज है जिसमें AC=BD
सिद्ध करना है (To Prove):ABCD एक आयत है।
उपपत्ति (Proof): \triangle ABC और \triangle BAD में
BC=AD (स.च. की सम्मुख भुजाएं)
AB=AB (उभयनिष्ठ भुजा)
AC=BD (दिया है)
अतः भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle ABC \cong \triangle BAD
अतः सर्वांगसम त्रिभुजों के संगत कोण समान होंगे
अर्थात् \angle CBA= \angle DAB
परन्तु ये तिर्यक रेखा AB के एक ही ओर के अन्त:कोण हैं।
\angle DAB + \angle CBA=180° \\ \angle DAB = \angle CBA=90°
अतः ABCD एक आयत है।
प्रमेय (Theorem):2.(प्रमेय 1 का विलोम) एक आयत के विकर्ण परस्पर बराबर होते हैं।
दिया है (Given):ABCD एक आयत है।
सिद्ध करना है (To Prove):AC=BD
उपपत्ति (Proof): \triangle ABC तथा \triangle BAD में
AD=BC (आयत की सम्मुख भुजाएं बराबर होती है)
AB=AB (उभयनिष्ठ भुजा)
\angle ABC=\angle DAB=90°
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ABC \cong \triangle BAD
AC=BD (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
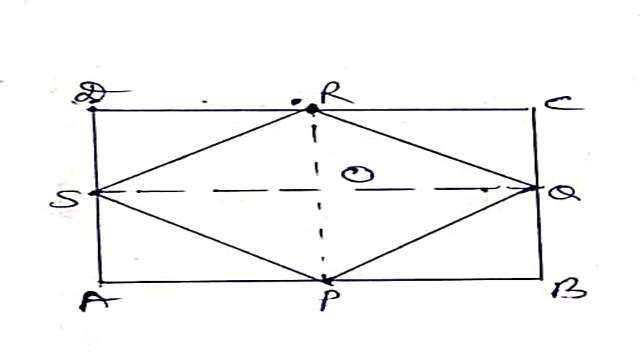
प्रमेय (Theorem):3.यदि समान्तर चतुर्भुज के विकर्ण परस्पर लम्बवत् हों तो वह एक समचतुर्भुज होता है।
दिया है (Given):समान्तर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर लम्बवत् हैं।
सिद्ध करना है (To Prove):ABCD एक समचतुर्भुज है।
उपपत्ति (Proof):\triangle AOB और \triangle COB में
OB=OB (उभयनिष्ठ भुजा)
\angle AOB=\angle BPC=90°(दिया है)
AO=CO (समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle AOB \cong \triangle COB
अतः सर्वांगसम त्रिभुजों की संगत भुजाएं समान होंगी।
अर्थात् AB=BC
अतः ABCD एक समचतुर्भुज है।
प्रमेय (Theorem):4.(प्रमेय:3 का विलोम) एक समचतुर्भुज के विकर्ण परस्पर लम्बवत् होते हैं।
दिया है (Given):ABCD एक समचतुर्भुज है।
सिद्ध करना है (To Prove):\angle AOB=\angle AOD=\angle BOC=\angle COD=90°
उपपत्ति (Proof): \triangle AOB तथा \triangle AOD में
AB=AD (समचतुर्भुज की भुजाएं समान होती हैं)
AO=AO (उभयनिष्ठ भुजा)
OB=OD (समचतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle AOB \cong \triangle AOD
\angle AOB=\angle AOD (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)…..(1)
\angle AOB+\angle AOD=180°(रैखिक कोण युग्म से)…..(2)
(1) व (2) से-
\angle AOB=\angle AOD=90°
इसी प्रकार \angle BOC=\angle COD=90°
अतः \angle AOB=\angle AOD=\angle BOC=\angle COD=90°
प्रमेय (Theorem):5.यदि एक समान्तर चतुर्भुज के विकर्ण परस्पर बराबर एवं लम्बवत् हो तो यह एक वर्ग होता है।
दिया है (Given):ABCD एक समान्तर चतुर्भुज है जिसमें AC=BD एवं AC \perp BD है।
सिद्ध करना है (To Prove):ABCD एक वर्ग है।
उपपत्ति (Proof): \triangle ABO और \triangle ADO में
BO=OD (ABCD एक समान्तर चतुर्भुज है)
\angle AOB=\angle AOD=90° (दिया है)
AO=AO (उभयनिष्ठ भुजा है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ABO \cong \triangle ADO
अतः सर्वांगसम त्रिभुजों की संगत भुजाएं समान होंगी।
अर्थात् AB=AD…..(1)
अब \triangle ABD और \triangle BAC में
BD=AC (दिया है)
AB=AB (उभयनिष्ठ भुजा)
AD=BC (सम्मुख भुजाएं)
अतः भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle ABD \cong \triangle BAC
अतः सर्वांगसम त्रिभुजों के संगत कोण समान होंगे
\angle DAB=\angle CBA......(2)
हम जानते हैं कि समान्तर चतुर्भुज के आसन्न कोणों का योग 180° होता है।
\angle DAB+\angle CBA=180°....(3)
(2) और (3) से-
\angle DAB=\angle CBA=90°.....(4)
(3) और (4) से-
ABCD एक वर्ग है।
प्रमेय (Theorem):6.(प्रमेय:5. की विलोम) एक वर्ग के विकर्ण बराबर और परस्पर लम्बवत् होते हैं।
दिया है (Given):ABCD एक वर्ग है।
सिद्ध करना है (To Prove):AC=BD तथा AC \perp BD
उपपत्ति (Proof): \triangle ABD और \triangle ABC में
AD=BC (वर्ग की भुजाएं)
AB=AB (उभयनिष्ठ भुजा है)
\angle DAB=\angle ABC=90°
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ABD \cong \triangle ABC
AC=BD (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
\triangle AOD तथा \triangle AOB में
AO=AO (उभयनिष्ठ भुजा है)
AB=AD (वर्ग की भुजाएं)
OD=OB (वर्ग के विकर्ण समद्विभाजित करते हैं)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle AOD \cong \triangle AOB \\ \angle AOD=\angle AOB....(2)
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\angle AOD+\angle AOB=180°(रैखिक कोण युग्म से)…..(3)
(2) एवं (3) से-
\angle AOD=\angle AOB......(4)
(1) तथा (4) से-
AC=BD तथा AC \perp BD
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Plane Geometry and Line and Angle
2.समांतर चतुर्भुज विकर्ण के गुणधर्म के उदाहरण (Properties of Parallelograms Diagonals Examples)-
Example-1.चित्र में ABCD और AEFG दो समान्तर चतुर्भुज हैं यदि \angle C=55° तो \angle F निर्धारित कीजिए।
Solution–
ABCD,AEFG समान्तर चतुर्भुज हैं अतः
\angle A= \angle C तथा \angle A= \angle F
(समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं)
अतः \angle F= \angle C \\ \angle F=55°
Example-2.क्या किसी चतुर्भुज के सभी कोण न्यून कोण हो सकते हैं? अपने उत्तर का कारण दीजिए।
Solution-किसी चतुर्भुज के सभी कोण न्यून कोण नहीं हो सकते हैं।क्योंकि चतुर्भुज के चारों कोणों का योग 360° होता है जो चार समकोण के बराबर होता है। इसलिए प्रत्येक कोण न्यून कोण होने पर चारों कोणों का योग 360° से कम हो जाएगा।
Example-3 क्या किसी चतुर्भुज के सभी कोण समकोण हो सकते हैं?अपने उत्तर का कारण दीजिए।
Solution-चतुर्भुज के सभी कोण समकोण हो सकते हैं।ऐसा चतुर्भुज आयत या वर्ग होगा।
Example-4.एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं।यदि \angle A=35° है तो \angle B निर्धारित कीजिए।
Solution-चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। अतः ABCD एक समान्तर चतुर्भुज है।
\angle A+\angle B=180°(समान्तर चतुर्भुज के आसन्न कोण)
\Rightarrow 35^{\circ} + \angle B=180^{\circ} \\ \Rightarrow \angle B=180^{\circ}-35^{\circ} \\ \Rightarrow \angle B =145^{\circ}
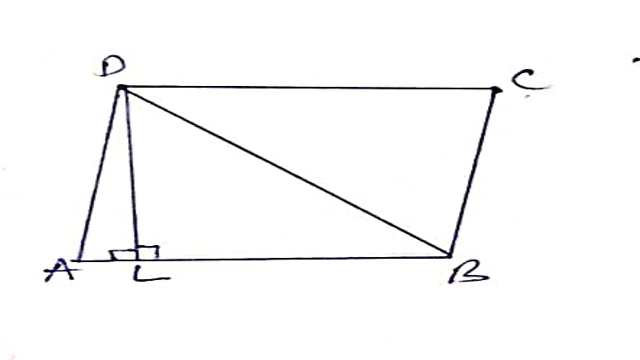
Example-5.ABCD एक समचतुर्भुज है जिसमें D से AB पर शीर्षलम्ब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
Solution–
\triangle ALD तथा \triangle BLD में
DL=DL (उभयनिष्ठ भुजा है)
\angle ALD =\angle BLD=90^{\circ}
AL=LB (दिया है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ALD \cong \triangle BLD \\ \angle A=\angle DBL.....(1)
(सर्वांगसम त्रिभुजों के संगत कोण)
\angle DBL=\angle CDB(एकान्तर कोण)….(2)
\angle A=\angle C (समचतुर्भुज के सम्मुख कोण)….(3)
(1) तथा (2) से-
\angle A=\angle CDB.....(4)
(3) तथा (4) से-
\angle C=\angle CDB
अतः BC=BD…..(5)
(बराबर कोण की अभिमुख भुजाएं बराबर होती है)
परन्तु BC=AD (समचतुर्भुज की भुजाएं बराबर होती है)…….(6)
(5) व (6) से-
AD=BD
अतः \triangle ABD में
AD=BD=AB
\therefore \angle A=60^{\circ} \\ \angle A +\angle ADC=180^{\circ} (समचतुर्भुज के आसन्न कोण)
60^{\circ} +\angle ADC=180^{\circ} \\ \Rightarrow \angle ADC=180^{\circ}-60^{\circ} \\ \Rightarrow \angle ADC=120^{\circ}
अतः समुचतुर्भुज के कोण
60°,120°,60°,120°
Example-6.एक समान्तर चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD पर क्रमशः बिन्दु P और Q इस प्रकार लिए गए हैं कि AP=CQ हैं।दर्शाइए कि AC और PQ परस्पर समद्विभाजित करते हैं।
Solution-दिया है (Given):ABCD एक समान्तर चतुर्भुज है।तथा AP=CQ
सिद्ध करना है (To Prove):OP=OQ,AO=OC
उपपत्ति (Proof):
\triangle AOP तथा \triangle COQ में
AP=CQ (दिया है)
\angle OAP= \angle OCQ(एकान्तर कोण)
\angle AOP= \angle COQ(सम्मुख कोण)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle AOP \cong \triangle COQ
OP=OQ,AO=CO
(सर्वांगसम त्रिभुजों की संगत भुजाएं समान होती है)
Example-7.चित्र में यह दिया है कि BDEF और FDCE समान्तर चतुर्भुज हैं।क्या आप कह सकते हैं कि BD=CD है?क्यों और क्यों नहीं?
Solution–
BDEF समान्तर चतुर्भुज है अतः
BD=EF …..(1)
(स.च. की सम्मुख भुजाएं समान होती है)
FDCE समान्तर चतुर्भुज है अतः
FE=CE …….(2)
(स.च. की सम्मुख भुजाएं समान होती है)
(1) व (2) से-
BD=CD
Example-8.सिद्ध कीजिए कि एक वर्ग की क्रमागत भुजाओं के मध्य बिन्दुओं को मिलाकर बनाया गया चतुर्भुज भी एक वर्ग होता है।
Solution-दिया है (Given):ABCD एक वर्ग है।P,Q,R,S वर्ग की भुजाओं क्रमशः AB,BC,CD,DA के मध्य बिन्दु हैं।
सिद्ध करना है (To Prove):PQRS एक वर्ग है।
उपपत्ति (Poof):
\triangle APS तथा \triangle RDS में
AP=DR (R व P मध्य बिन्दु हैं)
AS=SD (S,मध्य बिन्दु हैं)
\angle A=\angle D=90^{\circ}
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle APS \cong \triangle RDS
PS=SR ……(1)
इसी प्रकार सिद्ध कर सकते हैं कि
SP=PQ तथा PQ=QR …..(2)
(1) व (2) से-
PQ=QR=RS=OS ……(3)
त्रिभुज APS में
AP=AS
\angle APS=\angle ASP.....(4)
(बराबर भुजा के अभिमुख कोण बराबर होते हैं)
अतः \triangle APS में
\angle APS + \angle ASP+\angle A=180^{\circ} \\ \angle APS + \angle ASP+90^{\circ}=180^{\circ} \\ \angle APS + \angle ASP=90^{\circ}....(5)
(4) व (5) से-
\angle APS = \angle ASP=45^{\circ}....(6)
इसी प्रकार \angle DRS = \angle CRQ=\angle CQR=\angle BQP=\angle BPQ=45^{\circ}.....(7) \\ \angle APS +\angle SPQ+\angle BPQ=180^{\circ}(रैखिक कोण युग्म से)
\Rightarrow 45^{\circ}+45^{\circ}+\angle SPQ=180^{\circ} \\ \Rightarrow \angle SPQ=90^{\circ}....(8)
इसी प्रकार सिद्ध कर सकते हैं कि
\angle PQR=\angle QRS=\angle PSR=90^{\circ}....(9)
(8) व (9) से-
\angle PQR=\angle QRS=\angle PSR=\angle SPQ=90^{\circ}....(10)
(3) तथा (10) से-
PQRS एक वर्ग है।
Example-9.सिद्ध कीजिए कि एक आयत की भुजाओं के युग्मों के मध्य बिन्दुओं को मिलाने से एक समचतुर्भुज बनता है।
Solution-दिया है (Given):ABCD एक आयत है।तथा P,Q,R,S क्रमशः AB,BC,CD,DA के मध्य बिन्दु हैं।
सिद्ध करना है (To Prove):PQRS एक समचतुर्भुज है।
उपपत्ति (Proof):
\triangle APS तथा \triangle DRS में
AS=SD (S,AD का मध्य बिन्दु है)
\angle A=\angle D=90^{\circ}
AP=DR (P व R बराबर भुजाओं के मध्य बिन्दु हैं)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle APS \cong \triangle DRS
SP=SR….(1)
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती हैं)
इसी प्रकार सिद्ध कर सकते हैं कि
SP=PQ=QR ……(2)
(1) व (2) से-
SP=PQ=QR=RS ……(3)
चतुर्भुज SORD,APOS,PBQO,QCRO आयत हैं।अतः
\angle D=\angle SOR=90^{\circ} \\ \angle B=\angle POQ=90^{\circ} \\ \angle C=\angle QOR=90^{\circ} \\ \angle A=\angle POS=90^{\circ}
अतः \angle SOR=\angle POQ=\angle QOR=\angle POS=90^{\circ}....(4)
(3) व (4) से-
PQRS एक समचतुर्भुज है।
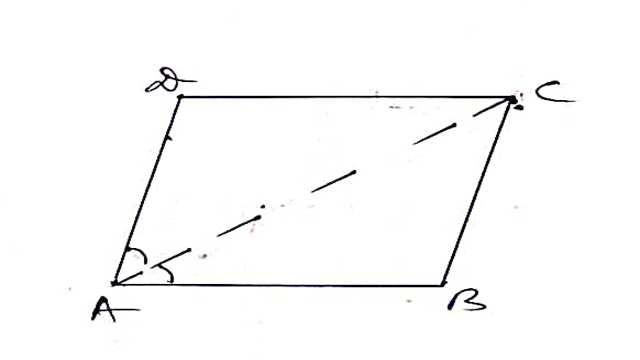
Example-10.एक समान्तर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। सिद्ध कीजिए कि यह समान्तर चतुर्भुज एक समचतुर्भुज है।
Solution-दिया है (Given): ABCD एक समान्तर चतुर्भुज है तथा \angle BAC=\angle DAC
सिद्ध करना है (To Prove):ABCD एक समचतुर्भुज है।
उपपत्ति (Proof):
\triangle ABC तथा \triangle ADC में
AC=AC (उभयनिष्ठ भुजा है)
\angle BAC=\angle DAC (दिया है)
\angle B=\angle D (स.च. के सम्मुख कोण)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ABC \cong \triangle ADC
\angle ACD=\angle BCA (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
परन्तु \angle A=\angle C (स.च. के सम्मुख कोण)
\frac{1}{2} \angle A=\frac{1}{2} \angle C \\ \angle CAD=\angle ACD
अतःAC=CD …….(1)
(बराबर कोण की अभिमुख भुजाएं बराबर होती है)
अतः इसी प्रकार AB=BC . …..(2)
(2) व (2) से-
AB=BC=CD=DA
अतः ABCD एक समचतुर्भुज है।
Example-11.P और Q क्रमशः एक समान्तर चतुर्भुज ABCD की सम्मुख भुजाएं AD और BC भुजाओं पर स्थित बिन्दु इस प्रकार है कि PQ विकर्ण AC और BD के प्रतिच्छेद बिन्दु O से होकर जाता है।सिद्ध कीजिए कि PQ बिन्दु O पर समद्विभाजित होता है।
Solution-दिया है (Given):ABCD एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):OP=OQ
उपपत्ति (Proof):
\triangle AOP तथा \triangle COQ में
AO=OC (स.च. के विकर्ण समद्विभाजित होते हैं)
\angle AOP=\angle COQ (सम्मुख कोण)
\angle OAP=\angle OCQ (एकान्तर कोण)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle AOP \cong \triangle COQ
OP=OQ
(सर्वांगसम त्रिभुजों की संगत भुजाएं समान होती है)
Example-12.ABCD एक आयत है जिसका विकर्ण BD, \angle B को समद्विभाजित करता है।दर्शाइए कि ABCD एक वर्ग है।
Solution-दिया है (Given):ABCD एक आयत है तथा \angle ABD=\angle CBD
सिद्ध करना है (To Prove):ABCD एक वर्ग है अर्थात् AB=BC=CD=DA
उपपत्ति (Proof):
\triangle ABD तथा \triangle BCD में
AB=CD (आयत की भुजाएं)
\angle ABD=\angle CBD (दिया है)
BD=BD (उभयनिष्ठ भुजा है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle ABD \cong \triangle BCD
\angle ADB=\angle CDB (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
अतः AB=AD (बराबर कोण की अभिमुख भुजाएं बराबर होती है)
अतः ABCD एक वर्ग है।
उपर्युक्त उदाहरणों के द्वारा समांतर चतुर्भुज विकर्ण के गुणधर्म (Properties of Parallelograms Diagonals) को समझ सकते हैं।
3.समांतर चतुर्भुज विकर्ण के गुणधर्म की समस्याएं (Properties of Parallelograms Diagonals Problems)-
(1.)एक समान्तर चतुर्भुज ABCD के सम्मुख कोण बराबर हैं।यदि AB=4 cm है तो CD निर्धारित करो।
(2.)ABCD एक समान्तर चतुर्भुज है।यदि इसके विकर्ण बराबर हैं तो \angle ABC का मान ज्ञात कीजिए।
(3.)एक समचतुर्भुज के विकर्ण परस्पर बराबर और लम्ब होते हैं।क्या यह कथन सत्य है।अपने उत्तर के लिए कारण दीजिए।
उत्तर (Answers):(1.)CD=4 cm (2.) 90°,यह चतुर्भुज एक आयत है।(3.)यह कथन असत्य है क्योंकि समचतुर्भुज के विकर्ण परस्पर लम्ब होते हैं परन्तु बराबर नहीं होते हैं।
उपर्युक्त सवालों को हल करने पर समांतर चतुर्भुज विकर्ण के गुणधर्म (Properties of Parallelograms Diagonals) को ठीक से समझ सकते हैं।
Also Read This Article:-Properties of Parallelogram
4.समांतर चतुर्भुज विकर्ण के गुणधर्म (Properties of Parallelograms Diagonals Problems) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.समान्तर चतुर्भुज के विकर्ण के गुणधर्म क्या हैं? (What are the Properties of the Diagonals of a Parallelogram?)
उत्तर-विकर्ण एक दूसरे को काटते हैं।विपरीत भुजाओं की एक जोड़ी लंबाई में समानांतर और बराबर होती है।आसन्न कोण सम्पूरक हैं।प्रत्येक विकर्ण चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है।विकर्ण लम्बाई में बराबर होते हैं।विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
क्षेत्रफल: b × h (base × height);
गुण: उत्तल
प्रश्न:2.क्या समान्तर चतुर्भुज के विकर्ण समान होते हैं? (Are Diagonals of Parallelogram Equal?)
उत्तर-समान्तर चतुर्भुज के विकर्ण लम्बाई में बराबर होते हैं।विकर्ण परस्पर समद्विभाजित करते हैं।
प्रश्न:3.क्या समान्तर चतुर्भुज के विकर्ण 90° पर समद्विभाजित करते हैं? (Does Diagonals of Parallelogram Bisect at 90?)
उत्तर-अब, विकर्णों को एक दूसरे को समकोण पर मोड़ने के लिए, अर्थात =∠AOD =∠COB =90° के लिए, दोनों त्रिभुजों में अन्य दो आंतरिक कोणों का योग 90∘ के बराबर होना चाहिए।इसलिए, एक समांतर चतुर्भुज के विकर्ण एक दूसरे को काटते हैं लेकिन जरूरी नहीं कि समकोण पर हो।इस प्रकार, दिया गया कथन गलत है।
प्रश्न:4.समान्तर चतुर्भुज के 7 गुणधर्म क्या हैं? (What are the 7 Properties of a Parallelogram?),समान्तर चतुर्भुज के 6 गुणधर्म (6 Properties of Parallelogram) विपरीत भुजाएं सर्वांगसम होते हैं(AB = DC)।
उत्तर-विपरीत कोण बराबर होते हैं (∠D =∠B) हैं।
आसन्न कोण सम्पूरक हैं (∠A + ∠D = 180°)।
यदि एक कोण समकोण है, तो सभी कोण समकोण हैं।
एक समांतर चतुर्भुज के विकर्ण एक दूसरे को काटते तथा समद्विभाजित करते हैं।
समांतर चतुर्भुज का प्रत्येक विकर्ण इसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
प्रश्न:5.क्या समान्तर चतुर्भुज के विकर्ण सर्वांगसम होते हैं? (Are the Diagonals of a Parallelogram Congruent?)
उत्तर-एक समांतर चतुर्भुज के विकर्ण कभी-कभी सर्वांगसम होते हैं।एक समचतुर्भुज के विकर्ण हमेशा लंबवत होते हैं। समांतर चतुर्भुज के आसन्न कोण कभी भी पूरक नहीं होते हैं।एक वर्ग हमेशा एक समचतुर्भुज होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा समांतर चतुर्भुज विकर्ण के गुणधर्म (Properties of Parallelograms Diagonals) को समझ सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा समांतर चतुर्भुज विकर्ण के गुणधर्म (Properties of Parallelograms Diagonals) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
