Tangent to Circle Class 10
1.वृत्त की स्पर्श रेखा कक्षा 10 (Tangent to Circle Class 10),एक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या (Number of Tangents from a Point on a Circle):
वृत्त की स्पर्श रेखा कक्षा 10 (Tangent to Circle Class 10) के इस आर्टिकल में एक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या तथा स्पर्श रेखा की लम्बाई का अध्ययन करेंगे।
प्रमेय (Theorem):10.2.दिया है (Given):वृत्त का केन्द्र O है और बाह्य बिन्दु P से दो स्पर्श रेखाएँ PQ और PR हैं।
सिद्ध करना है (To Prove):PQ=PR
रचना (Construction):OQ, OR व OP को मिलाया।
उपपत्ति (Proof):हम जानते हैं कि स्पर्श रेखा,वृत्त की त्रिज्या पर लम्बवत होती है अतः
\angle OQP=\angle ORP=90^{\circ} \cdots(1)
अब \triangle OQP तथा \triangle ORP में
\angle OQP=\angle ORP=90^{\circ}[(1) से]
OP=OP (उभयनिष्ठ भुजा)
OQ=OR (वृत्त की त्रिज्याएँ)
(समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से)
\triangle OQP \cong \triangle ORP
PQ=PR (CPCT)
टिप्पणी (Note):(1.) प्रमेय को पाइथागोरस प्रमेय का प्रयोग करके भी निम्न प्रकार सिद्ध किया जा सकता हैः
PQ^2=O P^2-O Q^2=O P^2-O R^2=P R^2 (क्योंकि OQ=OR)
जिससे प्राप्त होता है कि PQ=PR
(2.)यह भी ध्यान दीजिये कि \angle OPQ=\angle OPR।अतः OP कोण QPR का अर्धक है अर्थात् वृत्त का केन्द्र स्पर्श रेखाओं के बीच के कोण अर्धक पर स्थित होता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Tangent to a Circle Class 10
2.वृत्त की स्पर्श रेखा कक्षा 10 के साधित उदाहरण (Tangent to Circle Class 10 Solved Examples):
प्रश्न संख्या 1,2,3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।
Example:1.एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24cm तथा Q की केन्द्र से दूरी 25cm है।वृत्त की त्रिज्या हैः
(A)7cm (B)12cm (C)15cm (D)24.5cm
Solution:एक वृत्त जिसका केन्द्र O है।बाह्य बिन्दु Q से स्पर्श रेखा PQ की लम्बाई 24 सेमी तथा Q की केन्द्र से दूरी 25 सेमी है।
\angle QPO=90^{\circ}
समकोण \triangle QPO में
OQ^2=P Q^2+O P^2 \\ \Rightarrow(25)^2=(24)^2+O P^2 \\ \Rightarrow O P^2=(25)^2-(24)^2 \\ \Rightarrow O P^2=625-576 \\ \Rightarrow O P^2=49 \\ \Rightarrow O P=\sqrt{49} \\ \Rightarrow O P=7
अतः सही विकल्प (A) है।
Example:2.आकृति में यदि TP,TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि \angle PQQ=110^{\circ} तो \angle PTQ बराबर हैः
(A) 60° (B) 70° (C) 80° (D) 90°
Solution:स्पर्श रेखा त्रिज्या पर लम्बवत होती है।
\therefore \angle O P T=\angle O Q T=90^{\circ}
अतः चतुर्भुज POQT में
\angle OPT+\angle P O Q+\angle O Q T=\angle P T Q=360^{\circ} \\ \Rightarrow 90^{\circ}+ 110^{\circ}+ 90^{\circ}+\angle P T Q=360^{\circ} \\ \Rightarrow 290^{\circ}+\angle P T Q=360^{\circ} \\ \Rightarrow \angle P T Q=360^{\circ}-290^{\circ} \\ \Rightarrow \angle P T Q=70^{\circ}
अतः सही विकल्प (B) है।
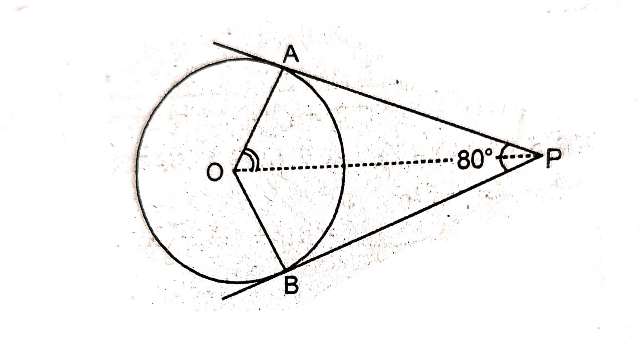
Example:3.यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हुई हों तो \angle POA बराबर हैः
(A) 50° (B) 60° (C) 70° (D) 80°
Solution:वृत्त का केन्द्र O है और बिन्दु P से PA व PB वृत्त पर स्पर्श रेखाएँ हैं जिनके बीच \angle A P B=80^{\circ} हैं।
OA व OB वृत्त त्रिज्या हैं
\angle A=90^{\circ} \text { और } \angle B=90^{\circ} \\ \therefore \angle AOB \text { व } \angle APB सम्पूरक कोण हैं।
\because \therefore \angle A O B+\angle A P B=180^{\circ} \\ \angle A O B=180^{\circ}-\angle A C \\ =180-80^{\circ} \\ \Rightarrow \angle A O B=100^{\circ}
हम जानते हैं कि OP रेखा को समद्विभाजित करती है।
\angle POA=\frac{1}{2} \angle A O B \\=\frac{1}{2} \times 10^{\circ} \\=50^{\circ} \\ \Rightarrow \angle POA=50^{\circ}
अतः सही विकल्प (A) है।
Example:4.सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
Solution:दिया है (Given):एक वृत्त जिसका केन्द्र O तथा व्यास AB है।PQ और RS बिन्दु A व B पर स्पर्श रेखाएँ हैं।
सिद्ध करना है (To Prove): PQ \parallel RS
उपपत्ति (Proof):OA त्रिज्या और PQ स्पर्श रेखा, OA त्रिज्या पर लम्ब है।
\angle 1=90^{\circ}
इसी प्रकार RS \perp OB \\ \angle 2=90^{\circ}
अब \angle 1=\angle 2
परन्तु यह दो समान्तर रेखाओं के एकान्तर कोण हैं जब एक तिर्यक रेखा उन्हें काटती है।
PQ \parallel RS
अतः किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समान्तर होती हैं।
Example:5.सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
Solution:दिया है (Given):एक वृत्त जिसका केन्द्र O है।AB उसकी स्पर्श रेखा है जो वृत्त को P पर स्पर्श करती है।
P से वृत्त की स्पर्श रेखा AB पर PQ लम्ब खींचा।
सिद्ध करना है (To Prove):लम्ब PQ वृत्त के केन्द्र O से जाता है।
उपपत्ति (Proof):स्पर्श रेखा AB वृत्त की त्रिज्या पर लम्ब होती है।
\therefore P Q \perp A B \\ P Q \perp A P
PQ रेखा में वृत्त की त्रिज्या समाहित होगी।
त्रिज्या का एक सिरा P है तथा दूसरा सिरा वृत्त के केन्द्र O पर होगा।
अतः लम्ब PQ वृत्त के केन्द्र O से होकर जाता है।
Example:6.एक बिन्दु A से जो एक वृत्त के केन्द्र से 5cm दूरी है, वृत्त पर स्पर्श रेखा की लम्बाई 4cm है।वृत्त की त्रिज्या ज्ञात कीजिए।
Solution:एक वृत्त जिसका केन्द्र O है।वृत्त के बाहर इसका केन्द्र से 5 सेमी की दूरी पर कोई बिन्दु A है।
स्पर्श रेखा की लम्बाई=PA=4 सेमी
वृत्त पर स्पर्श रेखा PA, त्रिज्या OP पर लम्ब है।
\angle OPA=90^{\circ}
अब समकोण \triangle OPA में पाइथागोरस प्रमेय का प्रयोग करने परः
O A^2=O P^2+P A^2 \\ \Rightarrow O P^2 =O A^2-P A^2 \\ =(5)^2-(4)^2 \\ =25-16 \\ =9 \\ \Rightarrow O P =\sqrt{9} \\ \Rightarrow O P =3 सेमी
अतः वृत्त की त्रिज्या 3 सेमी है।
Example:7.दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5cm तथा 3cm हैं।बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
Solution:माना O केन्द्र वाले दो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ OA तथा OP क्रमशः 5 सेमी व 3 सेमी हैं।
बड़े वृत्त की एक जीवा AB है जो छोटे वृत्त को बिन्दु P पर स्पर्श करती है।
त्रिज्या Q P \perp A B \\ \angle O P A=90^{\circ}
समकोण में पाइथागोरस प्रमेय सेः
A P^2+O P^2=O A^2 \\ \Rightarrow A P^2+(3)^2=(5)^2 \\ \Rightarrow A P^2=(5)^2-(3)^2 \\= 25-9 \\ \Rightarrow A P^2 =16 \\ \Rightarrow A P =\sqrt{16} \\ \Rightarrow A P=4 सेमी
परन्तु बड़े वृत्त में जीवा AB पर केन्द्र O से OP लम्ब है।
बिन्दु P, जीवा AB को समद्विभाजित करता है।
AP=BP=4 सेमी
जीवा AB की लम्बाई=AP+BP=4+4=8 सेमी
अतः बड़े वृत्त की जीवा की लम्बाई=8 सेमी
Example:8.एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है (देखिए आकृति)।सिद्ध कीजिए AB+CD=AD+BC
Solution:दिया है (Given):O केन्द्र वाले वृत्त के परिगत एक चतुर्भुज ABCD खींचा जिसकी भुजाएँ AB, BC, CD और DA वृत्त को क्रमशः बिन्दुओं P, Q, R और S पर स्पर्श करती है।
सिद्ध करना है (To Prove):AB+CD=AD+BC
उपपत्ति (Proof):किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई बराबर होती है।
अब B वृत्त के बाहर स्थित कोई बिन्दु है और BP,BQ वृत्त पर स्पर्श रेखाएँ हैं।
BP=BQ …. (1)
इसी प्रकार AP=AS …. (2)
और DR=DS ….. (3)
साथ ही CR=CQ ….. (4)
समीकरण (1),(2),(3) व (4) को जोड़ने परः
BP+AP+DR+CR=BQ+AS+DS+CQ
(AP+BP) +(CR+DR)=(AS+DS)+(BQ+CQ)
AB+CD=AD+BC
Example:9.आकृति में XY तथा X’Y’,O केन्द्र वाले किसी वृत्त पर दो समान्तर रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्शरेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है।सिद्ध कीजिए कि \angle AOB=90^{\circ} है।
Solution:दिया है (Given):XY तथा X’Y’ केन्द्र O वाले वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर एक अन्य स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है।OA तथा OB को मिलाया।
सिद्ध करना है (To Prove):\angle AOB=90^{\circ}
रचना (Construction):OC को मिलाया।
उपपत्ति (Proof):XY और X’Y’ वृत्त की दो स्पर्श रेखाएँ हैं जो वृत्त को P और Q पर स्पर्श करती हैं।बिन्दु C से वृत्त की स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर काटती है।
बिन्दु A से वृत्त पर AP व AC स्पर्श रेखाएँ हैं।
\triangle OPA तथा \triangle O C A में
OP=OC (वृत्त की त्रिज्याएँ)
AP=AC (बाह्य बिन्दु से वृत्त की स्पर्श रेखाएँ)
OA=OA (उभयनिष्ठ भुजा)
\therefore \triangle OPA \cong \triangle OCA
सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं।
\angle POA=\angle AOC \ldots (1)
इसी प्रकार बिन्दु B से वृत्त पर BQ और BC स्पर्श रेखाएँ हैं।
\triangle OQB तथा \triangle O B C में
OQ=OC (वृत्त की त्रिज्याएँ)
BQ=BC (बिन्दु B से वृत्त पर स्पर्श रेखाएँ)
OB=OB (उभयनिष्ठ भुजा)
\therefore \triangle OQB \cong \triangle OBC \\ \Rightarrow \angle BOQ=\angle COB \cdots(2)
अब \angle POA+ \angle A O C+\angle C O B+\angle B O Q=180^{\circ}
समीकरण (1) व (2) सेः
\Rightarrow \angle A O C+\angle A O C+\angle C O B+\angle C O B=180^{\circ} \\ \Rightarrow 2(\angle A O C+\angle C O B)=180^{\circ} \\ \Rightarrow \angle A O C+\angle O B=\frac{180^{\circ}}{2} \\ \Rightarrow \angle A O C+\angle C O B=90^{\circ} \\ \Rightarrow \angle A O B=90^{\circ}
Example:10.सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक कोण होता है।
Solution:दिया है (Given):एक वृत्त जिसका केन्द्र O है।P वृत्त के बाहर स्थित किसी बिन्दु P से PQ और PR दिए गए वृत्त पर स्पर्श रेखाएँ हैं।
सिद्ध करना है (To Prove): \angle R O Q+\angle Q P R=180^{\circ}
उपपत्ति (Proof):OQ त्रिज्या है तथा बिन्दु P से PQ स्पर्श रेखा है जो वृत्त को बिन्दु Q पर स्पर्श करती है।
\angle OQP=90^{\circ} [वृत्त के किसी बिन्दु पर स्पर्श रेखा वृत्त की त्रिज्या पर लम्ब होती है]
इसी प्रकार \angle ORP=90^{\circ}
अब चतुर्भुज ROQP में
\angle R O Q+\angle P R O+\angle O Q P+\angle Q P R=360^{\circ} \\ \Rightarrow \angle R O Q+90^{\circ}+90^{\circ}+\angle Q P R=360^{\circ} \\ \Rightarrow \angle ROQ+\angle QPR= 360^{\circ}-180^{\circ} \\ \angle ROQ+\angle QPR=180^{\circ}
अतः \angle QPR, \angle ROQ का सम्पूरक है।
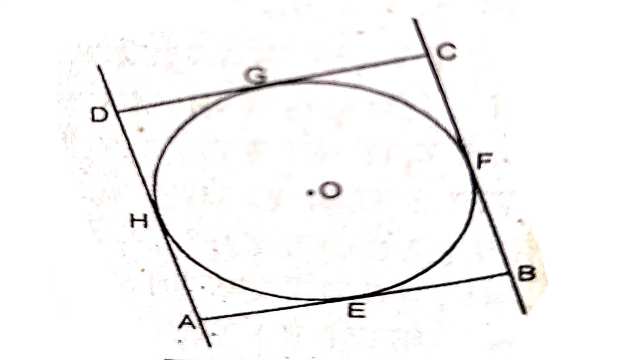
Example:11.सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है।
Solution:दिया है (Given):केन्द्र O वाले वृत्त के परिगत एक समान्तर चतुर्भुज ABCD खींचा जिसकी भुजाएँ वृत्त को क्रमशः E, F, G व H बिन्दुओं पर स्पर्श करती हैं।
सिद्ध करना है (To Prove):ABCD एक समचतुर्भुज है।
उपपत्ति (Proof):बाहरी बिन्दु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लम्बाई समान होती है।
अब वृत्त के बाहर स्थित बिन्दु B से BE और BF वृत्त पर दो स्पर्श रेखाएँ हैं।
BE=BF ….. (1)
इसी प्रकार AE=AH …. (2)
CG=CF …… (3)
तथा DG=DH …. (4)
समीकरण (1),(2),(3) व (4) को जोड़ने परः
(BE+AE)+(CG+DG)=(BF+CF)+(AH+DH)
AB+CD=BC+AD …. (5)
दिया है ABCD एक समान्तर चतुर्भुज है।
AB=CD तथा BC=AD ….. (6)
समीकरण (5) व (6) सेः
AB+AB=BC+BC
2AB=2BC
AB=BC
AB=BC=CD=AD
अतः ABCD एक समचतुर्भुज है।
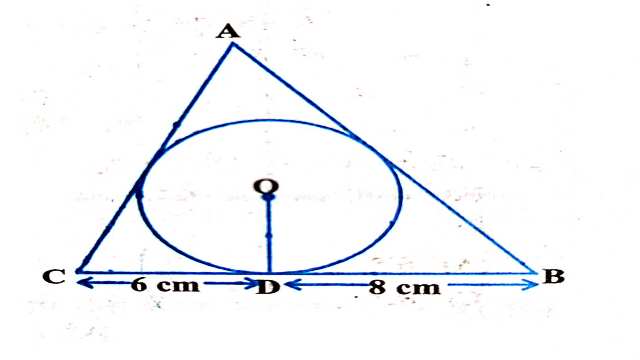
Example:12.4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिसमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाईयाँ क्रमशः 8cm और 6cm हैं (देखिए आकृति)।भुजाएँ AB तथा AC ज्ञात कीजिए।
Solution:4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक खींचा गया है।त्रिभुज की भुजाएँ BC, CA, AB वृत्त को क्रमशः D,E व F बिन्दुओं पर स्पर्श करती है।
किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई समान होती है।
AE=AF=x सेमी (माना)
CE=CD=6 सेमी और BF=BD=8 सेमी
वृत्त की स्पर्श रेखा,त्रिज्या पर लम्ब होती है।
\therefore O D \perp BC, O E \perp A C \text { और } OF \perp A B
\triangle ABC में b=AC=(x+6) सेमी
a=CB=(6+8) सेमी=14 सेमी
c=BA=(8+x) सेमी
अर्ध परिमाप (S)=\frac{a+b+c}{2} \\ \Rightarrow S=\frac{14+x+6+8+x}{2}=\frac{2 x+28}{2} \\ \Rightarrow S=x+14 \\ \triangle ABC का क्षेत्रफल
=\sqrt{S(S-a)(S-b)(S-c)} \\ =\sqrt{(x+14)(x+14-14)[(x+14)-(x+6)]\times[x+14-(8+x)]} \\ =\sqrt{(x+14) \times x \times 8 \times 6} \\ =\sqrt{48 x^2+672 x} सेमी ….(1)
\triangle OBC का क्षेत्रफल=\frac{1}{2} \times \text { आधार } \times \text { ऊचाई } \\ =\frac{1}{2} \times 14 \times 4=28 \text{ सेमी }^{2} \cdots(2) \\ \triangle BOA का क्षेत्रफल=\frac{1}{2} \times(8+x) \times 4=(16+2 x) \cdots(3) \\ \triangle AOC का क्षेत्रफल=\frac{1}{2} \times(6+x) \times 4=(12+2 x) \cdots(4) \\ \triangle ABC का क्षेत्रफल=\triangle OBC का क्षेत्रफल+\triangle BOA का क्षेत्रफल+ \triangle AOC का क्षेत्रफल
\sqrt{\left(48 x^2+672 x\right)}=28+16+2 x+12+2 x \\ \Rightarrow \sqrt{48 x^2+672 x}=4 x+56 \\ \Rightarrow \sqrt{\left(48 x^2+672 x\right)}=4(x+14)
दोनों पक्षों का वर्ग करने परः
\Rightarrow 48 x^2+672 x=16(x+14)^2 \\ \Rightarrow 48 x(x+14)=16(x+14)^2 \\ \Rightarrow 3 x=x+14 \Rightarrow x=7
AC=x+6=7+6=13 सेमी
AB=x+8=7+8=15 सेमी
Example:13.सिद्ध कीजिए कि परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
Solution:दिया है (Given):केन्द्र O वाले वृत्त के परिगत बना चतुर्भुज PQRS जिसकी भुजाएँ PQ,QR,RS और SP को क्रमशः L, M,N,T बिन्दुओं पर स्पर्श करती है।
सिद्ध करना है (To Prove): \angle POQ+\angle SOR=180^{\circ}
और \angle S O P+\angle R O Q=180^{\circ}
रचना (Construction):वृत्त के केन्द्र O से P,Q,R,S,L,M,N तथा T को मिलाया।
उपपत्ति (Proof):बाह्य बिन्दु से किसी वृत्त पर खींची गई दो स्पर्श रेखाएँ केन्द्र पर समान कोण अन्तरित करती है।
\angle 2=\angle 3 \\ \angle 4=\angle 5, \angle 6=\angle 7 \text { तथा } \angle 8=\angle 1
वृत्त के केन्द्र-बिन्दु O पर बने सभी कोणों का योग 360° होता है।
=\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8=360^{\circ} \\ \Rightarrow \angle 1+\angle 2+\angle 2+\angle 5+\angle 5+\angle 6+\angle 6+\angle 1=360^{\circ} \\ \Rightarrow \quad 2(\angle 1+\angle 2+\angle 5+\angle 6)=360^{\circ} \\ \Rightarrow(\angle 1+\angle 2)+(\angle 5+\angle 6)=180^{\circ} \\ \Rightarrow \angle P O Q+\angle S O R=180^{\circ} [ \because \angle 1+\angle 2=\angle P O Q \text { तथा } \angle 5+\angle 6=\angle SOR ]
इसी प्रकार \angle SOR+\angle ROQ=180^{\circ}
अतः वृत्त के परिगत बने चतुर्भुज के आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती है।
उपर्युक्त उदाहरणों के द्वारा वृत्त की स्पर्श रेखा कक्षा 10 (Tangent to Circle Class 10),एक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या (Number of Tangents from a Point on a Circle) को समझ सकते हैं।
3.वृत्त की स्पर्श रेखा कक्षा 10 पर आधारित सवाल (Questions Based on Tangent to Circle Class 10):
(1.)सिद्ध करो कि वृत्त की किसी जीवा के सिरों पर खींची गई स्पर्श रेखाएँ,जीवा से समान कोण बनाती है।
(2.)चित्र में वृत्त का केन्द्र O है और बाह्य बिन्दु P से खींची गई स्पर्श रेखाएँ PA एवं PB वृत्त को क्रमशः A और B पर स्पर्श करती है।सिद्ध कीजिए कि OP रेखाखण्ड AB का लम्ब समद्विभाजक है।
उपर्युक्त सवालों को हल करने पर वृत्त की स्पर्श रेखा कक्षा 10 (Tangent to Circle Class 10),एक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या (Number of Tangents from a Point on a Circle) को ठीक से समझ सकते हैं।
Also Read This Article:-Applications of Trigonometry Class 10
4.वृत्त की स्पर्श रेखा कक्षा 10 (Frequently Asked Questions Related to Tangent to Circle Class 10),एक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या (Number of Tangents from a Point on a Circle) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.बाह्य बिन्दु से किसी वृत्त पर खींचे गए रेखाखण्डों के बीच कोण तथा केन्द्र पर बनाए कोण में क्या सम्बन्ध होता है? (What is Relation Between the Angle of Two Tangents and Angle at the Centre?):
उत्तर:एक बाह्य बिन्दु से किसी वृत्त पर खींची गई दो स्पर्श रेखाएँ,बाह्य बिन्दु को वृत्त के केन्द्र से मिलाने वाली रेखा के साथ तुल्य कोण बनाता है।
प्रश्न:2.एक बिन्दु से वृत्त पर कितनी स्पर्श रेखाएँ खींची जा सकती हैं? (How Many Tangents Lines Can be Drawn from One Point to a Circle?):
उत्तर:एक बिन्दु से एक वृत्त पर कितनी स्पर्श रेखाएँ खींची जा सकती हैं यह वृत्त के सापेक्ष बिन्दु की स्थिति पर निर्भर करता है।
(1.)यदि बिन्दु वृत्त पर स्थित है तो इस बिन्दु से वृत्त की केवल एक स्पर्श रेखा खींची जा सकती है।
(2.)यदि बिन्दु वृत्त के अन्दर स्थित हो तो इससे होकर जानेवाली कोई भी रेखा वृत्त को दो बिन्दुओं पर प्रतिच्छेद करती है।अतः यह रेखा स्पर्श रेखा नहीं हो सकती है अर्थात् वृत्त के अन्दर स्थित बिन्दु से वृत्त पर कोई भी स्पर्श रेखा नहीं खींची जा सकती है।
(3.)यदि बिन्दु वृत्त के बाहर स्थित हो तो वृत्त के बाहर बिन्दु से वृत्त पर अधिकतम दो स्पर्श रेखाएँ खींची जा सकती हैं।
प्रश्न:3.स्पर्श रेखा के मुख्य बिन्दु लिखिए। (Write HIGHLIGHTS of the Tangents):
उत्तर:(1.) वृत्त की दो स्पर्श रेखाओं की लम्बाई समान होती है।
(2.)स्पर्श रेखा और वृत्त के उभयनिष्ठ बिन्दु को स्पर्श बिन्दु कहते हैं।
(3.)वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु से जाने वाली त्रिज्या के समान्तर नहीं होती है।
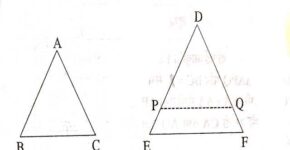
(4.)समद्विबाहु त्रिभुज ABC के परिगत वृत्त पर बिन्दु A से स्पर्श रेखाएँ इस प्रकार है कि AB=AC और BC के समान्तर है।
उपर्युक्त प्रश्नों के उत्तर द्वारा वृत्त की स्पर्श रेखा कक्षा 10 (Tangent to Circle Class 10),एक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या (Number of Tangents from a Point on a Circle) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Tangent to Circle Class 10
वृत्त की स्पर्श रेखा कक्षा 10
(Tangent to Circle Class 10)
Tangent to Circle Class 10
वृत्त की स्पर्श रेखा कक्षा 10 (Tangent to Circle Class 10) के इस आर्टिकल में एक बिन्दु
से एक वृत्त पर स्पर्श रेखाओं की संख्या तथा स्पर्श रेखा की लम्बाई का अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.