Applications of Trigonometry Class 10
1.त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Applications of Trigonometry Class 10),त्रिकोणमिति के कुछ अनुप्रयोग कक्षा 10 (Some Applications of Trigonometry Class 10):
त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Applications of Trigonometry Class 10) के इस आर्टिकल में वास्तविक माप के बिना प्रयोग के हमारे आस-पास के जीवन से जुड़ी हुई वस्तुओं की ऊँचाईयाँ और दूरियाँ ज्ञात करने के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Trigonometrical Identities Class 10
2.त्रिकोणमिति के अनुप्रयोग कक्षा 10 के उदाहरण (Applications of Trigonometry Class 10 Examples):
Example:1.सर्कस का एक कलाकार एक 20 मीटर लम्बी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खम्भे के शिखर से बंधा हुआ है।यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो तो खम्भे की ऊँचाई ज्ञात कीजिए।(देखिए आकृति)।
Solution:माना खम्भे की ऊँचाई AB=h मीटर
तथा डोरी AC की लम्बाई=20 मीटर
समकोण \triangle ABC में
\sin \theta=\frac{\text { लम्ब }}{\text { कर्ण }}=\frac{AB}{AC} \\ \Rightarrow \sin 30^{\circ}=\frac{h}{20} \\ \Rightarrow \frac{1}{2}=\frac{h}{20} \\ \Rightarrow h=\frac{20}{2} \\ \Rightarrow h=10 \text { मीटर }
Example:2.आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है।पेड़ के पाद बिन्दु की दूरी,जहाँ पेड़ का शिखर जमीन को छूता है,8m है।पेड़ की ऊँचाई ज्ञात कीजिए।
Solution:माना टूटने से पहले पेड़ की लम्बाई=BD
आँधी से पेड़ A स्थान से टूटकर पेड़ का शीर्ष जमीन को C बिन्दु पर स्पर्श करता है।
अर्थात् AD=AC=h_{2}(माना)
और AB=h_{1} मीटर (माना)
समकोण \triangle ABC में
\tan \theta=\frac{\text { लम्ब }}{\text { आधार }}=\frac{A B}{B C} \\ \Rightarrow \tan 30^{\circ} =\frac{h_{1}}{8} \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{h_{1}}{8} \\ \Rightarrow h_{1}=\frac{8}{\sqrt{3}}
पुनः समकोण \triangle ABC में
\cos 30^{\circ}=\frac{B C}{A C} \\ \Rightarrow \frac{\sqrt{3}}{2}=\frac{8}{h_{2}} \\ \Rightarrow h_2=\frac{16}{\sqrt{3}}
पेड़ की ऊँचाई (BD)=AB+AD
=h_1+h_2 \\ =\frac{8}{\sqrt{3}}+\frac{16}{\sqrt{3}}=\frac{24}{\sqrt{3}} \\ =\frac{8 \times 3}{\sqrt{3}}=\frac{8 \sqrt{3} \times \sqrt{3}}{\sqrt{3}} \\ \text{ BD }=8 \sqrt{3} मीटर
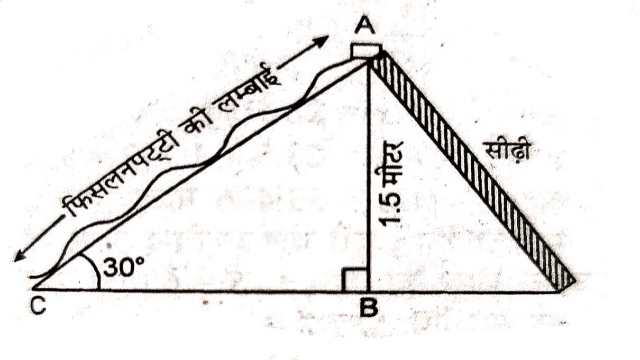
Example:3.एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलन पट्टी लगाना चाहती है।5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलन पट्टी लगाना चाहती है जिसका शिखर 1.5 मीटर की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो जबकि इससे अधिक उम्र के बच्चों के लिए वह 3m की ऊँचाई पर एक अधिक ढाल की फिसलन पट्टी लगाना चाहती है,जो भूमि के साथ 60° का कोण बनाती हो।प्रत्येक स्थिति में फिसलन पट्टी की लम्बाई क्या होनी चाहिए?
Solution:5 वर्ष से कम उम्र के बच्चों के लिए फिसलन पट्टी की ऊँचाई AB=1.5 मीटर
तथा \angle ACB=30°
माना फिसलन पट्टी की लम्बाई AC=x
समकोण \triangle ABC में
\sin \theta=\frac{\text { लम्ब }}{\text { कर्ण }} \\ \sin 30=\frac{AB}{AC} \\ \Rightarrow \frac{1}{2}=\frac{1.5}{x} \\ \Rightarrow x=3 \text { मीटर }
5 वर्ष से अधिक उम्र के बच्चों के लिए फिसलन पट्टी की ऊँचाई PQ=3 मीटर
माना फिसलन पट्टी की लम्बाई PR=h
समकोण \triangle PQR में
\sin \theta=\frac{\text { लम्ब }}{\text { कर्ण }} \\ \Rightarrow \sin 60^{\circ}=\frac{P Q}{P R} \\ \Rightarrow \frac{\sqrt{3}}{2}=\frac{3}{h} \\ \Rightarrow h=\frac{6}{\sqrt{3}} \\ \Rightarrow h=2 \sqrt{3} \text { मीटर }
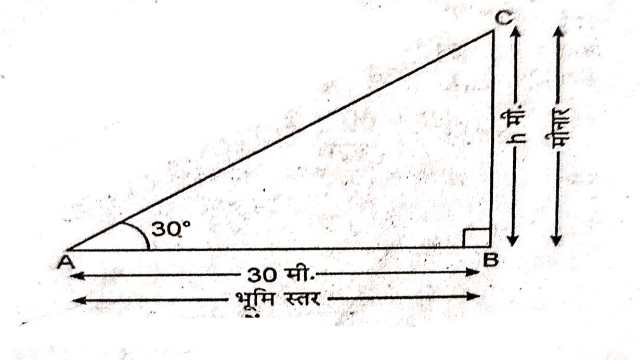
Example:4.भूमि के एक बिन्दु से, जो मीनार के पाद बिन्दु से 30m की दूरी पर है,मीनार के शिखर का उन्नयन कोण 30° है।मीनार की ऊँचाई ज्ञात कीजिए।
Solution:माना मीनार की ऊँचाई BC=h मीटर
AB=30 मीटर, \angle BAC= 30^{\circ}
समकोण \triangle ABC में
\tan 30^{\circ} =\frac{\text { लम्ब }}{\text { आधार }} \\ \tan 30^{\circ} =\frac{B C}{A B} \\ \Rightarrow \frac{1}{\sqrt{3}} =\frac{h}{30} \\ \Rightarrow h =\frac{30}{\sqrt{3}} \\ \Rightarrow h=10 \sqrt{3} \text { मीटर }
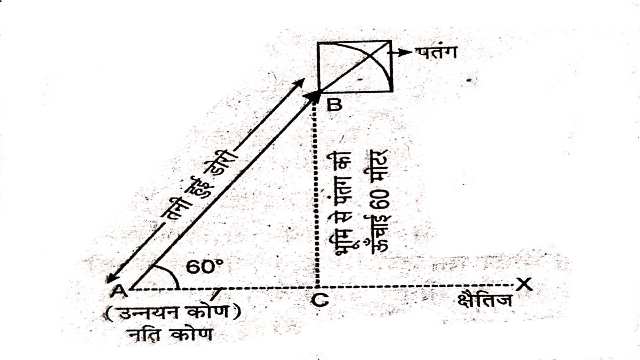
Example:5.भूमि से 60m की ऊँचाई पर एक पतंग उड़ रही है।पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिन्दु से बांध दिया गया है।भूमि के साथ डोरी का झुकाव 60° है।यह मानकर कि डोरी में कोई ढील नहीं है,डोरी की लम्बाई ज्ञात कीजिए।
Solution:माना पतंग से लगी डोरी की लम्बाई=AB
पतंग की भूमि से ऊँचाई BC=60 मीटर
\angle CAB=60^{\circ}
समकोण \triangle ACB में
\sin \theta=\frac{\text { लम्ब }}{\text { कर्ण }} \\ \Rightarrow \sin 60^{\circ}=\frac{B C}{A B} \\ \Rightarrow \frac{\sqrt{3}}{2}=\frac{60}{ AB } \\ \Rightarrow AB=\frac{120}{\sqrt{3}} \\ \Rightarrow AB=40 \sqrt{3} \text { मीटर }
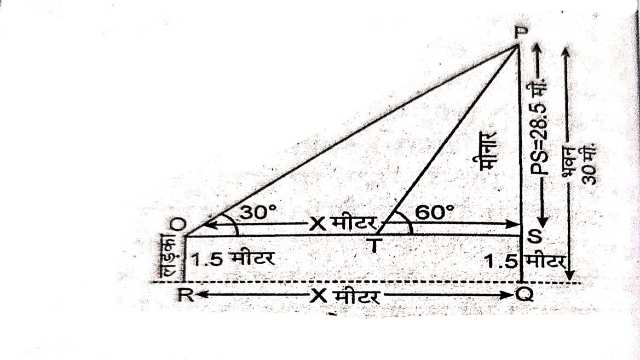
Example:6.1.5m लम्बा एक लड़का 30m ऊँचे एक भवन से कुछ दूरी पर खड़ा है।जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है।बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है।
Solution:भवन की ऊँचाई PQ=30 मीटर
लड़के की ऊँचाई OR=1.5 मीटर
माना लड़के की भवन के आधार S से दूरी QR=OS=x मीटर
OS \parallel RQ तथा OR \parallel SQ
SQ=OR=1.5 मीटर, PS=PQ-QS=30-1.5= 28.5 मीटर
समकोण \triangle PSO में
\tan \theta=\frac{\text { लम्ब }}{\text { आधार }} \\ \tan 30^{\circ}=\frac{ PS }{ OS } \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{28.5}{x} \\ \Rightarrow x=28.5 \sqrt{3}
समकोण \triangle PTS में
\tan 60^{\circ}=\frac{P S}{S T} \\ \sqrt{3}=\frac{28.5}{TS} \\ \Rightarrow TS=\frac{28.5}{\sqrt{3}}
लड़के द्वारा भवन की ओर तय की गई दूरी (OT)=OS-TS
= OS-T S=28.5 \sqrt{3}-\frac{28.5}{\sqrt{3}} \\ = 28.5\left(\sqrt{3}-\frac{1}{\sqrt{3}}\right) \\ =28.5\left( \frac{3-1}{\sqrt{3}}\right) \\=\frac{28.5 \times 2}{\sqrt{3}}=\frac{57}{\sqrt{3}} \\ \Rightarrow OT =19 \sqrt{3} \text { मीटर }
Example:7.भूमि के एक बिन्दु से एक 20m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° है।मीनार की ऊँचाई ज्ञात कीजिए।
Solution:भवन की ऊँचाई BC=20 मीटर
संचार मीनार की ऊँचाई=CD
\angle BAC=45^{\circ}, \angle BAD=60^{\circ}
समकोण \triangle ABC में
\tan \theta=\frac{\text { लम्ब }}{\text { आधार }} \\ \Rightarrow \tan 45^{\circ}=\frac{B C}{A R^{\circ}} \\ \Rightarrow 1=\frac{B C}{A B } \Rightarrow AB=BC \\ \Rightarrow AB=20 \text { मीटर }
समकोण \triangle ABD में
\Rightarrow \tan 60^{\circ}=\frac{B D}{A B} \\ \Rightarrow \sqrt{3}=\frac{B D}{20} \\ \Rightarrow B D=20 \sqrt{3} \text { मीटर }
संचार मीनार की ऊँचाई CD=BD-BC=20 \sqrt{3}-20 \\ \Rightarrow CD =20(\sqrt{3}-1)
Example:8.एक पेडस्टल के शिखर पर एक 1.6m ऊँची मूर्ति लगी है।भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है।पेडस्टल की ऊँचाई ज्ञात कीजिए।
Solution:माना पेडस्टल की ऊँचाई BC=h मीटर
तथा मूर्ति की ऊँचाई CD=1.6 मीटर
\angle BAC=45^{\circ}, \angle BAD=60^{\circ}
समकोण \triangle ABC में
\tan \theta=\frac{\text { लम्ब }}{\text { अधार }} \\ \Rightarrow \tan 45^{\circ}=\frac{B C}{A B} \\ \Rightarrow 1=\frac{B C}{A B}
AB=BC=h मीटर
समकोण \triangle ABD में
\tan 60^{\circ}=\frac{B D}{A B} \\ \Rightarrow \sqrt{3}=\frac{B C+C D}{h} \\ \Rightarrow \sqrt{3} h=h+1.6 \\ \Rightarrow \sqrt{3} h-h=1.6 \\ \Rightarrow h(\sqrt{3}-1)=1.6 \\ \Rightarrow h=\frac{1.6}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1} \\ \Rightarrow h=\frac{1.6(\sqrt{2}+1)}{3-1} \\ \Rightarrow h=0.8(\sqrt{3}-1) \text { मीटर }
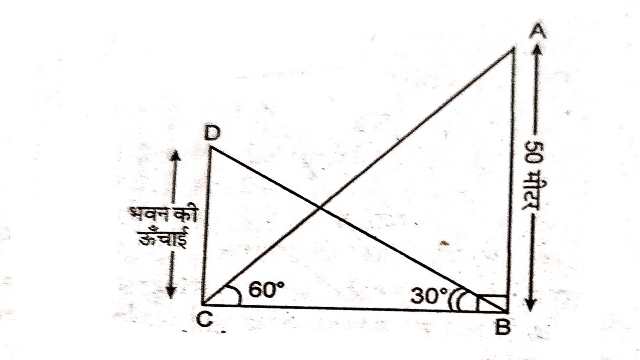
Example:9.एक मीनार के पाद-बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है।यदि मीनार 50m ऊँची हो तो भवन की ऊँचाई ज्ञात कीजिए।
Solution:मीनार की ऊँचाई AB=50 मीटर
माना भवन की ऊँचाई CD=h मीटर
\angle BCA=60^{\circ}, \angle CBD=30^{\circ}
समकोण \triangle ABC में
\tan \theta=\frac{\text { लम्ब }}{\text{आधार}} \\ \tan 60^{\circ}=\frac{A B}{B C} \\ \Rightarrow \sqrt{3}=\frac{50}{B C} \\ \Rightarrow B C=\frac{50}{\sqrt{3}}
पुनः समकोण \triangle BCD में
\tan 30^{\circ}=\frac{C D}{B C} \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{C D}{\frac{50}{\sqrt{3}}} \\ \Rightarrow C D=\frac{50}{\sqrt{3} \times \sqrt{3}}=\frac{50}{3} \\ \Rightarrow CD=16 \frac{2}{3} \text { मीटर }
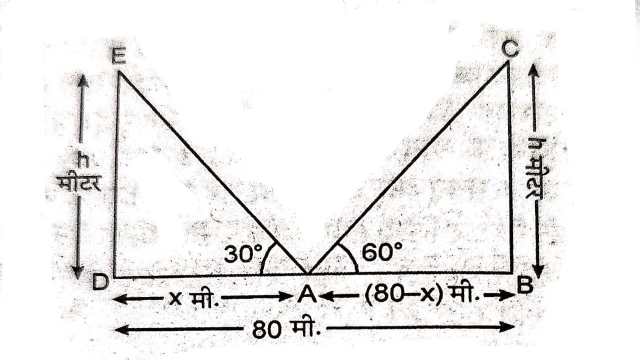
Example:10.एक 80m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खम्भे लगे हुए हैं।इन दोनों खम्भों के बीच सड़क के एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमशः 60° और 30° है।खम्भों की ऊँचाई और खम्भों से बिन्दु की दूरी ज्ञात कीजिए।
Solution:माना खम्भों की ऊँचाई BC=DE=h मीटर
दोनों के बीच बिन्दु A,की B से दूरी=AB
\angle DAE=30^{\circ},\angle BAC=60^{\circ}
माना DA=x,
AB=BD-DA
AB=80-x
समकोण \triangle ADE में
\tan \theta=\frac{\text { लम्ब }}{\text { आघार }} \\ \Rightarrow \tan 30^{\circ}=\frac{D E}{D A} \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x} \\ \Rightarrow h=\sqrt{x} \ldots(1)
पुनः समकोण \triangle ABC में
\tan 60^{\circ} =\frac{B C}{A B} \\ \Rightarrow \sqrt{3} =\frac{h}{30-21} \\ \Rightarrow h =\sqrt{3}(80-x) \ldots(2)
समीकरण (1) व (2) सेः
\frac{x}{\sqrt{3}}=\sqrt{3}(80-x) \\ \Rightarrow x=3(80-x) \\ \Rightarrow x=240-3 x \\ \Rightarrow x+3 x=240 \\ \Rightarrow 4 x=240 \\ \Rightarrow x=\frac{240}{4} \\ \Rightarrow x=60 मीटर
AB=80-x=80-60=20 मीटर
समीकरण (1) में मान रखने परः
h=\frac{60}{\sqrt{3}} \Rightarrow h=20 \sqrt{3} \text { मीटर }
खम्भों की ऊँचाई=20 \sqrt{3} मीटर,बिन्दु की खम्भों से दूरी=20,60 मीटर
Example:11.एक नहर के एक तट पर एक टीवी टाॅवर उर्ध्वाधर खड़ा है।टाॅवर के ठीक सामने दूसरे तट के अन्य बिन्दु से टाॅवर के शिखर का उन्नयन कोण 60° है।इसी तट पर इस बिन्दु से 20m दूर और इस बिन्दु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टाॅवर के शिखर का उन्नयन कोण 30° है।(देखिए आकृति)।टाॅवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।
Solution:माना टाॅवर की ऊँचाई AB=h मीटर
माना नहर की चौड़ाई BC=x मीटर
\angle BCA=60^{\circ}, \angle BDA=30^{\circ}
समकोण \triangle ABC में
\tan 60^{\circ}=\frac{\text { लम्ब }}{\text { आधार }} \\ \sqrt{3}=\frac{A B}{B C} \\ \Rightarrow \sqrt{3}=\frac{h}{x} \\ \Rightarrow h=\sqrt{3} x \ldots(1)
पुनः समकोण \triangle BDA में
\tan 30^{\circ}=\frac{A B}{B D} \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x+20} \\ \Rightarrow h=\frac{x+20}{\sqrt{3}} \ldots(2)
समीकरण (1) व (2) सेः
\sqrt{3} x=\frac{x+20}{\sqrt{3}} \\ \Rightarrow 3 x=x+20 \\ \Rightarrow 2 x=20 \Rightarrow x=10 \text { मीटर }
BC=10 मीटर
x का मान समीकरण (1) में रखने परः
h=\sqrt{3} \times 10 \\ \Rightarrow h=10 \sqrt{3} मीटर
मीनार की ऊँचाई=10 \sqrt{3} मीटर, नहर की चौड़ाई=10 मीटर
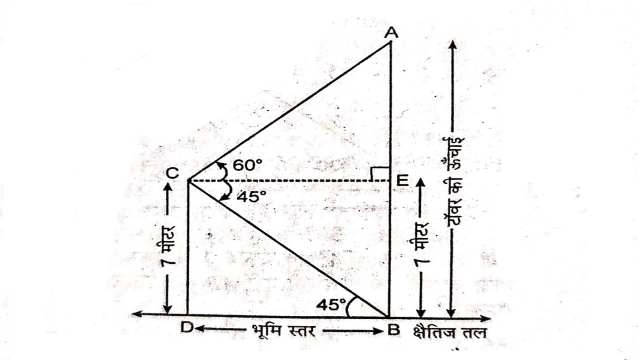
Example:12.7m ऊँचे भवन के शिखर से एक केबल टाॅवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है।टाॅवर की ऊँचाई ज्ञात कीजिए।
Solution:माना केबल टाॅवर की ऊँचाई=AB
\angle ACE=60^{\circ},\angle BCE=45^{\circ} \\ BD \parallel CE \\ \angle DBC=\angle BCE=45^{\circ}(एकान्तर कोण)
समकोण \triangle BDC में
\tan \theta=\frac{\text { लम्ब }}{\text{आधार}} \\ \tan 45^{\circ}=\frac{C D}{D B} \\ \Rightarrow 1=\frac{7}{DB} \Rightarrow BD=7 \text { मीटर }
BD=CE=7 मीटर
पुनः समकोण \triangle AEC में
\tan 60^{\circ} =\frac{A E}{C E} \\ \Rightarrow \sqrt{3} =\frac{A E}{7} \\ \Rightarrow A E=7 \sqrt{3}
टाॅवर की ऊँचाई AB=AE+BE =7 \sqrt{3}+7 \\ \Rightarrow AB=7(\sqrt{3}+1)
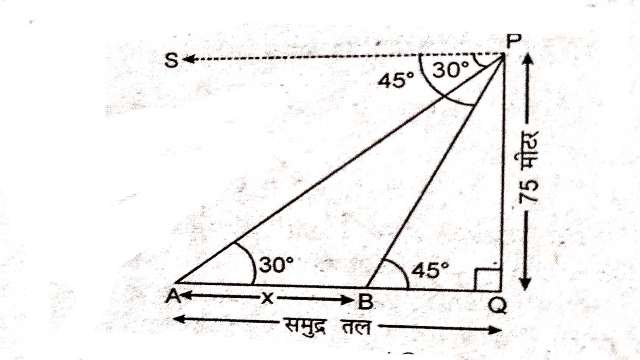
Example:13.समुद्र-तल से 75m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं।यदि लाइट हाउस के एक ही ओर जहाज एक दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच दूरी ज्ञात कीजिए।
Solution:प्रकाश स्तम्भ की ऊँचाई PQ=75 मीटर
P S \| A Q
अतः \angle SPA=\angle PAQ=30^{\circ} (एकान्तर कोण)
\angle SPB=\angle PBQ=45^{\circ} (एकान्तर कोण)
माना जहाजों के बीच दूरी AB=x मीटर
समकोण \triangle PQB में
\tan \theta=\frac{\text { लम्ब }}{\text { आधार }} \\ \Rightarrow \tan 45^{\circ}=\frac{P Q}{Q B} \\ \Rightarrow 1=\frac{75}{Q B} \\ \Rightarrow Q B=75 मीटर
पुनः समकोण \triangle PQA में
\tan 30^{\circ}=\frac{P Q}{Q A} \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{75}{A B+Q B} \\ \Rightarrow A B+Q B=75 \sqrt{3} \\ \Rightarrow A B+75=75 \sqrt{3} \\ \Rightarrow A B=75 \sqrt{3}-75 \\ \Rightarrow A B=75(\sqrt{3}-1)
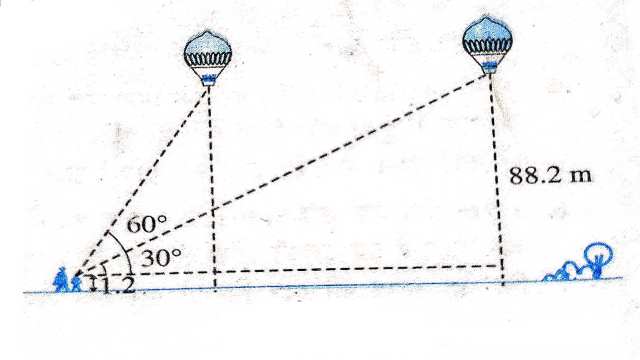
Example:14.1.2m लम्बी एक लड़की भूमि से 88.2m की ऊँचाई पर क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है।किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है।कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है (देखिए आकृति)।इस अन्तराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।
Solution:लड़की की ऊँचाई=1.2 मीटर
BC=CD=88.2 मीटर
\angle CAD=30^{\circ}, \angle CAE=60^{\circ}
समकोण \triangle ACD में
\tan \theta=\frac{\text { लम्ब }}{\text { आधार }} \\ \Rightarrow \tan 30^{\circ}=\frac{C D}{A C} \\ \Rightarrow \frac{1}{\sqrt{3}}=\frac{88.2}{AC} \\ \Rightarrow A C=88.2 \sqrt{3} \text { मीटर }
पुनः समकोण \triangle ABE में
\tan 60^{\circ}=\frac{B E}{A B} \\ \Rightarrow \sqrt{3}=\frac{88.2}{A B} \\ \Rightarrow A B= \frac{88.2}{\sqrt{3}} \\ \Rightarrow B C=A C-A B \\ =88.2 \times \sqrt{3}-\frac{88.2}{\sqrt{3}} \\ =88.2 \left(\sqrt{3}-\frac{1}{\sqrt{3}}\right) \\ =88.2\left(\frac{3-1}{\sqrt{3}}\right) \\ =88.2\left(\frac{2}{\sqrt{3}}\right) \\ =\frac{176.4}{\sqrt{3}} \\ =58.8 \sqrt{3}
गुब्बारे द्वारा तय की गई दूरी=58.8 \sqrt{3} मीटर
Example:15.एक सीधा राजमार्ग एक मीनार के पाद तक जाता है।मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एक समान चाल से जाता है।छः सेकण्ड बाद कार का अवनमन कोण 60° हो गया।इस बिन्दु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
Solution:माना मीनार की ऊँचाई AD=h मीटर
6 सेकण्ड में कार द्वारा तय की गई दूरी=BC
\angle DCA=60^{\circ}, \angle DBA=30^{\circ}
समकोण \triangle ABD में
\tan \theta=\frac{\text { लम्ब }}{\text { आधार }} \\ \tan 30^{\circ}=\frac{A D}{B D} \\ \frac{1}{\sqrt{3}}=\frac{h}{B D} \\ \Rightarrow h=\frac{B D}{\sqrt{3}} \ldots(1)
पुनः समकोण \triangle ADC में
\tan 60 =\frac{A D}{C D} \\ \Rightarrow \sqrt{3} =\frac{h}{C D} \Rightarrow h=\sqrt{3} \text{CD} \ldots(2)
समीकरण (1) व (2) सेः
\sqrt{3} CD=\frac{B D}{\sqrt{3}} \\ \Rightarrow C D=\frac{1}{3} BD \\ C D=\frac{1}{3} \left(BC+ CD\right) \\ \Rightarrow CD-\frac{1}{3} C D=\frac{1}{3} B C \\ \Rightarrow \frac{2}{3} C D=\frac{1}{3} B C \\ \Rightarrow C D=\frac{1}{2} B C
CD दूरी चलने में लगा समय=\frac{1}{2} \times 6=3 सेकण्ड
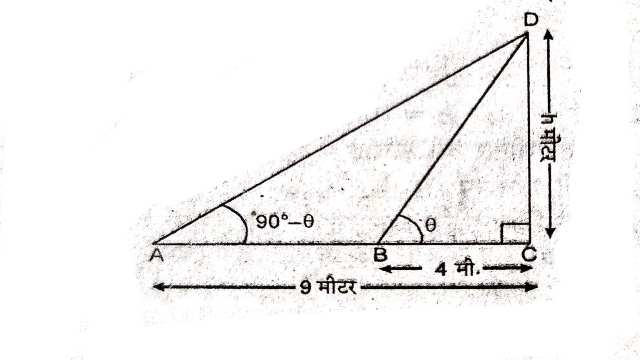
Example:16.मीनार के आधार से और एक सरल रेखा में 4m और 9m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं।सिद्ध कीजिए कि मीनार की ऊँचाई 6 मीटर है।
Solution:BC=4 मीटर तथा AC=9 मीटर
माना \angle ABC=\theta \\ \angle CAD=90-\theta
समकोण \triangle PCB में
\tan \theta=\frac{\text { लम्ब }}{\text{ आधार } } \\ \tan \theta=\frac{h}{B C} \Rightarrow \tan \theta=\frac{h}{4} \\ \Rightarrow h=4 \tan \theta \ldots(1)
पुनः समकोण \triangle ACD में
\tan (90-\theta)=\frac{C D}{A C} \\ \cot \theta=\frac{h}{9} \Rightarrow h=9 \cot \theta \ldots(2)
(1) व (2) को गुणा करने परः
\Rightarrow h \times h=4 \tan \theta \times 9 \cot \theta \\ \Rightarrow h^2=36 \Rightarrow h=\sqrt{36}=6 \text { मीटर }
उपर्युक्त उदाहरणों द्वारा त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Applications of Trigonometry Class 10),त्रिकोणमिति के कुछ अनुप्रयोग कक्षा 10 (Some Applications of Trigonometry Class 10) को समझ सकते हैं।
3.त्रिकोणमिति के अनुप्रयोग कक्षा 10 की समस्याएँ (Applications of Trigonometry Class 10 Problems):
(1.)किसी स्तम्भ की चोटी का उन्नतांश समतल पर स्थित एक बिन्दु से 15° है।स्तम्भ की ओर 100 मीटर चलने पर उन्नतांश 30° हो जाता है।स्तम्भ की ऊँचाई ज्ञात कीजिए।
(2.)100 मीटर चौड़ी एक नदी के मध्य में एक छोटा टापू है।इस टापू पर एक ऊँचा वृक्ष है।नदी के विपरीत किनारों पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि P,Q और वृक्ष एक रेखा में हैं।यदि P और Q से वृक्ष की चोटी के उन्नयन कोण 30° और 45° हो तो वृक्ष की ऊँचाई ज्ञात कीजिए।
उत्तर (Answers):(1.)स्तम्भ की ऊँचाई=50 मीटर
(2.)वृक्ष की ऊँचाई=36.6 मीटर
उपर्युक्त सवालों को हल करने पर त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Applications of Trigonometry Class 10),त्रिकोणमिति के कुछ अनुप्रयोग कक्षा 10 (Some Applications of Trigonometry Class 10) को ठीक से समझ सकते हैं।
Also Read This Article:-Complementary Angles Class 10
4.त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Frequently Asked Questions Related to Applications of Trigonometry Class 10),त्रिकोणमिति के कुछ अनुप्रयोग कक्षा 10 (Some Applications of Trigonometry Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.उन्नयन कोण किसे कहते हैं? (What is the Angle of Elevation?):
उत्तरःजब कोई वस्तु,आँख से ऊपर हो तो दृष्टि रेखा, क्षैतिज के साथ जो कोण बनाती है उसे उन्नयन कोण या उन्नतांश या उन्नति कोण कहते हैं।
प्रश्न:2.अवनमन कोण किसे कहते हैं? (What is the Angle of Depression?):
उत्तरःजब कोई वस्तु,आँख से नीचे हो तो दृष्टि रेखा, क्षैतिज के साथ जो कोण बनाती है उसे अवनमन कोण या अवनति कोण कहते हैं।
प्रश्न:3.दृष्टि रेखा किसे कहते हैं? (What is a Line of Sight?):
उत्तरःजब हम किसी वस्तु (object) को देखते हैं, तो हमारी आँख और वस्तु को जोड़ने वाली रेखा को दृष्टि रेखा कहते हैं।
प्रश्नः4.त्रिकोणमिति में ऊँचाई एवं दूरी की समस्याओं को हल करते समय किन बातों का ध्यान रखना चाहिए? (What Should be Kept in Mind While Solving Height and Distance in Trigonometry?):
उत्तरःऊँचाई एवं दूरी की समस्याओं को हल करते समय निम्नलिखित बिन्दुओं को ध्यान में रखना चाहिएः
(1.)सर्वप्रथम प्रश्न को ध्यानपूर्वक पढ़ने के उपरान्त चित्र बनाकर समकोण त्रिभुज का निर्माण करते हैं।
(2.)समकोण त्रिभुज में ज्ञात कोण का त्रिकोणमितीय अनुपातों (sine,cosine,tangent)आदि को ज्ञात भुजा के पदों में व्यक्त करते हैं।
(3.)दो वस्तुओं के बीच एक से दूसरे का उन्नयन कोण एवं दूसरी से पहली का अवनमन कोण समान होते हैं।
एक वस्तु का दूसरी के सापेक्ष उन्नयन कोण= दूसरी का पहली के सापेक्ष अवनमन कोण
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Applications of Trigonometry Class 10),त्रिकोणमिति के कुछ अनुप्रयोग कक्षा 10 (Some Applications of Trigonometry Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Applications of Trigonometry Class 10
त्रिकोणमिति के अनुप्रयोग कक्षा 10
(Applications of Trigonometry Class 10)
Applications of Trigonometry Class 10
त्रिकोणमिति के अनुप्रयोग कक्षा 10 (Applications of Trigonometry Class 10) के इस आर्टिकल
में वास्तविक माप के बिना प्रयोग के हमारे आस-पास के जीवन से जुड़ी हुई वस्तुओं की ऊँचाईयाँ
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.