Basic Proportionality Theorem
1.आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem)-
आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem) को थेल्स प्रमेय (Thales Theorem) भी कहते हैं।क्योंकि थेल्स (लगभग 600 ई.पू.) जिन्होंने यूनान में ज्यामिति के अध्ययन की शुरुआत की,ने समरूप त्रिभुजों से सम्बद्ध एक महत्त्वपूर्ण तथ्य,”समरूप त्रिभुजों में सदैव किन्हीं दो संगत भुजाओं की लम्बाइयों का अनुपात समान होता है” को सिद्ध किया था।
इस आर्टिकल में आधारभूत आनुपातिकता प्रमेय के साथ-साथ,आनुपातिकता प्रमेय कथन,आधारभूत आनुपातिकता प्रमेय प्रमाण के बारे में अध्ययन करेंगे।
प्रमेय (Theorem):1.आधारभूत आनुपातिकता प्रमेय कथन (State basic Proportionality Theorem),आधारभूत आनुपातिकता प्रमेय प्रमाण (Basic Proportionality Theorem Proof),थेल्स प्रमेय प्रमाण (Thales Theorem Prove),थेल्स प्रमेय कथन (Thales Theorem State)-
किसी त्रिभुज की एक भुजा के समांतर खींची गई रेखा अन्य दो भुजाओं को जिन बिंदुओं पर प्रतिच्छेद करती है वे बिंदु उन भुजाओं को समान अनुपात में विभाजित करते हैं।
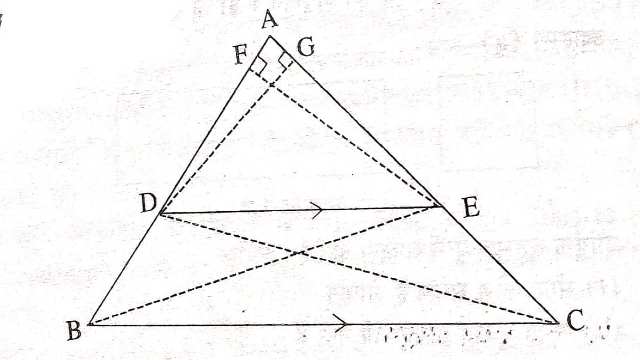
दिया है (Given): \triangle ABC में DE \parallel BC खींची गई है और यह AB को D पर तथा AC को E पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove):\frac{A D}{D B}=\frac{A E}{E C}
रचना (Construction):B को E से तथा C को D से मिलाइए और E F \perp B A तथा D G \perp A C खींचिए।
उपपत्ति (Proof): \triangle BDE तथा \triangle CDE एक ही आधार DE पर तथा समान्तर रेखा DE तथा BC के बीच स्थित है।
\therefore \triangle BDE का क्षेत्रफल=\triangle CDE का क्षेत्रफल …..(1)
\triangle ADE तथा \triangle BDE की उभयनिष्ठ ऊंचाई EF है
\therefore \frac{\text{ क्षेत्रफल }(\triangle A D E)}{ \text{ क्षेत्रफल }(\triangle B D E)}=\frac{\frac{1}{2} \times A D \times E F}{\frac{1}{2} \times DB \times EF} \\ \Rightarrow \frac{ar(\triangle A D E)}{ar(\triangle B D E)}=\frac{A D}{D B} \quad \cdots (2)
\triangle A D E तथा \triangle B D E की उभयनिष्ठ ऊंचाई DG है
\therefore \frac{\text{ क्षेत्रफल }(\triangle A D E)}{ \text{ क्षेत्रफल }(\triangle C D E)}=\frac{\frac{1}{2} \times A E \times DG}{\frac{1}{2} \times EC \times DG} \\ \Rightarrow \frac{ar(\triangle A D E)}{ar(\triangle C D E)}=\frac{A E}{EC} \quad \cdots (3)
समीकरण (1),(2) तथा (3) से-
\frac{A D}{D B}=\frac{A E}{E C}
उपप्रमेय (Corollary):यदि \triangle ABC में एक रेखा DE इस प्रकार है कि D E \| B C तथा यह भुजा AB को D पर तथा भुजा AC को E पर काटती है तो
(1) \frac{A B}{A D}=\frac{A C}{A E} तथा (2) \frac{A B}{D B}=\frac{A C}{E C}
उपपत्ति (Proof): \triangle ABC में D E \| B C है अतः आधारभूत आनुपातिकता प्रमेय से
\frac{A D}{D B}=\frac{A E}{E C} \\ \Rightarrow \frac{D B}{A D}=\frac{E C}{A E} (विलोमानुपात से)
\Rightarrow \frac{D B}{A D}+1=\frac{E C}{A E}+1 \\ \Rightarrow \frac{D B+A D}{A D}=\frac{E C+A E}{A E} (योगानुपात से)
\Rightarrow \frac{A B}{A D}=\frac{A C}{A E}
(2) \triangle ABC में D E \| B C है अतः आधारभूत आनुपातिकता प्रमेय से
\frac{A D}{D B}=\frac{A E}{E C} \\ \Rightarrow \frac{A D}{D B} +1=\frac{A E}{E C}+1 \\ \Rightarrow \frac{A D+D B}{D B}=\frac{A E+E C}{E C} (योगानुपात से)
\Rightarrow \frac{A B}{D B}=\frac{A C}{E C}
उपर्युक्त परिणामों के अनुसार हमें आधारभूत आनुपातिकता प्रमेय के निम्न उपप्रमेय प्राप्त होते हैं –
यदि \triangle ABC में D E \| B C और यह AB को D पर तथा AC को E पर प्रतिच्छेद करती है तो-
(1) \frac{D B}{A D}=\frac{E C}{A E} \\ (2) \frac{A B}{D B}=\frac{A C}{E C} \\ (3) \frac{A B}{A D}=\frac{A C}{A E} \\ (4) \frac{D B}{A B}=\frac{E C}{A C} \\ (5) \frac{A D}{A B}=\frac{A E}{A C}
प्रमेय (Theorem)-2.आधारभूत आनुपातिकता प्रमेय का विलोम (Converse of Basic Proportionality Theorem)-
यदि कोई रेखा एक त्रिभुज की दो भुजाओं को समान अनुपात में विभाजित करती हो तो यह रेखा तीसरी भुजा के समांतर होती है।
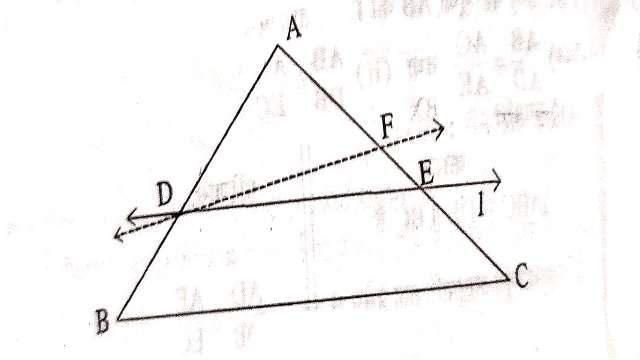
दिया है (Given): \triangle ABC में रेखा l भुजा AB को D पर और AC को E पर इस प्रकार प्रतिच्छेदित करती है कि \frac{A D}{D B}=\frac{A E}{B C}
सिद्ध करना है (To Prove): l \| B C
उपपत्ति (Proof):मान लीजिए रेखा l,BC के समान्तर नहीं है तब D से होकर जानेवाली एक अन्य रेखा अवश्य होगी जो BC के समान्तर होगी।मान लीजिए वह रेखा DF है अर्थात् D F \| B C
\because D F \| B C (माना है) अतः आधारभूत आनुपातिकता प्रमेय से
\frac{A D}{D B}=\frac{A F}{FC} \cdots (1) \\ \frac{A D}{D B}=\frac{A E}{E C} \text{ (दिया है) } \cdots(2)
समीकरण (1) व (2) से-
\frac{A F}{F C}=\frac{A E}{E C} \\ \Rightarrow \frac{A F+F C}{F C}=\frac{A E+E C}{E C}(योगानुपात से)
\Rightarrow \frac{A C}{F C}=\frac{A C}{E C} \\ \Rightarrow F C=E C
यह तब ही संभव है जब बिन्दु F,E के संपाती हो।अर्थात् DF स्वयं रेखा l के संपाती हो।
\therefore l \| B C
आधारभूत आनुपातिकता प्रमेय तथा उसके विलोम पर आधारित कुछ और महत्वपूर्ण परिणाम
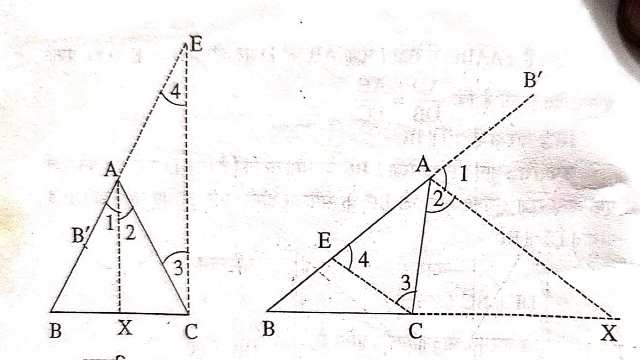
प्रमेय (Theorem):3.त्रिभुज के किसी अंतः कोण या बहिष्कोण का समद्विभाजक,कोण की सम्मुख भुजा को उस कोण को बनाने वाली भुजाओं के अनुपात में अन्त: या बाह्य विभाजित करता है।
उपपत्ति (Proof): XA \| C E तथा AC व B’E तिर्यक रेखाएं हैं
\angle 3=\angle 2 (एकान्तर कोण)…….(1)
तथा \angle 1=\angle 4 (संगत कोण)……(2)
AX, \angle B A C का अर्द्धक है
\therefore \angle 2=\angle 1 (दिया है)….(3)
समीकरण (1),(2) तथा (3) से-
\Rightarrow \angle 3= \angle 4
\triangle AEC के आधार के कोण बराबर हैं
\therefore AE=AC.....(4)
\triangle BCE में AX \parallel CE आधारभूत आनुपातिकता प्रमेय से
\frac{B X}{X C}=\frac{B A}{A E} \\ \Rightarrow \frac{B X}{X C}=\frac{B A}{A C} [(4) से]
प्रमेय (Theorem):4.(प्रमेय (Theorem):3. का विलोम)
यदि किसी त्रिभुज के एक शीर्ष से गुजरने वाली रेखा,शीर्ष के सम्मुख भुजा को,शेष दो भुजाओं के अनुपात में अंत: विभाजित या बाह्य विभाजित करे तो यह रेखा उस शीर्ष पर बने कोण का अन्त: या बाह्य समद्विभाजक होगी।
दिया है (Given):\triangle ABC की भुजा BC पर X बिन्दु आकृति में अन्तर्विभाजित तथा बहिर्विभाजित इस प्रकार करता है कि
\frac{B X}{X C}=\frac{B A}{A C}
सिद्ध करना है (To Prove):\angle B^{\prime} A X=\angle XA C
रचना (Construction):C से AX के समान्तर CE खींचिए जो BA (बढ़ी हुई) को E पर काटे।
उपपत्ति (Proof): \triangle BCE में AX \parallel CE अतः आधारभूत आनुपातिकता प्रमेय से
\frac{B X}{X C}=\frac{B A}{A E}....(1) \\ \frac{B X}{X C}=\frac{B A}{A C} (दिया है)…..(2)
समीकरण (1) व (2) से-
\frac{B A}{A C} =\frac{B A}{A E} \\ \Rightarrow A C =A E
\triangle ACE में AC=AE अतः
\angle 4=\angle 3.....(3)
( \angle 3 तथा \angle 4 त्रिभुज की बराबर भुजा के अभिमुख कोण हैं)
\angle 3=\angle 2 (एकान्तर कोण हैं)…..(4)
समीकरण (3) व (4) से-
\angle 4=\angle 2....(5) \\ \angle 1=\angle 4 (संगत कोण)…..(6)
समीकरण (5) व (6) से-
\angle 1=\angle 2
अर्थात् \angle B^{\prime} A X=\angle X A C
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Loci And Concurrent Lines
2.आधारभूत आनुपातिकता प्रमेय के उदाहरण (Basic Proportionality Theorem Examples),थेल्स प्रमेय के उदाहरण (Thales Theorem Examples)-
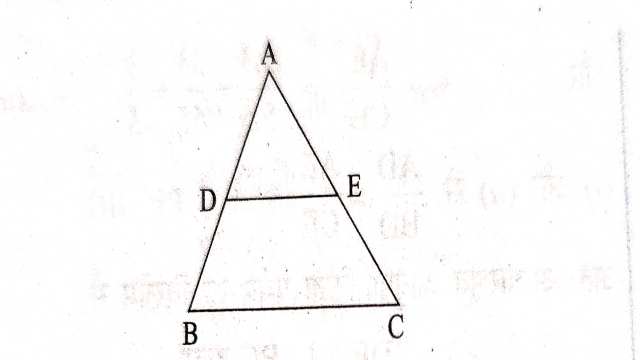
example-1. \triangle ABC की भुजाएं AB व AC पर क्रमशः D व E बिन्दु इस प्रकार स्थित हैं कि DE \parallel BC हो तो
(1.)यदि AD=6 सेमी,DB=9 सेमी और AE=8 सेमी हो तो AC का मान ज्ञात कीजिए।
Solution-प्रश्नानुसार \triangle ABC की भुजाएं AB व AC पर क्रमशः बिन्दु D व E इस प्रकार स्थित हैं कि DE \parallel BC
AD=6 सेमी,BD=9 सेमी,AE=8 सेमी,AC=?
DE \parallel BC अतः आधारभूत आनुपातिकता प्रमेय से
\frac{A D}{B D}=\frac{A E}{C E} \\ \Rightarrow \frac{6}{9}=\frac{8}{E C} \\ \Rightarrow E C=\frac{8 \times 9}{6} \\ EC=12 सेमी
AC=AE+EC \\ \Rightarrow AC=8+12=20 सेमी
(2.)यदि \frac{A D}{D B}=\frac{4}{13} और AC=20.4 सेमी हो तो EC का मान ज्ञात कीजिए।
\frac{A D}{D B}=\frac{4}{13},AC=20.4
माना EC=x,AE=AC-EC
\Rightarrow AE=20.4-x
आधारभूत आनुपातिकता प्रमेय से
\frac{A D}{D B}=\frac{A E}{E C} \\ \frac{4}{13}=\frac{20.4-x}{x} \\ \Rightarrow 4 x=(20.4-x) 13 \\ \Rightarrow 4 x=265.2-13 x \\ \\ \Rightarrow 4 x+13 x=265.2 \\ \Rightarrow 17 x=265.2 \\ \Rightarrow x=\frac{265.2}{17} \\ \Rightarrow x=15.6 सेमी
EC=15.6 सेमी
Example-2. \triangle ABC की भुजाएं AB एवं AC पर क्रमशः D व E दो बिन्दु स्थित हैं,निम्न प्रश्नों में दिए गए मानों के माध्यम से DE \parallel BC होने या न होने की जानकारी दीजिए-
(1.) AB=12 सेमी,AD=8 सेमी,AE=12 सेमी और AC=18 सेमी
Solution-प्रश्नानुसार \triangle ABC की भुजाएं AB व AC पर क्रमशः D व E दो बिन्दु हैं।
AB=12 सेमी,AD=8 सेमी,AE=12 सेमी,AC=18 सेमी
BD=AB-AD
BD=12-8
BD=4 सेमी
CE=AC-AE
CE=18-12
CE=6 सेमी
यहां A D=\frac{8}{4}=\frac{2}{1} \quad \ldots(1)
और A E=\frac{12}{6}=\frac{2}{1} \cdots (2)
समीकरण (1) व (2) से-
\frac{A D}{B D}=\frac{A E}{C E}
अतः आधारभूत आनुपातिकता प्रमेय के विलोम से
DE \parallel BC
(2.)AB=5.6 सेमी,AD=1.4 सेमी,AC=9.0 सेमी तथा AE=1.8 सेमी
Solution-BD=AB-AD=5.6-1.4=4.2 सेमी
CE=AC-AE=9-1.8=7.2 सेमी
यहां \frac{A B}{B D}=\frac{5.6}{4.2}=\frac{4}{3} \ldots(1)
\frac{A E}{C E}=\frac{1.8}{7.2}=\frac{1}{4} \ldots (2)
समीकरण (1) व (2) से-
\frac{A B}{B D} \neq \frac{A E}{CE}
अतः DE,BC के समान्तर नहीं है।
Example-3.दी गई आकृति में OA,OB और OC पर क्रमशः L,M एवं N बिन्दु इस प्रकार स्थित हैं कि LM \parallel AB तथा MN \parallel BC है तो दर्शाइए LN \parallel AC है।
Solution-दिया है (Given): में बिन्दु L,M और N क्रमशः OA,OB और OC पर इस प्रकार स्थित हैं कि LM \parallel AB,MN \parallel BC
सिद्ध करना है (To Prove):LN \parallel AC
उपपत्ति (Proof):\triangle OAB में LM \parallel AB (दिया है)
अतः आधारभूत आनुपातिकता प्रमेय से
\frac{O L}{L A}=\frac{O M}{B M}......(1)
पुनः \triangle OBC में MN \parallel BC (दिया है) अतः आधारभूत आनुपातिकता प्रमेय से
\frac{O M}{B M}=\frac{O N}{N C}....(2)
समीकरण (1) व (2) से-
\frac{O L}{L A}=\frac{O N}{N C}
अतः आधारभूत आनुपातिकता प्रमेय के विलोम से
\triangle OAC में LN \parallel AC
Example-4. \triangle ABC में AB और AC भुजाओं पर क्रमशः D और E बिन्दु इस प्रकार स्थित हैं कि BD=CE हो तो दर्शाइए DE \parallel BC है।
Solution-दिया है (Given): \triangle ABC में AB व AC भुजाओं पर क्रमशः D और E बिन्दु स्थित हैं तथा BD=CE तथा AB=AC
सिद्ध करना है (To Prove):DE \parallel BC
उपपत्ति (Proof):AB=AC (दिया है) ……..(1)
BD=CE (दिया है) ……(2)
समीकरण (1) व (2) से-
\frac{A B}{B D}=\frac{A C}{C E} \\ \Rightarrow \frac{A D}{B D}-1=\frac{A C}{C E}-1 \\ \Rightarrow \frac{A B-B D}{B D}=\frac{A C-C E}{C E} (अन्तरानुपात से)
\Rightarrow \frac{A D}{B D}=\frac{A E}{C E}
अतः आधारभूत आनुपातिकता प्रमेय के विलोम से
DE \parallel BC
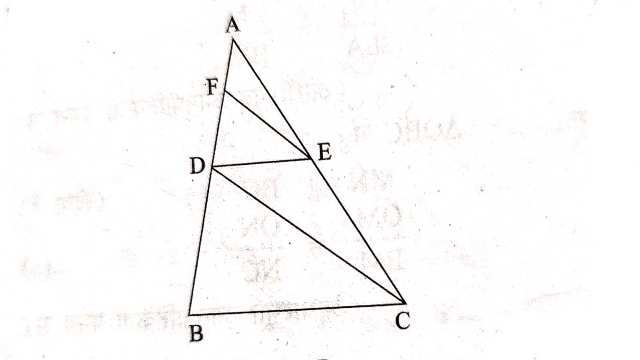
Example-5.आकृति में DE \parallel BC और CD \parallel EF हो तो सिद्ध कीजिए AD^{2}=AB \times AF
Solution-दिया है (Given): DE \parallel BC और CD \parallel EF
सिद्ध करना है (To Prove):AD^{2}=AB \times AF
उपपत्ति (Proof):\triangle ABC में DE \parallel BC (दिया है) अतः आधारभूत आनुपातिकता प्रमेय से-
\frac{A D}{B D}=\frac{A E}{CE}.....(1)
\triangle ABC में CD \parallel EF (दिया है) अतः आधारभूत आनुपातिकता प्रमेय से-
\frac{A F}{FD}=\frac{A E}{CE}....(2)
समीकरण (1) और (2) से
\frac{A D}{B D}=\frac{A F}{F D} \\ \Rightarrow \frac{B D}{A D}=\frac{F D}{A F}(विलोमानुपात से)
\Rightarrow \frac{B D}{A D}+1=\frac{F D}{A F}+1 \\ \Rightarrow \frac{B D+A D}{A D}=\frac{F D+ A F}{A F} (योगानुपात से)
\Rightarrow \frac{A B}{A D}=\frac{A D}{A F} \\ \Rightarrow A D^{2}=A B \times A F
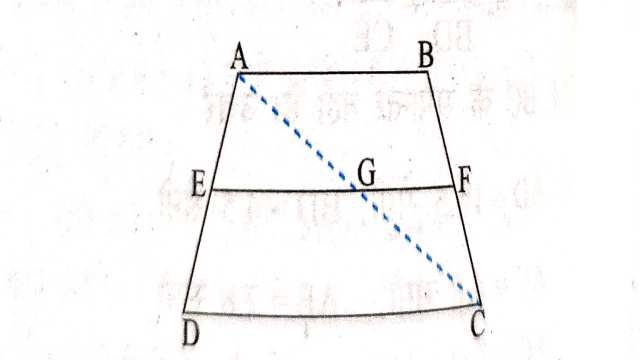
Example-6.आकृति में यदि EF \parallel DC हो तो सिद्ध कीजिए कि \frac{A E}{E D}=\frac{B F}{F C}
Solution-दिया है (Given):EF \parallel DC \parallel AB
सिद्ध करना है (To Prove):\frac{A E}{E D}=\frac{B F}{F C}
रचना (Construction): बिन्दु A और C को जोड़ने पर AC रेखा EF को बिन्दु G पर प्रतिच्छेद करती है।
उपपत्ति (Proof): \triangle ADC में
EG \parallel DC( \because EF \parallel DC) अतः आधारभूत आनुपातिकता प्रमेय से
\frac{AE}{ED}=\frac{AG}{GC}....(1)
इसी प्रकार \triangle CAB में
GF \parallel AB( \because EF \parallel AB) अतः आधारभूत आनुपातिकता प्रमेय से
\frac{C G}{A G}=\frac{C F}{F B} \\ \frac{A G}{C G}=\frac{F B}{C F}(विलोमानुपात से)…..(2)
समीकरण (1) व (2) से-
\frac{AE}{ED}=\frac{BF}{F C}
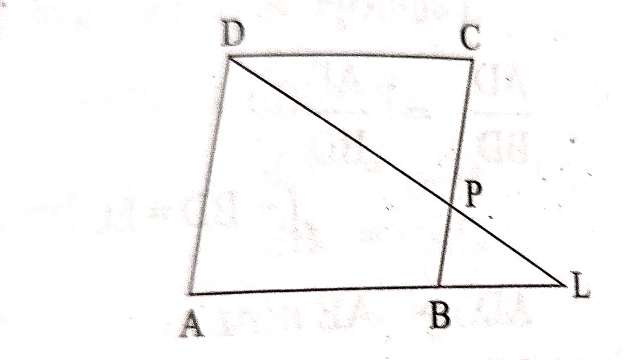
Example-7.ABCD एक समान्तर चतुर्भुज है जिसकी भुजा BC पर कोई बिन्दु P स्थित है।यदि DP एवं AB को आगे बढ़ाएं तो वे L पर मिलते हैं।तो सिद्ध कीजिए-
(1) \frac{D P}{P L}=\frac{D C}{B L} \\ (2) \frac{D L}{D P}=\frac{A L}{D C}
Solution-दिया है (Given):ABCD एक समान्तर चतुर्भुज है।जिसकी भुजा BC पर कोई बिन्दु P स्थित है।DP एवं AB को आगे बढ़ाए तो वे L पर मिलते हैं।
सिद्ध करना है (To Prove):(1) \frac{D P}{P L}=\frac{D C}{B L} \\ (2) \frac{D L}{D P}=\frac{A L}{D C}
उपपत्ति (Proof):ABCD एक समान्तर चतुर्भुज है। अतः DC \parallel AB तथा AD \parallel BC
व AB=CD तथा AD=BC (समान्तर चतुर्भुज के गुणधर्म से)
\triangle LAD में BP \parallel AD[ \because AD \parallel BC]
अतः आधारभूत आनुपातिकता प्रमेय से
\Rightarrow \frac{B L}{A B}=\frac{L P}{P D} ....(1)\\ \Rightarrow \frac{B L}{D C}=\frac{P L}{D P}[\because AB=CD] \\ \Rightarrow \frac{D P}{P L}=\frac{D C}{B L}(विलोमानुपात से)
पुनः \frac{P L}{D P}=\frac{B L}{D C} \\ \Rightarrow \frac{P L}{D P}=\frac{B L}{A B}[\because D C=A B] \\ \Rightarrow \frac{P L}{D P}+1=\frac{B L}{A B} +1\\ \Rightarrow \frac{P L+D P}{D P}=\frac{B L+A B}{A B}(योगानुपात से)
\Rightarrow \frac{D L}{D P}=\frac{A L}{A B} \\ \Rightarrow \frac{D L}{D P}=\frac{A L}{D C}[\because A B=D C]
Example-8. \triangle ABC की भुजा AB पर D और E दो ऐसे बिन्दु स्थित हैं कि AD=BE हो।यदि DP \parallel BC तथा EQ \parallel AC हो तो सिद्ध कीजिए कि PQ \parallel AB है।
Solution-दिया है (Given):\triangle ABC की भुजा AB पर D और E बिन्दु स्थित हैं।तथा AD=BE व DP \parallel BC एवं EQ \parallel AC
सिद्ध करना है (To Prove):PQ \parallel AB
उपपत्ति (Proof):\triangle ABC में DP \parallel BC अतः आधारभूत आनुपातिकता प्रमेय से
\frac{A D}{D B}=\frac{A P}{P C}....(1)
इसी प्रकार E Q \| A C \\ \frac{B E}{E A}=\frac{B Q}{Q C}.....(2)
EA=AD+DE \\ \Rightarrow EA=BE+DE ( \because AD=BE)
\Rightarrow EA=BD ,(2) में रखने पर
\Rightarrow \frac{A D}{B D}=\frac{B Q}{Q C}
समीकरण (1) व (3) से-
\frac{A P}{P C}=\frac{B Q}{Q C}
अतः आधारभूत आनुपातिकता प्रमेय के विलोम से PQ \parallel AB
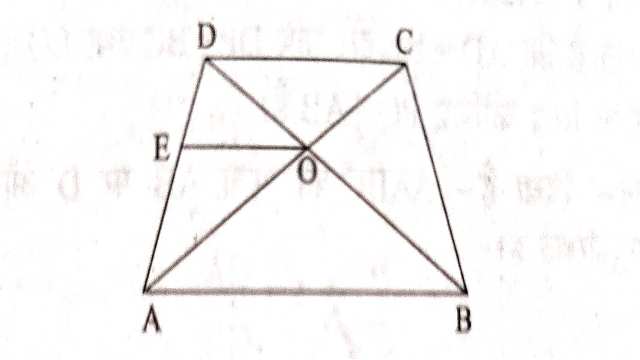
Example-9.ABCD एक समलम्ब चतुर्भुज है जिसकी भुजा AB \parallel DC है तथा इसके विकर्ण O पर प्रतिच्छेद करते हैं।दर्शाइए \frac{A O}{BO} =\frac{C O}{DO} है।
Solution-दिया है (Given):ABCD एक समलम्ब चतुर्भुज है जिसमें AB \parallel DC है।विकर्ण AC तथा BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove):\frac{A O}{BO} =\frac{C O}{DO}
रचना (Construction): बिन्दु O से EO \parallel DC \parallel AB खींची।
उपपत्ति (To Prove): \triangle DAB में EO \parallel AB(रचना से)
अतः आधारभूत आनुपातिकता प्रमेय से-
\frac{D E}{EA} =\frac{D O}{O B}......(1)
पुनः \triangle DCA में EO \parallel DC (रचना से) अतः आधारभूत आनुपातिकता प्रमेय से-
\frac{D E}{EA} =\frac{C O}{O A}.....(2)
समीकरण (1) व (2) से-
\frac{D O}{O B} =\frac{C O}{O A} \\ \Rightarrow \frac{O A}{B O} =\frac{C O}{D O}
3.आधारभूत आनुपातिकता प्रमेय की समस्याएं (Basic Proportionality Theorem Problems),थेल्स प्रमेय की समस्याएं (Thales Theorem Problems)-
उपर्युक्त उदाहरणों के द्वारा आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem) को समझ सकते हैं।
(1.)\triangle ABC की भुजाएं AB व AC पर क्रमशः D व E बिन्दु इस प्रकार स्थित हैं कि DE \parallel BC हो तो
(i)यदि \frac{AD}{DB}=\frac{7}{4} और AE=6.3 सेमी हो तो AC का मान ज्ञात कीजिए।
(ii) यदि AD=4x-3,AE=8x-7,BD=3x-1 और CE=5x-3 हो तो x का मान ज्ञात कीजिए।
(2.)यदि \triangle ABC की भुजाएं AB एवं AC पर क्रमशः D व E दो बिन्दु स्थित हैं, निम्न प्रश्नों में दिए गए मानों के माध्यम से DE \parallel BC होने या न होने की जानकारी दीजिए।
(i)AB=5.6 सेमी,AD=1.4 सेमी,AC=9.0 सेमी तथा AE=1.8 सेमी
(ii)AD=5.7 सेमी,BD=9.5 सेमी,AE=3.3 सेमी तथा EC=5.5 सेमी
(3.)यदि D और E क्रमशः AB और AC, त्रिभुज ABC की भुजाओं पर स्थित ऐसे बिन्दु हैं कि BD=CE तथा DE \parallel BC हो तो सिद्ध कीजिए \triangle ABC एक समद्विबाहु त्रिभुज है।
Answers):(1.)(i)AC=9.9 सेमी (ii)x=1
(2)(i) DE \not \parallel BC (ii)DE \parallel BC
उपर्युक्त सवालों को हल करने पर आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem) को समझ सकते हैं।
उपर्युक्त उदाहरणों के द्वारा आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem) को समझ सकते हैं।
(1.)\triangle ABC की भुजाएं AB व AC पर क्रमशः D व E बिन्दु इस प्रकार स्थित हैं कि DE \parallel BC हो तो
(i)यदि \frac{AD}{DB}=\frac{7}{4} और AE=6.3 सेमी हो तो AC का मान ज्ञात कीजिए।
(ii) यदि AD=4x-3,AE=8x-7,BD=3x-1 और CE=5x-3 हो तो x का मान ज्ञात कीजिए।
(2.)यदि \triangle ABC की भुजाएं AB एवं AC पर क्रमशः D व E दो बिन्दु स्थित हैं, निम्न प्रश्नों में दिए गए मानों के माध्यम से DE \parallel BC होने या न होने की जानकारी दीजिए।
(i)AB=5.6 सेमी,AD=1.4 सेमी,AC=9.0 सेमी तथा AE=1.8 सेमी
(ii)AD=5.7 सेमी,BD=9.5 सेमी,AE=3.3 सेमी तथा EC=5.5 सेमी
(3.)यदि D और E क्रमशः AB और AC, त्रिभुज ABC की भुजाओं पर स्थित ऐसे बिन्दु हैं कि BD=CE तथा DE \parallel BC हो तो सिद्ध कीजिए \triangle ABC एक समद्विबाहु त्रिभुज है।
Answers):(1.)(i)AC=9.9 सेमी (ii)x=1
(2)(i) DE \not \parallel BC (ii)DE \parallel BC
उपर्युक्त सवालों को हल करने पर आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem) को समझ सकते हैं।
अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.थेल्स प्रमेय कक्षा 10 क्या है? (What is Thales Theorem Class 10?)-
उत्तर:आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem) को थेल्स प्रमेय (Thales Theorem) भी कहते हैं।क्योंकि थेल्स (लगभग 600 ई.पू.) जिन्होंने यूनान में ज्यामिति के अध्ययन की शुरुआत की,ने समरूप त्रिभुजों से सम्बद्ध एक महत्त्वपूर्ण तथ्य को सिद्ध किया था। इतिहासकारों के कथनानुसार थेल्स ने मिश्र में एक पिरैमिड की छाया की लम्बाई ज्ञात करके उस पिरैमिड की ऊंचाई ज्ञात की थी।
थेल्स प्रमेय कथन
यदि एक त्रिभुज की एक भुजा के समानांतर एक रेखा खींची जाती है,जो अन्य दो भुजाओं को अलग-अलग बिंदुओं में काटती है, तो अन्य दो भुजाएँ समान अनुपात में विभाजित होती हैं।
प्रश्न:2.थेल्स प्रमेय का विलोम क्या है? (What is converse Thales Theorem?)-
उत्तर:आधारभूत आनुपातिकता प्रमेय का विलोम: यदि कोई रेखा त्रिभुज के किसी भी दो भुजाओं को समान अनुपात में विभाजित करती है, तो रेखा को तीसरी भुजा के समानांतर होना चाहिए।
प्रश्न:3.थेल्स प्रमेय क्यों महत्वपूर्ण है? (Why is Thales theorem important?)-
उत्तर:थेल्स ऑफ़ मिलेटस को 5 ज्यामितीय प्रमेयों की खोज का श्रेय दिया जाता है: एक वृत्त इसके व्यास द्वारा द्विभाजित होता है।एक त्रिभुज के दो बराबर भुजा के विपरीत कोण बराबर हैं।हम एक त्रिभुज निर्धारित कर सकते हैं यदि हमारे पास इसके आधार की लंबाई है और आधार पर दो कोण दिए गए हैं।
थेल्स ने समरूप त्रिभुजों के बारे में महत्त्वपूर्ण दिया था।इस गुण का उपयोग डिजाइन इंजीनियर और आर्किटेक्ट किया करते हैं।किसी भवन या कलपुर्जों का किसी पैमाने के हिसाब से समरूप डिजाइन बनाते हैं जो आकार (Size) में भवन या कलपुर्जे से काफी छोटा होता है,ठेकेदार या कारीगर उसे समझकर सही-सही भवन निर्माण कर लेता है।
प्रश्न:4.आधारभूत आनुपातिक प्रमेय से आपका क्या अभिप्राय है? (What do you mean by Basic Proportionality Theorem?)-
उत्तर:आधारभूत आनुपातिकता प्रमेय (BPT बीपीटी के रूप में संक्षिप्त किया जा सकता है) में कहा गया है कि,यदि एक रेखा एक त्रिभुज की एक भुजा के समानांतर है जो अन्य भुजाओं को दो अलग-अलग बिंदुओं में विभाजित करती है, तो रेखा उन भुजाओं को समान अनुपात में विभाजित करती है।
उपर्युक्त प्रश्नों के उत्तर, उदाहरणों तथा सवालों को हल करने पर आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem) को ठीक से समझ सकते हैं।
उपर्युक्त प्रश्नों के उत्तर, उदाहरणों तथा सवालों को हल करने पर आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem),थेल्स प्रमेय (Thales Theorem) को ठीक से समझ सकते हैं।
Also Read This Article:-Height and Distance in Trigonometry
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
