Symmetry in Mathematics
1.गणित में सममिति (Symmetry in Mathematics),सममिति (Symmetry):
- गणित में सममिति (Symmetry in Mathematics) की जीवन में महत्त्वपूर्ण उपयोगिता है।किसी पेड़ पर लगी पत्तियों,फूलों की पंखुड़ियों में सममिति को देख सकते हैं।विभिन्न ज्यामितीय आकृतियों जैसे कि त्रिभुज,वर्ग,पंचभुज,षट्भुज या वृत्त आदि से हम भली-भांति परिचित हैं।प्रकृति प्रदत्त इन सभी आकृतियों में सममिति को देख सकते हैं।प्रकृति द्वारा निर्मित तथा मानव द्वारा निर्मित विभिन्न प्रकार की आकृतियों में हमें सममिति दिखाई दे जाएगी। किसी भी आकृति के हिस्सों की किसी रेखा या बिन्दु के संदर्भ में सर्वांगसमता को ही सममिति का नाम दिया जाता है।
- किसी भी पेड़ के पत्ते के केंद्र बिंदु तथा उसके शीर्ष से होकर गुजरने वाली ऊर्ध्वाधर रेखा के सापेक्ष सममितीय है।इस आकृति को किसी कोण से घुमाने पर यह अपरिवर्तित रहती है।अतः इस प्रकार की आकृति में अक्षीय एवं घूर्णीय दोनों तरह की सममितियां मौजूद है।
- प्रकृति के कई अन्य वस्तुओं में भी सममिति देखने को मिलती है।साधारण नमक के क्रिस्टल को ले लें।वे घनाकार हैं।घन एक ऐसी वस्तु का प्रतीक है जिसमें बहुअक्षीय सममिति मौजूद है।विषमलंबक्ष गंधक का क्रिस्टल (crystal of heterotrophic sulphur) सममितीय क्रिस्टल का एक अन्य दृष्टांत है।
चतुष्फलक एक अन्य सममितीय आकृति है।नगों में बेशकीमती हीरा कार्बन परमाणुओं द्वारा रचित चतुष्फलकीय जालक का एक अन्य उदाहरण क्वार्ट्ज है।
- प्रकृति में स्थित एक अन्य आकृति है षट्भुज।जहां एक ओर कार्बन परमाणुओं का चतुष्फलकीय जालक हीरे को पदार्थों में कठोरतम स्वरूप करता है,वहीं दूसरी ओर एक तल में अवस्थित कार्बन परमाणुओं की षट्भुजीय व्यवस्था ग्रेफाइट की मणियों को चिकनापन प्रदान करती है और उसे गुरुकार्य (हेवी ट्यूटी) मशीनों के लिए एक आदर्श स्नेहक बनाती है।शहद के छत्तों के खानों का षट्भुजीय आकार उसे सर्वोत्तम समष्टि-पूरक (स्पेस फिलिंग) आकृति बनाता है।
- संभवतया प्रकृति को सर्वाधिक प्यारी अहम् सर्पिल आकृति या ‘हेलिक्स’ नुमा ज्यामिति आकृति है हालांकि यह पूरी तरह से सममितीय नहीं है।हेलिक्स एक ऐसा वक्र है जो स्वयं को एक बेलन पर लपेटती जाती है।पेंच हेलिक्स इसका एक उदाहरण है।किसी वृक्ष पर चढ़ती लता या स्प्रिंग के लिपटते प्रतान (ट्रेंडिल) को भी प्रकृति में हेलिक्स के दृष्टांत के रूप में देखा जा सकता है।किसी भी कोशिका के केंद्रक में स्थित डीएनए का अणु जो नंगी आंख से दिखाई नहीं पड़ता,भी दोहरी सर्पिलाकृति द्वारा निर्मित है।इस दोहरी सर्पिलाकृति की हर भुजा न्यूक्लियोटाइडों की एक लंबी श्रृंखला द्वारा निर्मित होती है जिसमें एक शर्करा का अणु,एक फास्फेट व एक नाइट्रोजन के आधारवाला अणु मौजूद होता है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Symbols in Mathematics
(1.)ज्यामिति में सममिति (Symmetry in Geometry):
- ज्यामिति में सममिति एक महत्वपूर्ण टॉपिक है। अनेक ज्यामितीय आकृतियां किस बिंदु या रेखा के सममित होती हैं।इन आकृतियों की बनावट में हम सममिति देखकर या तुलना कर कोई त्रुटि निकाल सकते हैं।
सममिति कला में अत्यंत महत्वपूर्ण भूमिका अदा करती है।सममिति की सहायता से कलाकार सुंदर डिजाइनें बनाता है।ऐतिहासिक इमारतों में ताजमहल सममिति का एक अद्वितीय उदाहरण है।तितली,मनुष्य आदि सममिति के अन्य उदाहरण हैं।रंगोली की डिजाइनें भी सममिति के उदाहरण हैं।
सममिति कई प्रकार की होती है।बिंदु के सापेक्ष सममिति,रेखा के सापेक्ष सममिति,तल के सापेक्ष सममिति,घूर्णन सममिति आदि।
Also Read This Article:Development of Modern Mathematics
(2.)सममित आकृतियां (Symmetrical Shapes):
- ऐसी ज्यामितीय आकृतियां को जो किसी रेखा या बिंदु के दोनों ओर समान रूप से बनी है,उन्हें सममितीय आकृतियां कहते हैं।
(i)दर्पण पट्टिका की सहायता से सममिति ज्ञात करना (Find Symmetry with the help of Mirror Plate):
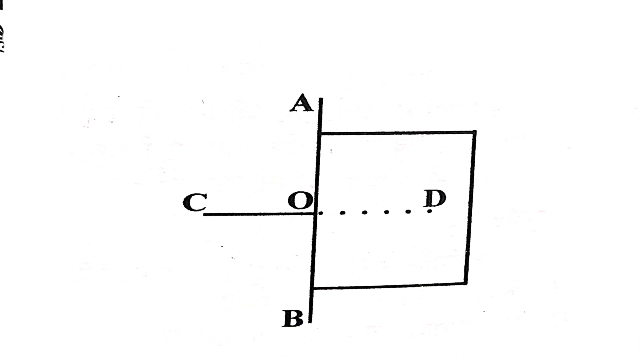
- एक दर्पण पट्टिका को शीर्ष बिंदु A से होते हुए इस प्रकार मिलाकर रखो कि चित्र के एक ओर का भाग तथा उसका दर्पण पट्टिका में प्रतिबिंब मिलाकर त्रिभुज ABC की पूरी आकृति बन जाए।इस प्रकार Ay रेखा के दाहिनी ओर का भाग उसके बाएं ओर के भाग का प्रतिबिंब है।चित्र में Ay सममित रेखा है।
- दर्पण ABC में C का प्रतिबिंब D बिंदु है।यदि दो बिंदु एक रेखा के सापेक्ष सममित हों तो वे उस रेखा में एक-दूसरे के दर्पण प्रतिबिंब हैं।रेखा AB के सापेक्ष,C,D सममित है तथा D,C सममित हैं।
- परिभाषा:दो आकृतियाँ एक दी हुई रेखा के सापेक्ष सममित होती है यदि वह रेखा में एक दूसरे के दर्पण प्रतिबिंब हों।तब यह रेखा सममित रेखा या सममिति अक्ष कहलाती है।
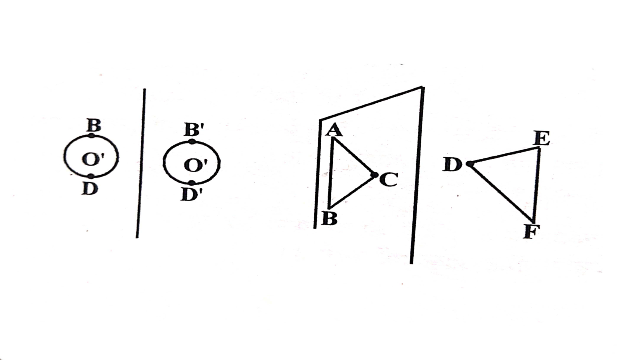
- यदि चित्र में हम ∆ABC की किसी भुजा पर कोई बिंदु P लें तो उसका सममित बिंदु Q,∆DEF की संगत भुजा पर स्थित होगा।सममिति आकृतियों के युग्म,सममिति बिंदुओं के युग्म के बने होते हैं।सममित आकृतियों के युग्म विपरीत सर्वांगसम होते हैं।
- चित्र ABCD एक वर्ग है तथा P,Q,R तथा S वर्ग की भुजाओं के क्रमशः मध्य बिंदु हैं।
यदि हम वर्ग को RP पर मोड़े तो आयत PBCR तथा आयत APRD संपाती हो जाते हैं।
- इस प्रकार आयत PBCR तथा आयत APRD ,रेखा RP के सापेक्ष आयतों का एक सममित युग्म है।
वर्ग ABCD,रेखा RP के सापेक्ष सममित है जो सम्मुख भुजाओं के एक युग्म के मध्य बिंदुओं को मिलाती है।
वर्ग ABCD,रेखा SQ के सापेक्ष भी सममित है। - इस प्रकार एक रेखा किसी आकृति को दो सर्वांगसम भागों में विभाजित कर सकती है परंतु वह सममित अक्ष केवल तभी होगी जबकि दोनों भाग रेखा में एक-दूसरे में दर्पण प्रतिबिंब हों।
- समबाहु त्रिभुज:त्रिभुज में समबाहु त्रिभुज XYZ को हम देखा XP पर मोड़ दें तो हम देखेंगे कि बिंदु Y का प्रतिबिंब है।समद्विबाहु त्रिभुज XYZ,रेखा XP के सापेक्ष सममित है।
- वृत्त के सममित रेखाएं वृत्त के केंद्र से जानेवाली रेखा पर वृत्त को मोड़े तो वृत्त का एक भाग व्यास के दूसरी ओर के भाग को ढक लेगा।हम O बिंदु में से होकर अनंत रेखाएं खींच सकते हैं।अतः वृत्त के केंद्र में होकर गुजरती हुई रेखा (व्यास) वृत्त की सममित रेखा होती है।
- अतः (तल में) में कोई ज्यामितीय आकृति सममित तल कहलाती है जबकि (तल में) कोई ऐसी रेखा ज्ञात हो सकती है जो इस आकृति को दो सर्वांगसम भागों में विभाजित करें तथा प्रत्येक भाग में एक-दूसरे का दर्पण प्रतिबिंब हो जाए।अब आकृति को इस रेखा के सापेक्ष सममित कहा जाता है तथा रेखा सममिति अक्ष कहलाती है।
- स्टीवर्ट ने अपनी पुस्तक ‘Concepts of Modern Mathematics’ में लिखा है:
- “प्रकृति में अनेक प्रकार की सममित आकृतियां विद्यमान है जिन्हें प्राचीनकाल से पहचाना जाता रहा है।मनुष्य की आकृति लंबवत रेखा (अधिक उपर्युक्त लम्बवत् तल) के सापेक्ष लगभग सममित है)।इसी कारण दर्पण में बाएं और दाएं के प्रतिबिंब परस्पर प्रतिवर्ती रूप से परिवर्तित हो जाते हैं।इस प्रकार की सममिति को द्वि-पक्षी सममिति कहते हैं।”
- कोई भी आकृति एक साथ अनेक रेखाओं के सापेक्ष सममिति हो सकती है या द्वि-पक्षी तथा घूर्णन सममिति का मिश्रण हो सकती है।एक वर्ग अपने विकर्णों के तथा केन्द्र में होती हुई भुजाओं के समांतर रेखाओं के सापेक्ष सममिति होता है।इसे 90 डिग्री पर घुमाया जा सकता है।
- सममिति की संकल्पना में गूढ़ विचार यह है कि आकृतियों को चारों ओर घुमाया जा सकता है तथा फिर भी यह वैसी की वैसी बनी रहती है।कतिपय बिंदु,यह आवश्यक नहीं है कि वे एक ही स्थान पर रहें।यदि हम एक वर्ग ABCD को केंद्र के सापेक्ष एक समकोण पर घूमाएं तो बिंदु A घूमता है B तक,B घूमता है C तक,C घूमता है D तक तथा D घूमता है A तक।
- निम्न आकृतियाँ असममित हैं:
- उपर्युक्त आकृतियों में सममित अक्ष नहीं है क्योंकि हम इन आकृतियों को किसी भी रेखा पर मोड़ें तो प्रतिबिम्ब युग्म प्राप्त नहीं होते हैं।
- उपर्युक्त विवरण में गणित में सममिति (Symmetry in Mathematics),सममिति (Symmetry) के बारे में बताया गया है।
2.गणित में सममिति (Symmetry in Mathematics),सममिति (Symmetry) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.गणित में सममिति क्या है? (What is Symmetry in Mathematics?):
उत्तर:रोजमर्रा की भाषा में सममिति सामंजस्यपूर्ण और सुंदर अनुपात और संतुलन की भावना को संदर्भित करता है। गणित में, “सममिति (symmetry)” में अधिक सटीक परिभाषा होती है और आमतौर पर एक वस्तु को संदर्भित करने के लिए उपयोग किया जाता है जो कुछ परिवर्तनों के तहत अपरिवर्तनीय है; अनुवाद (translation), प्रतिबिंब (reflection),रोटेशन (rotation) या स्केलिंग (scaling) सहित।
प्रश्न:2.गणित में सममिति का क्या मतलब है? (What does symmetry mean in math?):
उत्तर:कुछ सममित है जब यह दोनों पक्षों पर एक ही है।एक आकार में सममिति होती है यदि उस पर एक केंद्रीय विभाजन रेखा (दर्पण रेखा) तैयार की जा सकती है,तो यह दिखाने के लिए कि आकार के दोनों पहलू बिल्कुल समान हैं।
प्रश्न:3.क्या सममिति ज्यामिति का हिस्सा है? (Is symmetry part of geometry?):
उत्तर:ज्यामिति में,किसी वस्तु में सममिति होती है यदि कोई ऑपरेशन या परिवर्तन (जैसे अनुवाद, स्केलिंग,रोटेशन या प्रतिबिंब (such as translation, scaling, rotation or reflection)) होता है जो आकृति/वस्तु को स्वयं पर मैप करता है (यानी, वस्तु में ट्रांसफॉर्म के तहत एक भिन्नता होती है)। इस प्रकार, एक सममिति को बदलने के लिए प्रतिरक्षा के रूप में सोचा जा सकता है।
प्रश्न:4.समरूपता के 5 प्रकार क्या हैं? (What are the 5 types of symmetry?):
उत्तर:पहचान (Identity),प्रतिबिंब (Reflection),उलटा (Inversion),उचित रोटेशन (Proper Rotation) और अनुचित रोटेशन (Improper Rotation) सहित सममिति आपरेशनों के पांच प्रकार के होते हैं ।
प्रश्न:5.गणित में सममिति महत्वपूर्ण क्यों है? (Why is symmetry important in math?):
उत्तर:सममिति ज्यामिति,प्रकृति और आकृतियों का एक मौलिक हिस्सा है।यह पैटर्न बनाता है जो हमें हमारी दुनिया को संकल्पनात्मक रूप से व्यवस्थित करने में मदद करता है।
गणित ग्रेड 3-5 के शिक्षकों की राष्ट्रीय परिषद के अनुसार परिवर्तनों को लागू करने और गणितीय स्थितियों का विश्लेषण करने के लिए सममिति का उपयोग करने में सक्षम होना चाहिए।
उपर्युक्त प्रश्नों के उत्तर द्वारा गणित में सममिति (Symmetry in Mathematics),सममिति (Symmetry) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Symmetry in Mathematics
गणित में सममिति (Symmetry in Mathematics)
Symmetry in Mathematics
गणित में सममिति (Symmetry in Mathematics) की जीवन में महत्त्वपूर्ण उपयोगिता है।किसी पेड़ पर लगी पत्तियों,फूलों की पंखुड़ियों में सममिति को देख सकते हैं।विभिन्न ज्यामितीय आकृतियों जैसे कि त्रिभुज,वर्ग,पंचभुज,षट्भुज या वृत्त आदि से हम भली-भांति परिचित हैं।प्रकृति प्रदत्त इन सभी आकृतियों में सममिति को देख सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
