1.समान्तर चतुर्भुज के गुणधर्म (Properties of Parallelogram)-

समान्तर चतुर्भुज के गुणधर्मो (Properties of Parallelogram) का अध्ययन करने के लिए हमें कुछ परिभाषाओं का अध्ययन करना होगा।
(1.)चतुर्भुज (Quadrilateral):
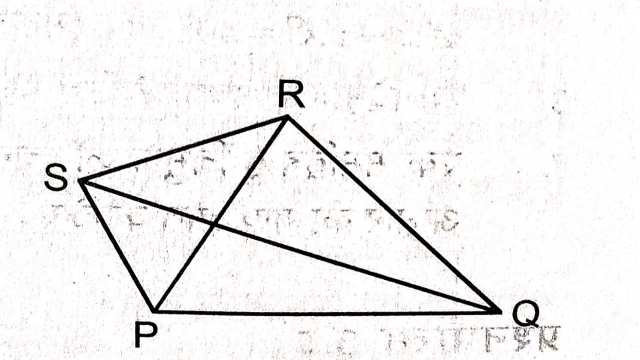
चार भुजाओं से घिरी हुई आकृति को चतुर्भुज कहते हैं।एक चतुर्भुज में चार भुजाएं,चार कोण एवम् चार शीर्ष होते हैं।जैसा कि चित्र में चतुर्भुज PQRS में PQ,QR,RS तथा SP चार भुजाएं P,Q,R तथा S चार शीर्ष \angle P,\angle Q,\angle R \text { तथा } \angle S तथा शीर्षों पर बने कोण हैं।

सम्मुख भुजाएं एवं सम्मुख कोण-चित्र में भुजा PQ की सम्मुख भुजा RS तथा PS की सम्मुख भुजा QR है। \angle P का सम्मुख \angle R तथा \angle Q का सम्मुख \angle S है।
चित्र में आसन्न भुजाओं के युग्म PQ,QR तथा PS,SR है।इसी प्रकार SP,PQ तथा SR,RQ भुजा युग्म आसन्न भुजा युग्म है।
विकर्ण-सम्मुख शीर्षों को मिलाने वाले रेखाखण्ड शीर्ष कहलाते हैं।
चतुर्भुज के प्रकार (Types of Quadrilateral)-
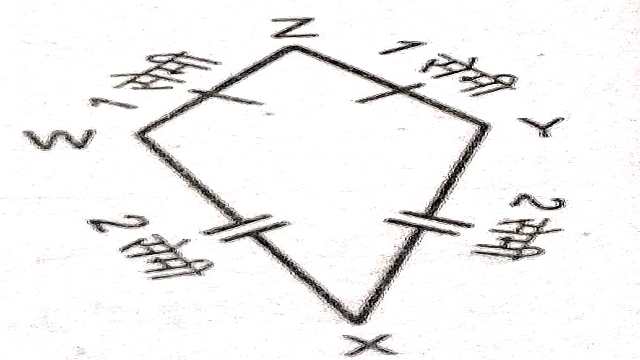
(2.)पतंग (Kite)-
चित्र में WXYZ यह एक ऐसा चतुर्भुज है जिसकी आसन्न भुजाओं के दो युग्म अर्थात् WX,XY तथा WZ,YZ बराबर हैं,पतंग है।अर्थात् ऐसा चतुर्भुज जिसकी आसन्न भुजाओं के कोई दो युग्म बराबर हो,पतंग के नाम से जानते हैं।

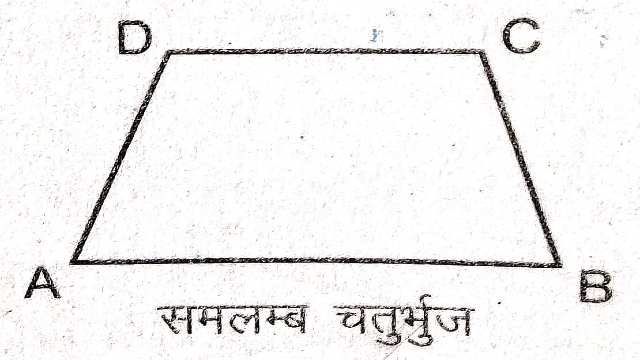
(3.)समलम्ब चतुर्भुज (Trapezium)-
चतुर्भुज ABCD की सम्मुख भुजाओं का एक युग्म AB और DC समान्तर है।इस चतुर्भुज को समलम्ब चतुर्भुज के नाम से जानते हैं।अर्थात् ऐसा चतुर्भुज जिसकी सम्मुख भुजाओं का एक युग्म समान्तर हो, समलम्ब चतुर्भुज कहलाता है।

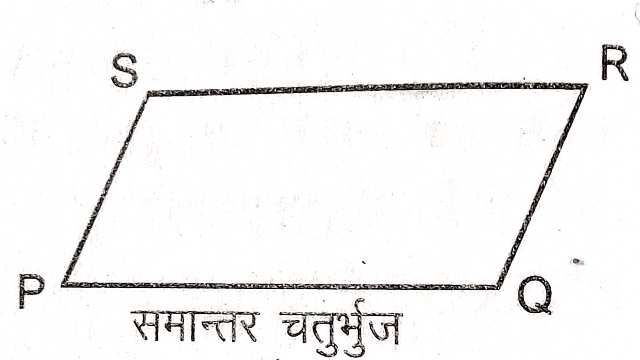
(4.)समान्तर चतुर्भुज (Parallelogram)-
चित्र में PQRS एक समान्तर चतुर्भुज है जिसकी सम्मुख भुजाओं के दोनों युग्म PQ,RS तथा PS,QR समान्तर है।इस चतुर्भुज को समान्तर चतुर्भुज के नाम से जानते हैं।
अर्थात् ऐसा चतुर्भुज जिसकी सम्मुख भुजाओं के दोनों युग्म समान्तर होते हैं।
एक समान्तर चतुर्भुज एक समलम्ब चतुर्भुज है,परन्तु एक समलम्ब चतुर्भुज समान्तर चतुर्भुज नहीं है।

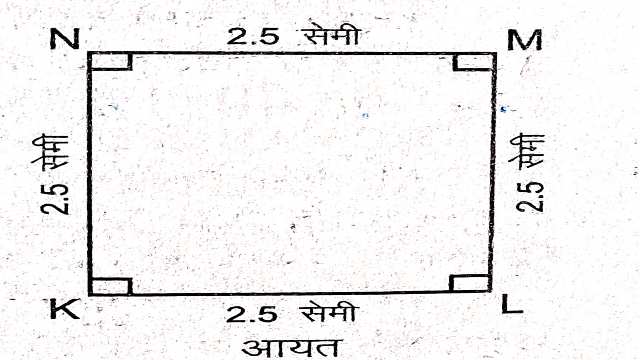
(5.)आयत (Rectangular)-
चित्र में EFGH एक विशेष समान्तर चतुर्भुज “आयत” है जिसका प्रत्येक कोण 90° होता है।अर्थात् ऐसा समान्तर चतुर्भुज जिसका प्रत्येक कोण समकोण हो,आयत के नाम से जानते हैं।
एक आयत एक समान्तर चतुर्भुज है परन्तु एक समान्तर चतुर्भुज एक आयत है यह आवश्यक नहीं है।

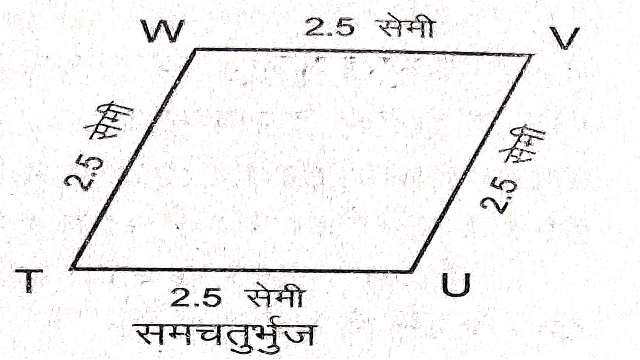
(6.) समचतुर्भुज (Rhombus)-
चित्र में TUVW एक विशेष समान्तर चतुर्भुज “समचतुर्भुज” है जिसकी प्रत्येक भुजा का माप बराबर है।अर्थात् ऐसा समान्तर चतुर्भुज जिसकी प्रत्येक भुजा समान नाप की हो को समचतुर्भुज के नाम से जानते हैं।
एक समचतुर्भुज एक समान्तर चतुर्भुज है परन्तु एक समान्तर चतुर्भुज एक समचतुर्भुज है यह आवश्यक नहीं है।
एक समचतुर्भुज एक समलम्ब चतुर्भुज है परन्तु एक समलम्ब चतुर्भुज समचतुर्भुज नहीं है।

(7.)वर्ग (Square)-
KLMN एक विशेष आयत “वर्ग” है जिसकी प्रत्येक भुजा बराबर है।अथवा एक विशेष समान्तर चतुर्भुज जिसकी प्रत्येक भुजा बराबर एवं प्रत्येक कोण 90° है।अर्थात् ऐसा आयत जिसकी प्रत्येक भुजा बराबर है,वर्ग के नाम से जानते हैं।एक वर्ग,एक समलम्ब चतुर्भुज है परन्तु एक समलम्ब चतुर्भुज वर्ग नहीं है।
एक वर्ग समान्तर चतुर्भुज है परन्तु एक समान्तर चतुर्भुज वर्ग है यह आवश्यक नहीं है।
एक वर्ग एक आयत है परन्तु एक आयत एक वर्ग है यह आवश्यक नहीं है।
एक वर्ग एक समचतुर्भुज है परन्तु एक समचतुर्भुज एक वर्ग है यह आवश्यक नहीं है।

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Inequalities of triangle class 9

2.समान्तर चतुर्भुज के गुणधर्म (Properties of Parallelogram)-

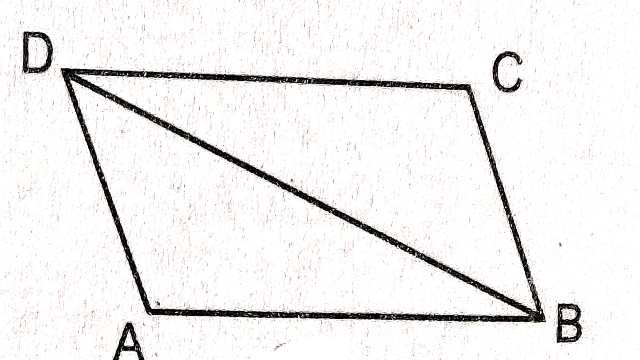
प्रमेय (Theorem):1.किसी समान्तर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
दिया है (Given):ABCD एक समान्तर चतुर्भुज है और BD उसका विकर्ण है।

सिद्ध करना है (To Prove):\triangle ABD \cong \triangle CDB
उपपत्ति (Proof):चित्र में ABCD एक समान्तर चतुर्भुज है AB \parallel CD एवं BD एक तिर्यक रेखा है तो
\angle ABD=\angle BDC (एकान्तर कोण)……(1)
AD \parallel BC, BD तिर्यक रेखा है तो
\angle ADB=\angle DBC(एकान्तर कोण)…..(2)
\triangle ABD व \triangle CDB में
\angle ABD=\angle BDC[(1)से]
BD=BD(उभयनिष्ठ भुजा)
\angle ADB=\angle DBC[(2) से]
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By SAS Property)

\Rightarrow \triangle ABD \cong \triangle CDB
प्रमेय (Theorem):2.समान्तर चतुर्भुज की सम्मुख भुजाएं बराबर होती है।

दिया है (Given):चित्र में ABCD एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):AB=CD एवं AD=BC
रचना (Construction):BD एक विकर्ण खींचिए।
उपपत्ति (Proof):\triangle ABD व \triangle CDB में
\angle ABD=\angle BDC(एकान्तर कोण)
BD=BD(उभयनिष्ठ भुजा)
\angle ADB=\angle DBC(एकान्तर कोण)
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Property)

\Rightarrow \triangle ABD \cong \triangle CDB
AB=CD एवं AD=BC
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
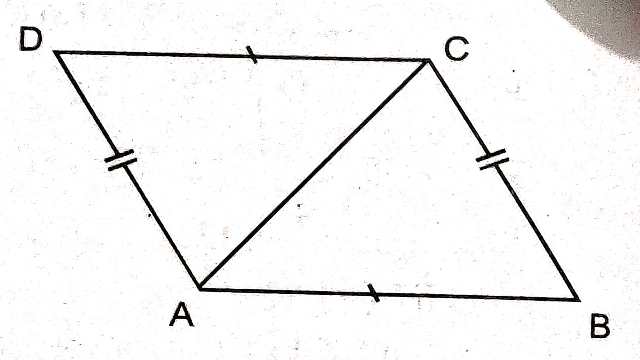
प्रमेय (Theorem):3.(प्रमेय 2 का विलोम) किसी चतुर्भुज की सम्मुख भुजाओं का युग्म समान हो तो वह समान्तर चतुर्भुज होता है।

दिया है (Given):ABCD एक चतुर्भूज है जिसकी सम्मुख भुजाएं AB=CD एवं BC=AD है।
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
रचना (Construction):Aव C को मिलाया।
उपपत्ति (Proof):\triangle ABC व \triangle CDA में
AB=CD (दिया है)
BC=AD (दिया है)
AC=AC (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Property)

\triangle ABC \cong \triangle CDA
अर्थात् \angle CAB=\angle ACD(एकान्तर कोण)

\Rightarrow  AB \parallel CD….(1)
एवं \angle ACB=\angle CAD(एकान्तर कोण)

\Rightarrow BC=AD…….(2)
(1),(2) से चतुर्भुज ABCD एक समान्तर चतुर्भुज है।
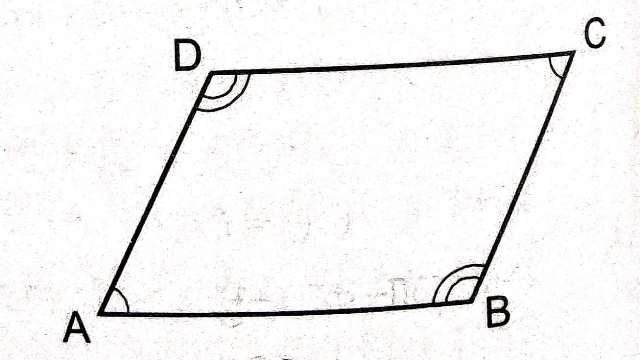
प्रमेय (Theorem):4.समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।

दिया है (Given):ABCD एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):\angle A=\angle C,\angle B=\angle D
उपपत्ति (Proof):ABCD एक समान्तर चतुर्भुज है।
अतः AB \parallel CD एवं AD \parallel BC है।
\angle A+\angle D=180°(क्रमागत अन्त:कोण)……(1)
\angle C+\angle D=180°(क्रमागत अन्त:कोण)……(2)
(1) व (2) से-

\angle A+\angle D=\angle C+\angle D \\ \Rightarrow \angle A=\angle C
इसी प्रकार सिद्ध कर सकते हैं कि \angle B=\angle D
प्रमेय (Theorem):5.एक चतुर्भुज में सम्मुख कोण बराबर हों तो वह समान्तर चतुर्भुज होता है।

दिया है (Given):एक चतुर्भुज ABCD है जिसमें \angle A=\angle C और \angle B=\angle D है।
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
उपपत्ति (Proof):चतुर्भुज ABCD में दिया है
\angle A=\angle C और \angle B=\angle D है।
जोड़ने पर-\angle A+\angle B=\angle C+\angle D……(1)
परन्तु \angle A+\angle B+\angle C+\angle D=360°……(2)
(1) व (2) से-
अर्थात् AB, रेखाओं AD और BC को क्रमशः A और B पर प्रतिच्छेद करती है जिससे
\angle A+\angle B=180°(तिर्यक रेखा के एक ही ओर के अन्त: कोण)
अतः AD \parallel BC…..(3)
इसी प्रकार \angle C+\angle D=180°
अतः AB \parallel DC…..(4)
(3) और (4) से-
ABCD एक समान्तर चतुर्भुज है।
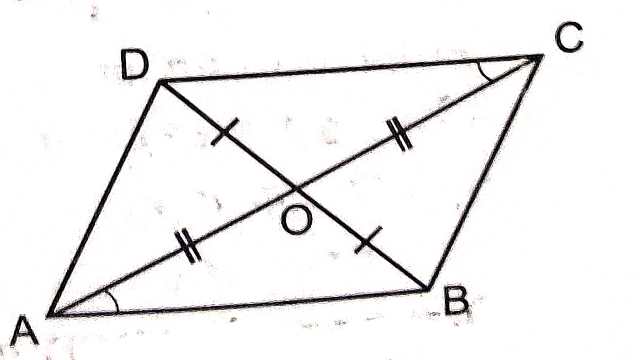
प्रमेय (Theorem):6.समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।

दिया है (Given):एक समान्तर चतुर्भुज के विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove):OA=OC और OB=OD
उपपत्ति (Proof): \triangle AOD एवं \triangle COB में
\angle ADO=\angle OBC (एकान्तर कोण)
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएं)
\angle DAO=\angle OCB(एकान्तर कोण)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Property)

\triangle AOD \cong \triangle COB
अतः सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होंगी।
अर्थात् OD=OB और OA=OC
प्रमेय (Theorem):7.(प्रमेय 6 का विलोम) यदि चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हों तो वह समान्तर चतुर्भुज होता है।

दिया है (Given):एक चतुर्भुज ABCD जिसके विकर्ण AC और BD बिन्दु O पर समद्विभाजित करते हैं अर्थात् OA=OC और OB=OD
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
उपपत्ति (Proof): \triangle AOB और \triangle COD में
OA=OC (दिया है)
\angle AOB= \angle COD(शीर्षाभिमुख कोण)
और OB=OD (दिया है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Property)

\triangle AOB \cong \triangle COD
अतः सर्वांगसम त्रिभुजों के संगत कोण समान होंगे।
अर्थात् \angle OAB= \angle OCD
परन्तु यह तिर्यक रेखा AC द्वारा रेखाओं AB और CD पर बने एकान्तर कोण हैं। अतः

AB \parallel CD
इसी प्रकार AD \parallel BC
अतः ABCD एक समान्तर चतुर्भुज है।
प्रमेय (Theorem):8.एक चतुर्भुज समान्तर चतुर्भुज होता है यदि इसकी सम्मुख भुजाओं का एक युग्म परस्पर बराबर एवं समान्तर हो।

दिया है (Given):एक चतुर्भुज ABCD जिसमें AB \parallel DC और AB=DC है।
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
रचना (Construction):A को C से मिलाया।
उपपत्ति (Proof): AB \parallel DC और तिर्यक रेखा AC इनको प्रतिच्छेद करती है।
अतः \angle BAC= \angle DCA(एकान्तर कोण)…..(1)
अब \triangle ABC और \triangle CDA में
AB=DC (दिया है)
\angle BAC= \angle DCA[(1)से]
AC=AC (उभयनिष्ठ भुजा)
अतः भुजा–कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Property)

\triangle ABC \cong \triangle CDA
अतः सर्वांगसम त्रिभुजों के संगत कोण बराबर होंगे
अर्थात् \angle ACB= \angle CAD

अब AD,BC दो रेखाएं हैं और तिर्यक रेखा AC जिनको इस प्रकार प्रतिच्छेद करती है कि एकान्तर कोण \angle ACB एवं \angle CAD समान हैं।
अतः AD \parallel BC….(2)
अर्थात् AD \parallel BC [( 2)से]
AB \parallel DC(दिया है)
अतः ABCD एक समान्तर चतुर्भुज है।

3.समान्तर चतुर्भुज के गुणधर्म के उदाहरण (Properties of Parallelogram Examples)-

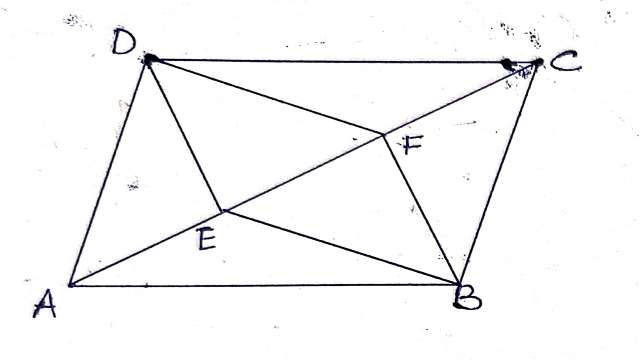
Example-1.समान्तर चतुर्भुज ABCD के विकर्ण AC पर बिन्दु E और F इस प्रकार स्थित हैं कि AE=CF है,दर्शाइए कि BFDE एक समान्तर चतुर्भुज है।

Solution-दिया है (Given):समान्तर चतुर्भुज ABCD के विकर्ण AC पर E व F इस प्रकार स्थित हैं कि AE=CF
सिद्ध करना है (To Prove):BFDE समान्तर चतुर्भुज है।
उपपत्ति (Proof): \triangle ABE तथा \triangle CDF में
AB=CD (समान्तर चतुर्भुज की सम्मुख भुजाएं)
AE=CF(दिया है)
\angle BAE=\angle DCF(एकान्तर कोण)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Property)

\triangle ABE \cong \triangle CDF
BE=DF (सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
\triangle ADE तथा \triangle CBF में
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएं)
\angle DAE=\angle BCF (एकान्तर कोण)
AE=CF (दिया है)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Property)

\triangle ADE \cong \triangle CBF
DE=BF (सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
(1) व (2) से-
BE=DF तथा  DE=BF
अतः BFDE समान्तर चतुर्भुज है।
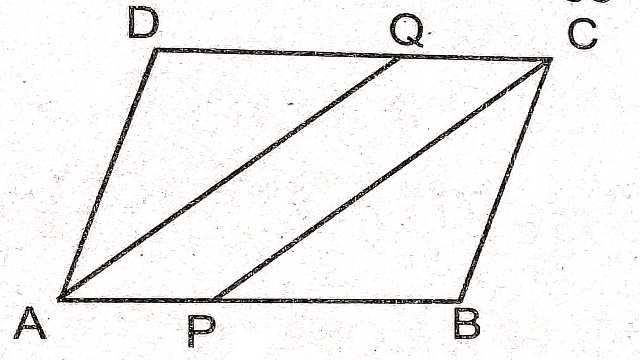
Example-2.चित्र में ABCD एक समान्तर चतुर्भुज है।AQ और CP क्रमशः \angle A और \angle C के समद्विभाजक APCQ एक समान्तर चतुर्भुज है।

Solution-दिया है (Given):ABCD समान्तर चतुर्भुज है तथा AQ व CP क्रमशः \angle A और \angle C के समद्विभाजक हैं।
सिद्ध करना है (To Prove):APCQ एक समान्तर चतुर्भुज है।
उपपत्ति (Proof): \triangle ADQ तथा \triangle CBP  में
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएं)
\angle DAQ= \angle BCP(समान्तर चतुर्भुज के सम्मुख कोण)
\angle D= \angle B(समान्तर चतुर्भुज के सम्मुख कोण)
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Property)

\triangle ADQ \cong \triangle CBP
\angle DQA= \angle BPC(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\angle DQA+\angle CQA=180°(रैखिक कोण युग्म)….(2)
\angle BPC+\angle APC=180°(रैखिक कोण युग्म)……(3)
(2) व (3) से-
\angle DQA+\angle CQA=\angle BPC+\angle APC \\ \Rightarrow  \angle DQA+\angle CQA=\angle DQA+\angle APC [(1) से]

\Rightarrow \angle CQA=\angle APC…..(4)
चतुर्भुज APCQ में
\angle QAP=\angle QCP (समान्तर चतुर्भुज के सम्मुख कोण)
\angle CQA=\angle APC [(4) से]

अतः APCQ समान्तर चतुर्भुज है।
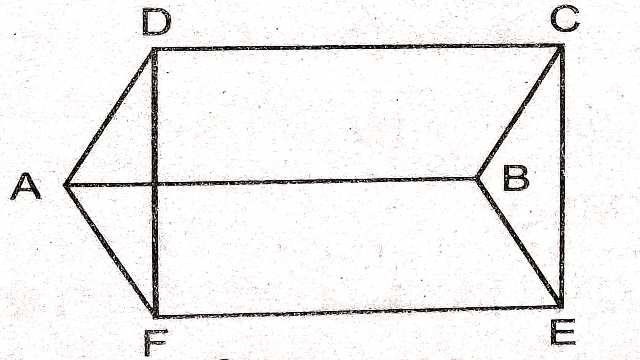
Example-3.चित्र में ABCD और AFEB समान्तर चतुर्भुज है। सिद्ध कीजिए कि CDFE समान्तर चतुर्भुज है।

Solution-दिया है (Given):ABCD व AFEB समान्तर चतुर्भुज है। अर्थात् CD \parallel AB व CD=AB तथा AB \parallel FE व AB=FE
सिद्ध करना है (To Prove):CDFE समान्तर चतुर्भुज है।
उपपत्ति (Proof):CD \parallel AB व CD=AB (दिया है)
AB \parallel FE  व AB=FE (दिया है)
(1) व (2) से-
AB \parallel FE  तथा CD=FE
अतः CDFE समान्तर चतुर्भुज है क्योंकि सम्मुख भुजाओं का एक युग्म समान्तर व बराबर हो तो वह समान्तर चतुर्भुज होता है।
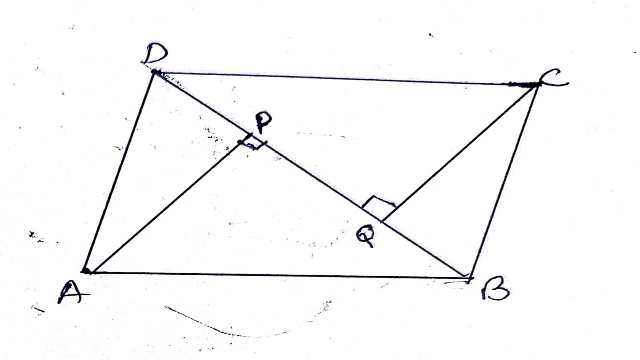
Example-4.ABCD एक समान्तर चतुर्भुज के विकर्ण BD पर A और C से डाले गए लम्ब क्रमशः AP और CQ है। सिद्ध कीजिए कि AP=CQ.

Solution-दिया है (Given):समान्तर चतुर्भुज ABCD में AP \perp BD व  CQ \perp BD
सिद्ध करना है (To Prove):AP=CQ
उपपत्ति (Proof):\triangle ABD \cong \triangle CBD
(सर्वांगसम त्रिभुजों का विकर्ण उसे दो सर्वांगसम त्रिभुजों में बांटता है)

ar(ABD)=ar(CBD) \\ \frac{1}{2} \times BD \times AP=\frac{1}{2} \times BD \times CQ \\ \Rightarrow AP=CQ
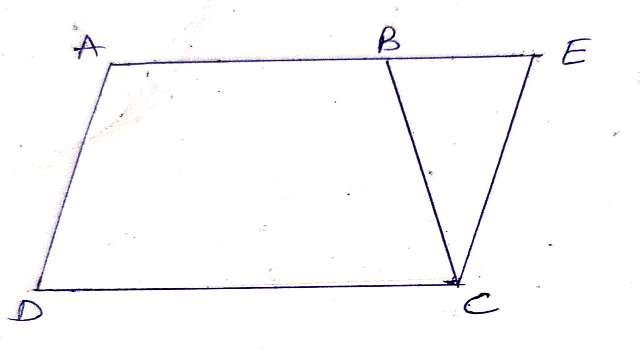
Example-5.चित्र में ABCD एक चतुर्भुज है जिसमें AB \parallel DC और AD=BC हो तो सिद्ध कीजिए कि \angle A=\angle B

Solution-दिया है (Given): चतुर्भुज ABCD में AB \parallel DC और AD=BC
सिद्ध करना है (To Prove):\angle A=\angle B
रचना (Construction):AD \parallel CE खींची तथा BE को मिलाया।

उपपत्ति (Proof):AD=BC (दिया है)
AD \parallel CE (रचना से)
AB \parallel DC (दिया है)
अतः ADCE समान्तर चतुर्भुज है)
AD=CE (समान्तर चतुर्भुज की सम्मुख भुजाएं)
(1) व (2) से-
BC=CE
\angle EBC=\angle BEC (बराबर भुजा के अभिमुख कोण बराबर होते हैं)…..(3)
\angle ABC=\angle BEC+\angle BCE….(4)(त्रिभुज का बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है)
(3)‌ व (4) से-

\angle ABC=\angle EBC+\angle BCE…..(5)
\angle EBC=\angle BCD(एकान्तर कोण)…..(6)
(5) व (6) से-

\angle ABC=\angle BCD+\angle BCE \\ \angle ABC=\angle DCE….(7)
\angle A=\angle DCE(समान्तर चतुर्भुज के सम्मुख कोण)
(7) व (8) से-

\angle A=\angle ABC

अर्थात् \angle A=\angle B
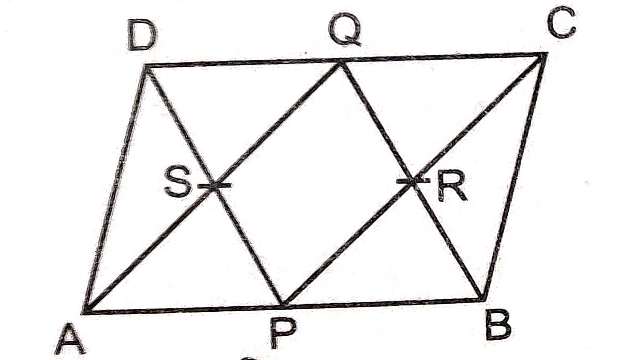
Example-6.चित्र में ABCD एक समान्तर चतुर्भुज है।P और Q क्रमशः सम्मुख भुजाओं ABऔर CD के मध्य सिद्ध कीजिए कि PRQS एक समान्तर चतुर्भुज है।

Solution-दिया है (Given):ABCD एक समान्तर चतुर्भुज है तथा P व Q क्रमशः भुजाओं AB और CD के मध्य बिन्दु है।
सिद्ध करना है (To Prove):PRQS एक समान्तर चतुर्भुज है।
उपपत्ति (Proof):AP \parallel QC तथा AP=QC
अतःAPCQ एक समान्तर चतुर्भुज है।
अतः \angle QAP=\angle QCP(समान्तर चतुर्भुज के सम्मुख कोण)…..(1)
इसी प्रकार DQ \parallel PB तथा DQ=PB
अतः DQBP एक समान्तर चतुर्भुज है।
अतः \angle QDP=\angle QBP (समान्तर चतुर्भुज के सम्मुख कोण)…..(2)
\triangle DPC तथा \triangle BQA में
\angle QAP=\angle QCP[(1) से]
DC=AB (समान्तर चतुर्भुज की सम्मुख भुजाएं)
\angle QDP=\angle QBP [(2)से]
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Property)
\triangle DPC \cong \triangle BQA \\ \angle AQP=\angle DPC (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)…..(3)
\angle DAB=\angle DCB व \angle ADC=\angle ABC (समान्तर चतुर्भुज के सम्मुख कोण)……(4)
(1),(2) व (4) से-
\angle ADP=\angle QBC तथा \angle DAQ=\angle PCB….(5)
\triangle ASD तथा \triangle BRC में
\angle ADP=\angle QBC [(5) से]
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएं)
\angle DAQ=\angle PCB[(5)से]
कोण-भुजा-कोण सर्वांगसमता गुणधर्म से (By ASA Property)

\triangle ASD \cong  \triangle BRC
\angle ASD=\angle BRC (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)…..(6)

\angle ASD=\angle PSQ तथा \angle BRC=\angle PRQ....(7)
(6) व (7) से-

\angle PSQ=\angle PRQ…..(8)
(7) व (8) से-
चतुर्भुज PQRS के सम्मुख कोण बराबर है, अतः PRQS समान्तर चतुर्भुज है।
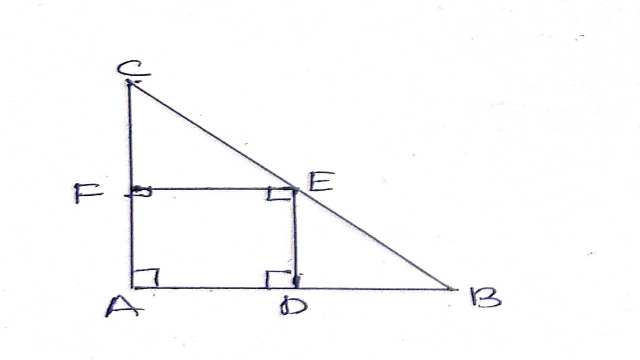
Example-7.कोई वर्ग एक समद्विबाहु समकोण त्रिभुज के अन्तर्गत इस प्रकार है कि वर्ग और त्रिभुज में एक कोण उभयनिष्ठ है।दर्शाइए कि वर्ग का शीर्ष जो उभयनिष्ठ कोण के सम्मुख है कर्ण को समद्विभाजित करता है।

Solution-दिया है (Given):समद्विबाहु \triangle ABC समकोण में वर्ग ADEF का \angle A उभयनिष्ठ है।AB=AC
सिद्ध करना है (To Prove):BE=CE
उपपत्ति (Proof):AB=AC (दिया है)
\angle C=\angle B(बराबर भुजा के अभिमुख कोण बराबर होते हैं)…..(1)
\triangle CFE तथा \triangle BDE में

FE=DE( वर्ग की भुजाएं )
\angle CFE=\angle EDB=90° \\ \angle C=\angle B [(1)से]
भुजा-कोण-कोण सर्वांगसमता गुणधर्म से (By SAS Property)

\triangle CFE \cong \triangle BDE

CE=BE
(सर्वांगसम त्रिभुजों की संगत भुजाएं समान होती है)
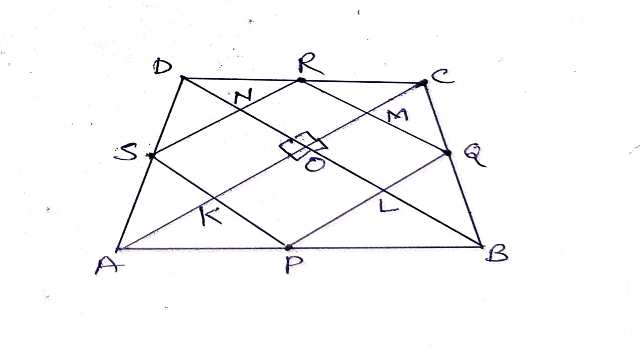
Example-8.P,Q,R और S एक चतुर्भुज ABCD की क्रमशः AB,BC,CD और DA भुजाओं के मध्य-बिन्दु हैं जिसमें AC=BD और AC \perp BD है। सिद्ध कीजिए कि PQRS एक वर्ग है।

Solution-दिया है (Given): चतुर्भुज ABCD में P,Q,R,S क्रमशः AB,BC,CD और DA भुजाओं के मध्य बिन्दु है।AC=BD और AC \perp BD
सिद्ध करना है (To Prove):PQRS एक वर्ग है।
उपपत्ति (Proof):Q,R भुजा BC व DC के मध्य बिन्दु है अतः QR \parallel BD
तथा QR=\frac{1}{2} BD....(1)
इसी प्रकार P,S क्रमशः भुजा AB व AD के मध्य बिन्दु है।
अतः PS \parallel BD तथा PS=\frac{1}{2} BD....(2)
(1) व (2) से-
PQRS एक समान्तर चतुर्भुज है।
परन्तु KONS,PLOK,LQMO,MRNO भी समान्तर चतुर्भुज है। अतः

\angle KSN=\angle KON=90°....(3) \\ \angle KPL=\angle LOK=90°....(4) \\ \angle LQM=\angle LOM=90°....(5) \\ \angle MRN=\angle NOM=90°....(6)
(समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं)
AC=BD तथा QR=PS=\frac{1}{2} BD.....(7)
इसी प्रकार PQ=SR=\frac{1}{2} BD....(8)
(7) व (8) से-

PQ=QR=RS=PS….(9)
(3),(4),(5),(6) व (8) से PQRS वर्ग है।
उपर्युक्त उदाहरणों के द्वारा समान्तर चतुर्भुज के गुणधर्म (Properties of Parallelogram) को समझ सकते हैं।

4.समान्तर चतुर्भुज के गुणधर्म की समस्याएं (Properties of Parallelogram Problems)-

(1.)एक चतुर्भुज के कोण 3:5:9:13 के अनुपात में है।इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
(2.)एक समान्तर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं जो OA=3 cm और OD=2cm है तो AC और BD की लम्बाई ज्ञात कीजिए।
(3.)एक समान्तर चतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।क्या यह कथन सत्य है?अपने उत्तर के लिए कारण दीजीए।
(4.)क्या कोण 110°,80°,70° और 95° किसी चतुर्भुज के कोण हो सकते हैं?क्यों और क्यों नहीं?
(5.)क्या किसी चतुर्भुज के सभी कोण अधिक कोण हो सकते हैं? अपने उत्तर के लिए कारण दीजीए।
(6.)एक चतुर्भुज का एक कोण 108° है तथा अन्य तीनों कोण बराबर है। तीनों कोणों में से प्रत्येक को ज्ञात कीजिए।
उत्तर (Answers):(1.)36°,60°,108°,156°
(2.)AC=6 cm,BD=4 cm
(3.) नहीं,समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
(4.) नहीं, कोणों का योग 360° होना चाहिए।
(5.) नहीं,सभी कोणों का योग 360° से अधिक हो जाएगा जो चतुर्भुज के लिए सम्भव नहीं है।
(6.)84°
उपर्युक्त सवालों को हल करने पर समान्तर चतुर्भुज के गुणधर्मों (Properties of Parallelogram) को ठीक से समझ सकते हैं।

5.समांतर चतुर्भुज के 7 गुण क्या हैं? (What are the 7 properties of a parallelogram?)-

समांतर चतुर्भुज के गुण
सम्मुख भुजाएं सर्वांगसम होती हैं (AB = DC)।
सम्मुख भुजाएं बराबर व समान्तर होती है।
सम्मुख कोण समान होते (D = B) हैं।
आसन्न कोण सम्पूरक हैं (A + D= 180 °)।
यदि एक कोण समकोण है, तो सभी कोण समकोण होंगे।
एक समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
समांतर चतुर्भुज का प्रत्येक विकर्ण इसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।

6.समांतर चतुर्भुज के 4 गुण क्या हैं? (What are the 4 properties of a parallelogram?)-

एक समांतर चतुर्भुज में चार गुण होते हैं:
सम्मुख कोण समान हैं।
सम्मुख भुजाएं समान और समानांतर हैं।
विकर्ण एक दूसरे को समद्विभाजित करते हैं।
किसी भी दो आसन्न कोणों का योग 180° है।

7.सभी समांतर चतुर्भुजों की गुणधर्म क्या है?
What is the property of all parallelograms?),समांतर चतुर्भुज के 6 गुण (6 Properties of Parallelogram)-

यदि एक चतुर्भुज में समानांतर सम्मुख भुजाओं की एक जोड़ी है, तो यह एक विशेष बहुभुज है जिसे पैरेल्लोग्राम कहा जाता है।एक समांतर चतुर्भुज के गुण इस प्रकार हैं:
सम्मुख भुजाएं समानांतर और समान होती हैं
सम्मुख कोण सर्वांगसम हैं
आसन्न कोण सम्पूरक हैं
यदि कोणों में से कोई एक समकोण है, तो अन्य सभी कोण समकोण होंगे
दो विकर्ण एक दूसरे को समद्विभाजित करते हैं।
प्रत्येक विकर्ण समांतर चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है
समांतर चतुर्भुज के सभी भुजाओं के वर्गो का योग इसके विकर्णों के वर्ग के योग के बराबर होता है।इसे समांतर चतुर्भुज नियम भी कहा जाता है।

8.समांतर चतुर्भुज के 8 में से 3 गुण क्या हैं? (What are 3 of 8 properties of a parallelogram?)-

Properties of parallelograms
Opposite sides are congruent (AB = DC).
Opposite angels are congruent (D = B).
Consecutive angles are supplementary (A + D = 180°).
If one angle is right, then all angles are right.
The diagonals of a parallelogram bisect each other.
Each diagonal of a parallelogram separates it into two congruent triangles.

9.समचतुर्भुज के गुण (Properties of Rhombus)-

एक रोम्बस (समचतुर्भुज) के गुण – एक रोम्बस (समचतुर्भुज) एक चतुर्भुज है जिसमें निम्नलिखित चार गुण होते हैं: सम्मुख कोण बराबर होते हैं।सभी भुजाएं समान हैं और, सम्मुख भुजाएं एक दूसरे के समानांतर हैं।विकर्ण एक दूसरे को लंबवत रूप से समद्विभाजित करते हैं।किसी भी दो आसन्न कोणों का योग 180° है।विकर्ण शीर्ष कोण को समद्विभाजित करते हैं।

10.ट्रेपेज़ियम के गुण (Properties of Trapezium)-

एक ट्रेपेज़ियम के गुण।अन्य चतुर्भुजों की तरह, ट्रेपेज़ियम के सभी चार कोणों का योग 360° के बराबर है। एक ट्रेपेज़ियम के दो सम्मुख भुजाएं समानांतर और दो सम्मुख भुजाएं असमानांतर हैं।नियमित ट्रेपेज़ियम के विकर्ण एक दूसरे को समद्विभाजित करते हैं।

11.आयत के गुण (Properties of Rectangular)-

एक आयत एक चतुर्भुज है।सम्मुख भुजाएं समानांतर हैं और एक-दूसरे के बराबर हैं।प्रत्येक आंतरिक कोण 90° डिग्री के बराबर है।एक आयत के विकर्ण एक दूसरे को समद्विभाजित करते हैं।विकर्ण समान अर्थात् सर्वांगसम होते हैं और एक दूसरे को समद्विभाजित करते हैं।

12.पतंग के गुण (Properties of Kite)-

पतंग
दो कोण समान हैं जहां असमान भुजाएं मिलती हैं।
इसे एक सामान्य आधार के साथ सर्वांगसम त्रिभुजों की जोड़ी के रूप में देखा जा सकता है।
इसमें 2 विकर्ण हैं जो एक दूसरे को समकोण पर काटते हैं।
लंबा या मुख्य विकर्ण दूसरे विकर्ण को समद्विभाजित करता है।
एक पतंग अपने मुख्य विकर्ण के बारे में सममित है।

13.समांतर चतुर्भुज का क्षेत्रफल (Area of Parallelogram)-

समांतर चतुर्भुज का क्षेत्रफल ज्ञात करने के लिए,उसकी ऊंचाई अर्थात् लम्ब को आधार से गुणा करें।यह ध्यान दिया जाना चाहिए कि समांतरभुज का आधार इसकी कोई भी भुजा हो सकती है और ऊंचाई जिस भुजा को आधार माना गया है उस पर लम्ब उसकी ऊंचाई लेनी चाहिए।
समान्तर चतुर्भुज के लिए हल क्षेत्रफल=आधार × ऊंचाई (b×h)
उपर्युक्त प्रश्नों के उत्तर, उदाहरणों तथा सवालों को हल करके समान्तर चतुर्भुज के गुणधर्मों (Properties of Parallelogram) को भली-भांति समझ सकते हैं।

Also Read This Article:-Lines and Angles for Class 9

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here