Minima and Maxima in Class 12
1.कक्षा 12 में निम्नतम और उच्चतम (Minima and Maxima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12):
कक्षा 12 में निम्नतम और उच्चतम (Minima and Maxima in Class 12) के इस आर्टिकल की थ्योरी देखने के लिए इससे पूर्व पोस्ट किए गए आर्टिकल को पढ़ना चाहिए।इस आर्टिकल में निम्नतम और उच्चतम को कुछ विशिष्ट ओर उदाहरणों से समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Maxima and Minima in Class 12
2.कक्षा 12 में निम्नतम और उच्चतम के साधित उदाहरण (Minima and Maxima in Class 12 Solved Examples):
Example:10.एक वृत्त और वर्ग के परिमापों का योग k है,जहाँ k एक अचर है।सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है,जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
Solution:माना वर्ग की भुजा x तथा वृत्त की परिधि=2 \pi r
वर्ग तथा वृत्त के परिमापों का योग=4 x+2 \pi r=k \cdots(1) \\ =2 \pi r=k-4 x \\ \Rightarrow r=\left(\frac{k-4 x}{2 \pi}\right) \cdots(2)
वर्ग का क्षेत्रफल=x^2
वृत्त का क्षेत्रफल=\pi r^2
वर्ग तथा वृत्त का क्षेत्रफल का योग A=x^2+\pi r^2 \\ A=x^2+\pi\left(\frac{k-4 x}{2 \pi}\right)^2 [समीकरण (2) से]
\Rightarrow A=x^2+\frac{\pi}{4 \pi^2}\left(k^2-8 k x+16 x^2\right) \\ A=x^2+\frac{1}{4 \pi}\left(k^2-8 k x+16 x^2\right)
x के सापेक्ष अवकलन करने परः
\frac{d A}{d x}=2 x+\frac{1}{4 \pi}(-8 k+32 x) \\ \frac{d A}{d x}=2 x-\frac{2 k}{\pi}+\frac{x}{\pi} \cdots(3)
न्यूनतम के लिए , \frac{d A}{d x}=0 सेः
2 x-\frac{2 k}{\pi}+\frac{8 x}{\pi}=0 \\ \Rightarrow x\left(2+\frac{8}{\pi}\right)=\frac{2 k}{\pi} \\ \Rightarrow x \times 2\left(\frac{\pi+4}{\pi}\right)=\frac{2 k}{\pi} \\ \Rightarrow x=\frac{k}{\pi+4}
समीकरण (3) का पुनः अवकलन करने परः
\frac{d^2 A}{d x^2}=2+\frac{8}{\pi}>0
अतः x=\frac{k}{\pi+4} के लिए क्षेत्रफलों का योग न्यूनतम है।
(2) सेः r=\frac{k-4 x}{2 \pi} \\ \Rightarrow r=\frac{k-4\left(\frac{k}{\pi+4}\right)}{2 \pi} \\ =\frac{k \pi+4 k-4 k}{2 \pi(\pi+4)} \\ =\frac{k \pi}{2 \pi(\pi+4)} \\ r=\frac{k}{2(\pi+4)} \\ \Rightarrow r=\frac{1}{2} x \Rightarrow x=2 r
अतः वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है जबकि दोनों क्षेत्रफलों का योग न्यूनतम है।
Example:11.किसी आयत के ऊपर बने अर्धवृत्त के आकार वाली खिड़की है।खिड़की का सम्पूर्ण परिमाप 10m है।पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लिए खिड़की की विमाएँ ज्ञात कीजिए।
Solution:माना ABCDPA खिड़की है जिसमें APD अर्धवृत्त है।अर्धवृत्त का केन्द्र O है।
AD=2r,AB=x=CD
अर्धवृत्त की परिधि=\pi r
खिड़की का परिमाप=2 x+2 r+\pi r=10 मीटर ……(1)
r(\pi+2)=10-2 x \\ r=\frac{10-2 x}{\pi+2}
खिड़की का क्षेत्रफल A=\frac{1}{2} \pi r^2+2 r x \\ A=\frac{\pi}{2}\left(\frac{10-2 x}{\pi+2}\right)^2+ 2\left(\frac{10-2 x}{\pi+2}\right) x [समीकरण (2) से]
A=\frac{\pi}{2(\pi+2)^{2}}\left(100-40 x+4 x^2\right)+\frac{2}{\pi+2}\left(10 x-2 x^2\right) \\ =\frac{1}{2(\pi+2)^2}(100 \pi-40 \pi x+4 \pi x^2+40 \pi x-8 \pi x^2+80x-16 x^{2}) \\ =\frac{1}{2(\pi+2)^2}\left(140 \pi-41 x^2+80 x-16 x^2\right)
x के सापेक्ष अवकलन करने परः
\frac{d A}{d x}=\frac{1}{2(\pi+2)^2}(-8 \pi x+80-32 x) \cdots(3)
A अधिकतम होगा यदि , \frac{d A}{d x}=0 \\ -8 \pi x+80-32 x=0 \\ 8 x(\pi+4)=80 \\ \Rightarrow x=\frac{10}{\pi+4}
समीकरण (3) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 A}{d x^2} =\frac{1}{2(\pi+2)^2}(-8 \pi-32) \\ =\frac{-8(\pi+4)}{2(\pi+2)^2} \\ \Rightarrow \frac{d^2 A}{d x^2} =\frac{-4(\pi+4)}{(\pi+2)^2}<0
अब x=\frac{10}{\pi+4} पर क्षेत्रफल अधिकतम होगा।
x का मान समीकरण (2) में रखने परः
r=\frac{10-2 \times \frac{10}{(\pi+4)}}{(\pi+2)} \\ =\frac{10 \pi+40-20}{(\pi+2)(\pi+4)} \\ =\frac{10 \pi+20}{(\pi+2)(\pi+4)} \\ =\frac{10(\pi+2)}{(\pi+2)(\pi+4)} \\ r=\frac{10}{\pi+4} तथा x=\frac{10}{\pi+4}
लम्बाई=\frac{20}{\pi+4}, चौड़ाई=\frac{10}{\pi+4}
Example:12.त्रिभुज की भुजाओं से a और b दूरी पर त्रिभुज के कर्ण पर स्थित एक बिन्दु है।सिद्ध कीजिए कि कर्ण की न्यूनतम लम्बाई \left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}} है।
Solution:माना \triangle ABC एक समकोण त्रिभुज है जिसमें \angle B=90^{\circ} तथा कर्ण AC पर बिन्दु P है जो कि भुजा AB से a दूरी पर तथा भुजा BC से b दूरी पर है।
PM भुजा AB पर लम्ब है तथा PN भुजा BC पर लम्ब है।पुनः माना \angle ACB=\theta=\angle APM \\ \triangle AMP में \sec \theta= \frac{\text{कर्ण}}{\text{आधार}} \\ \frac{A P}{a} \Rightarrow A P=a \sec \theta \\ \triangle PNC में cosec \theta= \frac{\text{कर्ण}}{\text{लम्ब}} \\ cosec \theta=\frac{P C}{b} \\ bc=b \operatorname{cosec} \theta
अतः कर्ण AC=AP+PC
L=a \sec \theta+b \operatorname{cosec} \theta \cdots(1) \\ \theta के सापेक्ष अवकलन करने परः
\frac{d L}{d \theta}=a \sec \theta \tan \theta-b \operatorname{cosec} \theta \cot \theta \cdots(2)
न्यूनतम के लिए \frac{d L}{d \theta}=0 \\ a \sec \theta \tan \theta - b \operatorname{cosec} \theta \cot \theta=0 \\ \Rightarrow \frac{a}{\cos \theta} \cdot \frac{1}{\sin \theta}=b \cdot \frac{1}{\sin \theta} \cdot \frac{\cos \theta}{\sin \theta} \\ \Rightarrow \frac{\sin ^3 \theta}{\cos ^3 \theta}=\frac{b}{a} \Rightarrow \tan ^3 \theta=\frac{b}{a} \\ \Rightarrow \tan \theta=\frac{b^{\frac{1}{3}}}{a^{\frac{1}{3}}}
कर्ण=\sqrt{\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)}
समीकरण (2) का पुनः \theta के सापेक्ष अवकलन करने परः
\frac{d^2 L}{d \theta^2}= a \sec \theta \tan ^2 \theta+a \sec ^3 \theta+b \operatorname{cosec}^2 \theta \cot ^2 \theta +b \operatorname{cosec}^3 \theta \\ = a \cdot \frac{\sqrt{\left(b^{\frac{2}{3}}+ a^{\frac{2}{3}}\right)}}{a^{\frac{1}{3}}} \cdot \frac{b^{\frac{2}{3}}}{a^{\frac{2}{3}}}+a \cdot \frac{\left( b^{\frac{2}{3}}+ a^{\frac{2}{3}}\right)^{\frac{3}{2}}}{a}+b \frac{\sqrt{\left(b^{\frac{2}{3}} + a^{\frac{2}{3}} \right)}}{b^{\frac{1}{3}}} \cdot \frac{a^{\frac{2}{3}}}{b^{\frac{2}{3}}}+b \frac{\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)^{\frac{3}{2}}}{b} \\ = b^{\frac{2}{3}} \sqrt{\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)} +\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)^{\frac{3}{2}}+a^{\frac{2}{3}} \sqrt{\left(b^{\frac{2}{3}}+ a^{\frac{2}{3}}\right)}+\left(a^{\frac{2}{3}}+a^{\frac{2}{3}}\right)^{\frac{3}{2}} \\ =\sqrt{\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)}\left[b^{\frac{2}{3}}+b^{\frac{2}{3}}+a^{\frac{2}{3}}+a^{\frac{2}{3}}+a^{\frac{2}{3}}+b^{\frac{2}{3}}\right] \\= 3 \sqrt{\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)} \left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right) \\ \Rightarrow \frac{d^2 L}{d \theta^2} =3\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}>0
अतः \tan \theta=\frac{b^{\frac{1}{3}}}{a^{\frac{1}{3}}} पर कर्ण की लम्बाई न्यूनतम होगी।
कर्ण की लम्बाई L=a \sec \theta+b \operatorname{cosec} \theta \\ =a \times \frac{\sqrt{ \left( a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)}}{a^{\frac{1}{3}}}+b \times \frac{ \sqrt{\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)}}{b^{\frac{1}{3}}} \\ =a^{\frac{2}{3}} \sqrt{\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)}+b^{\frac{2}{3}} \sqrt{\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)} \\ =\sqrt{\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right) \left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)} \\ L=\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}
Example:13.उन बिन्दुओं को ज्ञात कीजिए जिन पर f(x)=(x-2)^4(x+1)^3 द्वारा प्रदत्त फलन f का,
(i) स्थानीय उच्चतम बिन्दु है (ii) स्थानीय निम्नतम बिन्दु है (iii) नति परिवर्तन बिन्दु है।
Solution: f(x)=(x-2)^4(x+1)^3
x के सापेक्ष अवकलन करने परः
f^{\prime}(x) =4(x-2)^3(x+1)^3+(x-2)^4 \cdot 3(x+1)^2 \\ =(x-2)^3(x+1)^2(4 x+4+3 x-6) \\ \Rightarrow f^{\prime}(x)=(x-2)^3(x+1)^2(7 x-2)
स्थानीय उच्चतम/निम्नतम के लिए f'(x)=0 सेः
(x-2)^3(x+1)^2(7 x-2)=0 \\ \Rightarrow x=-1, \frac{2}{7}, 2
(i) x=-1 के लिए
x=-1.1 लेने पर (-1 के बायीं ओर)
f(-1.1) =(-1.1-2)^3(-1.1+1)^2[7(-1.1)-2] \\ =(-3.1)^3(-0.1)^2(-9.7) \\ \Rightarrow f^{\prime}(-1.1) =2.889727>0
अब x=-0.9 लेने पर (-1 के दायीं ओर)
f^{\prime}(-0.9) =(-0.9-2)^3(-0.9+1)^2[7(-0.9)-2] \\ =(-2.9)^3(0.1)^2(-8.3) \\ \Rightarrow f(-0.9) =2.024287>0
अतः x=-1 पर फलन का चिन्ह परिवर्तित नहीं होता है।
x=-1 नति परिवर्तन बिन्दु है।
(ii) x=\left(\frac{2}{7}\right) के लिए
x=\left(\frac{1}{7}\right) लेने पर ( \left(\frac{2}{7}\right) के बायीं ओर)
f^{\prime}\left(\frac{1}{7}\right) =\left(\frac{1}{7}-2\right)^3\left(\frac{1}{7}+1\right)^2\left(7 \times \frac{1}{7}-2\right) \\ =\left(-\frac{13}{7}\right)^3\left(\frac{8}{7}\right)^2(-1) \\ \Rightarrow f^{\prime}\left(\frac{1}{7}\right) =\frac{140608}{16807}>0 \\ x=\left(\frac{3}{7}\right) को लेने पर (x=\left(\frac{2}{7}\right) के दायीं ओर)
f^{\prime}\left(\frac{3}{7}\right) =\left(\frac{3}{7}-2\right)^3\left(\frac{3}{7}+1\right)^2\left(7 \times \frac{3}{7}-2\right) \\ =\left(-\frac{11}{7}\right)^3\left(\frac{10}{7}\right)^2(1) \\ f^{\prime}\left(\frac{3}{7}\right) =-\frac{133100}{16807}<0 \\ \Rightarrow f'(x) का चिन्ह धनात्मक से ऋणात्मक में परिवर्तित होता है।अतः x=\left(\frac{2}{7}\right) फलन का स्थानीय उच्चतम बिन्दु है।
(iii) x=2 के लिए
x=1.9 लेने पर (2 के बायीं ओर)
f^{\prime}(1.9)=(1.9-2)^3(1.9+1)^2(7 \times 1.9-2) \\ =(-0.1)^3(2.9)^2(11.3) \\ \Rightarrow f^{\prime}(1.9)=-0.095033<0
x=2.1 लेने पर (2 के दायीं ओर)
f^{\prime}(2.1)=(2.1-2)^3(2.1+1)^2(7 \times 2.1-2) \\ \Rightarrow f^{\prime}(2.1)=(0.1)^3(3.1)^2(12.7) \\ \Rightarrow f^{\prime}(2.1)=0.122047>0
अतः x=2 पर f'(x) का चिन्ह ऋणात्मक से धनात्मक में परिवर्तित होता है।
x=2 फलन का स्थानीय निम्नतम बिन्दु है।
उत्तर (i) x=\frac{2}{7} फलन का स्थानीय उच्चतम बिन्दु है
(ii) x=2 फलन का स्थानीय निम्नतम बिन्दु है
(iii) x=-1 फलन का नति परिवर्तन बिन्दु है।
Example:14. f(x)=\cos ^2 x+\sin x, x \in[0, \pi] द्वारा प्रदत्त फलन f का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।
Solution: f(x)=\cos ^2 x+\sin x
x के सापेक्ष अवकलन करने परः
f^{\prime}(x)=-2 \sin x \cos x+\cos x \\ \Rightarrow f^{\prime}(x)=\cos x(-2 \sin x+1)
उच्चतम/निम्नतम के लिए f'(x)=0
f'(x)=0 सेः
\cos x(-2 \sin x+1)=0 \\ \Rightarrow \cos x=0,-2 \sin x+1=0 \Rightarrow \sin x=\frac{1}{2} \\ \Rightarrow \cos x=\cos \frac{\pi}{2} , \sin x=\sin \frac{\pi}{6} \\ \Rightarrow x=\frac{\pi}{6}, \frac{\pi}{2} \\ \frac{\pi}{6}, \frac{\pi}{2} \in[0, \pi] \\ f(0)=\cos ^2 0+\sin 0=1+0=1 \\ f(\frac{\pi}{6})=\cos ^2 \frac{\pi}{6}+\sin \frac{\pi}{6}=\left(\frac{\sqrt{3}}{2}\right)^2+\frac{1}{2} \\ \Rightarrow f(\frac{\pi}{6})=\frac{3}{4}+\frac{1}{2}=\frac{5}{4} \\ f(\frac{\pi}{2})=\cos ^2 \frac{\pi}{2}+\sin \frac{\pi}{2} \\ =0+1 \\ \Rightarrow f\left(\frac{\pi}{2}\right)=1
अतः निरपेक्ष उच्चतम मान=\frac{5}{4}
निरपेक्ष निम्नतम मान=1
Example:15.सिद्ध कीजिए कि एक r त्रिज्या के गोले के अन्तर्गत उच्चतम आयतन के लम्ब वृत्तीय शंकु की ऊँचाई \frac{4r}{3} है।
Solution:माना ABC शंकु है जो कि r त्रिज्या के गोले के अन्तर्गत बना है।गोले का केन्द्र O है।
माना शंकु की त्रिज्या=R
शंकु की ऊँचाई (h)=AM=AP-MP
AM=(2r-x) (MP=x)
समकोण \triangle OMB में
OM^2+B M^2=O B^2 \\ \Rightarrow (r-x)^2+R^2=r^2 \\ \Rightarrow R^2=r^2-(r-x)^2 \\ \Rightarrow R^2=r^2-\left(r^2-2 r x+x^2\right) \\ \Rightarrow R^2=r^2-r^2+2 r x-x^2 \\ \Rightarrow R^2=2 r x-x^2
शंकु का आयतन v=\frac{1}{3} \pi R^2 h \\ \Rightarrow v=\frac{1}{3} \pi\left(2 r x-x^2\right) \times(2 r-x) \\ v=\frac{1}{3} \pi\left(4 r^2 x-4 r^2+x^3\right)
x के सापेक्ष अवकलन करने परः
dv=\frac{1}{d x} \pi\left(4 r^2-8 r x+3 x^2\right) \cdots(1) \\ =\frac{1}{3} \pi\left[4 r^2-6 r x-2 r x+3 x\right] \\ =\frac{1}{3} \pi[2 r(2 r-3 x)-x(2 r-3 x)] \\ \Rightarrow \frac{d v}{d x} =\frac{1}{3} \pi[(2 r-x)(2 r-3 x)]
महत्तम के लिए \frac{d V}{d x}=0 सेः
\frac{4}{3} \pi(2 r-x)(2 r-3 x)=0 \\ \Rightarrow x=2 r, \frac{2}{3} r \\ x=2 r (असंभव है)
पुनः समीकरण (1) का x के सापेक्ष अवकलन करने परः
\frac{d^2 v}{d x^2}=\frac{1}{3} \pi(-8 r+6 x) \\ \left(\frac{d^2 v}{d x^2}\right)_{\left(x=\frac{2}{3} r\right)}=\frac{1}{3} \pi\left(-8 r+6 \times \frac{2}{3} r\right) \\ =\frac{1}{3} \pi(-4 r) \\ \Rightarrow \left(\frac{d^2 v}{d x^2}\right)_{\left(x=\frac{2 r}{3}\right)}=-\frac{4 \pi r}{3}<0
अतः x=\frac{2}{3} r के लिए आयतन महत्तम होगा।
शंकु की ऊँचाई h=AM=2r-x \\ h=2 r-\frac{2 r}{3} \\ \Rightarrow h=\frac{4 r}{3}
Example:16.मान लीजिए [a,b] पर परिभाषित एक फलन f है इस प्रकार कि सभी x \in(a, b) के लिए f'(x)>0 है तो सिद्ध कीजिए कि (a,b) पर एक वर्धमान फलन है।
Solution:माना x_1, x_2 \in \left(a, b\right) इस प्रकार है कि के लिए f(x) अन्तराल (a,b) में अवकलनीय है तथा
\left[x_1, x_2\right] \in(a, b) फलन f अन्तराल \left[x_1, x_2\right] पर सतत है और \left(x_1, x_2\right) में अवकलनीय है।तब मध्यमान प्रमेय सेः
\therefore c \in\left(x_1, x_2\right) का अस्तित्व इस प्रकार है कि
f^{\prime}(c)=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1} \cdots(1)
यहाँ (a,b) के लिए f'(x)>0
f'(c)>0 \left[\because c \in \left(x_1, x_2\right), c \in (a, b)\right] \\ \Rightarrow c \in(a, b)
तथा f^{\prime}(c)>0 \Rightarrow \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0 \\ \Rightarrow f\left(x_2\right)-f\left(x_1\right)>0 \left(\because x_2-x_1>0 \text{ जब } x_1<x_2\right) \\ \Rightarrow f\left(x_2\right)>f\left(x_1\right) \\ \Rightarrow f\left(x_1\right)<f\left(x_2\right) \text { यदि } x_1<x_2
क्योंकि x_1, x_2 \in(a, b) स्वेच्छ बिन्दु है।
\therefore x_1<x_2 \Rightarrow f\left(x_1\right)<f\left(x_2\right) \forall x_1, x_2 \in(a, b) \\ \therefore f(x) अन्तराल (a,b) में वर्धमान है।
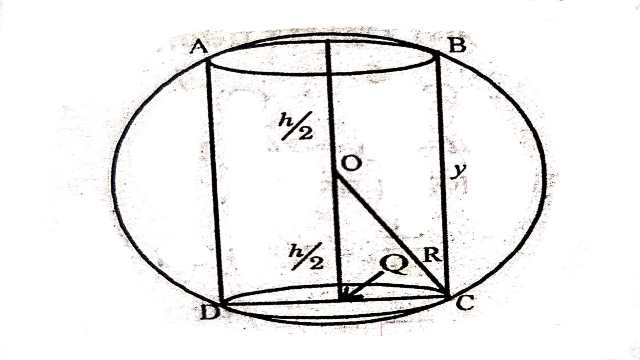
Example:17.सिद्ध कीजिए कि एक r त्रिज्या के गोले के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई \frac{2R}{\sqrt{3}} है।अधिकतम आयतन भी ज्ञात कीजिए।
Solution:माना ABCD बेलन है जो R त्रिज्या के गोले के अन्तर्गत बना है।गोले का केन्द्र O है।
माना h तथा r क्रमशः बेलन की ऊँचाई व त्रिज्या है तथा बेलन का आयतन V
V=\pi r^2 h \ldots(1)
समकोण \triangle OQC में
R^2=O Q^2+Q C^2 \\ =\left(\frac{h}{2}\right)^2+r^2 \\ \Rightarrow r^2=R^2-\frac{h^2}{4} \\ \therefore V=\pi\left(R^2-\frac{h^2}{4}\right) \times h [(1) से]
V=\pi\left(R^2 h-\frac{h^3}{4}\right)
h के सापेक्ष अवकलन करने परः
\frac{d V}{d h}=\pi R^2-\frac{3}{4} \pi h^2 \ldots(2)
उच्चतम आयतन के लिए \frac{dV}{dh}=0 सेः
\pi R^2-\frac{3}{4} \pi h^2=0 \\ \Rightarrow \frac{3}{4} h^2=R^2 \Rightarrow h=\frac{2 R}{\sqrt{3}}
समीकरण (2) का पुनः h के सापेक्ष अवकलन करने परः
\frac{d^2 V}{d h^2}=-\frac{3}{2} \pi h \\ \left(\frac{d^2 V}{d h^2}\right)_{\left(h=\frac{2 R}{\sqrt{3}} \right)}=-\frac{3}{2} \pi \times \frac{2 R}{\sqrt{3}}=-\sqrt{3} \pi R<0
अतः h=\frac{2 R}{\sqrt{3}} पर बेलन का आयतन महत्तम होगा।
बेलन का आयतन=\pi\left[R^2-\frac{1}{4} \times \frac{4 R^2}{3}\right] \times \frac{2 R}{\sqrt{3}} \\ =\pi\left[\frac{2 R^2}{3}\right] \times \frac{2 R}{\sqrt{3}} \\ V=\frac{4 \pi R^3}{3 \sqrt{3}}, \quad h=\frac{2 R}{\sqrt{3}}
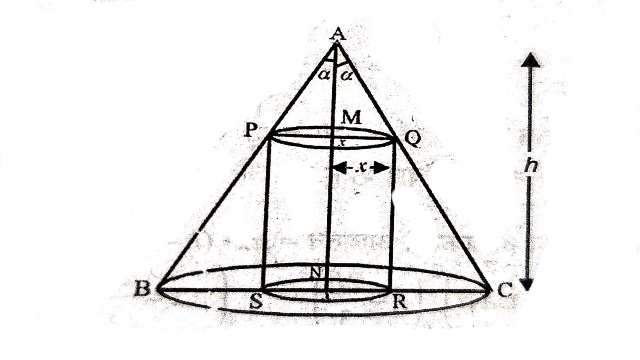
Example:18.सिद्ध कीजिए कि अर्धशीर्ष कोण \alpha और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई,शंकु के ऊँचाई की एक तिहाई है और बेलन का अधिकतम आयतन \frac{4}{27} \pi h^3 \tan ^2 \alpha है।
Solution:माना ABC शंकु है।शंकु की ऊँचाई=h
अर्धशीर्ष कोण=\alpha
PQRS बेलन शंकु ABC के अन्तर्गत बनाया गया है।
माना बेलन की त्रिज्या x है।
बेलन की ऊँचाई=MN=AN-AM=h-x \cot \alpha \\ \because \triangle AMQ में \cot \alpha=\frac{A M}{x}
बेलन का आयतन V=\pi x^2(h-x \cot \alpha)
x के सापेक्ष अवकलन करने परः
\frac{d V}{d x}=2 \pi r(h-x \cot \alpha)+\pi x^2(-1 \cdot \cot \alpha) \\ \Rightarrow \frac{d v}{d x}=2 \pi x h-2 \pi x^2 \cot \alpha-\pi x^2 \cot \alpha \\ \Rightarrow \frac{d v}{d x}=2 \pi x h-3 \pi x^2 \cot \alpha \cdots(1)
बेलन का अधिकतम आयतन होगा यदि \frac{dV}{dx}=0
अतः 2 \pi x h-3 \pi x^2 \cot \alpha=0 \\ \Rightarrow x=\frac{2 h}{3 \cot \alpha}
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 V}{d x^2}=2 \pi h-6 \pi x \cot \alpha \\ \left(\frac{d^2 V}{d x^2}\right)_{\left(x-\frac{2 h}{3 \cot \alpha}\right)}=2 \pi h-6 \pi \times \frac{2 h}{3 \cot \alpha} \cdot \cot \alpha \\ =2 \pi h-4 \pi h \\ \Rightarrow \left(\frac{d^{2} v}{d x^2}\right)_{\left(x=\frac{2 h}{3 \cot \alpha}\right)}=-2 \pi h<0
अतः आयतन V अधिकतम है जब x=\frac{2 h}{3 \cot \alpha} \\ x=\frac{2}{3} h \tan \alpha
बेलन की ऊँचाई=h-x \cot \alpha \\ =h-\frac{2}{3} h \tan \alpha \cot \alpha \\ =\frac{1}{3} h
बेलन की ऊँचाई =\frac{1}{3} \times (शंकु की ऊँचाई)
अतः बेलन की ऊँचाई शंकु की ऊँचाई की एक तिहाई है।
बेलन का आयतन V=\pi x^2(h-x \cot \alpha) \\ =\pi\left(\frac{2 h}{3} \tan \alpha\right)^2 \times \frac{1}{3} h \\ \Rightarrow V=\frac{4}{27} \pi h^3 \tan ^2 \alpha
19 से 24 तक के प्रश्नों के सही उत्तर चुनिए।
Example:19.एक 10m त्रिज्या के बेलनाकार टंकी में 314 घनमीटर प्रति घंटा की दर से गेहूँ भरा जाता है।भरे गए गेहूँ की गहराई की वृद्धि दर हैः
(A)1m/h (B)0.1m/h (C)1.1m/h (D)0.5m/h
Solution:बेलनाकार टंकी का आयतन V=\pi r^{2}h
t के सापेक्ष अवकलन करने परः
\frac{d V}{d t}=\pi r^2 \frac{d H}{d t} \\ \frac{d v}{d t}=314 \mathrm{~m}^3 / \mathrm{h} तथा r=10m रखने परः
314=3.14 \times\left(10\right)^2 \times \frac{d h}{d t} \\ \Rightarrow \frac{d h}{d t}=1
अतः विकल्प (A) सही है।
Example:20.वक्र x=t^2+3 z-8, y=2 t^2-2 t-5 के बिन्दु (2,-1) पर स्पर्श रेखा की प्रवणता हैः
(A)\frac{22}{7} (B)\frac{6}{7} (C)\frac{7}{6} (D)-\frac{6}{7}
Solution: x=t^2+3 z-8, y=2 t^2-2 t-5
t के सापेक्ष अवकलन करने परः
\frac{d x}{d t}=2 t+3, \quad \frac{d y}{d t}=4 t-2 \\ \frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{4 t-2}{2 t+3} \ldots(1) \\ \Rightarrow x=t^2+3 t-8 में x=2 रखने परः
2=t^2+3 t-8 \Rightarrow t^2+3 t-10=0 \\ \Rightarrow t^2+5 t-2 t-10=0 \\ \Rightarrow t(t+5)-2(t+5)=0 \\ \Rightarrow(t-2)(t+5)=0 \\ \Rightarrow t=2,-5 \\ y=2 t^2-2 t-5 में y=-1 रखने परः
-1=2 t^2-2 t-5 \\ \Rightarrow 2 t^2-2 t-4=0 \\ \Rightarrow t^2-t-2=0 \\ \Rightarrow t^2-2 t+t-2=0 \\ \Rightarrow t(t-2)+1(t-2)=0 \\ \Rightarrow(t+1)(t-2)=0 \\ \Rightarrow t=-1,2
दोनों में t=2 उभयनिष्ठ है।
\therefore t=2 पर \frac{d y}{d x}=\frac{4 \times 2-2}{2 \times 2+3}=\frac{6}{7}
स्पर्श रेखा की प्रवणता=\frac{6}{7}
अतः विकल्प (B) सही है।
Example:21.रेखा y=mx+1,वक्र y^2=4 x की एक स्पर्श रेखा है यदि m का मान हैः
(A)1 (B)2 (C) 3 (D)\frac{1}{2}
Solution: y^2=4 x \ldots(1)
x के सापेक्ष अवकलन करने परः
2 y \frac{d y}{d x}=4 \Rightarrow \frac{d y}{d x}=m=\frac{2}{y} \ldots(2) \\ y^2=4 x में y=mx+c से x=\frac{y-1}{m}=\frac{(y-1) y}{2} y रखने परः
y^2=\frac{4 y(y-1)}{2} \Rightarrow y=2 y-2 \Rightarrow y=2
अतः \frac{d y}{d x}=m=\frac{2}{2}=1
अतः विकल्प (A) सही है।
Example:22.वक्र 2 y+x^2=3 के बिन्दु (1,1) पर अभिलम्ब का समीकरण हैः
(A)x+y=0 (B)x-y=0 (C)x+y+1=0 (D)x-y=0
Solution: 2 y+x^2=3
x के सापेक्ष अवकलन करने परः
2 \frac{d y}{d x}+2 x=0 \\ \frac{d y}{d x}=\frac{-2 x}{2} \Rightarrow \frac{d y}{d x}=-x \\ \Rightarrow \left(\frac{d y}{d x}\right)_{(1,1)}=-1
अभिलम्ब का समीकरण
\left(y-y_0\right) \frac{d y}{d x}+\left(x-x_0\right)=0 \\ \Rightarrow(y-1)(y)+(x-1)=0 \\ \Rightarrow-x+y=0 \Rightarrow x-y=0
अतः विकल्प (B) सही है।
Example:23.वक्र x^2=4 y का बिन्दु (1,2) से होकर जाने वाला अभिलम्ब हैः
(A)x+y=3 (B)x-y=3 (C)x+y=1 (D)x-y=1
Solution: x^2=4 y \cdots(1)
x के सापेक्ष अवकलन करने परः
2 x=4 \frac{d y}{d x} \Rightarrow \frac{d y}{d x}=\frac{x}{2} \\ \Rightarrow \left(\frac{d y}{d x}\right)_{(1,2)}=\frac{1}{2}
अभिलम्ब का समीकरणः (y-y_{0}) \frac{d y}{d x}+\left(x-x_0\right)=0 \\ \Rightarrow(y-2) \frac{1}{2}+(x-1)=0 \Rightarrow 2 x+y-4=0
प्रश्न में 2x+y-4=0 का कोई विकल्प नहीं दिया गया है।
Example:24.पर वे बिन्दु जहाँ पर वक्र का अभिलम्ब अक्षों से समान अन्तःखण्ड बनाता हैः
(A) \left(4, \pm \frac{8}{3}\right) (B)\left(4,-\frac{8}{3}\right) (C)\left(4, \pm \frac{3}{8}\right) (D) \left(\pm 4, \frac{3}{8}\right)
Solution: 9 y^2=x^3 \ldots(1)
x के सापेक्ष अवकलन करने परः
18 y \frac{d y}{d x}=3 x^2 \Rightarrow \frac{d y}{d x}=\frac{x^2}{6 y}
अभिलम्ब की प्रवणता=-\frac{1}{\frac{d y}{d x}}=-\frac{6 y}{x^2} \ldots(2)
अभिलम्ब अक्षों से समान अन्तःखण्ड बनाता है अतः
अभिलम्ब की प्रवणता
\frac{1}{-\frac{d y}{d x}}=\pm 1 \\ \frac{-6 y}{x^{2}}=\pm 1 \Rightarrow y=\pm \frac{x^2}{6}
y का मान समीकरण (1) में रखने परः
x का मान समीकरण (1) में रखने परः
y^2=\frac{64}{9} \Rightarrow y=+\frac{8}{3}
अतः बिन्दु \left(4, \pm \frac{8}{3}\right) है।
फलतः सही विकल्प (A) है।
उपर्युक्त उदाहरणों के द्वारा कक्षा 12 में निम्नतम और उच्चतम (Minima and Maxima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) को समझ सकते हैं।
3.कक्षा 12 में निम्नतम और उच्चतम के सवाल (Minima and Maxima in Class 12 Questions):
(1.)एक दीर्घवृत्त के \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 किसी बिन्दु P पर अभिलम्ब खींचा गया है सिद्ध कीजिए कि दीर्घवृत्त के केन्द्र से अभिलम्ब की अधिकतम दूरी a-b है।
(2.)धातु की एक आयताकार चादर के कोनों से चार समान वर्ग काट लिए गए हैं।भुजाओं को ऊपर की ओर मोड़कर एक खुला आयताकार सन्दूक बनाया गया है।सिद्ध कीजिए कि सन्दूक का आयतन महत्तम होगा जबकि सन्दूक की गहराई \frac{1}{6}\left[(a+b)-(a^{2}+ab+b^{2})\right] है, जहाँ a,b मूल आयत की भुजाएँ हैं।
उपर्युक्त सवालों को हल करने पर कक्षा 12 में निम्नतम और उच्चतम (Minima and Maxima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) को ठीक से समझ सकते हैं।
Also Read This Article:-Tangents and Normals in Class 12
4.कक्षा 12 में निम्नतम और उच्चतम (Frequently Asked Questions Related to Minima and Maxima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सापेक्ष उच्चिष्ठ एवं निम्निष्ठ मान की परिभाषा दीजिए। (Define Relative Maximum and Minimum Value):
उत्तर:फलन f(x) का मान x=c पर सापेक्ष उच्चिष्ठ कहलाता है यदि फलन f(x) का मान x=c के अल्प प्रतिवेश के प्रत्येक बिन्दु पर f(c) छोटा है अर्थात्
f(x) \leq f(c) \forall x \in(c-h, c+h)
जहाँ h एक धनात्मक अल्पराशि है।
इसी प्रकार फलन f(x) का मान बिन्दु x=c पर सापेक्ष निम्निष्ठ कहलाता है यदि फलन f(x) का मान x=c के अल्प प्रतिवेश के प्रत्येक बिन्दु पर f(c) से बड़ा है अर्थात्
f(x) \geq f(c) \forall x \in(c-h, c+h)
सापेक्ष उच्चिष्ठ को सामान्यतः उच्चिष्ठ या अधिकतम तथा सापेक्ष निम्निष्ठ मान को सामान्यतः निम्निष्ठ या न्यूनतम मान कहते हैं।
प्रश्न:2.निरपेक्ष उच्चिष्ठ एवं निम्निष्ठ मान की परिभाषा दीजिए। (Define Absolute Maximum and Minimum):
उत्तरःफलन f(x) का मान प्रान्त D में बिन्दु x=c पर निरपेक्ष उच्चिष्ठ या निरपेक्ष अधिकतम (greatest) कहलाता है यदि
f(x) \leq f(c) ; \forall x \in D
तथा फलन f(x) का मान प्रान्त D में बिन्दु x=c पर निरपेक्ष निम्निष्ठ या निरपेक्ष न्यूनतम (Least) कहलाता है यदि
f(x) \geq f(c) ; \forall x \in D
टिप्पणीःकिसी प्रान्त में फलन के उच्चिष्ठ एवं निम्निष्ठ मान एक से अधिक हो सकते हैं परन्तु प्रान्त में निरपेक्ष अधिकतम या निरपेक्ष न्यूनतम मान केवल एक ही होता है।एक उच्चिष्ठ मान,निम्निष्ठ मान से कम हो सकता है इसी प्रकार एक निम्निष्ठ मान,उच्चिष्ठ मान से अधिक हो सकता है।फलन के उच्चिष्ठ एवं निम्निष्ठ मान को चरम मान कहते हैं।
प्रश्न:3.स्तब्ध बिन्दु और चरम बिन्दु में क्या अन्तर है? (What is the Difference Between Stationary Point and Extreme Point?):
उत्तरःवे बिन्दु जिन पर फलन f(x) की चर x के सापेक्ष परिवर्तन की दर शून्य होती है अर्थात् f'(x)=0, स्तब्ध कहलाते हैं।प्रत्येक चरम बिन्दु फलन का स्तब्ध बिन्दु होता है परन्तु प्रत्येक स्तब्ध बिन्दु चरम बिन्दु नहीं हो सकता।
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 12 में निम्नतम और उच्चतम (Minima and Maxima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Minima and Maxima in Class 12
कक्षा 12 में निम्नतम और उच्चतम
(Minima and Maxima in Class 12)
Minima and Maxima in Class 12
कक्षा 12 में निम्नतम और उच्चतम (Minima and Maxima in Class 12) के इस आर्टिकल की
थ्योरी देखने के लिए इससे पूर्व पोस्ट किए गए आर्टिकल को पढ़ना चाहिए।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.