Length of plane curves (Rectification)
1.समतल वक्रों की लम्बाई (चापकलन) का परिचय [Introduction to Length of plane curves (Rectification)]:
समतल वक्रों की लम्बाई (चापकलन) [ Length of plane curves (Rectification)]के बारे में बताया गया है।अवकलन गणित में s के अवकलन गुणांक का किन्हीं सीमाओं के मध्य समाकलन करने पर s अर्थात् समतल वक्रों की लम्बाई (चापकलन) [Length of plane curves (Rectification)] प्राप्त होता है।
सीमाओं के अन्तर्गत अवकलन गुणांक का समाकलन निश्चित समाकलन होता है।
चापकलन की परिभाषा ( Definition of Rectification)-
समतल वक्र के दो बिन्दुओं के बीच चाप की लम्बाई ज्ञात करने की विधि चापकलन कहलाती है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-coordinates of centre of curvature
2.समतल वक्रों की लम्बाई (चापकलन)[Length of plane curves (Rectification)]-
(1.)कार्तीय समीकरणों के लिए (For Cartesian equations):
यदि कोई वक्र y=f(x) के रूप का हो तो इस वक्र के किसी बिन्दु A ,जिसके लिए x=a है,से वक्र पर स्थित किसी अन्य बिन्दु P(x,y) तक के चाप की लम्बाई s हो तो अवकलन गणित से हम लिख सकते हैं कि
\frac { ds }{ dx } =\left\{ 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } \right\}
उपर्युक्त अवकल गुणांक का सीमाओं a से x के मध्य समाकलन करने पर
\int _{ a }^{ x }{ \frac { ds }{ dx } } dx=\int _{ a }^{ x }{ \sqrt { 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } } } dx\\ s=\int _{ a }^{ x }{ \sqrt { 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } } } dx
अतः वक्र पर स्थित दो बिन्दुओं A तथा B के भुज (abscissae) क्रमशः a तथा b हो तो चाप AB की लम्बाई निम्न प्रकार ज्ञात की जा सकती है-
s=\int _{ a }^{ b }{ \sqrt { 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } } } dx
(2.) कार्तीय समीकरण का दूसरा रूप (Another form of Cartesian equation):
यदि कार्तीय समीकरण x=f(y) के रूप का हो तो इस स्थिति में समतल वक्रों की लम्बाई (चापकलन) [Length of plane curves (Rectification)] निम्न प्रकार ज्ञात की जा सकती है-
\frac { ds }{ dy } =\sqrt { 1+{ \left( \frac { dx }{ dy } \right) }^{ 2 } }
यदि वक्र पर स्थित दो बिन्दुओं A तथा B की कोटियां क्रमशः c व d हो तो चाप AB की लम्बाई इन सीमाओं के मध्य समाकलन करके ज्ञात की जा सकती है।
s=\int _{ c }^{ d }{ \sqrt { 1+{ \left( \frac { dx }{ dy } \right) }^{ 2 } } } dy
(3.)प्राचलिक समीकरणों के लिए (For parametric equations):
यदि x तथा y को किसी प्राचल के पदों में व्यक्त किया गया हो तो समतल वक्रों की लम्बाई (चापकलन) [Length of plane curves (Rectification)] निम्न प्रकार ज्ञात की जा सकती है (प्राचलिक समीकरण x=f(t),
\frac { ds }{ dt } =\sqrt { { \left( \frac { dx }{ dt } \right) }^{ 2 }+{ \left( \frac { dy }{ dt } \right) }^{ 2 } }
अतः वक्र पर स्थित दो बिन्दुओं A तथा B के लिए प्राचल t के मान क्रमशः { t }_{ 1 } तथा{ t }_{ 2 } हो तो चाप AB की लम्बाई होगी-
s=\int _{ { t }_{ 1 } }^{ { t }_{ 2 } }{ \sqrt { { \left( \frac { dx }{ dt } \right) }^{ 2 }+{ \left( \frac { dy }{ dt } \right) }^{ 2 } } } dt
(4.)ध्रुवीय समीकरणों के लिए (For polar equations):
यदि ध्रुवीय समीकरण r=f\left( \theta \right) के रूप का हो तो समतल वक्रों की लम्बाई (चापकलन) [ Length of plane curves (Rectification)] निम्न प्रकार ज्ञात की जा सकती है-
\frac { ds }{ dt } =\sqrt { { r }^{ 2 }+{ \left( \frac { dr }{ d\theta } \right) }^{ 2 } }
यदि वक्र पर स्थित दो बिन्दुओं A तथा B के सदिश कोण क्रमशः \alpha तथा\beta हो तो चाप AB की लम्बाई होगी-
s=\int _{ \alpha }^{ \beta }{ \sqrt { { r }^{ 2 }+{ \left( \frac { dr }{ d\theta } \right) }^{ 2 } } } d\theta
(5.) ध्रुवीय समीकरण का दूसरा रूप (Another form of polar equation):
यदि ध्रुवीय समीकरण \theta =f\left( r \right) के रूप का हो तो समतल वक्रों की लम्बाई (चापकलन)[Length of plane curves (Rectification)] निम्न प्रकार ज्ञात की जा सकती है-
\frac { ds }{ dr } =\sqrt { 1+{ r }^{ 2 }{ \left( \frac { d\theta }{ dr } \right) }^{ 2 } }
अतः यदि वक्र पर स्थित दो बिन्दुओं A तथा B के ध्रुवान्तर क्रमशः { r }_{ 1 } तथा { r }_{ 2 } हो तो AB की लम्बाई होगी-
s=\int _{ { r }_{ 1 } }^{ { r }_{ 2 } }{ \sqrt { 1+{ r }^{ 2 }{ \left( \frac { d\theta }{ dr } \right) }^{ 2 } } } dr
(6.)पदिक समीकरण के लिए (For the pedal equation):
पदिक समीकरण के रूप का हो तथा वक्र पर स्थित दो बिन्दुओं A तथा B के ध्रुवान्तर (radius vectors) क्रमशः { r }_{ 1 } तथा { r }_{ 2 } हो तो AB चाप की लम्बाई होगी
s=\int _{ { r }_{ 1 } }^{ { r }_{ 2 } }{ \frac { rdr }{ \sqrt { { r }^{ 2 }-p^{ 2 } } } }
Question-1. प्रथम पाद में परवलय { y }^{ 2 }-4y+2x=0 के चाप की लम्बाई ज्ञात कीजिए।(Find the length of the arc of the parabola { y }^{ 2 }-4y+2x=0which lies in the first quadrant).
Solution:
{ y }^{ 2 }-4y+2x=0
y के सापेक्ष अवकलन करने पर-
2y-4+2\frac { dx }{ dy } =0\\ \frac { dx }{ dy } =2-y
चाप की लम्बाई के लिए सीमा ज्ञात करने हेतु x=0 रखने पर
{ y }^{ 2 }-4y=0\\ y\left( y-4 \right) =0\\ y=0,y=4
अतः चाप की लम्बाई s=\int _{ 0 }^{ 4 }{ \sqrt { 1+{ \left( \frac { dx }{ dy } \right) }^{ 2 } } } dy\\ s=\int _{ 0 }^{ 4 }{ \sqrt { 1+{ \left( 2-y \right) }^{ 2 } } } dy\\ s=\int _{ 0 }^{ 4 }{ \sqrt { 1+{ \left( y-2 \right) }^{ 2 } } } dy\\ s={ { \left[ \frac { y-2 }{ 2 } \sqrt { 1+{ \left( y-2 \right) }^{ 2 } } +\frac { 1 }{ 2 } \log { \left\{ y-2+\sqrt { 1+{ \left( y-2 \right) }^{ 2 } } \right\} } \right] }^{ 4 } }_{ 0 }\\ s=\sqrt { 5 } +\frac { 1 }{ 2 } \log { \left\{ 2+\sqrt { 5 } \right\} } +\sqrt { 5 } -\frac { 1 }{ 2 } \log { \left\{ \sqrt { 5 } -2 \right\} } \\ s=2\sqrt { 5 } +\frac { 1 }{ 2 } \log { \left\{ \frac { 2+\sqrt { 5 } }{ \sqrt { 5 } -2 } \right\} } \\ s=2\sqrt { 5 } +\frac { 1 }{ 2 } \log { { \left( \sqrt { 5 } +2 \right) }^{ 2 } } \\ s=2\sqrt { 5 } +\log { \left( \sqrt { 5 } +2 \right) }
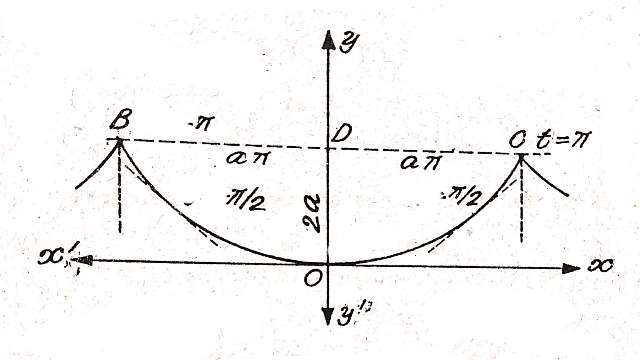
Question-2.सिद्ध कीजिए कि साइक्लाइड x=a\left( \theta -sin\theta \right) \quad \quad \quad \quad \quad \quad ,y=a\left( 1-cos\theta \right) के महराब की लम्बाई 8a है।( Prove that the length of an arc of the cycloid x=a\left( \theta -sin\theta \right) \quad \quad \quad \quad \quad \quad ,y=a\left( 1-cos\theta \right) is 8a.)
Solution:
x=a\left( \theta -sin\theta \right) \quad \quad \quad \quad \quad \quad ,y=a\left( 1-cos\theta \right) \\ \frac { dx }{ d\theta } =a\left( 1-cos\theta \right) \quad \quad \quad ,\frac { dy }{ d\theta } =a\quad sin\theta
चाप की लम्बाई के लिए सीमाएं y=0 रखने पर ज्ञात की जा सकती है-
a\left( 1-cos\theta \right) =0\\ cos\theta =1\\ \theta =\pi
अतः चाप की लम्बाई=2× चाप की लम्बाई
s=2\times \int _{ 0 }^{ \pi }{ \sqrt { { \left( \frac { dx }{ d\theta } \right) }^{ 2 }+{ \left( \frac { dy }{ d\theta } \right) }^{ 2 } } } d\theta \\ s=2\times \int _{ 0 }^{ \pi }{ \sqrt { { \left\{ a\left( 1-cos\theta \right) \right\} }^{ 2 }+{ \left\{ a\quad sin\theta \right\} }^{ 2 } } } d\theta \\ s=2\times \int _{ 0 }^{ \pi }{ \sqrt { { { a }^{ 2 }\left( 1-cos\theta \right) }^{ 2 }+{ a }^{ 2 }{ sin }^{ 2 }\theta } } d\theta \\ s=2a\times \int _{ 0 }^{ \pi }{ \sqrt { 1-2cos\theta +cos^{ 2 }\theta +{ sin }^{ 2 }\theta } } d\theta \\ s=2a\times \int _{ 0 }^{ \pi }{ \sqrt { 2-2cos\theta } } d\theta \\ s=2\sqrt { 2 } a\times \int _{ 0 }^{ \pi }{ \sqrt { 1-cos\theta } } d\theta \\ s=2\sqrt { 2 } a\times \int _{ 0 }^{ \pi }{ \sqrt { 2{ sin }^{ 2 }\frac { \theta }{ 2 } } } d\theta \\ s=2\sqrt { 2 } a\times \int _{ 0 }^{ \pi }{ \sqrt { 2 } sin\frac { \theta }{ 2 } } d\theta \\ s=4a\times \int _{ 0 }^{ \pi }{ sin\frac { \theta }{ 2 } } d\theta \\ s=8a\times { \left[ -2\quad cos\frac { \theta }{ 2 } \right] }_{ 0 }^{ \pi }\\ s=8a\times \left[ -2\quad cos\frac { \pi }{ 2 } +2\quad cos0 \right] \\ s=8a
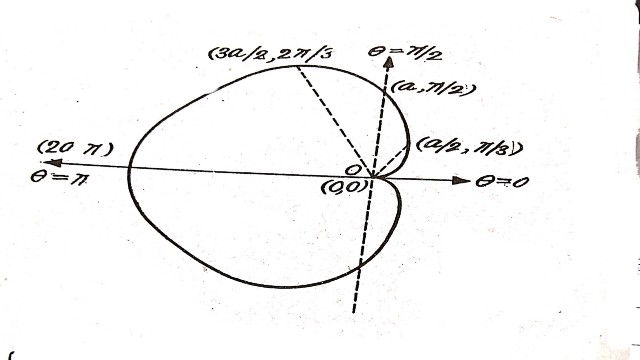
Question-3.निम्नलिखित वक्र का परिमाप ज्ञात कीजिए।(Find the perimeter of the following curve.)
r=a\left( 1-cos\theta \right)
Solution:
r=a\left( 1-cos\theta \right) \\ \frac { dr }{ d\theta } =a\quad sin\theta
परिमाप=2\int _{ 0 }^{ \pi }{ \sqrt { \left[ { r }^{ 2 }+{ \left( \frac { dr }{ d\theta } \right) }^{ 2 } \right] } } d\theta \\ =2\int _{ 0 }^{ \pi }{ \sqrt { \left[ { { a }^{ 2 }\left( 1-cos\theta \right) }^{ 2 }+{ a }^{ 2 }sin^{ 2 }\theta \right] } } d\theta \\ =2\int _{ 0 }^{ \pi }{ \sqrt { 1-2cos\theta +cos^{ 2 }\theta +{ sin }^{ 2 }\theta } } d\theta \\ =2a\times \int _{ 0 }^{ \pi }{ \sqrt { 1-2cos\theta +cos^{ 2 }\theta +{ sin }^{ 2 }\theta } } d\theta \\ =2\sqrt { 2 } a\times \int _{ 0 }^{ \pi }{ \sqrt { 1-cos\theta } } d\theta
उपर्युक्त उदाहरणों की सहायता से समतल वक्रों की लम्बाई (चापकलन) [ Length of plane curves (Rectification)]को समझा जा सकता है।
Also Read This Article:-Perpendicular length pole on tangent
Length of plane curves (Rectification)
समतल वक्रों की लम्बाई (चापकलन) [ Length of plane curves (Rectification)]
Length of plane curves (Rectification)
समतल वक्रों की लम्बाई (चापकलन) [ Length of plane curves (Rectification)]के बारे में बताया गया है।अवकलन गणित में s के अवकलन गुणांक का किन्हीं सीमाओं के मध्य समाकलन करने पर s अर्थात् समतल वक्रों की लम्बाई (चापकलन) [Length of plane curves (Rectification)] प्राप्त होता है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |