coordinates of centre of curvature
1.वक्रता केन्द्र के निर्देशांक का परिचय (Introduction to coordinates of centre of curvature):
वक्रता केन्द्र के निर्देशांक(coordinates of centre of curvature) को समझने के लिए वक्रता केन्द्र को समझना आवश्यक है।जब तक हमें किसी थ्योरी की बेसिक बातों की जानकारी नहीं होती है तब तक वह थ्योरी समझ में नहीं आती है।
वक्रता केन्द्र ( centre of curvature):
(1.) किसी समतल वक्र के किसी बिन्दु से जाने वाले उस वृत्त का केन्द्र जिसकी त्रिज्या उस बिन्दु पर वक्र की वक्रता का व्युत्क्रम हो।
(2.)किसी पृष्ठ के किसी बिन्दु P के सन्दर्भ में,P और Q से खींचे गए पृष्ठ के अभिलम्बों का प्रतिच्छेद बिन्दु जहां बिन्दु Q बिन्दु P का सन्निकट बिन्दु है और सीमान्त स्थिति में उसकी प्रवृत्ति P से संपाती होने की है।
(3.)किसी वक्र के किसी बिन्दु P पर वक्रता केन्द्र वह बिन्दु कहलाता है जो कि P पर अभिलम्बों का प्रतिच्छेदक दिशा में उससे \rho दूरी पर होता है।
साधारण शब्दों में किसी वक्र के किसी बिन्दु P व Q पर खींचे गए अभिलम्बों का प्रतिच्छेद बिन्दु वक्रता केन्द्र होता है।
Also Read This Article:-Radius and centre of a circle in plane section of sphere
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
2.वक्रता केन्द्र के निर्देशांक (Coordinates of Centre of curvature):
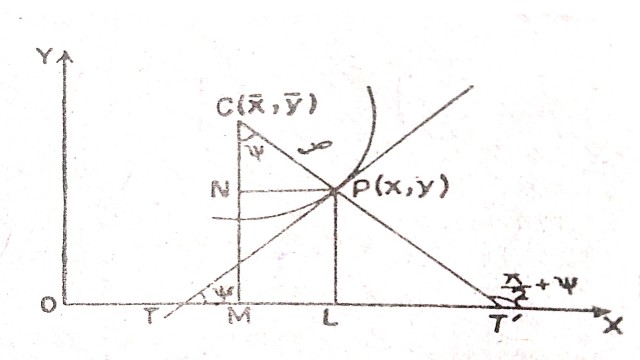
माना कि वक्र का समीकरण y=f(x) है।इस वक्र पर कोई बिन्दु P(x,y) लीजिए।यह भी मान लो कि वक्रता केन्द्र C(x,y) है, इसलिए PC=\rho ,वक्रता त्रिज्या है।
साथ ही माना कि P पर स्पर्श रेखा की धन दिशा x-अक्ष के साथ\psi कोण बनाती है, इसलिए अभिलम्ब की धनात्मक दिशा x-अक्ष के साथ\left( \frac { \Pi }{ 2 } +\psi \right) कोण बनाएगी।
अब x-अक्ष पर लम्ब PL व CM तथा CM रेखा पर PN लम्ब खींचों।
चित्रानुसार
\bar { x } =OM=OL-ML\\ \quad \quad \quad =OL-PL\\ \quad \quad \quad =x-\rho \quad sin\psi ........(1)\\ \bar { y } =CM=MN+NC\\ \quad \quad \quad =PL+NC\\ \quad \quad \quad =y+\rho \quad cos\psi ........(2)
अब \rho,sin\psi ,cos\psi के मान (1) तथा (2) में प्रतिस्थापित करने पर
\bar { x } =x-\frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { y }_{ 2 } } \times \frac { 1 }{ \sqrt { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } } \\ \bar { x } =x-{ y }_{ 1 }\left( \frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } }{ { y }_{ 2 } } \right) \\ \bar { y } =y+\frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { y }_{ 2 }\sqrt { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } } \\ \\ \bar { y } =y+\frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) }^{ \frac { 3 }{ 2 } } }{ { y }_{ 2 } }
उदाहरण -निम्न वक्रों के सम्मुख प्रदर्शित बिन्दुओं पर वक्रता केंद्रों को ज्ञात कीजिए
{ x }^{ 3 }+{ y }^{ 3 }=3axy\quad ;\quad (\frac { 3a }{ 2 } ,\frac { 3a }{ 2 } )
solution:-{ x }^{ 3 }+{ y }^{ 3 }=3axy\\ { 3x }^{ 2 }+{ 3y }^{ 2 }\frac { dy }{ dx } -3ay+3ax\frac { dy }{ dx } \\ { 3y }^{ 2 }\frac { dy }{ dx } -3ax\frac { dy }{ dx } =3ay-{ 3x }^{ 2 }\\ 3\left( { y }^{ 2 }-ax \right) \frac { dy }{ dx } =\left( ay-{ x }^{ 2 } \right) \\ \frac { dy }{ dx } =\frac { ay-{ x }^{ 2 } }{ { y }^{ 2 }-ax } \\ { \left( \frac { dy }{ dx } \right) }_{ (\frac { 3a }{ 2 } ,\frac { 3a }{ 2 } ) }=\frac { a{ \left( \frac { 3a }{ 2 } \right) }-{ \left( \frac { 3a }{ 2 } \right) }^{ 2 } }{ { \left( \frac { 3a }{ 2 } \right) }^{ 2 }-a\left( \frac { 3a }{ 2 } \right) } \\ { \left( \frac { dy }{ dx } \right) }_{ (\frac { 3a }{ 2 } ,\frac { 3a }{ 2 } ) }=\frac { \frac { { 3a }^{ 2 } }{ 2 } -\frac { { 9a }^{ 2 } }{ 4 } }{ \frac { { 9a }^{ 2 } }{ 4 } -\frac { { 3a }^{ 2 } }{ 2 } } \\ { \left( \frac { dy }{ dx } \right) }_{ (\frac { 3a }{ 2 } ,\frac { 3a }{ 2 } ) }=\frac { \frac { { 6a }^{ 2 }-{ 9a }^{ 2 } }{ 4 } }{ \frac { { 9a }^{ 2 }-{ 6a }^{ 2 } }{ 4 } } \\ { \left( \frac { dy }{ dx } \right) }_{ (\frac { 3a }{ 2 } ,\frac { 3a }{ 2 } ) }=\frac { { -3a }^{ 2 } }{ { 3a }^{ 2 } } \\ { { y }_{ 1 }=\left( \frac { dy }{ dx } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=-1\\ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =\frac { \left( { y }^{ 2 }-ax \right) \left( a\frac { dy }{ dx } -2x \right) -\left( ay-{ x }^{ 2 } \right) \left( 2y\frac { dy }{ dx } -a \right) }{ { \left( { y }^{ 2 }-ax \right) }^{ 2 } }\\ { \left( \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { \left[ { \left( \frac { 3a }{ 2 } \right) }^{ 2 }-a{ \left( \frac { 3a }{ 2 } \right) } \right] \left[ a\left( -1 \right) -2\left( \frac { 3a }{ 2 } \right) \right] -\left[ a\left( \frac { 3a }{ 2 } \right) -{ \left( \frac { 3a }{ 2 } \right) }^{ 2 } \right] \left[ 2\left( \frac { 3a }{ 2 } \right) \left( -1 \right) -a \right] }{ { \left[ { \left( \frac { 3a }{ 2 } \right) }^{ 2 }-a{ \left( \frac { 3a }{ 2 } \right) } \right] }^{ 2 } }\\ { \left( \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { \left( \frac { { 9a }^{ 2 }-{ 6a }^{ 2 } }{ 4 } \right) \left( -4a \right) -\left( \frac { { 3a }^{ 2 } }{ 2 } -\frac { { 9a }^{ 2 } }{ 4 } \right) \left( 9a-a \right) }{ { \left[ \frac { { 9a }^{ 2 }-{ 6a }^{ 2 } }{ 4 } \right] }^{ 2 } } \\ { \left( \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { -12{ a }^{ 3 }-\left( \frac { { -3a }^{ 2 } }{ 4 } \right) \left( 8a \right) }{ { \left( \frac { { 3a }^{ 2 } }{ 4 } \right) }^{ 2 } } \\ { \left( \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \right) }_{ \left( \frac { 3a }{ 2 } ,\frac { 3a }{ 2 } \right) }=\frac { -12{ a }^{ 3 }+{ 6a }^{ 3 } }{ { \frac { { 9a }^{ 4 } }{ 16 } } } =\frac { { 6a }^{ 3 }\times 16 }{ { 9a }^{ 4 } } \\ { y }_{ 2 }=\frac { -32 }{ 3a } \\ \\
वक्रता केंद्र के निर्देशांक (coordinates of centre of curvature):
\bar { x } =x-{ y }_{ 1 }\left( \frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } }{ { y }_{ 2 } } \right) \\ \bar { x } =\frac { 3a }{ 2 } -\frac { (-1)\left[ 1+{ (-1) }^{ 2 } \right] }{ \left( \frac { -32 }{ 3a } \right) } \\ \bar { x } =\frac { 3a }{ 2 } -2\times \frac { 3a }{ 32 } \\ \bar { x } =\frac { 3a }{ 2 } -\frac { 3a }{ 16 } \\ \bar { x } =\frac { 24a-3a }{ 16 } \\ \bar { x } =\frac { 21a }{ 16 } \\ \bar { y } =y+\frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } }{ { y }_{ 2 } } \\ \bar { y } =y+\frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } }{ { y }_{ 2 } } \\ \bar { y } =\frac { 3a }{ 2 } +\frac { { \left( 1+{ (-1) }^{ 2 } \right) } }{ \left( \frac { -32 }{ 3a } \right) } \\ \bar { y } =\frac { 3a }{ 2 } -2\times \frac { 3a }{ 32 } \\ \bar { y } =\frac { 3a }{ 2 } -\frac { 3a }{ 16 } \\ \bar { y } =\frac { 24a-3a }{ 16 } \\ \bar { y } =\frac { 21a }{ 16 } \\ \left( \bar { x } ,\bar { y } \right) =\left( \frac { 21a }{ 16 } ,\frac { 21a }{ 16 } \right)
(b)\frac { x^{ 2 } }{ a^{ 2 } } -\frac { y^{ 2 } }{ b^{ 2 } } =1
solution:-\frac { x^{ 2 } }{ a^{ 2 } } -\frac { y^{ 2 } }{ b^{ 2 } } =1\\ \frac { 2x }{ a^{ 2 } } -\frac { 2y }{ b^{ 2 } } \frac { dy }{ dx } =0\\ { y }_{ 1 }=\frac { dy }{ dx } =\frac { b^{ 2 }x }{ a^{ 2 }y } \\ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =\frac { b^{ 2 } }{ a^{ 2 } } \left( \frac { y.1-x\frac { dy }{ dx } }{ { y }^{ 2 } } \right) .\\ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =\frac { b^{ 2 } }{ a^{ 2 } } \left( \frac { y-x\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } }{ { y }^{ 2 } } \right) \\ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =\frac { b^{ 2 } }{ a^{ 2 } } \left( \frac { a^{ 2 }{ y }^{ 2 }-b^{ 2 }x^{ 2 } }{ a^{ 2 }{ y }^{ 3 } } \right) \\ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =\frac { b^{ 2 } }{ a^{ 4 }{ y }^{ 3 } } \left( -a^{ 2 }b^{ 2 } \right) \\ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =-\frac { b^{ 4 } }{ a^{ 2 }{ y }^{ 3 } } \\
वक्रता केंद्र के निर्देशांक (coordinates of centre of curvature)-
\bar { x } =x-\frac { { { y }_{ 1 }\left( 1+{ { y }_{ 1 } }^{ 2 } \right) } }{ { y }_{ 2 } } \\ \bar { x } =x-\frac { { b }^{ 2 }x }{ { a }^{ 2 }y } \frac { { \left( 1+{ \left( \frac { { d }^{ 2 }x }{ { a }^{ 2 }y } \right) }^{ 2 } \right) } }{ -\frac { b^{ 4 } }{ { a }^{ 2 }{ y }^{ 3 } } } \\ \bar { x } =x+\frac { b^{ 2 }x }{ { a }^{ 2 }y } \frac { { a }^{ 2 }{ y }^{ 3 } }{ b^{ 4 } } { \left( \frac { { a }^{ 4 }{ b }^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } }{ { a }^{ 4 }{ y }^{ 2 } } \right) }\\ \bar { x } =x+\frac { x }{ { a }^{ 4 }{ b }^{ 2 } } { \left( { a }^{ 4 }{ y }^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } \right) }\\
or\\ \bar { x } =x+\frac { x }{ { a }^{ 4 }{ b }^{ 2 } } { \left( { a }^{ 4 }{ y }^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } \right) }\left[ { a }^{ 4 }\left( \frac { x^{ 2 } }{ a^{ 2 } } -1 \right) { b }^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } \right] \\ \bar { x } =x+\frac { x }{ { a }^{ 4 }{ b }^{ 2 } } { \left( { a }^{ 4 }{ y }^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } \right) }\left[ { a^{ 2 }{ b }^{ 2 }{ x }^{ 2 }-{ a }^{ 4 } }{ b }^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } \right] \\
or\bar { x } =x+\frac { x }{ { a }^{ 4 } } \left[ { a^{ 2 }{ x }^{ 2 }-{ a }^{ 4 } }+{ b }^{ 2 }{ x }^{ 2 } \right] \\ \bar { x } =\frac { \left[ { a }^{ 4 }x+{ a^{ 2 }{ x }^{ 3 }-{ a }^{ 4 }x }+{ b }^{ 2 }{ x }^{ 3 } \right] }{ { a }^{ 4 } } \\ \bar { x } =\frac { \left[ { a^{ 2 }+ }{ b }^{ 2 } \right] }{ { a }^{ 4 } } { x }^{ 3 }\\ \bar { y } =y+\frac { { \left( 1+{ { y }_{ 1 } }^{ 2 } \right) } }{ { y }_{ 2 } } \\ \bar { y } =y+\frac { \left[ 1+{ \left( \frac { { b }^{ 2 }x }{ { a }^{ 2 }y } \right) }^{ 2 } \right] }{ -\frac { b^{ 4 } }{ { a }^{ 2 }{ y }^{ 3 } } } \\ \bar { y } =y-\frac { { a }^{ 2 }{ y }^{ 3 } }{ b^{ 4 } } { \left( \frac { { a }^{ 4 }y^{ 2 }+{ b }^{ 4 }{ x }^{ 2 } }{ a^{ 4 }{ y }^{ 2 } } \right) }\\ \bar { y } =y-\frac { b }{ b^{ 4 }{ a }^{ 2 } } { \left[ { a }^{ 4 }y^{ 2 }+{ b }^{ 4 }\left( \frac { { y }^{ 2 } }{ { b }^{ 2 } } +1 \right) { a }^{ 2 } \right] }\\ \bar { y } =y-\frac { y }{ b^{ 4 }{ a }^{ 2 } } { \left[ { a }^{ 4 }y^{ 2 }+{ a }^{ 2 }{ b }^{ 2 }{ y }^{ 2 }+{ a }^{ 2 }{ b }^{ 4 } \right] }\\ \bar { y } =y-\frac { y }{ { a }^{ 2 }b^{ 4 } } \times { { a }^{ 2 }\left[ { a }^{ 2 }y^{ 2 }+{ b }^{ 2 }{ y }^{ 2 }+{ b }^{ 4 } \right] }\\ \bar { y } =y-\frac { y }{ b^{ 4 } } { \left[ { a }^{ 2 }y^{ 2 }+{ b }^{ 2 }{ y }^{ 2 }+{ b }^{ 4 } \right] }\\ \bar { y } =\frac { { \left[ b^{ 4 }y-{ a }^{ 2 }y^{ 3 }-{ b }^{ 2 }{ y }^{ 3 }-{ b }^{ 4 }y \right] } }{ b^{ 4 } } \\ \bar { y } =-\frac { \left[ { a^{ 2 }+ }{ b }^{ 2 } \right] }{ b^{ 4 } } { y }^{ 3 }\\
वक्रता केंद्र के निर्देशांक(coordinates of centre of curvature) :
\left( \bar { x } ,\bar { y } \right) =\left[ \frac { \left[ { a^{ 2 }+ }{ b }^{ 2 } \right] }{ a^{ 4 } } { x }^{ 3 },-\frac { \left[ { a^{ 2 }+ }{ b }^{ 2 } \right] }{ b^{ 4 } } { y }^{ 3 } \right]
Also Read This Article:-Radius of Curvature(differential calculus)
उपर्युक्त आर्टिकल में वक्रता केन्द्र के निर्देशांक (coordinates of centre of curvature) के बारे में बताया गया है.
2.वक्रता केन्द्र के निर्देशांक (coordinates of centre of curvature) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.वक्रता त्रिज्या का सूत्र क्या है? (What is the formula for radius of curvature?):
उत्तर:R= 1/K,जहां R वक्रता त्रिज्या है और K वक्रता है।
प्रश्न:2.किस वक्र को वक्रता केंद्र के स्थान के रूप में परिभाषित किया गया है? (Which curve is defined as the locus of centre of curvature?):
उत्तर:केन्द्रज (Evolute): वक्र के केन्द्रज (Evolute) को उस वक्र के वक्रता केंद्र के स्थान के रूप में परिभाषित किया जाता है।प्रतिकेन्द्रज (Involute) :यदि C’ वक्र C का केन्द्रज है तो C वक्र C’ का प्रतिकेन्द्रज कहलाता है।
प्रश्न:3.भौतिकी में वक्रता का केंद्र क्या है? (What is centre of curvature in physics?):
उत्तर:ज्यामिति में,वक्र का वक्रता केंद्र (center of curvature) एक ऐसे बिंदु पर पाया जाता है जो वक्र से अभिलम्ब सदिश (normal vector) पर स्थित वक्रता त्रिज्या के बराबर दूरी पर होता है।वक्रता शून्य होने पर यह अनंत का बिंदु है।वक्र के लिए दोलन वृत्त (osculating circle) वक्रता के केंद्र पर केंद्रित होता है।
प्रश्न:4.वक्र की वक्रता त्रिज्या क्या है? (What is radius of curvature of a curve?):
उत्तर:अवकल ज्यामिति में,वक्रता त्रिज्या R,वक्रता का व्युत्क्रम (reciprocal) है।एक वक्र के लिए,यह वृत्ताकार चाप की त्रिज्या के बराबर होता है जो उस बिंदु पर वक्र का सबसे अच्छा अनुमान (best approximates) लगाता है।समतलों (surfaces) के लिए,वक्रता त्रिज्या एक वृत्त की त्रिज्या है जो एक लम्बवत खंड (normal section) या उसके संयोजन के लिए सबसे उपयुक्त है।
वक्र के बिंदु (1,1) पर वक्रता त्रिज्या की गणना करें जिसका समीकरण x^3-2xy + y^3 =0 है और इसलिए वक्रता केंद्र के निर्देशांक प्राप्त करें।x = 1 + sinθ और y = sinθ−1 2 cos 2θ और इसलिए वक्रता केंद्र के निर्देशांक प्राप्त करें। ρ = 43.6705, (xc,yc)=(42.333,8.417)।
प्रश्न:5.वक्रता केंद्र का दूसरा नाम क्या है? (What is the another name of centre of curvature?):
उत्तर:समानार्थी शब्द।वक्रता केंद्र (center of curvature midpoint centre center) मध्यबिंदु केंद्र (midpoint centre) केंद्र (center)।इनफील्ड पेरिफेरल राइट लेफ्ट (infield peripheral right left)।
प्रश्न:6.सरल शब्दों में वक्रता का केंद्र क्या है? (What is centre of curvature in simple words?):
उत्तर:वृत्त का केंद्र जिसका केंद्र वक्र के किसी दिए गए बिंदु के अभिलंब (normal) पर एक वक्र के अवतल भुजा (concave side) पर स्थित होता है और जिसकी त्रिज्या उस बिंदु पर वक्रता की त्रिज्या के बराबर होती है।
प्रश्न:7.आप वक्रता की गणना कैसे करते हैं? (How do you calculate curvature?):
उत्तर:एक बिंदु M(x,y) पर वक्र की वक्रता त्रिज्या को इस बिंदु पर वक्र के वक्रता K का व्युत्क्रम (inverse) कहा जाता है: R=1/K।इसलिए स्पष्ट समीकरण y=f(x) द्वारा दिए गए समतल वक्रों के लिए,एक बिंदु M(x,y) पर वक्रता की त्रिज्या निम्नलिखित व्यंजक द्वारा दी जाती है: R=\frac{1+(y′(x))^2]^3/2}{y′′(x)} ।
प्रश्न:8.मुख्य फोकस और वक्रता केंद्र क्या है? (What is principal focus and centre of curvature?):
उत्तर:गोलाकार दर्पण के ध्रुव (pole),वक्रता केंद्र (centre of curvature),वक्रता त्रिज्या (radius of curvature),मुख्य अक्ष (principal axis),छिद्र (aperture),फोकस (focus) और फोकस दूरी (focal length) को परिभाषित करें।
वक्रता त्रिज्या: गोले की त्रिज्या जिसका दर्पण भाग बनाता है।”R” द्वारा दर्शाया गया है।मुख्य अक्ष: ध्रुव (P) और वक्रता केंद्र को मिलाने वाली सीधी रेखा।
प्रश्न:9.वक्रता और ध्रुव का केंद्र क्या है? (What is the centre of curvature and pole?):
उत्तर : ध्रुव (Pole)-दर्पण के ज्यामितीय केंद्र को ध्रुव कहते हैं।एपर्चर (aperture) AB का मध्य बिंदु P है, P दर्पण का ध्रुव है।वक्रता केंद्र (Centre of curvature)-यह खोखले गोले का केंद्र होता है जिसका एक हिस्सा दर्पण होता है।
प्रश्न:10.वक्रता केंद्र मुख्य अक्ष को चित्र के माध्यम से समझा सकते हैं? (Can explain centre of curvature, principal axis through diagrams.?):
उत्तर:वक्रता केंद्र उस गोले का केंद्र बिंदु है जिससे गोलाकार दर्पण (spherical mirror) प्राप्त किया गया है।वक्रता केंद्र से दर्पण की दूरी को वक्रता त्रिज्या के रूप में जाना जाएगा।
आरेख के माध्यम से वक्रता केंद्र,प्रमुख अक्ष की व्याख्या कर सकते हैं।
वक्रता केंद्र उस गोले का केंद्र बिंदु है जिससे गोलाकार दर्पण प्राप्त किया गया है।वक्रता केंद्र से दर्पण की दूरी को वक्रता त्रिज्या के रूप में जाना जाएगा।
उपर्युक्त प्रश्नों के उत्तर द्वारा वक्रता केन्द्र के निर्देशांक (coordinates of centre of curvature) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा वक्रता केन्द्र के निर्देशांक (coordinates of centre of curvature) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
