1.परिक्रमण ठोसों का आयतन ज्ञात करना (Finding Volume of Solids of Revolution),परिक्रमण ठोसों का आयतन (Volume of Solids of Revolution):

• परिक्रमण ठोसों का आयतन ज्ञात करना (Finding Volume of Solids of Revolution) कि जब एक समतल क्षेत्र (Plane Area) इसके समतल में स्थित एक स्थिर रेखा के सापेक्ष परिक्रमा करता है तो यह ठोस का जनन (Generate) करता है।उदाहरणार्थ जब एक अर्धवृत्ताकार पटल (Semi-Circular Lamina) इसके सीमक अक्ष (bounding diameter) के सापेक्ष (परित:) परिक्रमा करता है तो यह ठोस गोले (Solid Sphere) का जनन करता है।
• आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
  

Also Read This Article:Volume of Solids of Revolution

2.परिक्रमण ठोसों का आयतन ज्ञात करना पर आधारित उदाहरण (Examples Based on Finding Volume of Solids of Revolution):

Example:1.प्रदर्शित कीजिए कि त्रिज्या r के गोले का आयतन {\frac{4}{3}}{\pi} r^{3} होता है।
(Show that the volume of a sphere of radius r is {\frac{4}{3}}{\pi} r^{3}.)
Solution:x अक्ष के परित वृत्त को घुमाने पर गोला जनित होता है।अतः
x^{2}+y^{2}=r^{2}
\Rightarrow{y^{2}}=r^{2}-x^{2}
अतः अभीष्ट आयतन=2{\pi}{\int_{0}^{r}}y^{2}{dx}
=2{\pi}{\int_{0}^{r}}\left(r^{2}-x^{2}\right)dx
=2{\pi}\left[r^{2}x-\frac{x^{3}}{3}\right]_{0}^{r}

=2{\pi}\left[r^{3}-\frac{r^{3}}{3}\right]

=2{\pi}\left[\frac{{2}{\pi}^{3}}{3}\right] ={\frac{4}{3}}{\pi} r^{3}

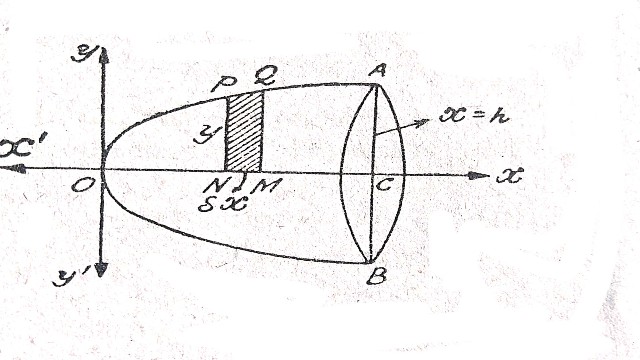
Example:2.ऊँचाई h के उस गोलीय खण्ड का आयतन ज्ञात कीजिए जो त्रिज्या a के गोले से काटा गया है। (Find the volume of a spherical cap of height h cutt off from a sphere of radius a)

Solution:गोले की सीमाएं x=a-h,x=a

अतः अभीष्ट आयतन=

{\pi}{\int_{a-h}^{a}}y^{2}dx

={\pi}{\int_{a-h}^{a}}\left(a^{2}-x^{2}\right)dx
=\left[a^{2}x-\frac{x^{3}}{3}\right]_{a-h}^{a}

={\pi}\left[a^{3}-\frac{a^{3}}{3}-a^{2}\left(a-h\right)+\frac{\left(a-h\right)^{3}}{3}\right]\\ ={\pi}\left[a^{3}-\frac{a^{3}}{3}-a^{3}+a^{2}h+\left(\frac{a^{3}}{3}-\frac{3a^{2}}{3}+\frac{3ah^{2}}{3}-h^{3}\right)\right]

={\pi}\left[-\frac{a^{3}}{3}+a^{2}h+\frac{a^{3}}{3}-\frac{3a^{2}h}{3}+\frac{3ah^{2}}{3}-\frac{h^{3}}{3}\right]

={\pi}\left[ah^{2}-\frac{h^{3}}{3}\right]

={\pi}h^{2}{\left(a-\frac{h}{3}\right)}

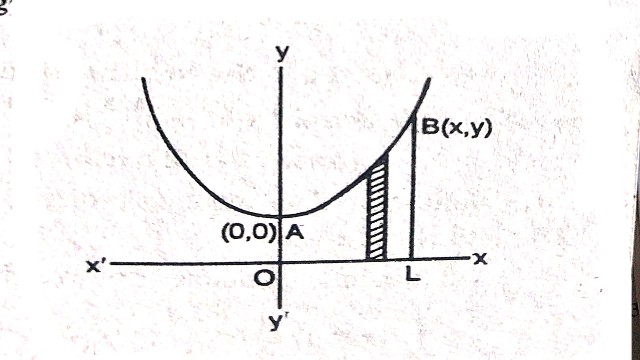
Example:3.परवलय y^{2}=4ax को x=0 से x=h तक x-अक्ष के सापेक्ष घुमाने पर जनित परवलयज का आयतन ज्ञात कीजिए। (Find the volume of a paraboloid generated by revolution about z-axis of the parabola y^{2}=4ax from x=0 to x=h)

Solution:परवलय y^{2}=4ax को x=0 से x=h तक x-अक्ष के परित घुमाने पर जनित परवलयज का अभीष्ट आयतन =

{\pi}{\int_{a}^{b}}y^{2}dx

={\pi}{\int_{0}^{h}}\left(4ax\right)dx
={\pi}4a\left[\frac{x^{2}}{2}\right]_{0}^{h}

=2{\pi}ah^{2}

Example:4.परवलय y^{2}=4ax का नाभिलम्ब द्वारा घिरा हुआ भाग नाभिलम्ब के सापेक्ष घूमता है।इस प्रकार बने ठोस का आयतन ज्ञात कीजिए। (The part of parabola y^{2}=4ax bounded by latus rectum revolves about the latus rectum.Find the volume of the solid thus formed.)

Solution:नाभिलम्ब की समीकरण=x-a तथा सीमाएं y=0,y=2a नाभिलम्ब x-अक्ष के प्रति सममित है।

अतः अभीष्ट आयतन=

2{\pi}\int_{0}^{2a}{\left(x-a\right)}^{2}dy

=2{\pi}{\int_{0}^{2a}}\left(x^{2}-2ax+a^{2}\right)dy
=2{\pi}{\int_{0}^{2a}}\left(\frac{y^{4}}{16a^{2}}-\frac{2ay^{2}}{4a}+a^{2}\right)dy
=2{\pi}{\int_{0}^{2a}}\left(\frac{y^{4}}{16a^{2}}-\frac{y^{2}}{2}+a^{2}\right)dy
=2{\pi}\left[\frac{y^{5}}{80a^{2}}-\frac{y^{3}}{6}+a^{2}y\right]_{0}^{2a}

=2{\pi}\left[\frac{32a^{5}}{80a^{2}}-\frac{8a^{3}}{6}+2a^{3}\right]

=2{\pi}\left[\frac{2a^{3}}{5}-\frac{4a^{3}}{3}+2a^{3}\right]

=2{\pi}\left[\frac{6a^{3}-20a^{3}+30a^{3}}{15}\right]

=2{\pi}×\frac{16a^{3}}{15}

={\frac{32}{15}}{\pi}a^{3}

Example:5.कैटिनरी y=\cosh\left(\frac{x}{c}\right) के एक चाप को x-अक्ष के चारों ओर घुमाने से बने ठोस का आयतन ज्ञात कीजिए। (Find the volume generated by the revolution of the catenary y=\cosh\left(\frac{x}{c}\right) about z-axis)

Solution:y=\cosh\left(\frac{x}{c}\right)

y^{2}=c^{2}\cosh^{2}{\frac{x}{c}}
y^{2}=c^{2}\left[1+\cosh{\frac{2x}{c}}\right]
\left[\cosh^{2}{\frac{x}{c}}=\frac{1+\cosh{\frac{2x}{c}}}{2}\right]

अभीष्ट आयतन=

\int_{0}^{x}{\pi}y^{2}

=\frac{{\pi}c^{2}}{2}{\int_{0}^{x}}\left[1+\cosh{\frac{2x}{c}}\right]dx
=\frac{{\pi}c^{2}}{2}{\left[x+\frac{c}{2}\sinh\left(\frac{2x}{c}\right)\right]}_{0}^{x}

=\frac{{\pi}c^{2}}{2}{\left[x+\frac{c}{2}\sinh\left(\frac{2x}{c}\right)\right]}

Example:6.वक्र x=t^{2},y={\frac{1}{3}}t^{3} के लूप को x-अक्ष के सापेक्ष घुमाने से जनित ठोस का आयतन ज्ञात कीजिए। (Find the volume generated by the revolution of the curve x=t^{2},y={\frac{1}{3}}t^{3} about x-axis)

Solution:x=t^{2},y={\frac{1}{3}}t^{3} सीमाएं ज्ञात करनेवाले हेतु y=0

t-{\frac{1}{3}}t^{3}=0
\Rightarrow{t=0,\sqrt{3}}
\frac{dx}{dt}=2t

अभीष्ट आयतन=

\int_{t=0}^{\sqrt{3}}{\pi}y^{2}dx

=\int_{0}^{\sqrt{3}}{\pi}y^{2}\left(\frac{dx}{dt}\right).dt
=\int_{0}^{\sqrt{3}}{\pi}\left(t-{\frac{1}{3}}t^{3}\right)^{2}.2t dt
=2{\pi}\int_{0}^{\sqrt{3}}\left[t^{2}-{\frac{2}{3}}t^{4}+{\frac{1}{9}}t^{6}\right]tdt
=2{\pi}\int_{0}^{\sqrt{3}}\left[t^{3}-{\frac{2}{3}}t^{5}+{\frac{1}{9}}t^{7}\right]dt
=2{\pi}\left[\frac{t^{4}}{4}-{\frac{1}{9}}t^6+{\frac{1}{72}}t^{8}\right]_{0}^{\sqrt{3}}

=2{\pi}\left[\frac{9}{4}-\frac{3}{1}+\frac{9}{8}\right]

=2{\pi}\left[\frac{18-24+9}{8}\right]

=\frac{3\pi}{4}

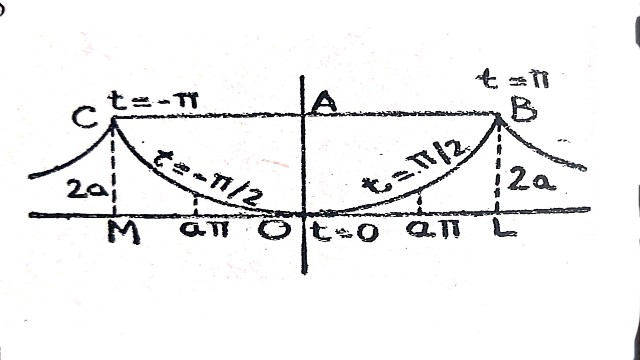
Example:7.प्रदर्शित कीजिए कि साइक्लाॅइड x=a\left({\theta}+\sin{\theta}\right),y=a\left(1-\cos{\theta}\right),0\leq{\theta}\leq{\pi} को y-अक्ष के सापेक्ष घुमाने से जनित ठोस का आयतन {\pi}a^{3}\left({\frac{3}{2}}{\pi^{2}}-\frac{8}{3}\right) है। (Show that volume of the solid generated by the revolution of the cycloid x=a\left({\theta}+\sin{\theta}\right),y=a\left(1-\cos{\theta}\right),0\leq{\theta}\leq{\pi} about the y-axis is {\pi}a^{3}\left({\frac{3}{2}}{\pi^{2}}-\frac{8}{3}\right))

Solution:x=a\left({\theta}+\sin{\theta}\right) …(1)

y=a\left(1-\cos{\theta}\right) …(2)

समीकरण (2) का \theta{} के सापेक्ष अवकलन करने पर:

\frac{dy}{\theta}=a\sin{\theta}

y-अक्ष के परित घुमाने पर जनित अभीष्ट आयतन=

\int_{0}^{\pi}{\pi}x^{2}dy

={\pi}\int_{0}^{\pi} x^{2}{\frac{dy}{d\theta}}{d\theta}
={\pi}{\int_{0}^{\pi}}a^{2}\left({\theta}+\sin{\theta}\right)^{2}a\sin{\theta}{d\theta}
{\pi}a^{3}{\int_{0}^{\pi}}\left[{\theta}^{2}\sin{\theta}+2{\theta}\sin^{2}{\theta}+\sin^{3}{\theta}\right]{d\theta}
={\pi}a^{3}{\int_{0}^{\pi}}\left[{\theta}^{2}\sin{\theta}+2{\theta}\frac{\left(1-\cos{2\theta}\right)}{2}+\frac{\left(3\sin{\theta}-\sin{3\theta}\right)}{4}\right]{d\theta}
={\pi}a^{3}{\int_{0}^{\pi}}{\theta}^{2}\sin{\theta}{d\theta}+{\pi}a^{3}{\int_{0}^{\pi}}{\theta}{d\theta}-{\pi}a^3{\int_{0}^{\pi}}{\theta}\cos{2\theta}{d\theta}+{\frac{3}{4}}{\pi}a^{3}{\int_{0}^{\pi}}\sin{\theta}{d\theta}-{\frac{1}{4}}{\pi}a^{3}{\int_{0}^{\pi}}\sin{3\theta}{d\theta}
={\pi}a^{3}{\left[-{\theta}^{2}\cos{\theta}+2{\theta}\sin{\theta}+2\cos{\theta}\right]}_{0}^{\pi}+{\frac{{\pi}a^{3}}{2}}\left[{\theta}^{2}\right]_{0}^{\pi}-{\pi}a^{3} \left[\frac{\theta}{2}\sin{2\theta}+\frac{1}{4}\cos{2\theta}\right]_{0}^{\pi}+{\frac{3}{4}}{\pi}a^{3} \left[-\cos{\theta}\right]_{0}^{\pi}-{\frac{1}{4}}{\pi}{a^{3}}\left[-\frac{\cos{3\theta}}{3}\right]_{0}^{\pi}

={\pi}a^{3} \left({\pi}^{2}-4\right){\frac{1}{2}}{\pi}a^{3} \left({\pi}^{2}\right)+{\frac{3}{4}}{\pi}a^{3}\left(2\right)+{\frac{1}{12}}{\pi}a^{3}\left(-2\right)

={\pi}a^{3}{\left[{\pi}^{2}-4+\frac{{\pi}^{2}}{2}+\frac{3}{2}-\frac{1}{6}\right]}

={\pi}a^{3}\left({\frac{3}{2}}{\pi^{2}}-\frac{8}{3}\right)

Example:8.साइक्लाॅइड x=a\left({\theta}+\sin{\theta}\right),y=a\left(1-\cos{\theta}\right) को शीर्ष पर स्पर्श रेखा के सापेक्ष घुमाने से बनी रील का आयतन है। (Show that the volume of the reel formed by the revolution of the cycloid x=a\left({\theta}+\sin{\theta}\right),y=a\left(1-\cos{\theta}\right) about the tangent at the vertex is.)

Solution:x=a\left({\theta}+\sin{\theta}\right) …(1)

y=a\left(1-\cos{\theta}\right) …(2)

समीकरण (1) का \theta{} के सापेक्ष अवकलन करने पर:

\frac{dx}{d\theta}=a\left(1+\cos{\theta}\right)
अभीष्ट आयतन=2\int_{0}^{\pi}{\pi}y^{2}dx

=2\int_{0}^{\pi}{\pi}y^{2}\left(\frac{dx}{d\theta}\right){d\theta}
=2\int_{0}^{\pi}{\pi}a^{2}\left(1-\cos{\theta}\right)^{2}.a\left(1+\cos{\theta}\right){d\theta}
=2{\pi}a^{3}\int_{0}^{\pi}\left(1-\cos{\theta}\right)^{2}.\left(1+\cos{\theta}\right){d\theta}
=2{\pi}a^{3}\int_{0}^{\pi}4\left[\sin^{2}\left(\frac{\theta}{2}\right)\right]^{2}.2\cos^{2}\left(\frac{\theta}{2}\right){d\theta}
=16{\pi}a^{3}\int_{0}^{\pi}\sin^{4}\left(\frac{\theta}{2}\right)\cos^{2}\left(\frac{\theta}{2}\right){d\theta}
put {\frac{\theta}{2}}=\phi{}
\Rightarrow{d\theta}=2{d\phi}
\text{ जब }\theta{}=0  \text{ तो }\phi{}=0
\text{ जब }\theta{}=\pi{} \text{ तो } \phi{}=\frac{\pi}{2}
=16{\pi}a^{3} \int_{0}^{\frac{\pi}{2}}\left(\sin^{4}{\phi}\cos^{2}{\phi}\right)2{d\phi}
=32{\pi}a^{3}\frac{{\Gamma{\frac{5}{2}}}{\Gamma{\frac{3}{2}}}}{2{\Gamma{4}}}
=32{\pi}a^{3}\frac{\left(\frac{3}{2}\right)\left(\frac{1}{2}\right)\sqrt{\pi}\left(\frac{1}{2}\right)\sqrt{\pi}}{2.3.2.1}
={\pi}^{2}a^{3}
निम्नलिखित वक्रों की लूपों को x-अक्ष के सापेक्ष घुमाने से बने ठोसों का आयतन ज्ञात कीजिए:
(Find the volume of solids formed by revolution of the loop of the following curves about x-axis):
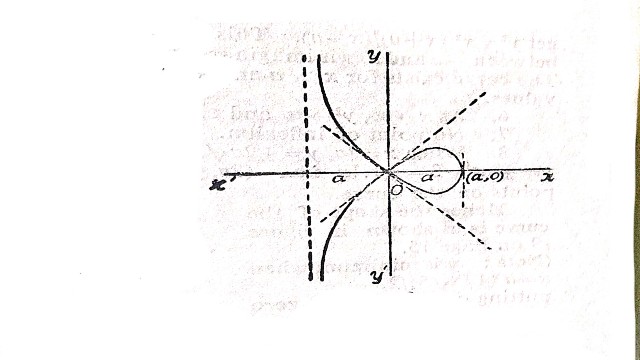
Example:9(a).y^{2}\left(a-x\right)=x^{2}\left(a+x\right)

Solution:y^{2}\left(a-x\right)=x^{2}\left(a+x\right)
सीमा के लिए y=0\Rightarrow x^{2}\left(a+x\right)=0
\Rightarrow x=0,a
अभीष्ट आयतन=\int_{-a}^{0}{\pi}y^{2}dx
={\pi}\int_{-a}^{0}{\frac{x^{2}\left(a+x\right)}{a-x}}dx
={\pi}\int_{-a}^{0}\left[-x^{2}-2ax-2a^{2}+\frac{2a^{3}}{a-x}\right]dx
={\pi}\left[-\frac{1}{3}x^{3}-2a{\frac{1}{2}}x^{2}-2a^{2}x-2a^{3}\log{\left(a-x\right)}\right]_{-a}^{0}
={\pi}\left[\left(-2a^{3}\log{a}\right)-\left\{{\frac{1}{3}}a^{3}-a^{3}+2a^{3}-2a^{3}\log{\left(2a\right)}\right\}\right]
={\pi}a^{3}\left[2\left(\log{2a}-\log{a}\right)-\left(\frac{4}{3}\right)\right]
=2{\pi}a^{3}\left[\log{2}-\left(\frac{2}{3}\right)\right]
Example:9(b).y^{2}\left(a+x\right)=x^{2}\left(3a-x\right)

Solution:y^{2}\left(a+x\right)=x^{2}\left(3a-x\right)
सीमा के लिए y=0
\Rightarrow x^{2}\left(3a-x\right)=0
\Rightarrow x=0,3a
अभीष्ट आयतन=\int_{0}^{3a}{\pi}y^{2}dx
=\int_{0}^{3a}\frac{x^{2}\left(3a-x\right)}{\left(a+x\right)}dx
=[{\pi}\int_{0}^{3a}\left[x^{2}+4ax-4a^{2}+\frac{4a^{3}}{x+a}\right]dx
={\pi}\left[-\frac{1}{3}x^{3}+2ax^{2}-4a^{2}x+4a^{3}\log\left(x+a\right)\right]_{0}^{3a}
={\pi}\left[-9a^{2}+18a^{3}-12a^{3}+4a^{3}\log{\left(4a\right)}-4a^{3}\log{a}\right]

={\pi}\left[4a^{3}\left\{\left(\log\left(4a\right)\right)-\log{a}\right\}-3a^{3}\right]

={\pi}a^{3}\left(4\log{4}-3\right)

={\pi}a^{3}\left(8\log{2}-3\right)

Exameple:9(c).y^{2}=x^{2}\left(a-x\right)

Solution:y^{2}=x^{2}\left(a-x\right) सीमा के लिए y=0 अतः x=0,a अभीष्ट आयतन=

\int_{0}^{a}{\pi}y^{2}dx

={\pi}\int_{0}^{a}x^{2}\left(a-x\right)dx
={\pi}\int_{0}^{a}x^{2}\left(a-x\right)dx
={\pi}\left[{\frac{1}{3}}ax^{3}-{\frac{1}{4}}x^{4}\right]_{0}^{a}

={\pi}\left[\frac{1}{3}-\frac{1}{4}\right]a^{4}

{\frac{\pi}{12}}a^{4}

Example:10.वक्र y\left(x^{2}+a^{2}\right)=a^{3} को इसकी अनन्तस्पर्शी के सापेक्ष घुमाने से जनित ठोसों का आयतन ज्ञात कीजिए। (Find the volume of generated by the revolution of the curve y\left(x^{2}+a^{2}\right)=a^{3} about its asymptote.)

Solution:y\left(x^{2}+a^{2}\right)=a^{3}

y=\frac{a^{3}}{\left(x^{2}+a^{2}\right)}

अभीष्ट आयतन=

\int_{-\infin{}}^{\infin{}}{\pi}y^{2}dx

={\pi}a^{6}\int_{-\infin{}}^{\infin{}}\frac{dx}{\left(a^{2}+x^{2}\right)}^{2}
=2{\pi}a^{6}\int_{0}^{\infin{}}\frac{dx}{\left(a^{2}+x^{2}\right)}^{2}
=2{\pi}a^{6}\int_{0}^{\frac{\pi}{2}}\frac{a\sec^{2}{\theta}{d\theta}}{a^{4}\left(1+\tan^{2}{\theta}\right)^{2}}
[On putting x=a\tan{\theta}]
=2{\pi}a^{3}\int_{0}^{\frac{\pi}{2}}\cos^{2}{\theta}
=2{\pi}a^{3}{\frac{1}{2}}{\frac{1}{2}}{\pi}
={\frac{1}{2}}{\pi}^{2}a^{3}
उपर्युक्त उदाहरणों के द्वारा परिक्रमण ठोसों का आयतन ज्ञात करना (Finding Volume of Solids of Revolution),परिक्रमण ठोसों का आयतन (Volume of Solids of Revolution) को समझ सकते हैं।

Also Read This Article:Lengths of Plane Curves

3.परिक्रमण ठोसों का आयतन ज्ञात करना (Finding Volume of Solids of Revolution),परिक्रमण ठोसों का आयतन (Volume of Solids of Revolution) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:

• उपर्युक्त प्रश्नों के उत्तर द्वारा परिक्रमण ठोसों का आयतन ज्ञात करना (Finding Volume of Solids of Revolution),परिक्रमण ठोसों का आयतन (Volume of Solids of Revolution) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

Finding Volume of Solids of Revolution

परिक्रमण ठोसों का आयतन ज्ञात करना
(Finding Volume of Solids of Revolution)

Finding Volume of Solids of Revolution

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here