1.द्वि-समाकल कैसे हल करते हैं?(How to solve double integrals?)-

How to solve double integrals?

द्वि-समाकल  को हल करने के लिए (to solve double integrals) द्वि-समाकल को जानना आवश्यक है।
द्वि-समाकल-प्रांत D में किसी द्विचर फलन का द्वि-समाकल है।

\int { f\left( x,y \right) } dxdy=\int _{ x=a }^{ x=b }{ \int _{ y=c }^{ y=d }{ f\left( x,y \right) } } dydx

द्वि-समाकल को हल करने के लिए (to solve double integrals) योगफल की सीमा से ज्ञात करना बहुत कठिन है। अतःद्वि-समाकल को हल करने के लिए (to solve double integrals) हम अन्य विधि से ज्ञात करेंगे।
पूर्व कक्षाओं में हमने एक चर वाले फलनों के निश्चित समाकल का मान ज्ञात करना सीखा है।इस आर्टिकल में हम दो चर वाले फलनों के निश्चित समाकल का मान ज्ञात करना सीखेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Orthogonality condition of two spheres

2.आप द्वि-समाकल की गणना कैसे करते हैं?(How do you calculate double integrals?)-

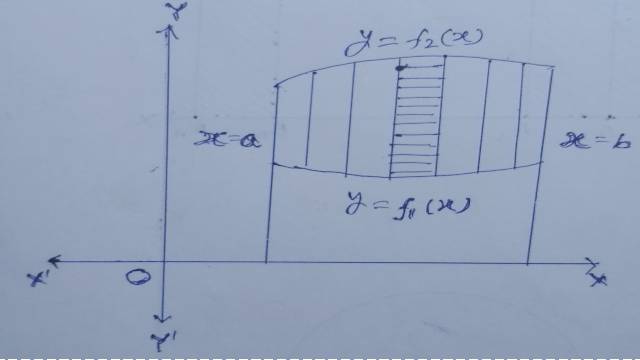
यदि वक्र y={ f }_{ 1 }\left( x \right) ,y={ f }_{ 2 }\left( x \right) ,x=a तथा x=bसे घिरा हुआ क्षेत्र A हो तो द्वि-समाकलन
(If A be the area bounded by the curves y={ f }_{ 1 }\left( x \right) ,y={ f }_{ 2 }\left( x \right) ,x=a and x=b then the double integrals)

\iint _{ A }^{ \quad }{ f\left( x,y \right) dA } =\int _{ x=a }^{ x=b }{ \int _{ { f }_{ 1 }\left( x \right) }^{ { f }_{ 2 }\left( x \right) }{ f\left( x,y \right) } } dxdy=\int _{ x=a }^{ x=b }{ \int _{ { f }_{ 1 }\left( x \right) }^{ { f }_{ 2 }\left( x \right) }{ f\left( x,y \right) } } dydx

जहां x को अचर मानकर f(x,y) का पहले y के सापेक्ष समाकलन किया जाता है।
(Where the integration is performed with respect to y treating x as constant)
क्षेत्र A को निर्देश-अक्षों (Co-ordinate axes) के समान्तर रेखाएं खींचकर आयताकार तत्त्वों में विभाजित करो जिनकी चौड़ाई \delta x तथा ऊंचाई \delta y है तब

\iint _{ A }^{ \quad }{ f\left( x,y \right) dA } =\begin{matrix} lim & \sum { \quad f\left( { x }_{ i },{ y }_{ i } \right) \delta x\delta y } \\ \delta x\rightarrow 0 & \quad \\ \delta y\rightarrow 0 & \quad \end{matrix}....(1)

जहां\left( { x }_{ i },{ y }_{ i } \right) ,i वे आयत में एक स्वेच्छ बिन्दु (arbitrary point) है तथा सभी पूर्ण आयतों का योगफल लिया जाता है,सीमा ज्ञात करने के लिए आयतों के क्षेत्रफलों का योगफल किसी भी क्रम में लिया जा सकता है।हम पहले एक उर्ध्वाधर पट्टी (vertical strip) में एक के ऊपर एक बने आयतों का योगफल ज्ञात करते हैं, इसके बाद क्षेत्र A में पहली से अन्तिम पट्टी तक सभी पट्टियों का योगफल ज्ञात करते हैं। अतः योगफल (1) निम्न प्रकार लिखा जा सकता है।

How to solve double integrals?

\begin{matrix} lim & n \\ \delta x\rightarrow 0 & \sum { \quad } \quad \\ \delta y\rightarrow 0 & i=1\quad \end{matrix}\begin{matrix} m \\ \sum { \quad } \\ r=1 \end{matrix}f\left( { x }_{ i },{ y }_{ r } \right) \delta x\delta y....(2)

जहां\left( { x }_{ i },{ y }_{ r } \right) ,i वीं उर्ध्वाधर पट्टी के r वें आयत का एक बिन्दु है।i वीं पट्टी में कुल आयतों की संख्या m है तथा n कुल पट्टियां हैं। पहले कोष्ठक के अन्दर का योगफल ज्ञात किया जाता है।यह योग ज्ञात करते समय { x }_{ i } को अचर (constant) मान लिया जाता है।
(2) में कोष्ठक के अन्दर के योग की सीमा लेने पर

\begin{matrix} lim \\ \delta y\rightarrow 0 \end{matrix}\begin{matrix} m \\ \sum { \quad } \\ r=1 \end{matrix}f\left( { x }_{ i },{ y }_{ i } \right) \delta y=\int _{ { y }_{ 1 } }^{ { y }_{ 2 } }{ f\left( x,y \right) } dy....(3)

जहां { y }_{ 1 } व { y }_{ 2 } ,i वीं उर्ध्वाधर पट्टी में y के चरम (extreme) मान है। चूंकि क्षेत्र A नीचे तथा ऊपर क्रमशः वक्र y={ f }_{ 1 }\left( x \right) तथा y={ f }_{ 2 }\left( x \right) से घिरा हुआ है। अतः हम { y }_{ 1 }={ f }_{ 1 }\left( { x }_{ i } \right)
तथा { y }_{ 2 }={ f }_{ 2 }\left( { x }_{ i } \right) ले सकते हैं। अतः (3) को अग्र प्रकार से लिखा जा सकता है:

\begin{matrix} lim \\ \delta x\rightarrow 0 \end{matrix}\begin{matrix} m \\ \sum { \quad } \\ r=1 \end{matrix}f\left( { x }_{ i },{ y }_{ i } \right) \delta y=\int _{ { f }_{ 1 }\left( { x }_{ i } \right) }^{ { f }_{ 2 }\left( { x }_{ i } \right) }{ f\left( { x }_{ i },y \right) } dy\\ =F\left( { x }_{ i } \right) (मान लो)……(4)
तब (2) हो जाता है।

\begin{matrix} lim & n \\ \delta x\rightarrow 0 & \sum { \quad } \quad \\ \delta y\rightarrow 0 & i=1\quad \end{matrix}\begin{matrix} m \\ \sum { \quad } \\ r=1 \end{matrix}f\left( { x }_{ i },{ y }_{ r } \right) \delta y\delta x=\begin{matrix} lim \\ \delta x\rightarrow 0 \end{matrix}\begin{matrix} n \\ \sum { \quad } \\ i=1 \end{matrix}F\left( { x }_{ i } \right) \delta x\\ =\int _{ a }^{ b }{ F\left( x \right) dx } \\ =\int _{ a }^{ b }{ \int _{ { f }_{ 1 }\left( x \right) }^{ { f }_{ 2 }\left( x \right) }{ f\left( x,y \right) } } dydx....(5)
सामान्यतः (6) के दाहिने पक्ष के समाकल में कोष्ठकों का प्रयोग नहीं किया जाता है। अतः इसे निम्न प्रकार से भी लिख सकते हैं;

\int _{ a }^{ b }{ \int _{ { f }_{ 1 }\left( x \right) }^{ { f }_{ 2 }\left( x \right) }{ f\left( x,y \right) } } dxdy
या \int _{ a }^{ b }{ dx } \int _{ { f }_{ 1 }\left( x \right) }^{ { f }_{ 2 }\left( x \right) }{ f\left( x,y \right) } dy

3.द्वि-समाकल को हल करने के लिए (to solve double integrals) कुछ उदाहरण-

निम्नलिखित द्वि-समाकलों के मान ज्ञात कीजिए-
Example-1. \int _{ 0 }^{ 1 }{ \int _{ y }^{ \sqrt { y } }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) } } dydx
Solution-\int _{ 0 }^{ 1 }{ \int _{ y }^{ \sqrt { y } }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) } } dydx\\ =\int _{ 0 }^{ 1 }{ \int _{ y }^{ \sqrt { y } }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) } } dxdy\\ =\int _{ 0 }^{ 1 }{ { \left[ \frac { { x }^{ 3 } }{ 3 } +x{ y }^{ 2 } \right] }_{ y }^{ \sqrt { y } } } dy\\ =\int _{ 0 }^{ 1 }{ \left[ \frac { { y }^{ \frac { 3 }{ 2 } } }{ 3 } +{ y }^{ \frac { 5 }{ 2 } }-\frac { { y }^{ 3 } }{ 3 } -{ y }^{ 3 } \right] dy } \\ =\int _{ 0 }^{ 1 }{ \left[ \frac { { y }^{ \frac { 3 }{ 2 } } }{ 3 } +{ y }^{ \frac { 5 }{ 2 } }-\frac { 4{ y }^{ 3 } }{ 3 } \right] dy } \\ ={ \left[ \frac { 2 }{ 15 } { y }^{ \frac { 5 }{ 2 } }+\frac { 2 }{ 7 } { y }^{ \frac { 7 }{ 2 } }-\frac { 1 }{ 3 } { y }^{ 4 } \right] }_{ 0 }^{ 1 }\\ =\frac { 2 }{ 15 } +\frac { 2 }{ 7 } -\frac { 1 }{ 3 } \\ =\frac { 9 }{ 105 } \\ =\frac { 3 }{ 35 }
Example-2.\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ \left( { x }^{ 2 }y \right) } } dxdy
Solution-\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ \left( { x }^{ 2 }y \right) } } dxdy\\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ \left( { x }^{ 2 }y \right) } } dydx\\ =\int _{ 0 }^{ a }{ { \left[ \frac { { x }^{ 2 }{ y }^{ 2 } }{ 2 } \right] }_{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } } } dx\\ =\int _{ 0 }^{ a }{ \frac { { x }^{ 2 } }{ 2 } \left( { a }^{ 2 }-{ x }^{ 2 } \right) } dx\\ =\frac { 1 }{ 2 } \int _{ 0 }^{ a }{ \left( { a }^{ 2 }{ x }^{ 2 }-{ x }^{ 4 } \right) } dx\\ =\frac { 1 }{ 2 } { \left[ \frac { { a }^{ 2 }{ x }^{ 3 } }{ 3 } -\frac { { x }^{ 5 } }{ 5 } \right] }_{ 0 }^{ a }\\ =\frac { 1 }{ 2 } \left( \frac { { a }^{ 5 } }{ 3 } -\frac { { a }^{ 5 } }{ 5 } \right) \\ =\frac { { a }^{ 5 } }{ 15 }

Example-3.\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ x } } dxdy

Solution–\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ x } } dxdy\\ =\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ x } } dydx\\ =\int _{ 0 }^{ 2 }{ { \left[ xy \right] }_{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } } } dx\\ =\int _{ 0 }^{ 2 }{ x\sqrt { 2x-{ x }^{ 2 } } dx }

put \\ x=2\sin ^{ 2 }{ \theta } \Rightarrow dx=4sin\theta cos\theta

When x=0 then\theta =0

When x=2 then\theta =\frac { \pi }{ 2 }

I==\int _{ 0 }^{ \frac { \pi }{ 2 } }{ 2\sin ^{ 2 }{ \theta } } \sqrt { 4\sin ^{ 2 }{ \theta } -4\sin ^{ 4 }{ \theta } } 4\sin { \theta } \cos { \theta } d\theta \\ =8\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \sin ^{ 3 }{ \theta } } \cos { \theta . } 2\sin { \theta } \sqrt { 1-\sin ^{ 2 }{ \theta } } d\theta \\ =16\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \sin ^{ 4 }{ \theta } \cos ^{ 2 }{ \theta } } d\theta \\ =16\frac { \left( \frac { 4+1 }{ 2 } \right) !\left( \frac { 2+1 }{ 2 } \right) ! }{ 2\left( \frac { 4+2+2 }{ 2 } \right) ! } \\ =16\frac { \left( \frac { 5 }{ 2 } \right) !\left( \frac { 3 }{ 2 } \right) ! }{ 2\left( 4 \right) ! } \\ =16\frac { \frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } .\frac { 1 }{ 2 } \sqrt { \pi } }{ 2\times 3! } \\ =\frac { 3\pi }{ 3\times 2 } \\ =\frac { \pi }{ 2 }

How to solve double integrals?

Example-4.\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-y^{ 2 } } }{ \sqrt { { a }^{ 2 }-{ x }^{ 2 }-y^{ 2 } } } } dydx
Solution-\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-y^{ 2 } } }{ \sqrt { { a }^{ 2 }-{ x }^{ 2 }-y^{ 2 } } } } dydx\\ =\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-y^{ 2 } } }{ \sqrt { { \left( \sqrt { { a }^{ 2 }-y^{ 2 } } \right) }^{ 2 }-{ x }^{ 2 } } } } dxdy\\ =\int _{ 0 }^{ a }{ { \left[ \frac { x }{ 2 } \sqrt { { a }^{ 2 }-{ y }^{ 2 }-x^{ 2 } } +\frac { \left( { a }^{ 2 }-{ y }^{ 2 } \right) }{ 2 } \sin ^{ -1 }{ \frac { x }{ \sqrt { { a }^{ 2 }-y^{ 2 } } } } \right] }_{ 0 }^{ \sqrt { { a }^{ 2 }-y^{ 2 } } } } dy\\ =\int _{ 0 }^{ a }{ \frac { \left( { a }^{ 2 }-{ y }^{ 2 } \right) }{ 2 } \sin ^{ -1 }{ \frac { \sqrt { { a }^{ 2 }-y^{ 2 } } }{ \sqrt { { a }^{ 2 }-y^{ 2 } } } } } dy\\ =\frac { 1 }{ 2 } \int _{ 0 }^{ a }{ \left( { a }^{ 2 }-{ y }^{ 2 } \right) \sin ^{ -1 }{ \left( 1 \right) } } dy\\ =\frac { \pi }{ 4 } { \left[ a^{ 2 }y-\frac { { y }^{ 3 } }{ 3 } \right] }_{ 0 }^{ a }\\ =\frac { \pi }{ 4 } \left[ { a }^{ 3 }-\frac { { a }^{ 3 } }{ 3 } \right] \\ =\frac { \pi { a }^{ 3 } }{ 6 }

Example-5.दीर्घवृत्त \frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1 द्वारा घिरे हुए क्षेत्र \iint _{ R }^{ \quad }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) dxdy } का मान ज्ञात कीजिए।
(Evaluate \iint _{ R }^{ \quad }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) dxdy } over the region bounded by the ellipse\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1)
Solution-दीर्घवृत्त के समीकरण से-

y=\pm b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } }

समाकलन निम्न वक्रों द्वारा घिरा हुआ है

y=+b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } } ,y=-b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } }
x=-a,x=a
अतः\iint _{ R }^{ \quad }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) dxdy } \\ =\int _{ -a }^{ a }{ \int _{ -b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } } }^{ +b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } } }{ \left( { x }^{ 2 }+{ y }^{ 2 } \right) dydx } } \\ =2\int _{ -a }^{ a }{ { \left[ { x }^{ 2 }y+\frac { 1 }{ 3 } { y }^{ 3 } \right] }_{ 0 }^{ b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } } }dx } \\ =2\int _{ -a }^{ a }{ { \left[ { x }^{ 2 }b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } } +\frac { 1 }{ 3 } { b }^{ 3 }{ \left( 1-\frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) }^{ \frac { 3 }{ 2 } } \right] }dx } \\ =4\int _{ 0 }^{ a }{ { x }^{ 2 }b\sqrt { 1-{ \left( \frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) } } +\frac { 1 }{ 3 } { b }^{ 3 }{ \left( 1-\frac { { x }^{ 2 } }{ { a }^{ 2 } } \right) }^{ \frac { 3 }{ 2 } }dx }

put x=a\sin { \theta } \Rightarrow dx=a\cos { \theta d\theta }
When x=0,\theta =0 and 

When x=a,\theta =\frac { \pi }{ 2 }

=4ab\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \left( { a }^{ 2 }\sin ^{ 2 }{ \theta \cos { \theta } +\frac { 1 }{ 3 } { b }^{ 2 }\cos ^{ 3 }{ \theta } } \right) } cos\theta d\theta \\ =4ab\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \left( { a }^{ 2 }\sin ^{ 2 }{ \theta \cos ^{ 2 }{ \theta } +\frac { 1 }{ 3 } { b }^{ 2 }\cos ^{ 4 }{ \theta } } \right) d\theta } \\ =4ab\left[ \frac { { a }^{ 2 }\left( \frac { 3 }{ 2 } \right) !.\left( \frac { 3 }{ 2 } \right) ! }{ 2.3! } +\frac { 1 }{ 3 } { b }^{ 2 }\frac { \left( \frac { 1 }{ 2 } \right) !.\left( \frac { 5 }{ 2 } \right) ! }{ 2.3! } \right] \\ =4ab\left[ \frac { { a }^{ 2 }\frac { 1 }{ 2 } \left( \pi \right) !.\frac { 1 }{ 2 } \left( \pi \right) ! }{ 2.2.1 } +\frac { 1 }{ 3 } { b }^{ 2 }\frac { \frac { 1 }{ 2 } \left( \pi \right) !\frac { 3 }{ 2 } \left( \pi \right) ! }{ 2.2.1 } \right] \\ =4ab\left[ \frac { 1 }{ 16 } \pi { a }^{ 2 }+\frac { 1 }{ 16 } \pi { b }^{ 2 } \right] \\ =\frac { ab }{ 4 } \left( { a }^{ 2 }+{ b }^{ 2 } \right)

उपर्युक्त उदाहरणों के द्वारा द्वि-समाकल को हल करने (to solve double integrals) को समझा जा सकता है।

4.एक द्विसमाकल आपको क्या देता है?(what does a double integrals give you?)-

एक द्वि-समाकल से हम किसी भी आयताकार या अन्य ठोस आकृतियों का क्षेत्रफल ज्ञात कर सकते हैं। इसलिए द्वि-समाकल का प्रयोग आयताकार समतल आकृतियों का क्षेत्रफल अथवा ठोसों का क्षेत्रफल ज्ञात करने में किया जा सकता है।

5.क्या तुम दो समाकल को गुणा कर सकते हो?(Can you multiply 2 integrals?)-

दो समाकलों का गुणनफल का तात्पर्य है कि यदि दो फलनों का गुणनफल दिया हुआ हो तो उनका समाकल कैसे ज्ञात किया जाए?इसके लिए समाकलन गणित में दोनों फलनों के गुणनफल का समाकल ज्ञात करने हेतु खण्डश: समाकलन के सूत्र का उपयोग किया जाता है।

उपर्युक्त सवालों के उत्तर द्वारा ओर ठीक प्रकार से द्वि-समाकल को हल करने (to solve double integrals) को समझा जा सकता है।

Also Read This Article:-Radius of curvature for polar equation

Satyam Mathematics

About my self
Lekhak Ke Baare Mein (About the Author)
**Satyam Narain Kumawat**
**Website Name:Satyam Mathematics**
*Owner:satyamcoachingcentre.in*
*Sthan:Manoharpur,Jaipur (Rajasthan)*
**Teaching Mathematics aur Anya Anubhav**
***Shiksha:**B.sc.,B.Ed.,(M.sc. star Ke Mathematics Ko Padhane ka Anubhav),B.com.,M.com. Ke vishayon Ko Padhane ka Anubhav,Philosophy,Psychology,Religious,sanskriti Mein Gahri Ruchi aur Adhyayan
***Anubhav:**phichale 23 varshon se M.sc.,M.com.,Angreji aur Vigyan Vishayon Mein Shikshaka Ka Lamba Anubhav
***Visheshagyata:*Maths,Adhyatma (spiritual),Yog vishayon ka vistrit Gyan*
****In Brief:I have read about M.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 23 years teaching experience upto M.sc. ,M.com.,English and science.