Complex Line Integral
1.सम्मिश्र रेखा समाकल (Complex Line Integral)-
सम्मिश्र रेखा समाकल (Complex Line Integral) में समाकल की रीमान परिभाषा तथा वास्तविक रेखा समाकल का अध्ययन करेंगे।
(1.)समाकलन की रीमान परिभाषा (Riemann Definition of Integration)-
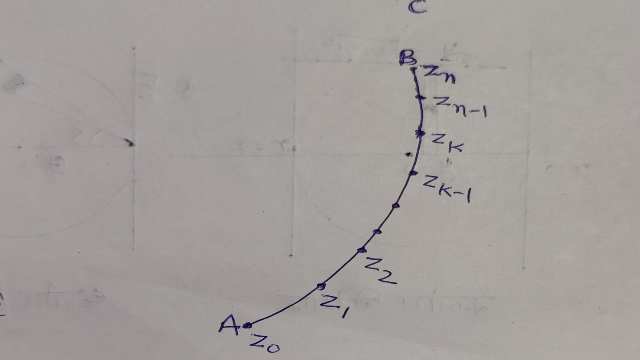
माना कि f(z) सम्मिश्र चर z का संतत फलन है जिसका विश्लेषिक होना आवश्यक नहीं है परन्तु चापकलनीय चाप C (जिसके सिरे बिन्दु A तथा B हैं) के प्रत्येक बिन्दु के संगत f(z) का एक निश्चित मान है।
माना कि चाप C का समीकरण
z=x\left( t \right) +iy\left( t \right) ,\alpha \le t\le \beta है।
माना कि अन्तराल \left[ \alpha ,\beta \right] का
p=\left\{ \alpha ={ t }_{ 0 },{ t }_{ 1 },{ t }_{ 2 },...........,{ t }_{ n }=\beta \right\}
कोई स्वेच्छ विभाजन है तथा t के इन मानों के संगत z के मान हैं।
\left\{ a={ z }_{ 0 },{ z }_{ 1 },{ z }_{ 2 },..........,{ z }_{ n }=b \right\}
योग \overset { n }{ \underset { k=1 }{ \Sigma } } f\left( { \xi }_{ k } \right) \left( { z }_{ k }-{ z }_{ k-1 } \right)
(जहां { \xi }_{ k } चाप { z }_{ k-1 }{ z }_{ k } में कोई बिन्दु है) बनाओ।
अब यदि प्रत्येक चयनित बिन्दु { \xi }_{ k } तथा प्रत्येक विभाजन P के लिए इस योग की सीमा अद्वितीय राशि I हो जबकि n\rightarrow \infty एवं max\left( \left| { t }_{ 1 }-{ t }_{ 0 } \right| ,\left| { t }_{ 2 }-{ t }_{ 1 } \right| ,........,\left| { t }_{ n }-{ t }_{ n-1 } \right| \right)
अर्थात् \left\| p \right\| \rightarrow 0 तब फलन f(z) चाप C के अनुदिश a से b तक समाकलनीय (Integrable) होगा तथा इसे हम निम्न प्रकार लिख सकते हैं।
I={ \int }_{ C }f\left( z \right) dz...............(1)
यहां यह बात ध्यान देने योग्य है कि C पर f(z) की सांतत्यता समाकलन (1) के अस्तित्वता की पर्याप्त प्रतिबन्ध है। अतः
{ \int }_{ C }f\left( z \right) dz=\left\| p \right\| \rightarrow 0\lim _{ n\rightarrow \infty }{ \overset { n }{ \underset { r=1 }{ \Sigma } } f\left( { \xi }_{ r } \right) \left( { z }_{ r }-{ z }_{ r-1 } \right) }
जहां { z }_{ r-1 }\le { \xi }_{ r }\le { z }_{ r }
{ \int }_{ C }f\left( z \right) dz को सम्मिश्र रेखा समाकल या f(z) का C के अनुदिश रेखा समाकल या C के अनुदिश a से b तक f(z) का निश्चित समाकल कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Weiertrass M-test in Complex Analysis
(2.)वास्तविक रेखा समाकल (Real Line Integral)-
माना कि P(x,y) एवं Q(x,y) वास्तविक फलन है जो कि C के प्रत्येक बिन्दु पर संतत है तो वक्र C के अनुदिश वास्तविक रेखा Pdx+Qdy को
{ \int }_{ C }\left[ P\left( x,y \right) dx+Q\left( x,y \right) dy \right]
या { \int }_{ C }Pdx+Qdy...............(3)
संकेत से व्यक्त करते हैं।
यदि वक्र C का प्राचलिक समीकरण x=f(t) तथा y=g(t) ,{ t }_{ 1 }\le t\le { t }_{ 2 } हो तो समाकल (3) को निम्न प्रकार से लिखा जा सकता है:
\int _{ { t }_{ 1 } }^{ { t }_{ 2 } }{ \left[ P\left\{ f\left( t \right) ,g\left( t \right) \right\} { f }^{ ' }\left( t \right) dt+Q\left\{ f\left( t \right) ,g\left( t \right) \right\} { g }^{ ' }\left( t \right) dt \right] } ............(4)
पुनः यदि f(z)=u(x,y)+iv(x,y)=u+iv
जहां z=x+iy,तो सम्मिश्र रेखा समाकल { \int }_{ C }f\left( z \right) dz को वास्तविक रेखा समाकल के रूप में निम्न प्रकार से व्यक्त किया जा सकता है:
{ \int }_{ C }f\left( z \right) dz={ \int }_{ C }\left( u+iv \right) \left( dx+idy \right) \\ ={ \int }_{ C }\left( udx-vdy \right) +i{ \int }_{ C }\left( vdx+udy \right) ............\left( 5 \right)
(3.)सम्मिश्र समाकल का मापांक (Absolute of a complex Integral)-
प्रमेय (Theorem)-यदि l लम्बाई वाले कंटूर C पर फलन f(z) संतत हो तथा
\left| f\left( z \right) \right| \le M\forall z\epsilon c,तो
(If f(z) is continuous on a contour C of length l and katex]\left| f\left( z \right) \right| \le M\forall z\epsilon c[/katex] for every point z on C,then)
\left| { \int }_{ C }f\left( z \right) dz \right| \le Ml
उपपत्ति (Proof):हम जानते हैं कि
{ \int }_{ C }f\left( z \right) dz=\lim _{ n\rightarrow \infty }{ \overset { n }{ \underset { r=1 }{ \Sigma } } f\left( { \xi }_{ r } \right) \left( { z }_{ r }-{ z }_{ r-1 } \right) }
जहां { \xi }_{ r } चाप { z }_{ r-1 }\quad { z }_{ r }पर कोई बिन्दु है।
अब \left| { \overset { n }{ \underset { r=1 }{ \Sigma } } f\left( { \xi }_{ r } \right) \left( { z }_{ r }-{ z }_{ r-1 } \right) } \right| \le \overset { n }{ \underset { r=1 }{ \Sigma } } \left| f\left( { \xi }_{ r } \right) \right| \left| \left( { z }_{ r }-{ z }_{ r-1 } \right) \right| \le M\overset { n }{ \underset { r=1 }{ \Sigma } } \left| \left( { z }_{ r }-{ z }_{ r-1 } \right) \right| \\ \left[ \because \left| f\left( z \right) \right| \le M\forall z\epsilon c \right] \\ \therefore \left| { \int }_{ C }f\left( z \right) dz \right| \le M\lim _{ n\rightarrow \infty }{ \overset { n }{ \underset { r=1 }{ \Sigma } } \left| \left( { z }_{ r }-{ z }_{ r-1 } \right) \right| } \\ \therefore \left| { \int }_{ C }f\left( z \right) dz \right| \le Ml
क्योंकि\left| \left( { z }_{ r }-{ z }_{ r-1 } \right) \right| =l (कंटूर की लम्बाई)
2.सम्मिश्र रेखा समाकल समस्याओं के हल (Complex Line Integral Solved Problems),सम्मिश्र समाकलन समस्याएं हल सहित (Complex integration solved problems),रेखा समाकल उदाहरण (line integral example)-
निम्न वक्र के अनुदिश समाकल का मान ज्ञात कीजिए।
(Evaluate the integral along the following curves:)
Example-1.\int _{ \left( 0,3 \right) }^{ \left( 2,4 \right) }{ \left( 2y+{ x }^{ 2 } \right) dx+\left( 3x-y \right) dy }
सरल रेखा (0,3) से (2,3) तक तत्पश्चात (2,3) से (2,4) तक।(Straight line from (0,3) to (2,3) and then (2,3) to (2,4))
Solution-\int _{ \left( 0,3 \right) }^{ \left( 2,4 \right) }{ \left( 2y+{ x }^{ 2 } \right) dx+\left( 3x-y \right) dy }
बिन्दु (0,3) से (2,3) तक गुजरने वाली रेखा का समीकरण
y-{ y }_{ 1 }=\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } (x-{ x }_{ 1 })\\ y-3=\frac { 3-2 }{ 2-0 } \left( x-0 \right) \\ \Rightarrow y=3\\ dy=0\\ \int _{ 0 }^{ 2 }{ \left( 2\left( 3 \right) +{ x }^{ 2 } \right) dx+\left( 3x-3 \right) \left( 0 \right) } \\ \Rightarrow \int _{ 0 }^{ 2 }{ \left( 6+{ x }^{ 2 } \right) dx } \\ \Rightarrow { \left[ 6x+\frac { { x }^{ 3 } }{ 3 } \right] }_{ 0 }^{ 2 }\\ \\ \Rightarrow \left[ 6x+\frac { { 2 }^{ 3 } }{ 3 } \right] \\ \Rightarrow 12+\frac { 8 }{ 3 } \\ \Rightarrow \frac { 44 }{ 3 } .....(1)
बिन्दु (2,3) से (2,4) तक गुजरने वाली रेखा का समीकरण
y-3=\frac { 4-3 }{ 2-2 } \left( x-2 \right) \\ \Rightarrow x=2\\ dx=0\\ \int _{ 3 }^{ 4 }{ \left( 2y+{ 2 }^{ 2 } \right) \left( 0 \right) +\left( 3\times 2-y \right) dy } \\ \Rightarrow \int _{ 3 }^{ 4 }{ \left( 6-y \right) dy } \\ \Rightarrow { \left[ 6y-\frac { { y }^{ 2 } }{ 2 } \right] }_{ 3 }^{ 4 }\\ \Rightarrow \left[ 6\times 4-\frac { { 4 }^{ 2 } }{ 2 } -6\times 3+\frac { { 3 }^{ 2 } }{ 2 } \right] \\ \Rightarrow [24-8-18+\frac { 9 }{ 2 } ]\\ \Rightarrow [-2+\frac { 9 }{ 2 } ]\\ \Rightarrow [\frac { -4+9 }{ 2 } ]\\ \Rightarrow \frac { 5 }{ 2 } ..........(2)
(1) व (2) का योग करने पर-
=\frac { 44 }{ 3 } +\frac { 5 }{ 2 } \\ =\frac { 88+15 }{ 6 } \\ =\frac { 103 }{ 6 }
Example-2.यदि C,y={ x }^{ 3 }-3{ x }^{ 2 }+4x-1 पर स्थित बिन्दुओं (1,1) तथा (2,3) को मिलाने वाला वक्र हो तो समाकल { \int }_{ C }\left( 12{ z }^{ 2 }-4iz \right) dz का मान ज्ञात करो
(If C is the curve y={ x }^{ 3 }-3{ x }^{ 2 }+4x-1 joining the points (1,1) and (2,3),find the value of { \int }_{ C }\left( 12{ z }^{ 2 }-4iz \right) dz)
Solution-{ \int }_{ C }\left( 12{ z }^{ 2 }-4iz \right) dz\\ z=x+iy\Rightarrow dz=dx+idy\\ { \int }_{ C }\left[ 12{ \left( x+iy \right) }^{ 2 }-4i\left( x+iy \right) \right] \left( dx+idy \right) \\ y={ x }^{ 3 }-3{ x }^{ 2 }+4x-1\\ dy=\left( 3{ x }^{ 2 }-6x+4 \right) dx
अतः\int _{ 1 }^{ 2 }{ [12{ \left\{ x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) \right\} }^{ 2 } } -4i\left\{ x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) \right\} ][dx+i\left( 3{ x }^{ 2 }-6x+4 \right) dx]\\ \Rightarrow \int _{ 1 }^{ 2 }{ [12{ \left\{ x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) \right\} }^{ 2 } } -4i\left\{ x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) \right\} ][1+i\left( 3{ x }^{ 2 }-6x+4 \right) ]dx\\ put\quad x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) =t\\ \left[ 1+i\left( 3{ x }^{ 2 }-6x+4 \right) \right] dx=dt\\ { \int }_{ 1 }^{ 2 }\left[ 12{ t }^{ 2 }-4it \right] dt\\ \Rightarrow { \left[ 4{ t }^{ 3 }-2i{ t }^{ 2 } \right] }_{ 1 }^{ 2 }\\ \Rightarrow { \left[ \begin{matrix} 4{ \left\{ x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) \right\} }^{ 3 } \\ -2i{ \left\{ x+i\left( { x }^{ 3 }-3{ x }^{ 2 }+4x-1 \right) \right\} }^{ 2 } \end{matrix} \right] }_{ 1 }^{ 2 }\\ \Rightarrow [4{ \left\{ 2+i\left( { 2 }^{ 3 }-3\times { 2 }^{ 2 }+4\times 2-1 \right) \right\} }^{ 3 }-2i{ \left\{ 2+i\left( { 2 }^{ 3 }-3\times { 2 }^{ 2 }+4\times 2-1 \right) \right\} }^{ 2 }-4{ \left\{ 1+i\left( { 1 }^{ 3 }-3\times { 1 }^{ 2 }+4\times 1-1 \right) \right\} }^{ 3 }+2i{ \left\{ 1+i\left( { 1 }^{ 3 }-3\times { 1 }^{ 2 }+4\times 1-1 \right) \right\} }^{ 2 }]\\ \Rightarrow [4{ \left( 2+3i \right) }^{ 3 }-2i{ \left( 2+3i \right) }^{ 2 }-4{ \left\{ 1+i\left( 1 \right) \right\} }^{ 3 }+2i{ \left\{ 1+i\left( 1 \right) \right\} }^{ 2 }]\\ \Rightarrow { \left[ 4{ \left( 2+3i \right) }^{ 3 }-2i{ \left( 2+3i \right) }^{ 2 }-4{ \left( 1+i \right) }^{ 3 }+2i{ \left( 1+i \right) }^{ 2 } \right] }\\ \Rightarrow 4\left( 8-27i+36i-54 \right) -2i\left( 4-9+12i \right) -4{ \left( 1+i \right) }^{ 3 }+2i{ \left( 1+i \right) }^{ 2 }\\ \Rightarrow 4\left( -46+9i \right) -2i\left( -5+12i \right) -4\left( 1-i+3i-3 \right) +2i\left( 1-1+2i \right) \\ \Rightarrow -184+36i+10i+24-4\left( -2+2i \right) +2i\left( 2i \right) \\ \Rightarrow -160+46i+8-8i-4\\ \Rightarrow -156+38i
Example-3.मान ज्ञात कीजिए (Evaluate)
{ \int }_{ C }\left( x+2y \right) dx+\left( y-2x \right) dy
जहां C दीर्घवृत्त x=4\cos { \theta } ,y=3\sin { \theta } ,0\le \theta \le 2\pi से परिभाषित वामावर्त दिशा में है।
(Where C is defined by the ellipse x=4\cos { \theta } ,y=3\sin { \theta } ,0\le \theta \le 2\pi and is in anticlockwise direction.)
Solution-{ \int }_{ C }\left( x+2y \right) dx+\left( y-2x \right) dy\\ x=4\cos { \theta } ,y=3\sin { \theta } \\ dx=-4\sin { \theta } d\theta ,dy=3\cos { \theta } d\theta \\ { \int }_{ 0 }^{ 2\pi }[\left( 4\cos { \theta } +6\sin { \theta } \right) \left( -4\sin { \theta } d\theta \right) +\left( 3\sin { \theta } -8\cos { \theta } \right) \left( 3\cos { \theta } d\theta \right) ]\\ \Rightarrow { \int }_{ 0 }^{ 2\pi }(-16\sin { \theta } \cos { \theta } -24\sin ^{ 2 }{ \theta } +9\sin { \theta } \cos { \theta } -24\cos ^{ 2 }{ \theta } )d\theta \\ \Rightarrow { \int }_{ 0 }^{ 2\pi }(-7\sin { \theta } \cos { \theta } -24)d\theta \\ \Rightarrow { \int }_{ 0 }^{ 2\pi }(-\frac { 7 }{ 2 } \sin { 2\theta } -24)d\theta \\ \Rightarrow { [\frac { 7 }{ 4 } \cos { 2\theta } -24\theta ] }_{ 0 }^{ 2\pi }\\ \Rightarrow \frac { 7 }{ 4 } \cos { 4\pi } -24(2\pi )-\frac { 7 }{ 4 } \cos { 0 } \\ \Rightarrow \frac { 7 }{ 4 } -48\pi -\frac { 7 }{ 4 } \\ \Rightarrow -48\pi
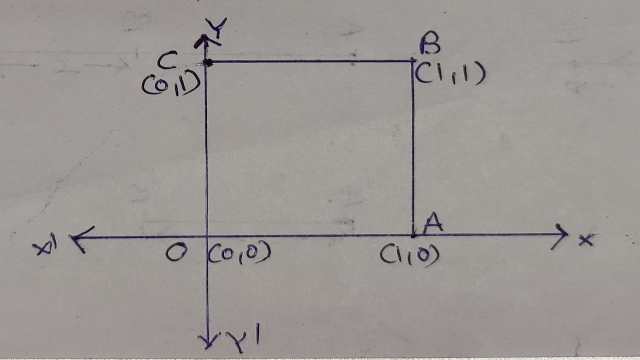
Example-4. \int _{ c }^{ \quad }{ { \left| z \right| }^{ 2 } } dz का मान वर्ग जिसके शीर्ष (0,0),(1,0),(1,1),(0,1) हैं,के अनुदिश ज्ञात कीजिए।
(Evaluate \int _{ c }^{ \quad }{ { \left| z \right| }^{ 2 } } dz around the square with vertices at (0,0),(1,0),(1,1),(0,1).)
Solution-
चित्र के अनुसार
\int _{ c }^{ \quad }{ { \left| z \right| }^{ 2 } } dz=\int _{ OABO }^{ \quad }{ { \left| z \right| }^{ 2 }dz } \\ =\int _{ OA }^{ \quad }{ { \left| z \right| }^{ 2 }dz } +\int _{ AB }^{ \quad }{ { \left| z \right| }^{ 2 }dz } +\int _{ BC }^{ \quad }{ { \left| z \right| }^{ 2 }dz } +\int _{ CO }^{ \quad }{ { \left| z \right| }^{ 2 }dz }
अब OA पर,y=0,dy=0 तथा x का मान 0 से 1 तक होगा।
AB पर x=1,dx=0 तथा y का मान 0 से 1तक होगा।
BC पर y=1,dy=0 तथा x का मान 1 से 0 तक होगा।
CO पर x=0,dx=0 तथा का मान 1 से 0 तक होगा।
z=x+iy तथा dz=dx+idy रखने पर-
\int _{ c }^{ \quad }{ { \left| z \right| }^{ 2 } } dz=\int _{ OA }^{ \quad }{ ({ x }^{ 2 }+{ y }^{ 2 })(dx+idy) } +\int _{ AB }^{ \quad }{ ({ x }^{ 2 }+{ y }^{ 2 })(dx+idy) } +\int _{ BC }^{ \quad }{ ({ x }^{ 2 }+{ y }^{ 2 })(dx+idy) } +\int _{ CO }^{ \quad }{ ({ x }^{ 2 }+{ y }^{ 2 })(dx+idy) } \\ =\int _{ 0 }^{ 1 }{ { x }^{ 2 }dx } +\int _{ 0 }^{ 1 }{ (1+{ y }^{ 2 })idy } +\int _{ 1 }^{ 0 }{ { (x }^{ 2 }+1)dx } +\int _{ 1 }^{ 0 }{ { y }^{ 2 }idy } \\ ={ [\frac { { x }^{ 3 } }{ 3 } ] }_{ 0 }^{ 1 }+i{ [y+\frac { { y }^{ 3 } }{ 3 } ] }_{ 0 }^{ 1 }+{ [\frac { { x }^{ 3 } }{ 3 } +x] }_{ 1 }^{ 0 }+i{ [\frac { { y }^{ 3 } }{ 3 } ] }_{ 1 }^{ 0 }\\ =\frac { 1 }{ 3 } +\frac { 4 }{ 3 } i-\frac { 4 }{ 3 } -\frac { 1 }{ 3 } i\\ =-\frac { 3 }{ 3 } +\frac { 3 }{ 3 } i\\ =(-1+i)
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र रेखा समाकल (Complex Line Integral) को समझ सकते हैं।
3.सम्मिश्र रेखा समाकल की समस्याएं (Complex Line Integral Problems)-
(1.)मान ज्ञात कीजिए (Evaluate)
\int _{ C }^{ \quad }{ { ({ z }^{ 2 }+1) }^{ 2 }dz }
जहां C चक्रज s=a(\theta -\sin { \theta } ),y=a(1-\cos { \theta } ) का \theta =0 से \theta =2\pi तक चाप है।
(Where C is arc of the cycloid s=a(\theta -\sin { \theta } ),y=a(1-\cos { \theta } ) from the point \theta =0 to \theta =2\pi )
(2.)मान ज्ञात कीजिए
\int _{ 0 }^{ 1+i }{ (z-1)dz } परवलय y={ x }^{ 2 } के अनुदिश
(along the parabola y={ x }^{ 2 })
(3.)निम्न वक्र के अनुदिश समाकल का मान ज्ञात कीजिए (Evaluate the integral along the following curves)
\int _{ (0,3) }^{ (2,4) }{ (2y+{ x }^{ 2 })dx+(3x-y)dy }
सरल रेखा (0,3) से (2,4) तक।[a straight line from (0,3) to (2,4)]
(4.)मान ज्ञात कीजिए (Evaluate):
\int _{ C }^{ \quad }{ ({ x }^{ 2 }-i{ y }^{ 2 })dz }
जहां (where)
परवलय y=2x^{ 2 } को बिन्दुओं (1,1) तथा (2,8) को मिलाने वाला वक्र है।(C is a parabola joining the points (1,1) to (2,8).)
Answer-
(1)\frac { 1 }{ 15 } (96{ \pi }^{ 5 }{ a }^{ 5 }+80{ \pi }^{ 3 }{ a }^{ 3 }+30\pi a)\\ (2)-1\\ (3)\frac { 97 }{ 6 } \\ (4)\frac { 511 }{ 3 } -\frac { 49 }{ 5 } i
उपर्युक्त सवालों को हल करने पर सम्मिश्र रेखा समाकल (Complex Line Integral) को ठीक से समझा जा सकता है।
4.सम्मिश्र विश्लेषण रेखा समाकल (Line integral complex analysis)-
यहाँ मूल विषय यह है कि सम्मिश्र लाइन इंटीग्रल्स जो हम देखते हैं,उसमें से अधिकांश को प्रतिबिंबित करेंगे।
बहुचर अवकल रेखा समाकल। लेकिन, { e }^{ i\theta } के साथ काम करने की तरह साइन और कोसाइन के साथ के साथ काम करने से ज्यादा आसान है,सम्मिश्र लाइन इंटीग्रल्स उनके बहु-चर एनालॉग की तुलना में काम करना आसान है।साथ ही वे इन समाकलों के कामकाज की गहरी जानकारी देंगे।
5.रेखा समाकल का क्या अर्थ है? (What does a line integral mean?)-
एक लाइन इंटीग्रल (कभी-कभी एक पथ इंटीग्रल कहा जाता है) एक वक्र के साथ कुछ फ़ंक्शन का समाकल है। एक वक्र के साथ एक स्केलर-मूल्यवान फ़ंक्शन को समाकलन कर सकता है, उदाहरण के लिए,इसके घनत्व से एक तार का द्रव्यमान।एक वक्र के साथ एक निश्चित प्रकार के वेक्टर-मूल्यवाले फलनों को भी समाकल कर सकता है।
6.क्या सम्मिश्र संख्याओं को समाकल कर सकते हैं? (Can complex numbers integrate?)-
यदि आप वास्तविक चर के सम्मिश्र मूल्यवाले फ़ंक्शन का मतलब है,तो आप वास्तविक और काल्पनिक भागों को अलग-अलग समाकलन कर सकते हैं।लेकिन ऐसा करने की कोई जरूरत नहीं हो सकती है।उदाहरण के लिए समाकल वास्तविक फलनों के लिए है।यदि आप एक सम्मिश्र चर के सम्मिश्र फलनों का मतलब है तो आपको एक वक्र के साथ समाकल करना होगा।
7.आप एक सम्मिश्र फलन को पैरामैट्राइज कैसे करते हैं? (How do you parameterize a complex function?)-
(एकल) वास्तविक चर के सम्मिश्र फलन
मान लीजिए कि x (t) और y (t) एक वास्तविक चर t के फलन हैं।सभी बिंदुओं से मिलकर D का सेट
अंक z (t) = x (t) + iy (t) के लिए a ≤ t ≤ b को सम्मिश्र तल में पैरामीट्रिक वक्र या सम्मिश्र पैरामीट्रिक वक्र कहा जाता है। फ़ंक्शन z (t) को पैरामीट्रिक भी कहा जाता है
,तल में वक्र D का।
कॉम्प्लेक्स प्लेन में आम पैरामीट्रिक कर्व्स
लाइन सेगमेंट (z_{ 0 } से z_{ 1 } तक)
z(t)=z_{ 0 }(1-t)+z_{ 1 }t,0\le t<1
रे (क्षैतिज अक्ष पर कोण α पर z_{ 0 } पर है)
z(t)=z_{ 0 }+t{ e }^{ i\alpha },0\le t\le \infty
सर्कल (त्रिज्या r के साथ z_{ 0 } पर केंद्रित)
z(t)=z_{ 0 }+r{ e }^{ it },0\le t\le 2\pi
एक सम्मिश्र मानचित्रण के तहत एक पैरामीट्रिक वक्र की छवि
एक जटिल चर w = f (z) के एक सम्मिश्र फलन और एक सम्मिश्र पैरामीट्रिक वक्र को देखते हुए D, z(t) for a ≤ t ≤ b फ़ंक्शन w(t) = f(z(t)) for a ≤ t ≤ b के लिए प्रतिनिधित्व करता है
जो D का पैराट्राइज़ेशन है।, डी की छवि।
8.सम्मिश्र रेखा समाकल जो पथ से स्वतन्त्र है (The complex line integral is path independent)-
पथ स्वतंत्रता
दूसरे शब्दों में, F समाकल C पर बिंदु R (b) और r (a) पर G के मूल्यों पर ही निर्भर करता है,और इस प्रकार उनके बीच के मार्ग से स्वतंत्र होता है।इस कारण से, एक परम्परागत वेक्टर क्षेत्र का एक समाकल पथ स्वतंत्र कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र रेखा समाकल (Complex Line Integral) की कांसेप्ट क्लीयर हो जाएगी।
Also Read This Article:-Cauchy-Hadamard Theorem
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |









Oh my goodness! an amazing write-up dude. Many thanks Even so My business is experiencing trouble with ur rss . Do not know why Struggle to sign up to it. Can there be everyone getting identical rss dilemma? Anyone who knows kindly respond. Thnkx