Laurent theorem for complex functions
1.सम्मिश्र फलनों के लिए लौरां प्रमेय का परिचय (Introduction to Laurent theorem for complex functions)-
सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions) का अध्ययन करेंगे।कोशी प्रमेय के अनुप्रयोग में कोशी समाकल सूत्र,विश्लेषिक फलनों के अवकलज,मोरेरा प्रमेय (कोशी प्रमेय का विलोम),टेलर प्रमेय एवं लौरां प्रमेय जैसी कई प्रमेयों का अध्ययन किया जाता है।कोशी समाकल सूत्र,विश्लेषिक फलनों के अवकलज,टेलर प्रमेय का अध्ययन हम पूर्व आर्टिकल में कर चुके हैं।इस आर्टिकल में सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions) को सत्यापित करेंगे और इस पर आधारित सवाल भी हल करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Rectilinear Motion in Resisting Medium
2.सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions)-
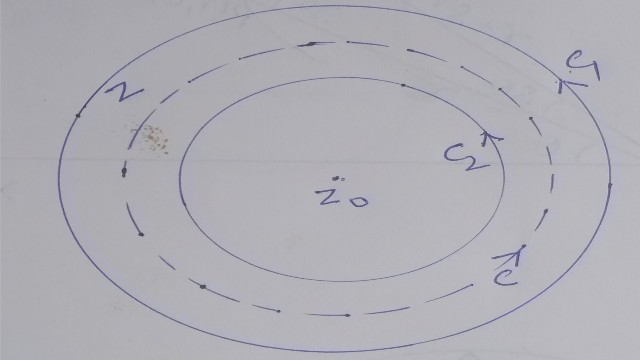
प्रमेय (Theorem)-माना कि दो संकेन्द्रीय वृत्त { c }_{ 1 } एवं { c }_{ 2 } जिनके केन्द्र { z }_{ 0 } तथा त्रिज्याएं { R }_{ 1 } एवं { R }_{ 2 }\left( { R }_{ 1 }>{ R }_{ 2 } \right) के मध्य वलयिका G में f(z) एक विश्लेषिक फलन हो तो वलयिका के किसी बिन्दु z पर
(Let f(z) be analytic in the annulus (ring shaped region) G between two concentric circles { c }_{ 1 } and { c }_{ 2 } With centre{ z }_{ 0 } { R }_{ 1 } and { R }_{ 2 }\left( { R }_{ 1 }>{ R }_{ 2 } \right) radii and respectively then at any point z of the annulus
f\left( z \right) =\sum _{ n=0 }^{ \infty }{ { a }_{ n }{ \left( z-{ z }_{ 0 } \right) }^{ n } } +\sum _{ n=1 }^{ \infty }{ { b }_{ n }{ \left( z-{ z }_{ 0 } \right) }^{ -n } }
उपपत्ति-माना कि वलयाकार क्षेत्र G में z कोई बिन्दु है।तो बहुसम्बन्धित प्रदेश में कोशी समाकल सूत्र से
f\left( z \right) =\frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( w \right) dw }{ w-z } - } \frac { 1 }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ \frac { f\left( w \right) dw }{ w-z } } ....(1)
अब यदि { w\in c }_{ 1 } एवं वलयिका का कोई बिन्दु हो तो निम्न सर्वसमिका (Identity) से-
\frac { 1 }{ w-z } =\frac { 1 }{ \left( w-{ z }_{ 0 } \right) -\left( z-{ z }_{ 0 } \right) } \\ =\frac { 1 }{ \left( w-{ z }_{ 0 } \right) } { \left[ 1-\frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right] }^{ -1 }\\ =\frac { 1 }{ w-{ z }_{ 0 } } { \left[ 1+\left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) +{ \left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) }^{ 2 }+....+{ \left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) }^{ n-1 }+{ \left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) }^{ n }\frac { 1 }{ \left\{ 1-\left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) \right\} } \right] }\\ \left[ \because \left| \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right| <1 \right] \\ =\frac { 1 }{ w-{ z }_{ 0 } } +\frac { \left( z-{ z }_{ 0 } \right) }{ { \left( w-{ z }_{ 0 } \right) }^{ 2 } } +\frac { { \left( z-{ z }_{ 0 } \right) }^{ 2 } }{ { \left( w-{ z }_{ 0 } \right) }^{ 3 } } +.......+\frac { { \left( z-{ z }_{ 0 } \right) }^{ n-1 } }{ { \left( w-{ z }_{ 0 } \right) }^{ n } } +{ \left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) }^{ n }.\frac { 1 }{ w-{ z }_{ 0 } } ......(2)\\ \therefore \frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( w \right) dw }{ w-z } } =\frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( w \right) dw }{ \left( w-{ z }_{ 0 } \right) } } +\frac { z-{ z }_{ 0 } }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( w \right) dw }{ { \left( w-{ z }_{ 0 } \right) }^{ 2 } } } +......+\frac { { \left( z-{ z }_{ 0 } \right) }^{ n-1 } }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( w \right) dw }{ { \left( w-{ z }_{ 0 } \right) }^{ n } } } +{ R }_{ n }\\ { a }_{ 0 }+{ a }_{ 1 }\left( z-{ z }_{ 0 } \right) +{ a }_{ 2 }{ \left( z-{ z }_{ 0 } \right) }^{ 2 }+......+{ a }_{ n-1 }{ \left( z-{ z }_{ 0 } \right) }^{ n-1 }+{ R }_{ n }
जहां { R }_{ n }=\frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ { \left( \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right) }^{ n }\frac { f\left( w \right) dw }{ w-{ z }_{ 0 } } }
एवं { a }_{ n }=\frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( w-{ z }_{ 0 } \right) }^{ n+1 } } } \left( n=0,1,2..... \right) ........(3)
हम प्रदर्शित करेंगे कि { R }_{ n }\rightarrow 0 जबकि n\rightarrow \infty
माना कि \left| z-{ z }_{ 0 } \right| =r ताकि { R }_{ 2 }<r<{ R }_{ 1 }
पुनः \left| { R }_{ n } \right| \le \left| \frac { 1 }{ 2\pi i } \right| \int _{ { c }_{ 1 } }^{ \quad }{ { \left| \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right| }^{ n }\frac { \left| f\left( w \right) \right| \left| dw \right| }{ \left| w-{ z }_{ 0 } \right| } } ....(4)
अब { c }_{ 1 } पर किसी बिन्दु w के लिए
\left| \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right| ={ k }_{ 1 }
जहां { k }_{ 1 }<1 एक अचर संख्या है। एवं
\left| w-z \right| =\left| { \left( w-{ z }_{ 0 } \right) }-\left( z-{ z }_{ 0 } \right) \right| \ge \left| w-{ z }_{ 0 } \right| -\left| z-{ z }_{ 0 } \right| \ge { R }_{ 1 }-r
पुनः माना कि{ M }_{ 1 } एक धनात्मक संख्या इस प्रकार है कि
\left| f\left( w \right) \right| \le { M }_{ 1 }\quad \quad \nvdash w \in { c }_{ 1 }
समीकरण (4) से
\left| { R }_{ n } \right| \le \frac { 1 }{ 2\pi } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { { { K }_{ 1 }^{ n }M }_{ 1 } }{ { R }_{ 1 }-r } } \left| dw \right| \\ \le \frac { 1 }{ 2\pi } \frac { { { K }_{ 1 }^{ n }M }_{ 1 } }{ { R }_{ 1 }-r } .2\pi { R }_{ 1 }\quad \\ \le \quad \frac { { R }_{ 1 }{ M }_{ 1 } }{ { R }_{ 1 }-r } { K }_{ 1 }^{ n }\\ \because { K }_{ 1 }<1\quad \therefore \quad { K }_{ 1 }\rightarrow 0 n\rightarrow \infty
फलत: \lim _{ n\rightarrow \infty }{ { R }_{ n } } =0
अब समीकरण (1) से
\frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( w \right) dw }{ w-z } } =\overset { \infty }{ \underset { n=0 }{ \sum { \quad } } } { a }_{ n }{ \left( z-{ z }_{ 0 } \right) }^{ n }.....(5)
अब समीकरण (1) के द्वितीय समाकल पर विचार करेंगे। समीकरण (2) में z एवं w को परस्पर बदलने पर
\frac { 1 }{ z-w } =-\frac { 1 }{ w-z } =\frac { 1 }{ z-{ z }_{ 0 } } { { \left[ 1-\frac { w-{ z }_{ 0 } }{ z-{ z }_{ 0 } } \right] }^{ -1 } }\\ =\frac { 1 }{ z-{ z }_{ 0 } } +\frac { w-{ z }_{ 0 } }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } +\frac { { \left( w-{ z }_{ 0 } \right) }^{ 2 } }{ { \left( z-{ z }_{ 0 } \right) }^{ 3 } } +.....+\frac { { \left( w-{ z }_{ 0 } \right) }^{ n-1 } }{ { \left( z-{ z }_{ 0 } \right) }^{ n } } +{ \left( \frac { w-{ z }_{ 0 } }{ z-{ z }_{ 0 } } \right) }^{ n }\frac { 1 }{ z-{ z }_{ 0 } }
(द्विपद प्रसार वैद्य है क्योंकि)\left| \frac { w-{ z }_{ 0 } }{ z-{ z }_{ 0 } } \right| =\frac { { R }_{ 2 } }{ r } <1\\ \therefore -\frac { 1 }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ \frac { f\left( w \right) dw }{ w-z } } =\frac { { \left( z-{ z }_{ 0 } \right) }^{ -1 } }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ f\left( w \right) dw } +\frac { { \left( z-{ z }_{ 0 } \right) }^{ -2 } }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ \frac { f\left( w \right) dw }{ { \left( w-{ z }_{ 0 } \right) }^{ -1 } } } +....+\frac { { \left( z-{ z }_{ 0 } \right) }^{ -n } }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ \frac { f\left( w \right) dw }{ { \left( w-{ z }_{ 0 } \right) }^{ -n+1 } } +{ s }_{ n } } \\ ={ b }_{ 1 }{ \left( z-{ z }_{ 0 } \right) }^{ -1 }+{ b }_{ 2 }{ \left( z-{ z }_{ 0 } \right) }^{ -2 }+.......+{ b }_{ n }{ \left( z-{ z }_{ 0 } \right) }^{ -n }+{ s }_{ n }.....(6)
जहां { s }_{ n }=\frac { 1 }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ { \left( \frac { w-{ z }_{ 0 } }{ z-{ z }_{ 0 } } \right) }^{ n }\frac { f\left( w \right) dw }{ z-{ z }_{ 0 } } }
और { b }_{ n }=\frac { 1 }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ \frac { f\left( w \right) dw }{ { \left( w-{ z }_{ 0 } \right) }^{ -n+1 } } } \left( n=1,2,3..... \right) ......(7)
अब प्रत्येक w\in { c }_{ 2 } के लिए हम \left| \frac { w-{ z }_{ 0 } }{ z-{ z }_{ 0 } } \right| ={ k }_{ 2 }<1 ले सकते हैं और
\left| z-w \right| =\left| \left( z-{ z }_{ 0 } \right) -\left( w-{ z }_{ 0 } \right) \right| \ge r-{ R }_{ 2 }
पुनः M एक धनात्मक संख्या इस प्रकार है कि
\left| f\left( w \right) \right| \le { M }_{ 2 }
अतः \left| { s }_{ n } \right| \le \frac { 1 }{ 2\pi } \int _{ { c }_{ 2 } }^{ \quad }{ { \left| \frac { z-{ z }_{ 0 } }{ w-{ z }_{ 0 } } \right| }^{ n }\frac { \left| f\left( w \right) \right| \left| dw \right| }{ \left| z-{ z }_{ 0 } \right| } } \\ \le \frac { 1 }{ 2\pi } \frac { { { k }_{ 2 }^{ n }M }_{ 2 } }{ { r-R }_{ 2 } } .2\pi { R }_{ 2 }\\ \left| { s }_{ n } \right| \le \frac { { { k }_{ 2 }^{ n }M }_{ 2 } }{ { r-R }_{ 2 } } { k }_{ 2 }^{ n }\\ { k }_{ 2 }<1\\ \therefore \lim _{ n\rightarrow \infty }{ { s }_{ n }=0 } ......(8)
अब समीकरण (5) से हमें प्राप्त होता है
-\frac { 1 }{ 2\pi i } \int _{ { c }_{ 2 } }^{ \quad }{ \frac { f\left( w \right) dw }{ w-z } } ={ b }_{ 1 }{ \left( z-{ z }_{ 0 } \right) }^{ -1 }+{ b }_{ 2 }{ \left( z-{ z }_{ 0 } \right) }^{ -2 }+.......+{ b }_{ n }{ \left( z-{ z }_{ 0 } \right) }^{ -n }\\ \overset { \infty }{ \underset { n=0 }{ \sum { \quad } } } { b }_{ n }{ \left( z-{ z }_{ 0 } \right) }^{ -n }
उपर्युक्त से सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions) को समझा जा सकता है।
3.सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions) पर आधारित सवाल-
Question-1.फलन \frac { 1 }{ \left( { z }^{ 2 }+1 \right) \left( z+2 \right) } को निरुपित करनेवाली लौरां श्रेणी प्राप्त कीजिए जहां \left| z \right| >2 एवं 1<\left| z \right| <2
(Find the Laurent series which represents the function \frac { 1 }{ \left( { z }^{ 2 }+1 \right) \left( z+2 \right) } where \left| z \right| >2 and 1<\left| z \right| <2
Solution–\frac { 1 }{ \left( { z }^{ 2 }+1 \right) \left( z+2 \right) } \\ \frac { 1 }{ \left( { z }^{ 2 }+1 \right) \left( z+2 \right) } =\frac { Az+B }{ \left( { z }^{ 2 }+1 \right) } +\frac { C }{ \left( z+2 \right) } \\ \Rightarrow 1=\left( Az+B \right) \left( z+2 \right) +C\left( { z }^{ 2 }+1 \right) \\ \Rightarrow 1=A{ z }^{ 2 }+Bz+2Az+2B+C{ z }^{ 2 }+C\\ \Rightarrow 1=\left( A+C \right) { z }^{ 2 }+\left( B+2A \right) z+2B+C
तुलना करने पर-
A+C=0 ……(1) B+2A=0 …….(3 )
2B+C=1 …….(2)
– – –
…………………………
घटाने पर
A-2B=-1 …..(4)
समीकरण (3) को 2 से गुणा करने पर-
4A+2B=0 ………(5)
A-2B =-1
……………………………..
जोड़ने पर-
5A=-1
A=-\frac { 1 }{ 5 }
(4) में मान रखने पर-
-\frac { 1 }{ 5 } -2B=-1\\ -2B=-1+\frac { 1 }{ 5 } \\ -2B=-\frac { 4 }{ 5 } \\ B=\frac { 2 }{ 5 }
A का मान (1) में रखने पर-
C=\frac { 1 }{ 5 } \\ f\left( z \right) =\frac { -\frac { 1 }{ 5 } z+\frac { 2 }{ 5 } }{ { z }^{ 2 }+1 } +\frac { 1 }{ 5\left( z+2 \right) } \\ f\left( z \right) =-\frac { 1 }{ 5 } \frac { z }{ \left( { z }^{ 2 }+1 \right) } +\frac { 2 }{ 5 } \frac { 1 }{ \left( { z }^{ 2 }+1 \right) } +\frac { 1 }{ 5\left( z+2 \right) }
(i)z>2\\ f\left( z \right) =-\frac { 1 }{ 5 } \frac { z }{ { z }^{ 2 } } { \left( 1+\frac { 1 }{ { z }^{ 2 } } \right) }^{ -1 }+\frac { 2 }{ 5 } \frac { 1 }{ { z }^{ 2 } } { \left( 1+\frac { 1 }{ { z }^{ 2 } } \right) }^{ -1 }+\frac { 1 }{ 5z } { \left( 1+\frac { 2 }{ z } \right) }^{ -1 }\\ f\left( z \right) =-\frac { 1 }{ 5z } \left( 1-\frac { 1 }{ { z }^{ 2 } } +{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 2 }-{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 3 }+.......... \right) +\\ \frac { 2 }{ 5{ z }^{ 2 } } \left( 1-\frac { 1 }{ { z }^{ 2 } } +{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 2 }-{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 3 }+.......... \right) +\\ \frac { 1 }{ 5z } \left( 1-\frac { 2 }{ z } +{ \left( \frac { 2 }{ z } \right) }^{ 2 }-{ \left( \frac { 2 }{ z } \right) }^{ 3 }+....... \right) \\ f\left( z \right) =\frac { 1 }{ 5z } { \left( -1 \right) }^{ n }{ \left( \frac { 2 }{ z } \right) }^{ n }-\frac { 1 }{ 5 } \left[ \frac { 1 }{ z } -\frac { 2 }{ { z }^{ 2 } } \right] \sum _{ n=0 }^{ \infty }{ \frac { { \left( -1 \right) }^{ n } }{ { z }^{ 2n } } }
(ii)1<\left| z \right| <2\\ \frac { 1 }{ \left| z \right| } <1\quad \\ \left| \frac { z }{ 2 } \right| <1\\ f\left( z \right) =-\frac { 1 }{ 5 } \frac { z }{ \left( { z }^{ 2 }+1 \right) } +\frac { 2 }{ 5 } \frac { 1 }{ \left( { z }^{ 2 }+1 \right) } +\frac { 1 }{ 5\left( z+2 \right) } \\ f\left( z \right) =-\frac { 1 }{ 5 } \frac { z }{ { z }^{ 2 } } { \left( 1+\frac { 1 }{ { z }^{ 2 } } \right) }^{ -1 }+\frac { 2 }{ 5 } \frac { 1 }{ { z }^{ 2 } } { \left( 1+\frac { 1 }{ { z }^{ 2 } } \right) }^{ -1 }+\frac { 1 }{ 10 } { \left( 1+\frac { z }{ 2 } \right) }^{ -1 }\\ f\left( z \right) =-\frac { 1 }{ 5z } \left( 1-\frac { 1 }{ { z }^{ 2 } } +{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 2 }-{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 3 }+.......... \right) +\\ \frac { 2 }{ 5{ z }^{ 2 } } \left( 1-\frac { 1 }{ { z }^{ 2 } } +{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 2 }-{ \left( \frac { 1 }{ { z }^{ 2 } } \right) }^{ 3 }+.......... \right) +\\ \frac { 1 }{ 10 } \left( 1-\frac { z }{ 2 } +{ \left( \frac { z }{ 2 } \right) }^{ 2 }-{ \left( \frac { z }{ 2 } \right) }^{ 3 }+....... \right) \\ f\left( z \right) =\frac { 1 }{ 10 } \sum _{ n=0 }^{ \infty }{ { \left( -1 \right) }^{ n }{ \left( \frac { z }{ 2 } \right) }^{ n } } +\frac { 2-z }{ { 5z }^{ 2 } } \sum _{ n=0 }^{ \infty }{ \frac { { \left( -1 \right) }^{ n } }{ { z }^{ 2n } } }
उपर्युक्त सवाल के हल को सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions) को समझा जा सकता है।
Question-2.फलन f\left( z \right) =\frac { { z }^{ 2 }+1 }{ z\left( { z }^{ 2 }-3z+2 \right) } का क्षेत्र \left| z+1 \right| >3 में z+1 की घातों में लौरां श्रेणी प्रसार प्राप्त करो।
(Obtain the Laurent series expansion in power of (z+1) of the function f\left( z \right) =\frac { { z }^{ 2 }+1 }{ z\left( { z }^{ 2 }-3z+2 \right) } the region \left| z+1 \right| >3
Solution–f\left( z \right) =\frac { { z }^{ 2 }+1 }{ z\left( { z }^{ 2 }-3z+2 \right) } \\ \frac { { z }^{ 2 }+1 }{ z\left( { z }^{ 2 }-3z+2 \right) } =f\left( z \right) =\frac { { z }^{ 2 }+1 }{ z\left( { z }^{ 2 }-2z-z+2 \right) } \\ =\frac { { z }^{ 2 }+1 }{ z\left[ z\left( z-2 \right) -1\left( z-2 \right) \right] } \\ =\frac { { z }^{ 2 }+1 }{ z\left[ \left( z-2 \right) \left( z-1 \right) \right] } \\ =\frac { A }{ z } +\frac { B }{ z-1 } +\frac { C }{ z-2 } \\ { z }^{ 2 }+1=A\left( z-2 \right) \left( z-1 \right) +Bz\left( z-2 \right) +Cz\left( z-1 \right)
Put z=0 then 2A=1 \Rightarrow A=\frac { 1 }{ 2 }
Put z=1 then -B=2 \Rightarrow B=-2
Put z=2 then 2C=5 \Rightarrow C=\frac { 5 }{ 2 } \\ f\left( z \right) =\frac { 1 }{ 2z } +\frac { 2 }{ z-1 } +\frac { 5 }{ 2\left( z-2 \right) } \\ =\frac { 1 }{ -2\left[ 1-\left( z+1 \right) \right] } +\frac { 2 }{ \left[ 2-\left( z+1 \right) \right] } +\frac { 5 }{ 2\left( 3-\left( z+1 \right) \right) } \\ =\frac { 1 }{ 2\left( z+1 \right) \left[ 1-\frac { 1 }{ z+1 } \right] } -\frac { 2 }{ \left( z+1 \right) \left[ 1-\frac { 2 }{ z+1 } \right] } +\frac { 5 }{ 2\left( z+1 \right) \left( 1-\frac { 3 }{ z+1 } \right) } \\ =\frac { 1 }{ 2\left( z+1 \right) } { \left( 1-\frac { 1 }{ z+1 } \right) }^{ -1 }-\frac { 2 }{ \left( z+1 \right) } { \left( 1-\frac { 2 }{ z+1 } \right) }^{ -1 }+\frac { 5 }{ 2\left( z+1 \right) } { \left( 1-\frac { 3 }{ z+1 } \right) }^{ -1 }\\ f\left( z \right) =\frac { 1 }{ 2\left( z+1 \right) } \left( 1+\frac { 1 }{ z+1 } +{ \left( \frac { 1 }{ z+1 } \right) }^{ 2 }+{ \left( \frac { 1 }{ z+1 } \right) }^{ 3 }+.......... \right) -\\ \frac { 2 }{ z+1 } \left( 1+\frac { 2 }{ z+1 } +{ \left( \frac { 2 }{ z+1 } \right) }^{ 2 }+{ \left( \frac { 2 }{ z+1 } \right) }^{ 3 }+.......... \right) +\\ \frac { 5 }{ 2\left( z+1 \right) } \left( 1+\frac { 3 }{ z+1 } +{ \left( \frac { 3 }{ z+1 } \right) }^{ 2 }+{ \left( \frac { 3 }{ z+1 } \right) }^{ 3 }+....... \right) \\ f\left( z \right) =\frac { 1 }{ 2\left( z+1 \right) } \sum _{ n=0 }^{ \infty }{ { \left( \frac { 1 }{ z+1 } \right) }^{ n } } -\frac { 2 }{ z+1 } \sum _{ n=0 }^{ \infty }{ { \left( \frac { 2 }{ z+1 } \right) }^{ n } } +\frac { 5 }{ 2\left( z+1 \right) } \sum _{ n=0 }^{ \infty }{ { \left( \frac { 3 }{ z+1 } \right) }^{ n } } \\ =\frac { 1 }{ 2 } \left[ \sum _{ n=0 }^{ \infty }{ { \left( 1-{ 2 }^{ n+2 }+5.{ 3 }^{ n } \right) } } { \left( z+1 \right) }^{ -\left( n+1 \right) } \right]
उपर्युक्त सवालों के हल द्वारा सम्मिश्र फलनों के लिए लौरां प्रमेय (Laurent theorem for complex functions) को समझा जा सकता है।
Also Read This Article:-power series expansion by Taylor theorem
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |