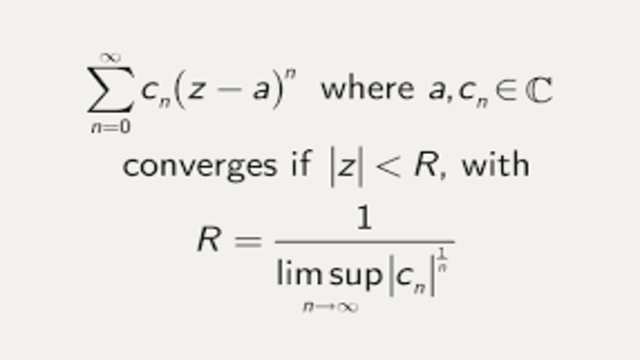Cauchy-Hadamard Theorem
1.कोशी-हाडामार्ड प्रमेय (Cauchy-Hadamard Theorem),सम्मिश्र विश्लेषण में हाडामार्ड प्रमेय (Hadamard theorem in complex analysis)-
कोशी-हाडामार्ड प्रमेय (Cauchy-Hadamard Theorem) को सिद्ध करके उसके आधार पर अर्थात् कोशी-हाडामार्ड सूत्र से घात श्रेणी की अभिसरण त्रिज्या ज्ञात करेंगे।
वृत्त \left| Z \right| =R,घात श्रेणी\sum { { a }_{ n } } { Z }^{ n } का अभिसरण वृत्त कहलाता है।यदि इसके भीतरी भाग \left| Z \right| <Rमें वे समस्त z के मान विद्यमान हैं जिनके लिए घात श्रेणी अभिसारी है। त्रिज्या R को इस वृत्त की अभिसारी त्रिज्या कहते हैं।
उपर्युक्त से स्पष्ट है कि अभिसरण वृत्त \left| Z \right| =Rके अंदर घात श्रेणी निरपेक्ष एवं एक समान अभिसारी होती है।इसके बाहर श्रेणी अपसारी होगी तथा वृत्त की परिसीमा पर श्रेणी अभिसारी या अपसारी हो सकती है।यदि घात श्रेणी \sum { { a }_{ n } } { Z }^{ n }की अभिसारी त्रिज्या R हो तो
\frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ sup{ \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } } }
इसे हम अभिसारी त्रिज्या के लिए हाडामार्ड सूत्र कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Cauchy-Riemann Equations
2.हाडामार्ड फार्मूला प्रमाण (Hadamard formula proof)-
हाडामार्ड प्रमेय कथन (Hadamard theorem statement),हाडामार्ड प्रमेय का कथन करें (State the Hadamard theorem),हाडामार्ड प्रमेय का कथन करें और प्रमाणित करें (State and prove Hadamard theorem)-
प्रत्येक घात श्रेणी \sum { { a }_{ n } } { Z }^{ n } के लिए एक वास्तविक संख्या R (0\le R<\infty )विद्यमान होती है जिसके निम्न गुणधर्म होते हैं:
(1.)प्रत्येक\left| Z \right| <R के लिए श्रेणी निरपेक्ष अभिसारी है।
(2.)\left| Z \right| \le \rho (0\le \rho <R) के लिए श्रेणी एकसमान अभिसारी है।
(3.)यदि \left| Z \right| >R हो तो श्रेणी का प्रत्येक पद अपरिबद्ध होता है एवं श्रेणी अपसारी होती है।
(For every power series \sum { { a }_{ n } } { Z }^{ n } there exists a real number R(0\le R<\infty ) with following properties:
(1.)The series converges absolutely for every \left| Z \right| <R.
(2.)If\left| Z \right| \le \rho (0\le \rho <R),the series converges uniformly for.
(3.)If \left| Z \right| >R,the terms of the series are unbounded and series is consequently divergent.)
उपपत्ति (Proof):माना कि\frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ sup{ \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } } }…(1)
(1.)माना कि\left| Z \right| <R तो एक \rho इस प्रकार विद्यमान होगा कि \left| Z \right| <\rho <R\Rightarrow (\frac { 1 }{ \rho } )>(\frac { 1 }{ R } )
अब (1) से स्पष्ट है कि एक धनात्मक पूर्णांक { n }_{ 0 } इस प्रकार विद्यमान है कि { \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } }<(\frac { 1 }{ \rho } )
अर्थात् \left| { a }_{ n } \right| <(\frac { 1 }{ { \rho }^{ n } } ),\nvdash n\ge { n }_{ 0 }\\ \left| { a }_{ n }{ Z }^{ n } \right| <{ (\frac { \left| Z \right| }{ \rho } ) }^{ n },\nvdash n\ge { n }_{ 0 }
परंतु \overset { \infty }{ \underset { n=0 }{ \sum { \quad } } } { (\frac { \left| Z \right| }{ \rho } ) }^{ n } एक गुणोत्तर श्रेणी है जिसका सार्व अनुपात 1 से कम है क्योंकि \left| Z \right| <\rho फलस्वरूप यह अभिसारी श्रेणी है।तुलना परीक्षण से, श्रेणी \sum { \left| { a }_{ n }{ Z }^{ n } \right| } भी अभिसारी श्रेणी है। अतः घात श्रेणी \sum { { a }_{ n }{ Z }^{ n } } उन सभी z के लिए निरपेक्ष अभिसारी है जिनके लिए \left| Z \right| <R
(2.)माना कि0\le \rho <R तथा { \rho }^{ \prime } का चयन इस प्रकार किया कि { \rho }^{ \prime }<\rho <\infty
अब (1) से अनुगत है कि
\left| { a }_{ n } \right| \le (\frac { 1 }{ { \rho }^{ n } } ),\nvdash n\ge { n }_{ 0 }
अतः \left| { a }_{ n }{ Z }^{ n } \right| \le { (\frac { \left| Z \right| }{ \rho } ) }^{ n }<{ (\frac { { \rho }^{ \prime } }{ \rho } ) }^{ n }[\because \left| z \right| \le { \rho }^{ \prime }<\rho ]
अब धनात्मक अचर संख्याओं की श्रेणी \sum { \quad } { (\frac { { \rho }^{ \prime } }{ \rho } ) }^{ n } अभिसारी है क्योंकि यह यह गुणोत्तर श्रेणी है तथा इसका सार्व अनुपात\frac { { \rho }^{ \prime } }{ \rho } <1 है।अतः वायर्स्ट्रास M-परीक्षण से घात श्रेणी\sum { \quad } { a }_{ n }{ Z }^{ n },\left| Z \right| \le \rho <R के लिए एकसमान अभिसारी है।
(3.)यदि \left| Z \right| >Rहो, तो \rho का चयन इस प्रकार से किया ताकिR<\rho <\left| Z \right|\\ \frac { 1 }{ R } >\frac { 1 }{ \rho }
चूंकि \frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ sup{ \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } } }
अतः स्वेच्छाग्रहीत बड़ा n इस प्रकार विद्यमान होगा कि { \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } }>\frac { 1 }{ \rho }
अर्थात् \left| { a }_{ n } \right| >(\frac { 1 }{ { \rho }^{ n } } )
फलत:\left| { a }_{ n }{ Z }^{ n } \right| >{ (\frac { \left| Z \right| }{ \rho } ) }^{ n },अनंत मानों के लिए चूंकि श्रेणी के पद अपरिबद्ध है अतः श्रेणी अपसारी है।
द्वितीय कोशी प्रमेय के अनुसार यदि \{ { a }_{ n }\} एक अनुक्रम धनात्मक चरों का है,तब
lim{ \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } }=_{ n\rightarrow \infty }^{ lim }\left| \frac { { a }_{ n }+1 }{ { a }_{ n } } \right|
बशर्ते दक्षिण पक्ष की सीमा परिमित या अपरिमित रूप से अस्तित्व हो।
R=_{ n\rightarrow \infty }^{ lim }\left| \frac { { a }_{ n } }{ { a }_{ n }+1 } \right|
3.कोशी-हाडामार्ड प्रमेय उदाहरण (Cauchy-Hadamard Theorem examples)-
निम्न घात श्रेणियों के अभिसरण त्रिज्या ज्ञात कीजिए:
(Find radius of convergence of the following series:)
Example-1.\overset { \infty }{ \underset { n=1 }{ \sum { \quad } } } \frac { 1 }{ { n }^{ n } } { z }^{ n }
Solution-\frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } }\\ \frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ \left| \frac { 1 }{ { n }^{ n } } \right| }^{ \frac { 1 }{ n } }\\ =_{ n\rightarrow \infty }^{ lim }{ \left| \frac { 1 }{ { n }^{ n } } \right| }\\ =_{ n\rightarrow \infty }^{ lim }\frac { 1 }{ n } \\ \frac { 1 }{ R } =0
अभिसरण त्रिज्या R=\infty
Example-2.\sum { \frac { n! }{ { n }^{ n } } } { z }^{ n }
Solution-{ a }_{ n }=\frac { n! }{ { n }^{ n } } \\ \left| { a }_{ n } \right| =\left| \frac { n! }{ { n }^{ n } } \right| \\ \left| { a }_{ n+1 } \right| =\left| \frac { (n+1)! }{ { (n+1) }^{ n+1 } } \right| \\ R=_{ n\rightarrow \infty }^{ lim }\left| \frac { { a }_{ n } }{ { a }_{ n }+1 } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { n! }{ { n }^{ n } } \frac { { (n+1) }^{ n+1 } }{ (n+1)! } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { n! }{ { n }^{ n } } \frac { { (n+1) }^{ n }.(n+1) }{ (n+1).n! } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { { (n+1) }^{ n } }{ { n }^{ n } } \right| \\ =_{ n\rightarrow \infty }^{ lim }\frac { { { n }^{ n }(1+\frac { 1 }{ n } ) }^{ n } }{ { n }^{ n } } \\ =_{ n\rightarrow \infty }^{ lim }{ (1+\frac { 1 }{ n } ) }^{ n }\\ R=e
Example-3.\overset { \infty }{ \underset { n=1 }{ \sum { \quad } } } { (3+4i) }^{ n }{ z }^{ n }
Solution-\frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ \left| { a }_{ n } \right| }^{ \frac { 1 }{ n } }\\ \frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ \left| { (3+4i) }^{ n } \right| }^{ \frac { 1 }{ n } }\\ \frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }{ \sqrt { { 3 }^{ 2 }+{ 4 }^{ 2 } } }\\ \frac { 1 }{ R } =_{ n\rightarrow \infty }^{ lim }\sqrt { 9+16 } \\ \frac { 1 }{ R } =\sqrt { 25 } \\ \frac { 1 }{ R } =5\\ R=\frac { 1 }{ 5 }
Example-4.1+\frac { a.b }{ 1.c } z+\frac { a(a+1).b(b+1) }{ 1.2....c(c+1) } .{ z }^{ 2 }+....
Solution-1+\frac { a.b }{ 1.c } z+\frac { a(a+1).b(b+1) }{ 1.2....c(c+1) } .{ z }^{ 2 }+....\\ { a }_{ n }=\frac { a(a+1)......a+(n-1)b(b+1)....b+(n-1) }{ 1.2.......nc(c+1).....c+(n-1) } \\ \left| { a }_{ n } \right| =\left| \frac { a(a+1)......a+(n-1)b(b+1)....b+(n-1) }{ 1.2.......nc(c+1).....c+(n-1) } \right| \\ \left| { a }_{ n+1 } \right| =\left| \frac { a(a+1)......a+(n-1)(a+n)b(b+1)....b+(n-1)(b+n) }{ 1.2.......n(n+1)c(c+1).....c+(n-1)(c+n) } \right| \\ R=_{ n\rightarrow \infty }^{ lim }\left| \frac { { a }_{ n } }{ { a }_{ n }+1 } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { { (n+1) }(c+n) }{ (a+n)(b+n) } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { (1+\frac { 1 }{ n } )(1+\frac { c }{ n } ) }{ (1+\frac { a }{ n } )(1+\frac { b }{ n } ) } \right| \\ R=1
Example-5.\overset { \infty }{ \underset { n=1 }{ \sum { \quad } } } \frac { { z }^{ n } }{ { n }^{ p } }
Solution-{ a }_{ n }=\frac { 1 }{ { n }^{ p } } \\ \left| { a }_{ n } \right| =\left| \frac { 1 }{ { n }^{ p } } \right| \\ \left| { a }_{ n+1 } \right| =\left| \frac { 1 }{ { (n+1) }^{ p } } \right| \\ R=_{ n\rightarrow \infty }^{ lim }\left| \frac { { a }_{ n } }{ { a }_{ n }+1 } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { { (n+1) }^{ p } }{ { n }^{ p } } \right| \\ =_{ n\rightarrow \infty }^{ lim }\left| \frac { { { n }^{ p }(1+\frac { 1 }{ n } ) }^{ p } }{ { n }^{ p } } \right| \\ R=1
इन उदाहरणों के द्वारा कोशी-हाडामार्ड प्रमेय (Cauchy-Hadamard Theorem) को समझ सकते हैं।
4.कोशी-हाडामार्ड प्रमेय समस्याएं (Cauchy-Hadamard Theorem problems)-
निम्न घात श्रेणियों के अभिसरण त्रिज्या ज्ञात कीजिए:
(Find radius of convergence of the following series:)
(1)\sum { { (1+\frac { 1 }{ n } ) }^{ { n }^{ 2 } }{ z }^{ n } } \\ (2)\sum { \frac { { (n!) }^{ 2 } }{ (2n)! } { z }^{ n } } \\ (3)\sum { \frac { n+1 }{ (n+2)(n+3) } { z }^{ n } } \\ (4)\sum { \frac { { z }^{ n } }{ { z }^{ n }+1 } } \\ (5)\sum { { 2 }^{ \sqrt { n } }.{ z }^{ n } } \\ (6)\sum { \frac { { 2 }^{ -n } }{ 1+i{ n }^{ 2 } } { z }^{ n } } \\ (7)\sum { (\frac { n\sqrt { 2 } +i }{ 1+2in } ) } { z }^{ n }\\ (8)\sum { \frac { 2+in }{ { 2 }^{ n } } } \\ (9)\sum { \frac { { (-1) }^{ n } }{ n } } { (z-2i) }^{ n }\\ (10)\sum { { (\frac { { z }^{ 2 }+1 }{ i+1 } ) }^{ n }{ n }^{ 2 } }
उत्तर-
(1) \frac { 1 }{ e } (2.) 4 (3.) 1 (4.) 2 (5.) 0 (6.) 2 (7.) 1 (8.) 1 (9.) 1(10.) \sqrt { 2 }
उपर्युक्त समस्याओं को हल करने पर कोशी-हाडामार्ड प्रमेय (Cauchy-Hadamard Theorem) को ओर ठीक से समझ सकते हैं।
5.कोशी-हामामार्ड मापदण्ड (Cauchy Hadamard criterion)-
गणित में, कोशी-हाडार्ड प्रमेय एक सम्मिश्र विश्लेषण का परिणाम है जिसका नाम फ्रांसीसी गणितज्ञों ऑगस्टिन लुइस कोशी और जैक्स हाडामार्ड के नाम पर रखा गया है, जो एक घात श्रृंखला के अभिसरण का वर्णन करता है।यह 1821 में कोशी द्वारा प्रकाशित किया गया था, लेकिन हाडामार्ड ने इसे फिर से खोजे जाने तक अपेक्षाकृत अज्ञात बना रहा।
6.रूट टेस्ट (Root test)-
गणित में, रूट परीक्षण एक अनंत श्रृंखला के अभिसरण (अभिसरण परीक्षण) के लिए एक मानदंड है। यह उस मात्रा पर निर्भर करता है जहां श्रृंखला की शर्तें होती हैं और बताती हैं कि श्रृंखला निरपेक्ष अभिसारी होती है यदि यह मात्रा एक से कम है, लेकिन यदि यह एक से अधिक है, तो इसे अपसारी होती है।
7.आबेल प्रमेय (abel theorem)-
आबेल का प्रमेय कहता है कि यदि कोई घात श्रृंखला (-1,1) और x = 1 पर भी अभिसारी हो जाती है, तो x = 1 पर इसका मान 1 की बाईं ओर से सांतत्य से निर्धारित होता है।आपको पता होना चाहिए कि श्रृंखला x = 1 से पहले अभिसारी होती है आप आबेल की प्रमेय लागू कर सकते हैं।
8.हाडामार्ड गुणा (Hadamard product)-
गणित में, Hadamard गुणा (जिसे तत्व-वार, एंट्रीवाइज़ या Schur गुणा के रूप में भी जाना जाता है) एक द्विआधारी ऑपरेशन है जो समान आयामों के दो मैट्रिक्स लेता है और ऑपरेंड्स के समान आयाम का एक और मैट्रिक्स उत्पन्न करता है, जहां प्रत्येक तत्व i, j दो मूल मेट्रिसेस के तत्वों i ,jका तत्व है।
Also Read This Article:-Harmonic function in complex analysis
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |