Area of Triangles Class 9
1.त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9),एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों का क्षेत्रफल कक्षा 9 (Area of Triangles Between Same Base and Same Parallel Lines Class 9):
त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9) के इस आर्टिकल में एक ही आधार (या बराबर आधारों) और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल को उदाहरणों के द्वारा समझेंगे।
प्रमेय (Theorem):9.2.एक ही आधार (या बराबर आधारों) और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
दिया है (Given): \triangle ABC और \triangle DBC एक ही आधार BC पर तथा समान्तर रेखाओं BC एवं AF के मध्य में स्थित हैं।
सिद्ध करना है (To Prove):क्षेत्रफल (\triangle ABC)=क्षेत्रफल ( \triangle DBC)
रचना (Construction):C से क्रमशः AB एवं BD के समान्तर रेखाएँ CE तथा CF खींची।
उपपत्ति (Proof):ABCE और DBCF समान्तर रेखाओं BC और AF के मध्य स्थित हैं अतः
क्षेत्रफल (स.च. ABCE)=क्षेत्रफल (समान्तर चतुर्भुज DBCF) …. (1)
AC समान्तर चतुर्भुज ABCE का विकर्ण है अतः
क्षेत्रफल \triangle ABC=\frac{1}{2} क्षेत्रफल (समान्तर चतुर्भुज ABCE) …. (2)
इसी प्रकार DC समान्तर चतुर्भुज DBCF का विकर्ण है अतः
क्षेत्रफल \triangle DBC=\frac{1}{2} क्षेत्रफल (समान्तर चतुर्भुज DBCE)… (3)
समीकरण (1),(2) और (3) सेः
क्षेत्रफल (\triangle ABC)=क्षेत्रफल ( \triangle DBC)
प्रमेय (Theorem):9.3.एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समान्तर रेखाओं के बीच स्थित होते हैं।
दिया है (Given): \triangle ABC एवं \triangle ABD जो एक ही आधार AB पर स्थित हैं तथा ar(\triangle ABC)=ar(\triangle ABD)
सिद्ध करना है (To Prove): AB \| CD
रचना (Construction):बिन्दु C व D से AB पर लम्ब क्रमशः CF व DE खींचा।
उपपत्ति (Proof):ar(\triangle ABC)=ar(\triangle ABD) (दिया है)
\therefore \frac{1}{2} \times A B \times C F=\frac{1}{2} \times A B \times D E \\ \Rightarrow C F=D E
अतः AB \| CD
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Area of Parallelograms Class 9
2.त्रिभुजों के क्षेत्रफल कक्षा 9 पर आधारित उदाहरण (Examples Based on Area of Triangles Class 9):
Example:1.आकृति में, \triangle ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है।दर्शाइए कि ar(ABE)=ar(ACE)
Solution:दिया है (Given):E, \triangle ABC की माध्यिका AD पर कोई बिन्दु है।
सिद्ध करना है (To Prove): ar(\triangle ABE)=ar(\triangle ACE)
उपपत्ति (Proof): \triangle ABC में AD माध्यिका है।
ar(\triangle ABD)=ar(\triangle ACD) \cdots(1)
(त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करती है)
\triangle EBC में ED माध्यिका है।
\therefore ar(\triangle EBD)=ar(\triangle ECD) \cdots(2)
(त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है)
समीकरण (1) में से (2) घटाने परः
ar(\triangle ABC)-ar(\triangle EBD)=ar(\triangle ACD)-ar(\triangle ECD) \\ \Rightarrow ar(\triangle ABE)=ar(\triangle ACE)
Example:2. \triangle ABC में,E माध्यिका AD का मध्य-बिन्दु है।दर्शाइए कि \operatorname{ar}(\triangle BED)=\frac{1}{4} \operatorname{ar}(\triangle ABC) है।
दिया है (Given): \triangle ABC में,E माध्यिका AD का मध्य-बिन्दु है।
सिद्ध करना है (To Prove): \operatorname{ar}(\triangle BED)=\frac{1}{4} \operatorname{ar}(\triangle ABC)
उपपत्ति (Proof): \triangle ABC में AD माध्यिका है।
\therefore \operatorname{ar}(\triangle ABD)=\operatorname{ar}(\triangle ACD)=\frac{1}{2} \operatorname{ar}(\triangle ABC) \cdots(1)
(त्रिभुज की माध्यिका उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है)
\triangle ABD में BE एक माध्यिका है।
\therefore \operatorname{ar}(\triangle BED)=\operatorname{ar}(\triangle BEA)=\frac{1}{2} \operatorname{ar}(\triangle ABD) \cdots(2)
( \because त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है)
समीकरण (1) व (2) सेः
\operatorname{ar}(\triangle BED)=\frac{1}{2} \operatorname{ar}(\triangle ABD)=\frac{1}{2} \times \frac{1}{2} \times \operatorname{ar}(\triangle ABC) \\ \Rightarrow \operatorname{ar}(\triangle BED)=\frac{1}{4} \operatorname{ar}(\triangle ABC)
Example:3.दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
दिया है (Given):ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण AC और BD हैं जो O पर प्रतिच्छेदन करते हैं,इसे चार त्रिभुजों \triangle OAB, \triangle OBC,\triangle OCD और \triangle OAD में विभाजित करते हैं।
सिद्ध करना है (To Prove): \operatorname{ar}(\triangle OAB)=\operatorname{ar}(\triangle OBC)=\operatorname{ar}(\triangle OCD) \\ =\operatorname{ar}(\triangle ODA)
रचना (Construction): BE \perp AC खींचा।
उपपत्ति (Proof):चूँकि ABCD एक समान्तर चतुर्भुज है।
\therefore OA=OC और OB=OD
(समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।)
अतः \operatorname{ar}(\triangle OAB) =\frac{1}{2} \times \text {आधार} \times \text{ऊँचाई} \\ =\frac{1}{2} \times OA \times BE
और \operatorname{ar}(\triangle OBC)=\frac{1}{2} \times OC \times BE
परन्तु OA=OC
\therefore \operatorname{ar}(\triangle OAB)=\operatorname{ar}(\triangle OBC) \cdots(1)
इसी प्रकार \operatorname{ar}(\triangle OBC)=\operatorname{ar}(\triangle OCD) \cdots(2)
और ar(\triangle OCD)=\operatorname{ar}(\triangle ODA) \cdots(3)
समीकरण (1),(2) और (3) सेः
\operatorname{ar}(\triangle OAB)=\operatorname{ar}(\triangle OBC)=\operatorname{ar}(\triangle OCD) \\ =\operatorname{ar}(\triangle ODA)
Example:4.आकृति में,ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं।यदि रेखाखण्ड CD रेखाखण्ड AB से बिन्दु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC)=ar(ABD) है।
Solution:दिया है (Given):ABC और ABD एक ही आधार AB पर दो त्रिभुज हैं।रेखाखण्ड CD रेखाखण्ड AB से बिन्दु O पर समद्विभाजित होता है।
सिद्ध करना है (To Prove):ar(ABC)=ar(ABD)
उपपत्ति (Proof): \because रेखाखण्ड CD,AB के द्वारा O पर समद्विभाजित होता है।
\therefore OC=OD
\triangle ACD में AO माध्यिका है।
\therefore ar(AOC)=ar(AOD) … (1)
( \because माध्यिका किसी त्रिभुज को दो समान क्षेत्रफलों वाले त्रिभुजों में बाँटता है)
इसी प्रकार, \triangle BCD में BO माध्यिका है।
\therefore ar(BOC)=ar(BOD) … (2)
(\because माध्यिका किसी त्रिभुज को दो समान क्षेत्रफलों वाले त्रिभुजों में बाँटता है)
समीकरण (1) व (2) को जोड़ने परः
ar(AOC)+ar(BOC)=ar(AOD)+ar(BOD)
\Rightarrow ar(ABC)=ar(ABD)
Example:5.D,E और F क्रमशः ABC की भुजाओं BC,CA और AB के मध्य-बिन्दु हैं।दर्शाइए कि
(i)BDEF एक समान्तर चतुर्भुज है
(ii) \operatorname{ar}(DEF)=\frac{1}{4} \operatorname{ar}(ABC)
(iii) \operatorname{ar}(BDEF)=\frac{1}{2} \operatorname{ar}(ABC)
दिया है (Given): \triangle ABC में D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य-बिन्दु है।
सिद्ध करना है (To Prove):(i)BDEF एक समान्तर चतुर्भुज है
(ii) \operatorname{ar}(DEF)=\frac{1}{4} \operatorname{ar}(ABC)
(iii) \operatorname{ar}(BDEF)=\frac{1}{2} \operatorname{ar}(ABC)
उपपत्ति (Proof): \triangle ABC में
EF\|BC [मध्य-बिन्दु प्रमेय द्वारा,चूँकि E व F क्रमशः AC और AB के मध्य-बिन्दु है]
\therefore E F \| B D \cdots(1)
साथ ही ED \| AB [मध्य-बिन्दु प्रमेय द्वारा,चूँकि E व D क्रमशः AC और BC के मध्य-बिन्दु है]
\therefore ED \| AF \cdots(2)
समीकरण (1) व (2) सेः
BDEF एक समान्तर चतुर्भुज है।
(ii)इसी प्रकार,FDCE और AFDE समान्तर चतुर्भुज हैं।
ar(FBD)=ar(DEF) [\because FD समान्तर चतुर्भुज BDEF का एक विकर्ण है]
ar(DEC)=ar(DEF) [\because ED समान्तर चतुर्भुज FDCE का एक विकर्ण है]
और ar(AFE)=ar(DEF) [ \because FE समान्तर चतुर्भुज AFDE का एक विकर्ण है]
\therefore ar(FBD)=ar(DEC)=ar(AFE)=ar(DEF) \\ \Rightarrow ar(DEF)=\frac{1}{4} ar(ABC)
(iii)साथ ही, \operatorname{ar}(BDEF)=2ar(DEF) \\ \operatorname{ar}(BDEF)=2 \times \frac{1}{4} \operatorname{ar}(ABC) \\ \Rightarrow \operatorname{ar}(BDEF)=\frac{1}{2} \operatorname{ar}(ABC)
Example:6.आकृति में,चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB=OD है।यदि AB=CD है, तो दर्शाइए कि
(i)ar(DOC)=ar(AOB)
(ii)ar(DCB)=ar(ACB)
(iii) DA || CB या ABCD एक समान्तर चतुर्भुज है।
दिया है (Given):चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB=OD
सिद्ध करना है (To Prove):(i)ar(DOC)=ar(AOB)
(ii)ar(DCB)=ar(ACB)
(iii)या ABCD एक समान्तर चतुर्भुज है।
रचना (To Construction):DN \perp AC और B M \perp AC खींचा
उपपत्ति (Proof):(i)\triangle DON और \triangle BOM में
\angle DNO=\angle BMO=90^{\circ} \\ \angle DON=\angle BOM (सम्मुख कोण)
OD=OB (दिया है)
AAS सर्वांगसमता गुणधर्म से
\triangle DON \cong \triangle BOM \cdots(1)
DN=BM (CPCT)
\triangle DCN और \triangle BAM में
\angle DNC=\angle BMA=90^{\circ}
DC=AB (दिया है)
DN=BM (CPCT से)
RHS सर्वांगसमता गुणधर्म से
\triangle DCN \cong \triangle BAM \cdots(2)
समीकरण (1) व (2) सेः
ar(DON)+ar(DCN)=ar(BOM)+ar(BAM)
\Rightarrow ar(DOC)=ar(AOB)
(ii) \therefore ar(DOC)=ar(AOB)
दोनों पक्षों में ar(BOC) जोड़ने परः
ar(DOC)+ar(BOC)=ar(AOB)+ar(BOC)
\Rightarrow ar(DCB)=ar(ACB)
(iii) \triangle DCB और \triangle ACB के क्षेत्रफल और आधार समान हैं।अतः उनके त्रिभुज एक ही समान्तर रेखाओं के मध्य स्थित होंगे।
\Rightarrow D A \| CB अर्थात् ABCD समान्तर चतुर्भुज है।
Example:7.बिन्दु D और E क्रमशः की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC)=ar(EBC) है।दर्शाइए कि DE \| BC है।
Solution:दिया है (Given):की भुजाओं AB और AC पर D व E इस प्रकार स्थित हैं कि ar(DBC)=ar(EBC)
सिद्ध करना है (To Prove): DE \| BC
उपपत्ति (Proof):चूँकि \triangle DBC और \triangle EBC के क्षेत्रफल बराबर हैं और दोनों के आधार बराबर हैं।अतः वे एक ही समान्तर रेखाओं के मध्य स्थित होंगे फलतः DE \| BC
Example:8.XY त्रिभुज ABC की भुजा BC के समान्तर एक रेखा है।यदि BE \| AC और CF \| AB रेखा XY से क्रमशः E और F पर मिलती है, तो दर्शाइए किः
ar(ABE)=ar(ACF)
Solution:दिया है (Given):की भुजा BC के समान्तर एक रेखा XY इस प्रकार है कि BE \| AC और CF \| AB रेखा XY से क्रमशः E व F पर मिलती है।
सिद्ध करना है (To Prove):ar(ABE)=ar(ACF)
उपपत्ति (Proof):चूँकि XY \| BC और BE \| CY
\therefore BCYE एक समान्तर चतुर्भुज है।
चूँकि और समान्तर चतुर्भुज BCYE एक ही आधार BE और एक ही समान्तर रेखाओं BE और AC के मध्य स्थित हैं।
\therefore \operatorname{ar}(ABE)=\frac{1}{2} ar(BCYE) \cdots(1)
अब CF \| AB तथा XY \| BC \\ \Rightarrow CF \| AB तथा XF \| BC \\ \Rightarrow BCFX एक समान्तर चतुर्भुज है।
चूँकि और समान्तर चतुर्भुज BCFX एक ही आधार CF और एक ही समान्तर रेखाओं AB और FC के मध्य स्थित हैं।
\therefore ar(ACF)=\frac{1}{2} ar(BCFX) \cdots(2)
लेकिन समान्तर चतुर्भुज BCFX और समान्तर चतुर्भुज BCYE एक ही आधार BC पर और एक ही समान्तर रेखाओं BC और EF के मध्य स्थित हैं।
\therefore ar(BCFX)=ar(BCYE)…..(3)
समीकरण (1),(2) और (3) सेः
\operatorname{ar}(\triangle ABE)=\operatorname{ar}(\triangle ACF)
Example:9.समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है।A से होकर CP के समान्तर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समान्तर चतुर्भुज PBQR को पूरा किया गया है (देखिए आकृति)।दर्शाइए कि ar(ABCD)=ar(PBQR) है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD की भुजा AB को एक बिन्दु P तक बढ़ाया गया है तथा A से होकर CP के समान्तर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है।PBQR समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):ar(ABCD)=ar(PBQR)
रचना (Construction):AC और PQ को मिलाया।
उपपत्ति (Proof):चूँकि AC और PQ क्रमशः समान्तर चतुर्भुज ABCD और समान्तर चतुर्भुज PBQR के विकर्ण हैं।
\therefore \operatorname{ar}(ABC)=\frac{1}{2} \operatorname{ar}(ABCD) \cdots(1)
और \operatorname{ar}(PBQ)=\frac{1}{2} \operatorname{ar}(PBRQ) \cdots(2)
अब \triangle ACQ और \triangle AQP एक ही आधार AQ पर और एक ही समान्तर रेखाओं AQ और CP के मध्य स्थित हैं।
\therefore ar(ACQ)=ar(AQP)
\Rightarrow ar(ACQ)-ar(ABQ)=ar(AQP)-ar(ABQ)
[ar(ABQ) को दोनों पक्षों में घटाने पर]
\Rightarrow ar(ABC)=ar(BPQ)
\Rightarrow \frac{1}{2} \operatorname{ar}(ABCD)=\frac{1}{2} \operatorname{ar}(PBRQ)[(1) व (2) से ]
\Rightarrow \operatorname{ar}(ABCD)=\operatorname{ar}(PBRQ)
Example:10.एक समलम्ब ABCD, जिसमें है,के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।दर्शाइए कि ar(AOD)=ar(BOC) है।
Solution:दिया है (Given):समलम्ब चतुर्भुज ABCD में AB || DC तथा विकर्ण AC और BD, O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove):ar(AOD)=ar(BOC)
उपपत्ति (Proof):समलम्ब ABCD में AB || DC है,के विकर्ण AC और BC, O पर प्रतिच्छेद करते हैं।
\therefore \triangle ABC और \triangle ABD एक ही आधार और एक ही समान्तर रेखाओं के मध्य स्थित हैं।
\therefore ar(ABD)=ar(ABC)
दोनों पक्षों में ar(AOB) घटाने परः
\Rightarrow ar(ABD)-ar(AOB)=ar(ABC)-ar(AOB)
\Rightarrow ar(AOD)=ar(BOC)
Example:11.आकृति में ABCDE एक पंचभुज है।B से होकर AC के समान्तर खींची गई DC को F पर मिलती है।दर्शाइए कि
(i)ar(ACB)=ar(ACF)
(ii)ar(AEDF)=ar(ABCDE)
Solution:दिया है (Given):ABCDE एक पंचभुज है। B से होकर AC, BF || AC
सिद्ध करना है (To Prove):(i)ar(ACB)=ar(ACF)
(ii)ar(AEDF)=ar(ABCDE)
उपपत्ति (Proof):(i)चूँकि \triangle ACB और \triangle ACF एक ही आधार AC और एक ही समान्तर रेखाओं AC और BF के मध्य स्थित हैं।
\therefore ar(ACB)=ar(ACF)
(ii)दोनों पक्षों में ar(ACDE) जोड़ने परः
ar(ACB)+ar(ACDE)=ar(ACF)+ar(ACDE)
\Rightarrow ar(AEDF)=ar(ABCDE)
Example:12.गाँव के निवासी इतवारी के पास एक चतुभुर्जाकार भूखण्ड था।उस गाँव की ग्राम पंचायत ने उसके भूखण्ड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके।इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखण्ड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखण्ड त्रिभुजाकार हो जाए।स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
Solution:माना ABCD एक चतुर्भुजाकार भूखण्ड है।DE को E पर CA के समान्तर मिलाने के लिए BA को आगे बढ़ाया।
इस प्रकार \triangle EAC और \triangle ADC एक ही समान्तर रेखाओं DE और CA के बीच स्थिति में आ जाते हैं।
\therefore ar(EAC)=ar(ADC)
अब ar(ABCD)=ar(ABC)+ar(ACD)
=ar(ABC)+ar(ADC)
=ar(ABC)+ar(EAC)
=ar(EBC)
अर्थात् चतुर्भुज ABCD=\triangle EBC
Example:13.ABCD एक समलम्ब है,जिसमें AB || DC है।AC के समान्तर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है।सिद्ध कीजिए कि ar(ADX)=ar(ACY) है।
Solution:दिया है (Given):समलम्ब ABCD में AB || DC है। और XY || AC है।
सिद्ध करना है (To Prove):ar(ADX)=ar(ACY)
रचना (Construction):XY को मिलाया।
उपपत्ति (Proof): \triangle ACX और \triangle ACY का आधार समान है और एक ही समान्तर रेखाओं AC और XY के मध्य स्थित हैं अतः
ar(ACX)=ar(ACY) …. (1)
\triangle ACX और \triangle ADX का आधार AX समान है और दोनों एक ही समान्तर रेखाओं AB और DC के मध्य स्थित हैं अतः
ar(ACX)=ar(ADX) … (2)
(1) व (2) सेः
ar(ADX)=ar(ACY)
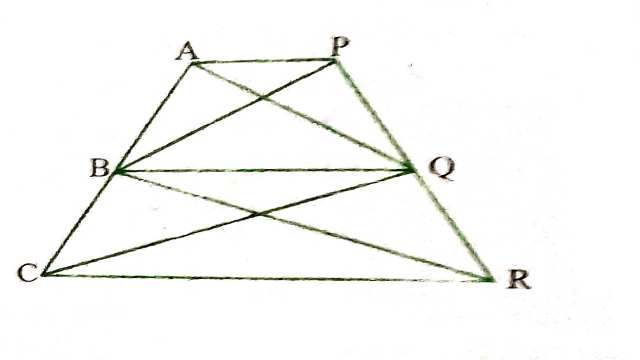
Example:14.आकृति में, AP\| BQ \| CR है।सिद्ध कीजिए कि ar(AQC)=ar(PBR) है।
Solution:दिया है (Given): AP\| BQ \| CR
सिद्ध करना है (To Prove):ar(AQC)=ar(PBR)
उपपत्ति (Proof):आकृति से
ar(AQC)=ar(AQB)+ar(BQC) … (1)
और ar(PBR)=ar(PBQ)+ar(QBR) …..(2)
और एक ही आधार BQ पर और एक ही समान्तर रेखाओं AP और BQ के बीच स्थित हैं अतः
ar(AQB)=ar(PBQ) …. (3)
\triangle AQB और \triangle PBQ एक ही आधार BQ और एक ही समान्तर रेखाओं BQ और CR के बीच स्थित हैं अतः
ar(BQC)=ar(QBR) …. (4)
समीकरण (3) और (4) को समीकरण (1) व (2) में प्रयोग करने परः
ar(AQC)=ar(PBR)
Example:15.चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(AOD)=ar(BOC) है।सिद्ध कीजिए कि ABCD एक समलम्ब है।
Solution:दिया है (Given):ABCD के विकर्ण AC और BD इस प्रकार प्रतिच्छेद करते हैं कि ar(AOD)=ar(BOC)
सिद्ध करना है (To Prove): AB || DC
उपपत्ति (Proof):ar(AOD)=ar(BOC) (दिया है)
दोनों पक्षों में ar(DOC) जोड़ने परः
ar(AOD)+ar(DOC)=ar(BOC)+ar(DOC)
\Rightarrow ar(ADC)=ar(BDC)
\Rightarrow \frac{1}{2} \times DC \times AL=\frac{1}{2} \times DC \times BM \\ \Rightarrow AL=BM \\ \Rightarrow AB || DC
अतः ABCD समलम्ब चतुर्भुज है।
Example:16.आकृति में ar(DRC)=ar(DPC) है और ar(BDP)=ar(ARC) है।दर्शाइए कि दोनो चतुर्भुज ABCD और DCPR समलम्ब हैं।
Solution:दिया है (Given):ar(DRC)=ar(DPC),ar(BDP)=ar(ARC)
सिद्ध करना है (To Prove):चतुर्भुज ABCD और DCPR समलम्ब हैं।
उपपत्ति (Proof):ar(DRC)=ar(DPC) (दिया है) … (2)
\triangle DRC तथा \triangle DPC एक ही आधार DC पर स्थित हैं तथा दोनों का क्षेत्रफल समान हैं अतः DC || RP
अतः DCPR समलम्ब चतुर्भुज है।
ar(BDP)=ar(ARC) (दिया है) … (2)
(2) में से (1) घटाने परः
ar(BDP)-ar(DPC)=ar(ARC)-ar(DRC)
ar(DBC)=ar(ACD)
\triangle DBC तथा \triangle ACD एक ही आधार DC पर स्थित हैं तथा दोनों का क्षेत्रफल समान हैं अतः AB || DC
अतः चतुर्भुज ABCD समलम्ब है।
उपर्युक्त उदाहरणों के द्वारा त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9),एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों का क्षेत्रफल कक्षा 9 (Area of Triangles Between Same Base and Same Parallel Lines Class 9) को समझ सकते हैं।
3.त्रिभुजों के क्षेत्रफल कक्षा 9 पर आधारित सवाल (Questions Based on Area of Triangles Class 9):
(1.)यदि एक त्रिभुज और समान्तर चतुर्भुज एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हों तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल समान्तर चतुर्भुज के क्षेत्रफल का आधा होता है।
(2.)समान्तर चतुर्भुज ABCD के अभ्यन्तर में P एक बिन्दु है।सिद्ध कीजिए किः
ar(\triangle ABP)+ar(\triangle DCP)=\frac{1}{2} ar(समान्तर चतुर्भुज ABCD)
उपर्युक्त सवालों को हल करने पर त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9),एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों का क्षेत्रफल कक्षा 9 (Area of Triangles Between Same Base and Same Parallel Lines Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Area of Parallelograms and Triangles
4.त्रिभुजों के क्षेत्रफल कक्षा 9 (Frequently Asked Questions Related to Area of Triangles Class 9),एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों का क्षेत्रफल कक्षा 9 (Area of Triangles Between Same Base and Same Parallel Lines Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सर्वांगसम क्षेत्रफल अभीगृहीत क्या है? (What is the Congruent Area Axiom?):
उत्तर:यदि \triangle ABC और \triangle PQR दो सर्वांगसम त्रिभुज हों तो
ar(प्रदेश \triangle ABC)=ar(प्रदेश \triangle PQR)
प्रश्न:2.क्षेत्रफल योग अभीगृहीत क्या है? (What is the Area Addition Axiom?):
उत्तर:यदि R_1 और R_2 दो बहुभुज प्रदेश हों जिसके सर्वनिष्ठ परिमित संख्या में बिन्दु और रेखाखण्ड हों और R=R_{1} \cup R_{2} तो \operatorname{ar}(R)= \operatorname{ar} \left(R_1\right)+ \operatorname{ar}\left(R_2\right)
प्रश्न:3.क्षेत्रफल एकदिष्ट अभीगृहीत क्या है? (What is the Area Monotone Axiom?):
उत्तर:यदि R_1,R_2 दो बहुभुज प्रदेश हों और R_1 \subset R_2 तो
\operatorname{ar}\left(R_1\right) \leq \operatorname{ar}\left(R_2\right)
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9),एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों का क्षेत्रफल कक्षा 9 (Area of Triangles Between Same Base and Same Parallel Lines Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Area of Triangles Class 9
त्रिभुजों के क्षेत्रफल कक्षा 9
(Area of Triangles Class 9)
Area of Triangles Class 9
त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9) के इस आर्टिकल में एक ही आधार (या बराबर
आधारों) और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल को उदाहरणों के द्वारा समझेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.