What is the Section Formula?
1.विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division),विभाजन सूत्र कक्षा 10 (Section formula class 10)-
विभाजन सूत्र क्या है? (What is the Section Formula?) समतल में स्थित दो बिन्दुओं को तीसरा बिन्दु जिस अनुपात में विभाजित करता है उसे विभाजन सूत्र कहते हैं।यह विभाजन दो प्रकार का होता है अन्त: विभाजन और बाह्य विभाजन।
इस आर्टिकल में अन्त:विभाजन और बाह्य विभाजन सूत्र विभाजन करने और उन पर आधारित उदाहरणों के द्वारा विभाजन सूत्र क्या है? (What is the Section Formula?),को समझेंगे।
माना समतल में दो बिन्दु A और B हैं,यदि रेखाखण्ड AB पर कोई बिन्दु P,A व B के मध्य स्थित ह़ तो इस प्रकार के विभाजन को अन्त:विभाजन कहते हैं।यदि विभाजन बिन्दु P,A व B के मध्य में नहीं होकर A के बायीं या B के दायीं ओर स्थित हो तो ऐसे विभाजन को बाह्य विभाजन कहते हैं।
(1.)अन्त:विभाजन सूत्र (Internal Section Formula),आंतरिक रूप से किसी दिए गए अनुपात में एक पंक्ति रेखाखंड का विभाजन (Division of a line segment in a given ratio internally)-
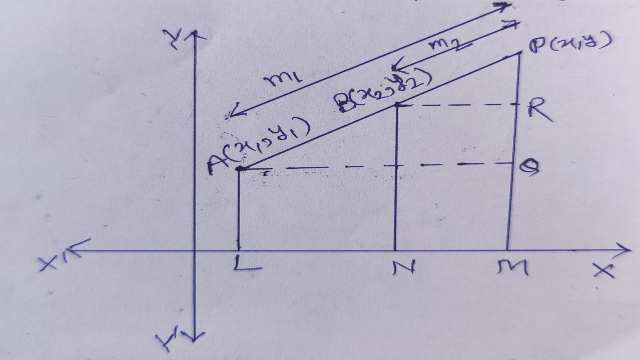
माना समतल में स्थित दो बिन्दु A\left(x_{1}, y_{1}\right) \text {और } B \left(x_{2}, y_{2}\right) हैं और बिन्दु और बिन्दु हैं और बिन्दु P(x,y) रेखाखण्ड AB को m_{1}:m_{2} में अन्त: विभाजित करता है।बिन्दु A,P और B से x-अक्ष पर डाले गए लम्ब AL,PM और BN हैं।बिन्दु A से PM पर लम्ब AQ और P से BN पर लम्ब PR डाला।तब
OL=x_{1},OM=x,ON=x_{2} \\ AL=y_{1}, PM=y \text { और } BN=y_{2} \\ AQ=L M=OM-OL=x-x_{1} \\ P R=MN=ON-O M=x_{2}-x \\ P Q=P M-Q M=P M-A L=y-y_{1} \\ BR=B N-R N=B N-P M=y_{2}-y
चित्र में त्रिभुज AQP और त्रिभुज PRB स्पष्टत: समरूप त्रिभुज हैं।
\frac{AP}{BP}=\frac{A Q}{P R}=\frac{P Q}{B R} \\ \frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x_{2}-x}=\frac{y-y_{1}}{y_{2}-y_{1}}
प्रथम दो अनुपात से-
\frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x_{2}-x} \\ \Rightarrow m_{1} x_{2}-m_{1} x=m_{2} x-m_{2} x_{1} \\ \Rightarrow\left(m_{1}+m_{2}\right) x=m_{1} x_{2}+m_{2} x_{1} \\ \Rightarrow x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}
पुनः प्रथम और अन्तिम अनुपात से
\frac{m_{1}}{m_{2}}=\frac{y-y_{1}}{y_{2}-y} \\ \Rightarrow m_{1} y_{2}-m_{1} y=m_{2} y-m_{2} y_{1} \\ \Rightarrow \left(m_{1}+m_{2}\right) y=m_{1} y_{2}+m_{2} y_{1} \\ \Rightarrow y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}
अतः P के अभीष्ट निर्देशांक
\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)
(2.)बाह्य विभाजन का विभाजन सूत्र (Section Formula for External Division),बाह्य रूप से विभाजन सूत्र (Externally Section Formula),बाह्य विभाजन के लिए सूत्र (Formula for External Division),बाह्य रूप से दिए गए अनुपात में एक पंक्ति रेखाखंड को कैसे विभाजित किया जाए? (How to divide a line segment in a given ratio externally)-
माना समतल में स्थित बिन्दु A\left(x_{1}, y_{1}\right) \text {और} B \left(x_{2}, y_{2}\right) हैं।बिन्दु P(x,y) रेखाखण्ड को m_{1}:m_{2} में बाह्य विभाजन करता है।बिन्दु A,B और P से x-अक्ष पर डाले गये लम्ब क्रमशः AL,BN और PM हैं।बिन्दु A से PM पर लम्ब AQ और B से PM पर लम्ब BR डाला।तब
OL=x_{1}, ON=x_{2}, OM=x,AN=y_{1},BN=y_{2} \text { और } PM=y \\ A Q=LM=OM-OL=x-x_{1} \\ BR=NM=OM-ON=x-x_{2} \\ PQ=PM-QM=P M-A L=y-y_{1} \\ \text { और } P R=PM-RM=PM-BN=y-y_{2}
चित्र में त्रिभुज AQP और त्रिभुज BRP स्पष्टत: समरूप त्रिभुज हैं।
\therefore \frac{A P}{B P}=\frac{A Q}{B R}=\frac{P Q}{P R} \\ \Rightarrow \frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x-x_{2}}=\frac{y-y_{1}}{y-y_{2}}
प्रथम दो अनुपात से-
\frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x-x_{2}} \\ \Rightarrow m_{1} x-m_{1} x_{2}=m_{2} x-m_{2} x_{1} \\ \Rightarrow\left(m_{1}-m_{2}\right) x=m_{1} x_{2}-m_{2} x_{1} \\ \Rightarrow x=\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}
पुनः प्रथम व अन्तिम अनुपात से-
\frac{m_{1}}{m_{2}}=\frac{y-y_{1}}{y-y_{2}} \\ \Rightarrow m_{1} y-m_{1} y_{2}=m_{2} y-m_{2} y_{1} \\ \Rightarrow \left(m_{1}-m_{2}\right) y=m_{1} y_{2}-m_{2} y_{1} \\ \Rightarrow y=\frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}
अतः P के अभीष्ट निर्देशांक
\left(\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}, \frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}\right)
विशेष स्थिति:यदि बिन्दु P रेखाखण्ड AB का मध्य बिन्दु हो अर्थात् P,AB को 1:1 में विभाजित करता हो तो P के निर्देशांक \left(\frac{x_{2}+x_{1}}{2}, \frac{y_{2}+y_{1}}{2}\right)
टिप्पणी:
(i)अन्त:विभाजन सूत्र से बाह्य विभाजन सूत्र विभाजन सूत्र प्राप्त करने के लिए m_{1} \text { या } m_{2} का चिन्ह ऋण कर देते हैं।
(ii)यदि बाह्य विभाजन में \left|m_{1}\right|>\left|m_{2}\right| हो तो विभाजन बिन्दु B के दायीं ओर (रेखा AB को B की ओर बढ़ाने पर) प्राप्त होता है।इसी प्रकार \left|m_{1}\right|<\left|m_{2}\right| हो तो विभाजन बिन्दु A के बायीं ओर (रेखा AB को A की ओर बढ़ाने पर) प्राप्त होता है।
(iii) यदि बिन्दु P(x,y) रेखाखण्ड AB को \lambda : 1 में विभाजित करता है तो P के निर्देशांक \left(\frac{x_{1}+\lambda x_{2}}{1+\lambda}, \frac{y_{1}+\lambda y_{2}}{1+\lambda}\right) होते हैं।\lambda को प्राचल मानते हुए बिन्दु \left(x_{1}, y_{1}\right) \text {व } \left(x_{2}, y_{2}\right) को मिलाने वाली रेखा पर किसी बिन्दु के निर्देशांक को उपर्युक्त रूप में व्यक्त कर सकते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Distance between two points
2.विभाजन सूत्र क्या है के उदाहरण (What is the Section Formula Examples)-
Example-1.उस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दु (3,5) और (7,9) को मिलाने वाले रेखाखण्ड को 2:3 के अनुपात में अन्त: विभाजित करता है।
Solution– माना बिन्दु A(3,5) व B(7,9) को बिन्दु C,2:3 के अनुपात में विभाजित करता है।माना C के निर्देशांक (x,y) हैं तो विभाजित सूत्र से
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow x=\frac{2 \times 7+3 \times 3}{2+3} \\ \Rightarrow x=\frac{14+9}{5} \\ \Rightarrow x=\frac{23}{5} \\ y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ \Rightarrow y=\frac{2 \times 9+3 \times 5}{2+3} \\ \Rightarrow y=\frac{18+15}{5} \\ \Rightarrow y=\frac{33}{5}
अतः विभाजन बिन्दु के निर्देशांक \left(\frac{23}{5}, \frac{33}{5}\right) होंगे।
Example-2. उस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (5,-2) और \left(-1 \frac{1}{2}, 4\right) को मिलाने वाले रेखाखण्ड को 7:9 को बाह्य विभाजित करता है।
Solution- माना बिन्दु A(5,-2) व B\left(-\frac{3}{2}, 4\right) को बिन्दु C(x,y) ,7:9 में विभाजित करता है। अतः बाह्य विभाजन सूत्र से-
x=\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}} \\ \Rightarrow x=\frac{7 \times \left(-\frac{3}{2}\right)-9 \times 5}{7-9} \\ \Rightarrow x=\frac{-\frac{21}{2}-45}{2} \\ \Rightarrow x=\frac{-21-90}{-2 \times 2} \\ \Rightarrow x=\frac{-11}{-4} \\ \Rightarrow x =27 \frac{3}{4} \\ y=\frac{m, y_{2}-m_{2} y_{1}}{m_{1}-m_{2}} \\ \Rightarrow y=\frac{7 \times 4-9 \times (-2)}{7-9} \\ \Rightarrow y=\frac{28+18}{-2} \\ \Rightarrow y=\frac{46}{-2} \\ \Rightarrow y=-23
अतः बिन्दु C के निर्देशांक \left(27 \frac{3}{4},-23\right) होंगे।
उपर्युक्त उदाहरण के द्वारा विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division) को समझ सकते हैं।
Example-3.सिद्ध कीजिए कि मूलबिन्दु O बिन्दुओं A(1,-3) और B(-3,9) को मिलाने वाले रेखाखण्ड को 1:3 के अनुपात में अन्त: विभाजित करता है।बाह्य विभाजन करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
Solution- माना बिन्दु O(0,0) बिन्दु A(1,-3) व B(-3,9) को m_{1}: m_{2} में विभाजित करता है। अतः विभाजन सूत्र से-
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow x= \frac{m_{1} \times (-3) +m_{2} \times 1}{m_{1}+m_{2}}=0(\text { दिया है}) \\ \Rightarrow -3 m_{1}+m_{2}=0 \\ \Rightarrow 3 m_{1}=m_{2} \\ \Rightarrow \frac{m_{1}}{m_{2}}=\frac{1}{3}\\ m_{1}: m_{2}=1:3
अतः बिन्दु O बिन्दु A व B को 1:3 में विभाजित करता है। पुनः माना बिन्दु C(x,y) ,बिन्दु A व B को 1:3 में बाह्य विभाजन करता है। अतः बाह्य विभाजन सूत्र से-
x=\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}} \\ \Rightarrow x=\frac{1 \times(-3)-3(1)}{1-3} \\ \Rightarrow x=\frac{-3-3}{-2} \\ \Rightarrow x=\frac{-6}{-2} \\ \Rightarrow x=3 \\ y=\frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}} \\ \Rightarrow y=\frac{1 \times 9-3 \times(-3)}{1-3} \\ \Rightarrow y=\frac{9+9}{-2} \\ \Rightarrow y=\frac{18}{-2} \\ \Rightarrow y=-9
अतः बाह्य विभाजन बिन्दु C(3,-9) है।
Example-4. बिन्दुओं (22,20) और (0,16) को मिलाने वाली रेखा के मध्य बिन्दु के निर्देशांक ज्ञात कीजिए।
Solution- माना A(22,20) व B(0,16) तथा मध्य बिन्दु (x,y) है तो
x=\frac{x_{1}+x_{2}}{2},y=\frac{y_{1}+y_{2}}{2} \\ \Rightarrow x=\frac{22+0}{2}, \quad y=\frac{20+16}{2} \\ \Rightarrow x=11, y=18
अतः मध्य बिन्दु के निर्देशांक (11,18) होंगे।
Example-5. बिन्दुओं (5,3) और (-3,-2) को मिलाने वाली रेखाखण्ड x-अक्ष द्वारा किस अनुपात में विभाजित होता है?
Solution- माना बिन्दु A(5,3) व B(-3,-2) x-अक्ष द्वारा m_{1}: m_{2} में विभाजित होता है अतः विभाजन सूत्र से-
y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}
[x-अक्ष पर y= 0 से]
\Rightarrow \frac{m_{1} (-2)+m_{2}(3)}{m_{1}+m_{2}}=0 \\ \Rightarrow-2 m_{1}+3m_{2}=0 \\ \Rightarrow 2 m_{1}=3 m_{2} \\ \Rightarrow m_{1}=m_{2}=3: 2
अतः x-अक्ष बिन्दु A व B को मिलाने वाले रेखाखण्ड को 3:2 में विभाजित करता है।
उपर्युक्त उदाहरण के द्वारा विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division) को समझ सकते हैं।
Example-6. बिन्दुओं (2,-3) और (5,6) को मिलाने वाली रेखाखण्ड y-अक्ष को किस अनुपात में विभाजित होता है?
Solution- माना बिन्दु A(2,-3) व बिन्दु B(5,6) y-अक्ष से m_{1}: m_{2} में विभाजित होता है। अतः विभाजन सूत्र से-
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}
[y-अक्ष पर x= 0 से]
\Rightarrow \frac{m_{1}(5)+m_{2}(2)}{2 m_{1}+m_{2}}=0 \\ \Rightarrow 5 m_{1}=-2 m_{2} \\ \frac{m_{1}}{m_{2}}=-\frac{2}{5}
अतः y-अक्ष AB से 2:5 में बाह्य विभाजित करता है।
Example-7. बिन्दुओं (15,5) और (9,20) मिलाने वाले रेखाखण्ड को बिन्दु (11,15) किस अनुपात में विभाजित करता है?
Solution– माना बिन्दु A(15,5) व B(9,20) को मिलानेवाले रेखाखण्ड को C(11,15) , m_{1}: m_{2} में विभाजित करता है। अतः विभाजन सूत्र से-
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow \frac{m_{1} \times (9)+m_{2} \times 15}{m_{1}+m_{2}}=11 \\ \Rightarrow 9 m_{1}+15 m_{2}=11 m_{1}+11 m_{2} \\ \Rightarrow 11 m_{1}-9 m_{1}=15 m_{2}-11 m_{2} \\ \Rightarrow 2 m_{1}=4 m_{2} \\ \Rightarrow m_{1}=2 m_{2} \\ \Rightarrow m_{1}=m_{2}=2: 1
अतः 2:1 में विभाजित करेगा।
उपर्युक्त उदाहरण के द्वारा विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division) को समझ सकते हैं।
Example-8. यदि बिन्दु P(3,5) बिन्दुओं A(-2,3) और B को मिलाने वाले रेखाखण्ड को 4:7 के अनुपात में अन्त: विभाजित करता है तो B के निर्देशांक ज्ञात कीजिए।
Solution- P(3,5) व A(-2,3)
माना है B \left(x_{2}, y_{2}\right) तो विभाजन सूत्र से-
x =\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow 3 =\frac{4\left(x_{2}\right)+7(-2)}{4+7} \\ \Rightarrow 4 x_{2}-14=33 \\ \Rightarrow 4 x_{2}=33+14 \\ \Rightarrow x_{2}=\frac{47}{4} \\ y= \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ \Rightarrow 5 =\frac{4\left(y_{2}\right) +7 \times 3}{4+7} \\ \Rightarrow 4 y_{2}+21=55 \\ \Rightarrow 4 y_{2}=55-21 \\ \Rightarrow y=\frac{34}{4} \\ \Rightarrow y_{2}=\frac{17}{2}
अतः बिन्दु B के निर्देशांक होंगे \left(\frac{47}{41}, \frac{17}{2}\right)
Example-9. बिन्दुओं (11,9) और (1,2) को मिलाने वाली रेखा को समत्रिभाजित करनेवाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
Solution– माना A(11,9) व B(1,2) को समत्रिभाजित करनेवाले बिन्दु C व D हैं।
C रेखाखण्ड AB को 1:2 में विभाजित करता है।
अतः विभाजन सूत्र से-
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow x =\frac{1 \times 1+2 \times 11}{1+2} \\ \Rightarrow x =\frac{1+22}{3} \\ x =\frac{23}{3} \\ y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ \Rightarrow y=\frac{1 \times 2+2 \times 9}{1+2} \\ \Rightarrow y=\frac{2+18}{3} \\ \Rightarrow y=\frac{20}{3}
अतः C के निर्देशांक \left(\frac{23}{3}, \frac{20}{3}\right) हैं।
पुनः D,AB को 2:1 में विभाजित करता है।
अतः विभाजन सूत्र से-
x=\frac{2 \times 1+1 \times 11}{2+1} \\ \Rightarrow x= \frac{2+11}{3} \\ \Rightarrow x=\frac{13}{3} \\ y=\frac{2 \times 2+1 \times 9}{1+2} \\ \Rightarrow y=\frac{4+3}{3} \\ \Rightarrow y=\frac{13}{3}
अतः D के निर्देशांक \left(\frac{13}{3}, \frac{13}{3}\right) हैं।
Example-10. बिन्दुओं (-4,0) और (0,6) को मिलाने वाले रेखाखण्ड को 4 बराबर भागों में बांटने वाले बिन्दुओं के निर्देशांक ज्ञात करो।
Solution- माना बिन्दु A(-4,0) व B(0,6) को मिलाने वाले रेखाखण्ड AB को बिन्दु C,D व E विभाजित करते हैं-
D बिन्दु AB का मध्य बिन्दु है अतः
\left(x=\frac{x_{1}+x_{2}}{2}, \quad y=\frac{y_{1}+y_{2}}{2}\right) \\ \Rightarrow D\left(\frac{-4+0}{2}, \frac{0+6}{2}\right) \\ \Rightarrow D\left(\frac{-4}{2}, \frac{6}{2}\right) \\ \Rightarrow D(-2,3)
पुनः C,AD का मध्य बिन्दु है। अतः
C\left(\frac{-4-2}{2}, \frac{0+3}{2}\right) \\ \Rightarrow C\left(-\frac{6}{2}, \frac{3}{2}\right) \\ \Rightarrow C(-3,\frac{3}{2})
पुनः E,DB का मध्य बिन्दु है। अतः
E\left(\frac{-2+0}{2}, \frac{3+6}{2}\right) \\ \Rightarrow E\left(-\frac{2}{21} ,\frac{9}{2}\right) \\ \Rightarrow E(-1,\frac{9}{2})
अतः विभाजन बिन्दु C(-3,\frac{3}{2}),D(-2,3) \text { और } E(-1,\frac{9}{2}) होंगे।
उपर्युक्त उदाहरण के द्वारा विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division) को समझ सकते हैं।
Example-11. ज्ञात कीजिए कि रेखा 3x+y=9 बिन्दुओं (1,3) और (2,7) को मिलाने वाले रेखाखण्ड को किस अनुपात में विभाजित करती है?
Solution- माना बिन्दु A(1,3) व बिन्दु B(2,7) को रेखा 3x+y=9 , m_{1} :m_{2} में विभाजित करती है। अतः विभाजन सूत्र से-
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow x=\frac{m_{1} \times (2)+m_{2} \times (1)}{m_{1}+m_{2}} \\ \Rightarrow x=\frac{2 m_{1}+m_{2}}{m_{1}+m_{2}} \\ y=\frac{m_{1} y_{2}+m_{2} y_{1}} {m_{1}+m_{2}} \\ \Rightarrow y=\frac{7 m_{1}+3 m_{2}}{m_{1}+m_{2}}
अतः x,y का मान समीकरण 3x+y=9 में रखने पर-
\Rightarrow 3\left[\frac{2 m_{1}+m_{2}}{m_{1}+ m_{2}}\right]+\frac{7 m_{1}+3 m_{2}}{m_{1}+m_{2}}=9 \\ \Rightarrow 6 m_{1}+3 m_{2}+7 m_{1}+3 m_{2}=9 m_{1}+9 m_{2} \\ \Rightarrow 13 m_{1}+6 m_{2}=9 m_{1}+9 m_{2} \\ \Rightarrow 13 m_{1}-9 m_{1}=9 m_{2}-6 m_{2} \\ \Rightarrow 4 m _{1}=3 m _{2} \\ \frac{m_{1}}{m_{2}}=\frac{3}{4} \\ \Rightarrow m_{1} :m_{2} =3:4
Example-12. वह अनुपात ज्ञात कीजिए जबकि बिन्दु (-3,p) बिन्दुओं (-5,-4) और (-2,3) को अन्त: विभाजित करता है।p का मान भी ज्ञात कीजिए।
Solution– माना C(-3,p) बिन्दु A(-5,-4) व B(-2,3) को m_{1} :m_{2} में विभाजित करता है। अतः विभाजन सूत्र से-
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ \Rightarrow x=\frac{m_{1}(-2)+m_{2}(-5)}{m_{1}+m_{2}}=-3 \\ \Rightarrow -2 m_{1}+5 m_{2}=-3 m_{1}-3 m_{2} \\ \Rightarrow-2 m_{1}+3 m_{1}=5 m_{2}-3 m_{2} \\ \Rightarrow m_{1}=2 m_{2} \\ \Rightarrow m_{1}:m_{2}=2:1 \\ \text { पुनः } \Rightarrow y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ \Rightarrow y=\frac{2(3)+1(-4)}{2+1} \\ \Rightarrow y=\frac{6-4}{3} \\ \Rightarrow y=\frac{2}{3} \\ \text { अतः } p=\frac{2}{3}
उपर्युक्त उदाहरणों के द्वारा विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division) को समझ सकते हैं।
3.विभाजन सूत्र क्या है की समस्याएं (What is the Section Formula Problems)-
(1.)उस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (-2,1) और (5,4) को मिलाने वाली रेखा को 2:3 के अनुपात में अन्त: विभाजित करता है।
(2.) उस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (-4,4) और (7,2) को मिलाने वाली रेखा को 4:7 के अनुपात में बाह्य विभाजित करता है।
(3.) x-अक्ष बिन्दुओं A(3,-5) और (-4,7) को को मिलाने वाली रेखा को किस अनुपात में विभाजित करती है?
(4.) बिन्दुओं (-3,5) और (4,-9) को मिलाने वाली रेखाखण्ड को बिन्दु (-2,3) किस अनुपात में विभाजित करता है?
(5.) यदि बिन्दु A(2,5) और B को मिलाने वाले रेखाखण्ड को बिन्दु P(-1,2);3:4 के अनुपात में अन्त: विभाजित करता है तो B के निर्देशांक ज्ञात कीजिए।
(6.) ज्ञात कीजिए कि रेखा x+y=4 बिन्दु (-1,1) और (5,7) को मिलाने वाली रेखा किस अनुपात में विभाजित करती है?
उत्तर (Answers):(1) \left(\frac{4}{5},\frac{11}{5}\right)
(2) \left(-18 \frac{2}{3}, 6 \frac{2}{3}\right)
(3.)5:7
(4.)1:6
(5.)(-5,-2)
(6.) 1:2
उपर्युक्त सवालों को हल करने पर विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division) को ठीक से समझ सकते हैं।
4.बाह्य विभाजन बिन्दु (External division point)-
एक अंतराल का बाहरी विभाजन
किसी दिए गए अनुपात में आंतरिक रूप से एक अंतराल AB को विभाजित करना A और B के बीच एक बिंदु पैदा करता है। बाहरी विभाजन अंतराल AB के बाहर एक बिंदु पैदा करता है। सामान्य तौर पर, मान लें कि P (x, y) AB पर है, लेकिन अंतराल AB और उस AP:PB = k:1 के लिए बाहरी है, कुछ k> 0 के लिए।
उपर्युक्त आर्टिकल में दिए गए विवरण के आधार पर विभाजन सूत्र क्या है? (What is the Section Formula?),दो बिन्दुओं के मध्य दूरी का अन्त: और बाह्य विभाजन (Internal and External Division of Distance Between two Points),अन्त: और बाह्य विभाजन क्या है? (What is internal and external division),विभाजन सूत्र कक्षा 10 (Section formula class 10) को भली-भांति समझ सकते हैं।
Also Read This Article:-Trigonometric Ratios of Special Angles
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
